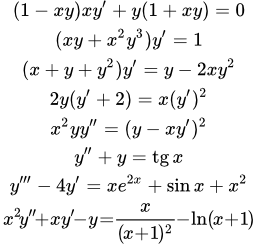Как решать дифференциальные уравнения второго порядка для чайников

Примеры дифференциальных уравнений с решениями

• Попробуйте решить приведенные ниже дифференциальные уравнения.
• Нажмите на изображение уравнения, и вы попадете на страницу с подробным решением.

Примеры решений дифференциальных уравнений первого порядка

Примеры решений дифференциальных уравнений второго и высших порядков

Найти общее решение дифференциального уравнения, или решение с заданными начальными условиями.

Примеры решений линейных дифференциальных уравнений с постоянными коэффициентами

Примеры решений линейных уравнений в частных производных первого порядка

Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .

Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность
, .

Автор: Олег Одинцов . Опубликовано: 28-01-2016 Изменено: 26-11-2021

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами

Основные понятия о линейных дифференциальных уравнениях второго порядка и их решениях

Линейным дифференциальным уравнением второго порядка называется уравнение вида

где y — функция, которую требуется найти, а p(x) , q(x) и f(x) — непрерывные функции на некотором интервале (a, b) .

Если правая часть уравнения равна нулю ( f(x) = 0 ), то уравнение называется линейным однородным уравнением. Таким уравнениям и будет в основном посвящена практическая часть этого урока. Если же правая часть уравнения не равна нулю ( f(x) ≠ 0 ), то уравнение называется линейным неоднородным уравнением (смотрите отдельный урок).

В задачах от нас требуется разрешить уравнение относительно y» :

Линейные дифференциальные уравнения второго порядка имеют единственное решение задачи Коши.

Линейное однородное дифференциальное уравнение второго порядка и его решение

Рассмотрим линейное однородное дифференциальное уравнение второго порядка:

Если y 1 (x) и y 2 (x) — частные решения этого уравнения, то верны следующие высказывания:

1) y 1 (x) + y 2 (x) — также является решением этого уравнения;

2) Cy 1 (x) , где C — произвольная постоянная (константа), также является решением этого уравнения.

Из этих двух высказываний следует, что функция

также является решением этого уравнения.

Возникает справедливый вопрос: не является ли это решение общим решением линейного однородного дифференциального уравнения второго порядка, то есть таким решением, в котором при различных значениях C 1 и C 2 можно получить все возможные решения уравнения?

Ответ на этот вопрос следуюший: может, но при некотором условии. Это условие о том, какими свойствами должны обладать частные решения y 1 (x) и y 2 (x) .

И это условие называется условием линейной независимости частных решений.

Теорема. Функция C 1 y 1 (x) + C 2 y 2 (x) является общим решением линейного однородного дифференциального уравнения второго порядка, если функции y 1 (x) и y 2 (x) линейно независимы.

Определение. Функции y 1 (x) и y 2 (x) называются линейно независимыми, если их отношение является константой, отличной от нуля:

Однако установить по определению, являются ли эти функции линейно независимыми, часто очень трудоёмко. Существует способ установления линейной независимости с помощью определителя Вронского W(x) :

.

Если определитель Вронского не равен нулю, то решения — линейно независимые. Если определитель Вронского равен нулю, то решения — линейно зависимымые.

Пример 1. Найти общее решение линейного однородного дифференциального уравнения .

Решение. Интегрируем дважды и, как легко заметить, чтобы разность второй производной функции и самой функции была равна нулю, решения должны быть связаны с экспонентой, производная которой равна ей самой. То есть частными решениями являются и .

Так как определитель Вронского

не равен нулю, то эти решения линейно независимы. Следовательно, общее решение данного уравнения можно записать в виде

.

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами: теория и практика

Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида

где p и q — постоянные величины.

На то, что это уравнение второго порядка, указывает наличие второй производной от искомой функции, а на его однородность — нуль в правой части. Постоянными коэффициентами называются уже упомянутые выше величины.

Чтобы решить линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами, нужно сначала решить так называемое характеристическое уравнение вида

которое, как видно, является обычным квадратным уравнением.

В зависимости от решения характеристического уравнения возможны три различных варианта решения линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами, которые сейчас разберём. Для полной определённости будем считать, что все частные решения прошли проверку определителем Вронского и он во всех случаях не равен нулю. Сомневающиеся, впрочем, могут проверить это самостоятельно.

Корни характеристического уравнения — действительные и различные

Иными словами, . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Пример 2. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет вид , его корни и — вещественные и различные. Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

.

Пример 3. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет вид , его корни и — вещественные и различные. Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

.

Корни характеристического уравения — вещественные и равные

То есть, . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Пример 4. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет равные корни . Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

Пример 5. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет равные корни . Соответствующие частные решения уравнения: и . Общее решение данного дифференциального уравения имеет вид

.

Корни характеристического уравнения — комплексные

То есть, , , . В этом случае решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами имеет вид

.

Пример 6. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет комплексные корни и . Соответственно и . Общее решение данного дифференциального уравения имеет вид

.

Пример 7. Решить линейное однородное дифференциальное уравнение

.

Решение. Характеристическое уравнение имеет комплексные корни и . Соответственно и . Общее решение данного дифференциального уравения имеет вид

.

Решить линейное однородное дифференциальное уравнение с постоянными коэффициентами самостоятельно, а затем посмотреть решение

Пример 8. Решить линейное однородное дифференциальное уравнение

.

Пример 9. Решить линейное однородное дифференциальное уравнение

.

Примеры решений задач по дифференциальным уравнениям

Теперь, когда вы научились находить производные и интегралы, самое время перейти к более сложной теме: решению дифференциальных уравнений (они же дифуры, диффуры и диф.уры :)), то есть уравнений, которые вместе с самой функцией (и/или аргументом), содержат и производную или даже несколько.

Как же решать дифференциальные уравнения? Главное, что понадобится, это а) умение правильно определить тип дифференциального уравнения и б) умение хорошо интегрировать — это существенная часть работы. А дальше следовать алгоримам для каждого из типов уравнений, которые подробно описаны в учебниках и ниже в примерах.

В этом разделе вы найдете решенные задачи на составление и решение дифференциальных уравнений. Примеры решений дифуров выложены бесплатно для вашего удобства и отсортированы по темам — изучайте, ищите похожие, решайте свои. Есть трудности в выполнении заданий? Мы готовы оказать помощь по дифференциальным уравнениям

Как решить дифференциальное уравнение онлайн?

Да ладно, неужели только вручную? Мучиться, определять тип, переносить, интегрировать, заменять, снова интегрировать, подставлять, выводить? Наверняка ведь есть онлайн-калькуляторы, которые позволяют решать дифференциальные уравнения?

У меня две новости, хорошая и плохая. Хорошая в том, что действительно самые распространенные типы дифференциальных уравнений математические программы умеют решать. Плохая в том, что обычно они выводят ответ (для научных расчетов этого достаточно), а не полное решение.

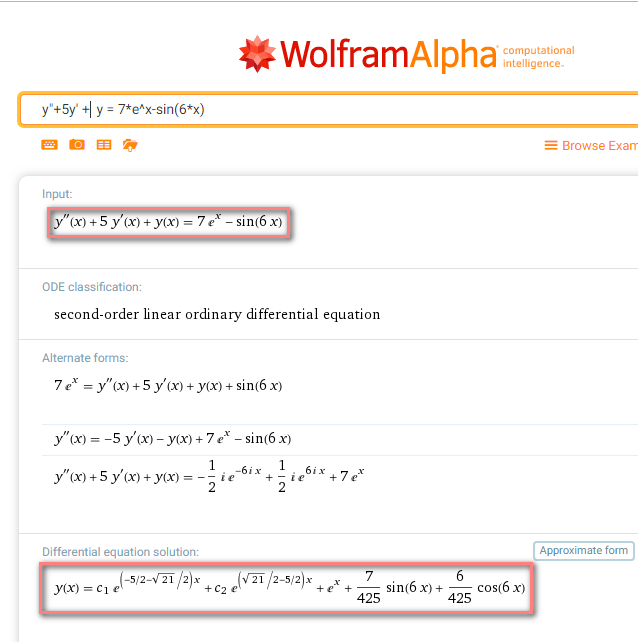
Есть известный математический сервис www.wolframalpha.com, которые представляет полные решения множества математических задач, в том числе диффуров онлайн (на английском языке) за 7 долларов в месяц. Ответы же доступны всем и могут помочь проверять правильность своего решения (см. ниже на скриншоте обведено само уравнение и его решение). Подробнее об этом сайте и типичных задачах, решаемых на нем, вы можете узнать тут.

Если вы забьете в поисковик что-то вроде «решить дифференциальное уравнение онлайн», то получите десятки ссылок на сайты, обещающие именно это.

Я проверила все сайты с первых страниц Яндекса и Гугла. Большая часть сайтов использует результаты расчетов www.wolframalpha.com (см. выше) и показывает вам ответ (и рекламу :)). Некоторые при этом не показывают даже ответа или говорят, что уравнение введено некорректно (хотя это вполне стандартное решаемое вручную линейное уравнение с постоянными коэффициентами). Полное решение не выдал ни один сайт.

Выводы? Бесплатно и полно и онлайн — не бывает. Хотите получать полные решения — используйте платную подписку на ВольфрамАльфа (или проконсультируйтесь у нас). Хотите ответы — там же бесплатно. Хотите научиться решать? Придется засучить рукава. Примеры на этой странице и ссылки внизу помогут вам. Удачи!

Общий интеграл, семейство кривых

Задача 1. Показать, что функция $y^2-x^2-Cy=0$ является общим интегралом дифференциального уравнения $y'(x^2+y^2)-2xy=0.$

Задача 2. Составить дифференциальное уравнение семейства кривых $C_1 x+(y-C_2)^2=0.$

Решения дифференциальных уравнений 1 порядка

Задача 3. Найти общее решение линейного дифференциального уравнения первого порядка $ xy’+x^2+xy-y=0.$

Задача 4. Решить однородное дифференциальное уравнение $y’=-y/x \quad (x \ne 0).$

Задача 5. Решить дифференциальное уравнение $(y^4-2x^3y)dx+(x^4-2xy^3)dy=0.$

Задача 6. Решить однородное дифференциальное уравнение $(2x+y+1)dx+(x+2y-1)dy=0.$

Задача 7. Решить линейное дифференциальное уравнение первого порядка $y’-2xy=3x^2-2x^4.$

Задача 8. Решить дифференциальное уравнение $(x+y^2)y’=y-1.$

Решение задачи Коши для ДУ

Задача 9. Решить дифференциальное уравнение с разделяющимися переменными $(1+x^2)dy-2xydx=0.$ Найти частное решение, удовлетворяющее начальному условию $y(0)=1$.

Задача 10. Решить задачу Коши для дифференциального уравнения второго порядка $2y y» +1 =(y’)^2, \, y(1/3)=1, \, y'(1/3)=2$.

Задача 11. Найти решение задачи Коши для дифференциального уравнения $$ y’= \frac<2y-x><2x+y>, y(1)=1. $$

Задача 12. Решить задачу Коши для дифференциального уравнения третьего порядка $$ y»’=x+\cos x, \quad y(0)=0, y'(0)=0, y»(0)=0. $$

Решения дифференциальных уравнений 2 порядка

Задача 13. Решить дифференциальное уравнение второго порядка с постоянными коэффициентами $y»+4y’+4y=xe^<2x>.$

Задача 14. Решить задачу Коши для дифференциального уравнения второго порядка с постоянными коэффициентами методом вариации: $$ y»-3y’=\frac<9e^<-3x>><3+e^<-3x>>, \quad y(0)=4\ln 4, y'(0)=3(3\ln 4-1). $$

Cоставление дифференциальных уравнений

Задача 15. Скорость остывания нагретого тела пропорциональна разности температур тела и окружающей среды. За 10 минут тело охладилось от 100 до 60 градусов. Температура среды постоянна и равна 20 градусам. Когда тело остынет до 25 градусов?

Задача 16. Моторная лодка движется в спокойной воде со скоростью 5 м/сек. На полном ходу ее мотор выключается и через 40 сек после этого скорость лодки уменьшается до 2 м/сек. Определить скорость лодки через 2 минуты после остановки мотора, считая, что сопротивление воды пропорционально скорости движения лодки.

Решения нелинейных дифференциальных уравнений

Задача 17. Решить дифференциальное уравнение $y^2 ^2 -2xyy’+2y^2-x^2=0.$

Задача 18. Решить дифференциальное уравнение $^2-4xyy’+8y^2=0.$