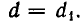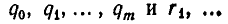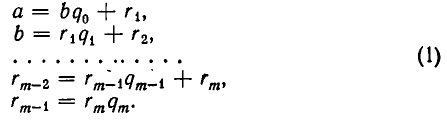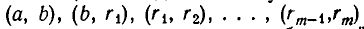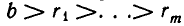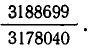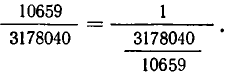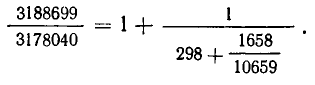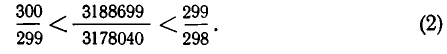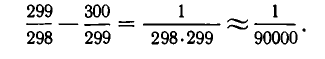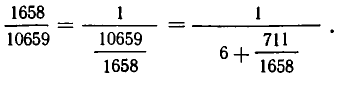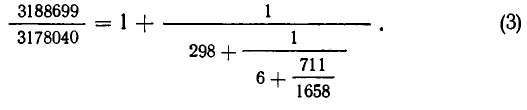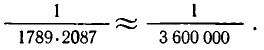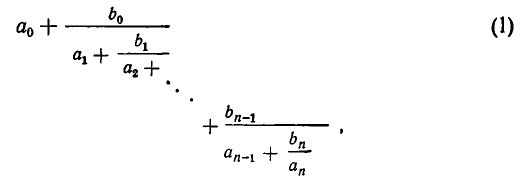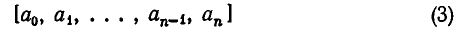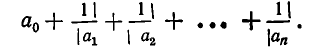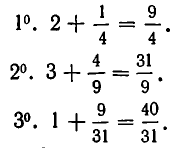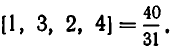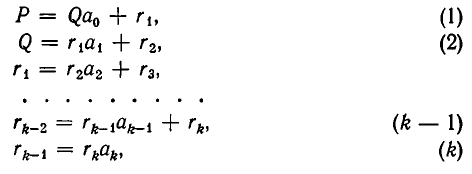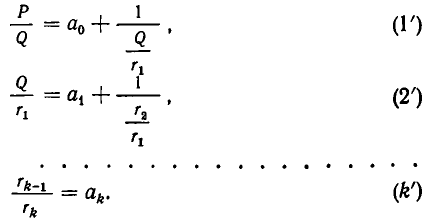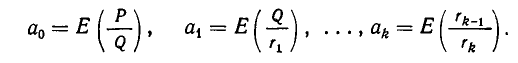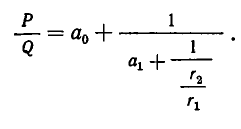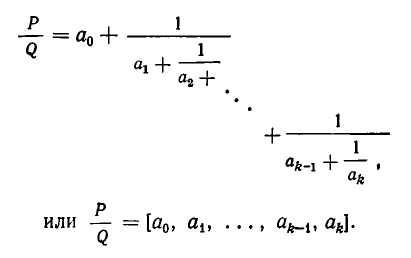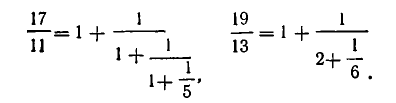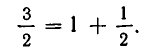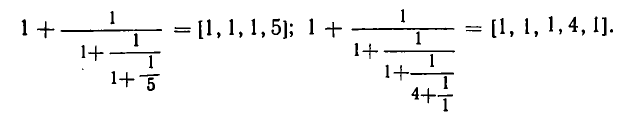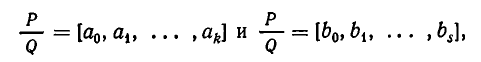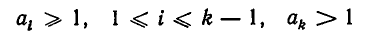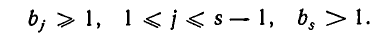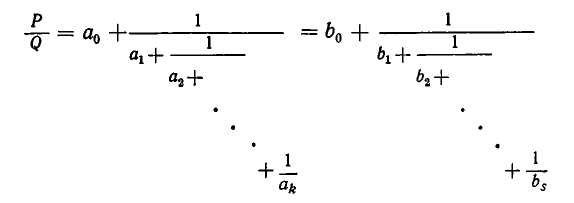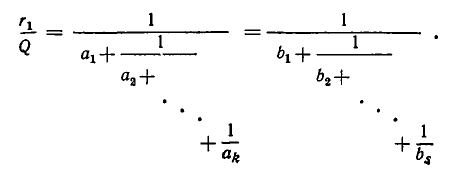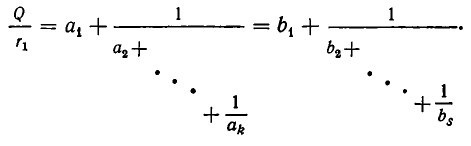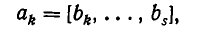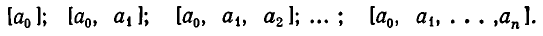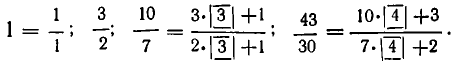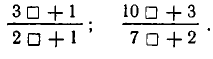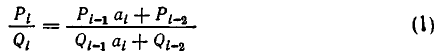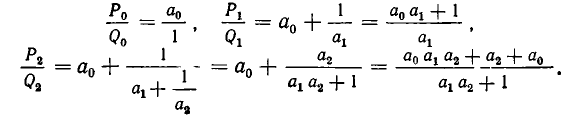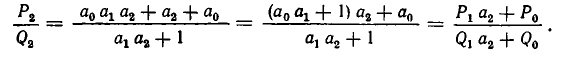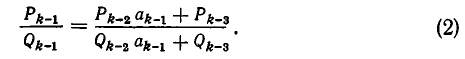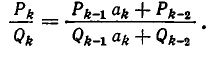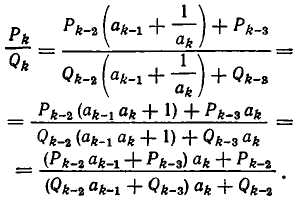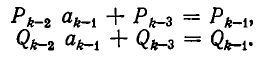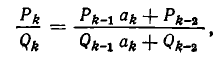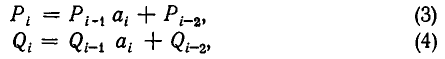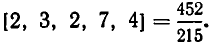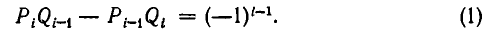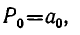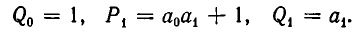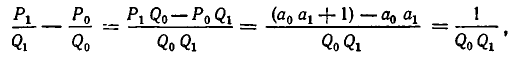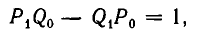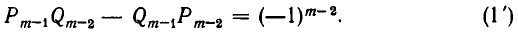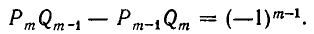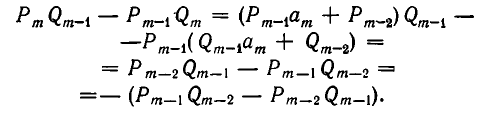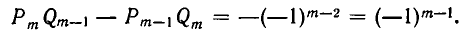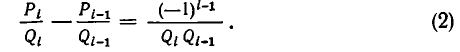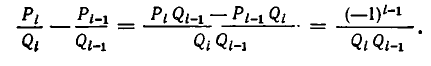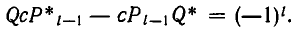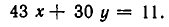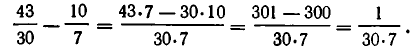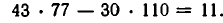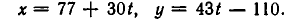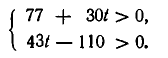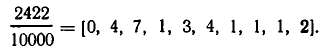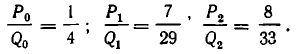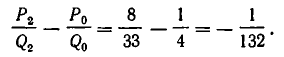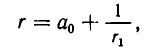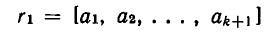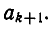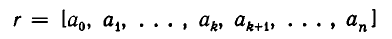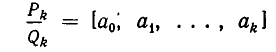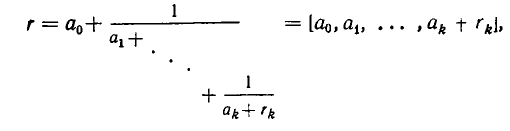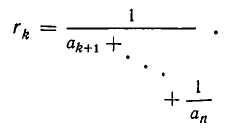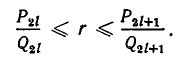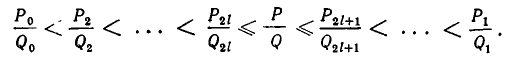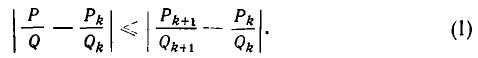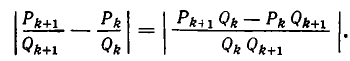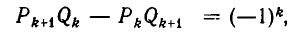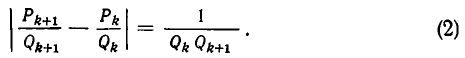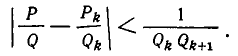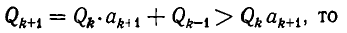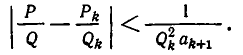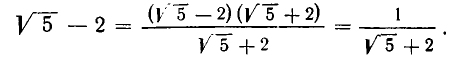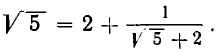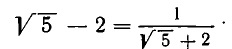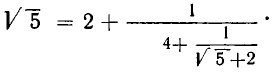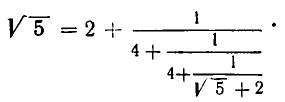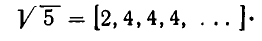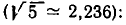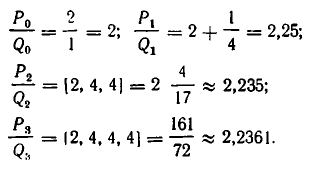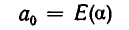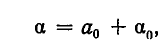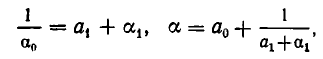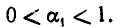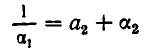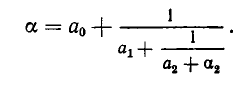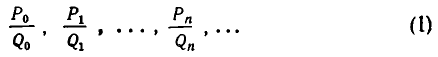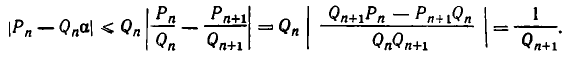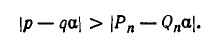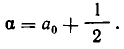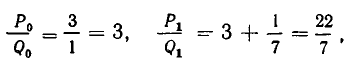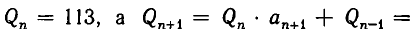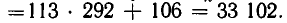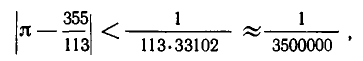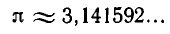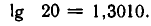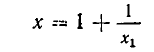Как решать диофантовы уравнения с помощью цепных дробей

Как решать диофантовы уравнения с помощью цепных дробей

Цепные дроби и диофантовы уравнения

Автор работы награжден дипломом победителя III степени

Актуальность исследования . Применение аппарата цепных дробей к прикладным задачам, в том числе олимпиадного характера, позволяет углубить математические знания, расширить кругозор и повысить мотивацию к изучению математики. Ведь задачи на оптимизацию, которых много в ЕГЭ, предполагают решение с помощью диофантовых уравнений; также в том пресловутом справочнике прозвучала мысль, что подход Диофанта к решению уравнений особенный, и мне хотелось бы поделиться умением решать диофантовы уравнения с другими. Я предполагаю, что элементы высшей математики могут быть доступны и интересны ученикам средней школы.

Объект исследования: цепные дроби и диофантовы уравнения.

Предмет исследования: применение последовательности подходящих дробей для решения диафантовых уравнений и других задач.

Обработка теоретического материала (его отбор, а также последовательное и доступное изложение);

Поиск областей применения цепных дробей;

Составление практического материала в форме упражнений.

Гипотеза исследования : применение цепных дробей позволяет найти один из способов решения диофантовых уравнений и других задач олимпиадного характера.

Изучить понятие цепных дробей и диофантовых уравнений;

На примерах приближения различных чисел подходящими дробями (рациональные числа, квадратичные иррациональности) понять закономерности использования аппарата цепных дробей;

Ознакомиться с историей возникновения и использования цепных дробей;

Выявить и применить возможности цепных дробей к решению разных видов олимпиадных задач.

Действительные числа однозначно отображаются цепными дробями. Основное значение такого изображения заключается в том, что, зная цепную дробь, изображающую действительное число, можно определить это число с достаточной точностью. Умение решать диофантовы уравнения может пригодиться в реальной жизни, например, задачи на оптимизацию, которые неоднократно встречаются в ЕГЭ; также данное умение окажется как нельзя кстати при решении задач, выходящих за рамки школьной программы, олимпиадных заданий.

Глава 1. Понятие цепных дробей.

Примеры разложений действительных чисел в цепную дробь.

Дробь можно записать в виде суммы целой части и правильной дроби: . Но , а дальше: . Значит, . Далее получим .

Продолжим этот процесс до тех пор, пока не придем к знаменателю . В результате мы представим обыкновенную дробь в виде:

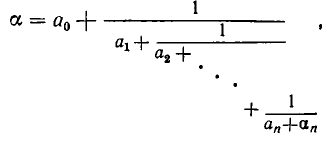
Эйлер назвал дроби такого вида непрерывными. Приблизительно в то же время в Германии появился другой термин – цепная дробь. Так за этими дробями и сохранились оба названия. Ввиду громоздкости развернутой записи цепной дроби применяют компактную запись .

В качестве примера представим дробь в виде цепной дроби:.

Или в компактной форме: [1; 3, 2, 4 ].

Мы познакомились с разложением в цепную дробь обыкновенной дроби, т.е. рационального числа. Любое рациональное число представимо в виде конечной цепной дроби. Конечность следует из алгоритма Евклида. Но в виде цепной дроби можно записать любое действительное число. Только конечными цепными дробями здесь не обойтись. Приведем разложение в непрерывную дробь числа .

и т.д. Видна закономерность.

Т.е. в компактной форме = [1: 2, 2, 2, 2, 2…].

Оказывается, квадратичные иррациональности (т.е. числа вида , где a , b , c — рациональные числа), и только они раскладываются в бесконечные периодические дроби. На этот факт впервые указал Эйлер, строгое его доказательство дал Лагранж.

Если оборвать дробь на знаменателе , то останется дробь . Обращая ее в обыкновенную, получим . Это выражение называют k —й подходящей дробью для исходной цепной дроби.

Например, для нашей дроби имеем:

нулевая подходящая дробь: ,

первая подходящая дробь: ,

вторая подходящая дробь: ,

третья подходящая дробь: . Она равна самому числу.

Для цепной дроби, представляющей число, имеем следующие подходящие дроби:

нулевая подходящая дробь: ,

первая подходящая дробь: ,

вторая подходящая дробь: ,

третья подходящая дробь: и т.д.

Подходящие дроби удобно вычислять с помощью специальной таблицы. Для этого посмотрим, как вычисляются подходящие дроби:

и т.д. Вообще имеют место рекуррентные соотношения

Эти вычисления удобно производить последующей схеме:

В первой строке этой таблицы записаны недробные элементы, с которых мы начинали строить каждый «этаж», нашей многоэтажной дроби.

Во второй строке сначала записано число 1. Это ключевое число, и надо просто запомнить, что вторая строка начинается с числа 1. Далее записаны числители подходящих дробей.

В третьей строке сначала записано число 0. Это ключевое число, и надо просто запомнить, что третья строка всегда начинается с числа 0.Далее записаны знаменатели подходящих дробей.

Оказывается, что, зная лишь нулевую подходящую дробь, следуя нашим рекуррентным соотношениям, можно найти сколь угодно много числителей и знаменателей в подходящих дробях.

Для получения очередного числителя (знаменателя) необходимо взять элемент того же столбца из первой строки умножить на предыдущий числитель (знаменатель) и прибавить к произведению «предпредыдущий» числитель (знаменатель).

Составим таблицу подходящих дробей для цепной дроби, изображающей число.

При этом, если учесть, что , , , =1,41666, то можно увидеть, что чем дальше мы идем, тем лучшее приближение числа получаем.

Цепные дроби обладают следующим важным свойством: если действительное число x записать в виде непрерывной дроби, то подходящая дробь дает наилучшее приближение числа x среди всех дробей, знаменатели которых не превосходят . Т.е. чем больше k , тем k – подходящая дробь ближе к числу.

В связи с этим замечательным свойством рассмотрим применение цепных дробей в календаре.

Глава 2. Приложения цепных дробей

Календарь и подходящие дроби

Древнеримские жрецы, ведавшие исчислением времени, произвольно удлиняли некоторые года, чтобы согласовать календарные даты с сезонными явлениями природы. Впервые порядок в счете времени навел в I в. до нашей эры римский император Юлий Цезарь. Он постановил считать одни годы по 365 суток, а другие по 366 суток, чередуя их по правилу три года подряд коротких, четвертый – длинный. Гораздо позже, с введением христианского летоисчисления, високосным стали считать каждый год, порядковый номер которого делится на 4. Этот календарь в честь Юлия Цезаря называется юлианским. По нему продолжительность суток составляет 365 суток 6 ч, что больше истинной лишь на 11 мин 14 с. Однако и это решение оказалось неудовлетворительным. К XVI в. ошибка, накапливаясь, составила уже около 10 суток.

Следующую реформу календаря провел Григорий XIII – папа римский. Было решено: сдвинуть числа на 10 дней, оставить чередование простых и високосных лет, при этом, если порядковый номер года оканчивается двумя нулями, но число сотен не делится на 4, то этот год простой. В настоящее время расхождение между юлианским и новым, григорианским календарями составляет 13 дней, поскольку с тех пор накопилось еще три дня (в 1700, 1800 и 1900 гг.). Продолжительность григорианского года составляет

365, 2425 суток, т.е. 365 суток 5 ч 49 мин 12 с, т.е. она больше истинной лишь на 26с. Полученная точность очень велика и вполне достаточна для практических нужд.

Интересная система календаря была предложена среднеазиатским математиком и поэтом Омаром Хайямом (ок.1048-1122), по ней високосными годами должны были считаться 8 лет из каждых 33. Продолжительность года по О. Хайяму составляет 365 суток, его погрешность всего 19с в год.

В 1864 г. русский астроном И. Медлер предложил с XX столетия ввести в России следующую поправку к юлианскому календарю: через каждые 128 лет пропускать один високосный год из 32, которые выпадают на этот период. Этот календарь самый точный из всех перечисленных. Здесь погрешность сокращается всего до 1с. Однако календарь И. Медлера не был принят, видимо, из-за того, что период в 128 лет не является «круглым» числом.

Системы календаря оказываются связанными с записью астрономического года в виде цепной дроби:

Год продолжительностью 365 суток — это нулевая подходящая дробь этой цепной дроби, 365 — юлианский год – первая подходящая дробь, 365, 365 и 365 — вторая, третья и четвертая подходящие дроби. А именно:

Системой, соответствующей второй подходящей дроби: семь високосных лет из 29, никто не предложил воспользоваться, видимо, потому, что третья подходящая дробь ненамного сложнее, а точность ее гораздо больше (вспомним, что это система О. Хайяма), а четвертой подходящей дроби соответствует система И. Медлера.

Второе свойство цепных дробей

Вспомним, как вычисляются подходящие дроби.

и т.д. Имеют место рекуррентные соотношения

Второе свойство цепных дробей: для любого k = 1,2,…, n имеет место формула

Диофантовы уравнения вида ax+ by =с с использованием цепных дробей.

Используем отмеченное нами свойство цепных дробей для решения уравнения ax+ by = c Коэффициенты a и b взаимно просты. Разложим в цепную дробь. При этом .

Поскольку обе дроби несократимы, то a = P _n , b = Qn . По свойству имеем

Умножив обе части этого равенства на (-1) n c , получим

Общее решение запишется в виде:

Решим уравнение 17х + 13у = 5.

Поскольку , то n = 2, ,откуда х₀ = -5•3 = -15, у₀= 4•5 = 20 и общее решение имеет вид

При решении уравнений вида ax + by = c будем использовать следующий алгоритм :

1) Разложим в цепную дробь (с помощью алгоритма Евклида или с помощью соответствующих преобразований).

2) Из разложения =определяем значение n (т.е. длину цепной дроби).

3) Находим n -1 – подходящую дробь (в случае необходимости используем таблицу).

4) Применяем формулы:

1) Можно находить сначала частное решение:

Глава 3. Диофантовы уравнения

Диофантовыми уравнениями называются алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неизвестных в уравнениях должно быть не менее двух. Диофантовы уравнения имею, как правило, много решений, поэтому их называют неопределенными уравнениями. К диофантовым уравнениям приводят задач, по смыслу которых неизвестные значения величин могут быть только целыми числами. В качестве примера задача на составления диофантовых уравнений, может служить задача о размере рубля монетами достоинством в 1; 2; 3; 5; 10; 15 и 50 копеек. Соответствующее уравнение имеет вид:

Решить такое уравнение – это значит найти все такие наборы.

Число наборов, удовлетворяющих этому уравнению примерно равно

510 * 10 7 . Названы эти уравнения по имени греческого математика. Его книга «Арифметика» содержала большое количество интересных задач, его изучали математики всех поколений. Книга сохранилась до наших дней, её можно найти в русском переводе в библиотеке. К диофантовым уравнениям приводят задачи, по смыслу которых неизвестные значения величин могут быть только целыми числами.

Для линейных уравнений с двумя неизвестными, т.е. уравнение вида

ax + by = c , где a , b , c – целые числа, а x , y – целочисленные решения уравнения. для данного уравнения справедливы следующие утверждения:

Если коэффициенты a и b уравнения ax + by = c являются взаимно простыми числами (их наибольший общий делитель d =1), то это уравнение имеет, по крайней мере, одно целочисленное решение.

Если d ≠1, то уравнение ax + by = c не имеет целочисленных решений.

Если d =1/ то уравнение ax + by = c имеет бесконечное множество целочисленных решений, которые задаются формулами х = α + bt , y = β – at ,

Где ( α ; β ) – некоторое целочисленное решении уравнения ax + by = c , at t – произвольное целое число.

Долгое время надеялись отыскать общий решения любого диофантова уравнения. Однако в 1970 году ленинградский математик Ю.В. Матиясевич доказал, что такого общего способа быть не может.

Рассмотрим решение системы диофантовых уравнений первой степени на конкретном примере:

Решить в целых числах систему уравнений:

Решение: вычтем из второго уравнения первое, получим yz — y — z =5

или ( y -1)( z -1)=6. Число 6 можно разложить на целые множители четырьмя способами:

Эти системы дают тройки значений

( x ; y ; z ): (5;2;7), (5;7;2), (7;4;3), (7;3;4), (19;-5;0), (17;-2;-1), (17; -1;-2).

Диофантовы уравнения решаются методом перебора (один из самых древнейших методов решения математических задач, возникающих на практике).

А также нужно помнить, что если число d есть наибольший делитель целых чисел a и b , то существует такие числа k и 1, что d = ka + lb . Алгоритм Евклида позволяет вычислить целые числа k и 1.

Линейное диофантово уравнение ax + by = c не будет иметь решений, если числа с и d взаимно простые. Если число с кратно числу d , то одно из решений уравнения будет иметь вид: x = pk и y = pl .

Если целое число c делится на D ( a ; b ), то уравнение ax + by = c имеет целые решения (если некоторые из чисел a , b и с отрицательны, то вместо них берем их модули).

Рассмотрим, как искать эти решения на следующем примере:

Это уравнение может иметь целые решения, так как D (28;40)=4, а число 60 делится на цело, на 4. Ясно, что любое целое решение уравнения 28 x – 40 y =60 удовлетворяют и уравнению 7 x – 10 y = 15 из заданного сокращения обеих частей на 4. Обратно любое целое решение уравнения 7 x – 10 y = 15, является и целым решением заданного уравнения. У получившегося после сокращения на 4 уравнение 7 x – 10 y = 15 коэффициенты при неизвестных взаимно просты, т.е. D (7;10) равно 1.

Применим к этим коэффициентам алгоритм Евклида. Мы видим, что при делении числа 7 на 3 получилось неполное частное 2 и остаток 1, а потому 7 = 2*3 + 1. Значит 1=7-2*3. таким же путем устанавливаем, что 10=1*7+3, а потому 3=10-1*7. Подставляя это выражение в равенство 1=7-2*3, получаем 1=7-2(10-1*7). Раскрывая скобки, получаем x =3 и y =2 дают целые решения уравнения 7 x – 10 y = 15. Чтобы получить целые решения уравнения 7 x – 10 y = 15, надо оба этих числа умножить на 15. Таким путем мы получим одно решение уравнения

Другие целые решения того же уравнения имеют вид: х=45+10 t , y =30 + 7 t , где t – любое число.

Чтобы выделить целые неотрицательные решения заданного уравнения, надо найти такие значения t , при которых 45 +10 t >0 и 30+7 t >0. Из этих неравенств находим, что должны выполняться условия t >-4,5, t >-30/7, из которых вытекает, что t >-4.

Итак, данное уравнение имеет бесконечно много целых неотрицательных решений, задаваемых формулами х=45+10 t , y =30 + 7 t , где t принимает значение -4, -3,-2, …

Часть 4. Применение теории на практике

x^2 + y^2 – 2x + 4y=-5

В левой части уравнения выделим полный квадрат:

x^2 – 2x + 1 + y^2 + 4y + 4=0

Сумма квадратов равна 0 лишь в одном случае

Решив систему, получим, что x= 1, y= -2

x^2 – 6x + y^2 + 6y + 18=0

Докажем, что это уравнение имеет единственное целочисленное решение.

В левой части уравнения выделим полные квадраты :

( x – 3 )^2 + ( y + 3 )^2=0

Данное уравнение имеет решение, когда

Теперь я предлагаю рассмотреть графический метод решения диофантовых уравнений.

Алгоритм построения графика уравнения ах + by + с = 0:

1. Придать переменной х конкретное значение х= х1; найти из уравнения ах1 + by + c = 0 соответствующее значение y =y1.

2. Придать переменной х другое значение х=х2; найти из уравнения ах2 + by + c = 0 соответствующее значение y =y2.

3. Построить на координатной плоскости х Oy две точки (х1;у1) и (х2;у2).

4. Провести через эти две точки прямую – она и будет графиком уравнения ах + by + с = 0.

Необходимо найти все пары (х, у) целых чисел, удовлетворяющих системе неравенств:

Рассмотрим на координатной плоскости области, которые описываются заданными неравенствами. А затем выберем в них лишь точки с целочисленных координат х, у.

Получаем два случая:

1) Неравенство (1) путем выделения полных квадратов сводится к условию

2) Неравенство (2) сводится к виду

Единственной точкой, принадлежащей одновременно двум кругам, будет точка М( 12; -8). Это выясняется подстановкой в систему числовых значений координат всех узлов квадратной сетки, соседних с точкой М.

Пример 1. Для перевозки большого количества контейнеров по 170 кг и по 190 кг выделены трехтонные машины. Можно ли ими загружать машины полностью?
Решение. пусть х и у количество контейнеров по 170 и 190 кг соответственно, тогда имеем уравнение

Для нахождения частного решения воспользуемся разложением дроби в цепную дробь

Свернув предпоследнюю подходящую к ней дробь в обыкновенную

Частное решение данного уравнения имеет вид:

х ₀ = (-1) 4 300∙9=2700, у ₀ =(-1) 5 300∙8= -2400,
а общее задается формулой х=2700 — 19k, y= — 2400 + 17k.
откуда получаем условие на параметр k: 141 ≤ k ≤ k=142, x=2, y=14.

Пример 2. Разложить в цепную дробь .

Решение. Находим: a0=1, . Поскольку , будем иметь a1=a0=1, так что и так далее, то есть

Задания для самостоятельного решения

Пример 1. Найти значение следующих цепных дробей:

Пример 2. Найти значение цепной дроби .

Пример 3. Решить в целых числах уравнение 54х + 37у = 1.

Подведем итоги. В ходе исследования была проведена следующая работа:

1)Собран и освоен теоретический материал, составлены на основании изученных свойств алгоритм решения приведенных в данной работе диофантовых уравнений. Сформулированы замечания, использующиеся при решении данных уравнений.

2)Найдены некоторые области применения цепных дробей.

3)Составлены и выполнены практические задания по разложению действительных чисел в цепные дроби, а также по решению диофантовых уравнений вида ax + by = c , других олимпиадных задач.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

Баврин И.И.,Фрибус Е.А. Занимательные задачи по математике.- М.: Гуманитарный издательский центр ВЛАДОС, 1999.- 208 с.

Басова Л.А., Шубин М.А., Эпштейн Л.А. Лекции и задачи по математике.- М.: Просвещение, 1981.- 96 с.

Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия: Книга для учащихся 10-11 кл. общеобразовательных учреждений.- М.: Просвещение, 1996.- 320 с.

Ожигова Е. П. Что такое теория чисел.- М.: Знание, 1970.- 96 с.

Пичурин Л. Ф. За страницами учебника алгебры: Книга для учащихся 7-9 кл.сред.шк.- М.: Просвещение, 1990.- 224 с.

Савин А. П. Энциклопедический словарь юного математика.- М.: Педагогика, 1989.- 352 с.

Хинчин А. Я. Цепные дроби.- М.: Наука, 1978.- 112 с.

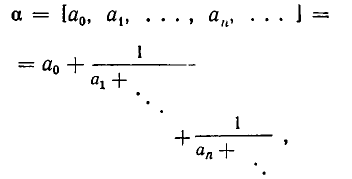
Непрерывная дробь (цепная дробь) в математике с примерами решения и образцами выполнения

Непрерывная дробь (или цепная дробь) — это конечное или бесконечное математическое выражение вида. где. есть целое число, а все остальные. — натуральные числа (положительные целые). При этом числа. называются неполными частными или элементами цепной дроби.

Конечные цепные дроби

В арифметике часто приходится искать наибольший общий делитель двух натуральных чисел. В младших классах эту задачу решают с помощью разложения чисел на прос­тые множители. Однако этот способ в школе не получает теорети­ческого обоснования, так как он опирается на не доказываемую (а часто и не формулируемую ) довольно трудную теорему о суще­ствовании и единственности разложения натуральных чисел на простые множители.

Другой метод решения этой задачи, свободный от указанного недостатка, изложен еще в книге Евклида «Начала» (III век до н. э.); его называют алгоритмом Евклида или способом последовательного деления. Изложим этот способ.

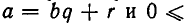
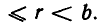
Напомним сначала некоторые свойства деления с остатком. Пусть а — целое число и b — натуральное число. Существуют та­кие целые числа q (частное) и r (остаток), что Эти числа однозначно определены.

Справедливо следующее утверждение: если а = bq + r, то наибольший общий делитель чисел а и b совпадает с наибольшим общим делителем чисел b и r.

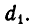
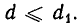
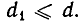
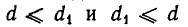
В самом деле, обозначим наибольший общий делитель чисел а и b через d, а наибольший общий делитель чисел b и r — через Из соотношения r = а — bq получаем, что d является делителем и числа r, то есть d будет общим (но не обязательно наиболь­шим) делителем чисел b и r. Отсюда следует, что Обратно, из соотношения а = bq + r следует, что наибольший общий дели­тель чисел b и r является делителем числа а, а значит, Из двух соотношений получаем

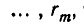
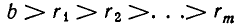
Теперь опишем алгоритм Евклида. Он заключается в том, что для целого числа а и натурального числа b последовательно находят две конечные последовательности чисел такие, что и

Тогда 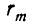— наибольший общий делитель чисел а и b. Это следует из того, что по доказанному наибольшие общие делители пар чисел

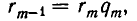
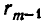
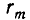
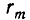
совпадают друг с другом. Но и потому наибольший общий делитель чисел и равен .

Заметим, что цепь равенств (1), выражающая алгоритм Евкли­да, не может быть бесконечной, так как из

вы­текает, что в (1) не более чем b равенств.

Пример цепной дроби

В некоторых приложениях математики встречаются очень громоздкие дроби. Возникает вопрос, нельзя ли подобрать дробь со сравнительно небольшим знаменателем, дос­таточно близкую к данной громоздкой дроби. Аппаратом для реше­ния этой задачи являются дроби особого вида, называемые цепны­ми или непрерывными дробями.

Прежде чем излагать общую теорию цепных дробей, рассмотрим следующий пример. Отношение экваториального радиуса Земли к ее полярному радиусу выражается дробью

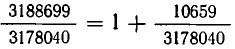
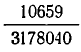
Попробуем упростить эту дробь. Для этого сначала выделим из нее целую часть: . Оставшуюся дробную часть преобразуем так:

В знаменателе получившейся дроби снова выделим целую часть:

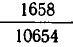
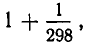
Это выражение позволяет получить хорошее приближение для рассматриваемой дроби. Ясно, что при отбрасывании в знаменателе дробной части мы получим число которое

больше, чем наша дробь. Если же округлить знаменатель в сторону увеличения, то мы получим дробь 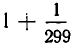, которая меньше рассматриваемой. Таким образом,

Разность полученных приближений 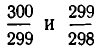мала:

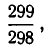
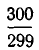
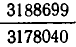
Значит, как так и дают приближенное значение для дроби с точностью не меньшей, чем

Если мы хотим получить еще лучшее приближение, надо аналогичным образом преобразовать отброшенную дробную часть

Подставляя это выражение в (1), получаем:

Ясно, что дробь 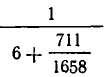заключена между

Поэтому получаем для границы:

или, преобразуя дроби,

Получились оценки с большими знаменателями, чем в (2). Но их точность существенно выше — погрешность полученных приближений не больше, чем

Продолжая описанный процесс, мы получим в конце концов точное выражение для 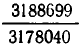в виде «многоэтажной» дроби:

Разумеется, полученная дробь менее удобна, чем . Но она позволяет получать приближенные значения заданной дроби, имеющие небольшие знаменатели. Чтобы получить такие приближенные значения, надо оборвать процесс на каком-то шагу, заме­нив смешанное число его целой частью, и превратить полученное выражение в обыкновенную дробь. Дроби вида (4) и называют цепными или, иначе, непрерывными дробями.

Определение цепной дроби

Введем следующее общее определение:

Всякое выражение вида

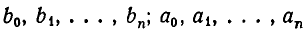
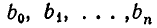
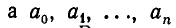
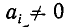
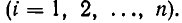
где могут быть любыми действительными или комплексными числами, а также функциями от одной или нескольких переменных, называется конечной цепной (или непре­рывной) дробью. называются частными числителя­ми, — частными знаменателями или неполными частными. В записи (1), естественно, предполагается, что Это условие не касается а0, которое может быть равным нулю.

Для получения приближенных значений дробей используют частный вид цепных дробей, у которых все числители равны 1 а знаменатели — натуральные числа

Форма записи (2), как и форма (1), очень громоздка; поэтому вместо (2) часто употребляются упрощенные записи, например

Все же часто мы будем пользоваться развернутой записью (2).

Ясно, что всякая цепная дробь вида (2) выражает некоторое рациональное число. Чтобы получить выражение этого числа в виде обыкновенной дроби, надо «свернуть» цепную дробь, выполняя (начиная «с конца») все указанные операции.

Пример:

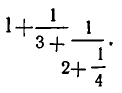
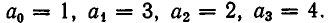
Вычислить значение цепной дроби Здесь Вычисление будет состоять из следующих шагов:

Ответ:

Обращение конечной цепной дроби в обыкновенную — всегда выполнимая задача. На это потребуется не более чем n шагов, каждый из которых состоит в сложении двух чисел: целого числа и правильной дроби.

Представление рациональных чисел в виде конечной цепной дроби

В предыдущем параграфе было показано, что любую конеч­ную цепную дробь можно обратить в рациональное число. Пока­жем теперь, что и обратно — любое рациональное число r можно обратить в цепную дробь.

Теорема:

Всякое рациональное число можно представить в виде конечной цепной дроби.

Доказательство:

Всякое рациональное число r можно представить в виде отношения двух целых чисел 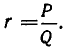При этом, не теряя общности, можно считать (в противном случае изменим знаки у Р и Q). Применим к числам Р и Q алгоритм Евк­лида (см. § 1):

где (если то Каждое из полученных равенств можно переписать по-другому:

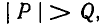
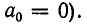
Нетрудно заметить, что каждое из этих равенств можно понимать как нахождение целой части неправильной дроби; каждое из неполных частных 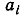представляет собой целую часть соответствующей дроби:

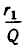
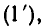
Подставив значение дроби из (2′) в знаменатель дроби равенства получим:

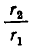
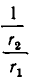
Затем значение дроби , взятое из равенства (3), подставим в знаменатель дроби . Продолжая процесс подстановки до конца, получим:

Число частных знаменателей, которое получится при разложении заданного рационального числа в цепную дробь, заранее узнать невозможно. Оно зависит от «природы» числа. Так, мало отличающиеся «на вид» числa .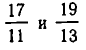

разлагаются в цепные Дроби, имеющие разное число частных знамена­телей:

Обратите внимание на характер доказательства теоремы 1. По существу получено больше, чем требовалось. Ведь надо было лишь доказать, что любое рациональное число можно представить в виде конечной цепной дроби. Мы же не только доказали этот факт, но и указали способ построения искомой цепной дроби.

Покажем теперь, что разложение любого рационального числа в цепную дробь однозначно определено. При этом рассматриваются лишь разложения, удовлетворяющие следующему условию: последний частный знаменатель должен быть больше 1. В противном случае могут существовать и различные разложения в цепную дробь одного и того же рационального числа.

Пример:

Разложим в цепную дробь число

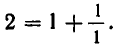
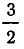
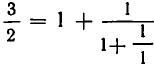
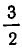
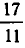
Последний частный знаменатель можно представить в виде В таком случае число можно записать в виде цепной дроби по-иному: . Получилось, что одну и ту же дробь мы разложили в цепную дробь двумя различными способами: [1, 2] и [1, 1, 1]. Так можно поступить с любым ра­циональным числом. Например, для числа можно получить две цепные дроби:

Чтобы исключить двузначность в разложении рационального числа в цепную дробь, связанную с такими искусственными «удлинениями», как раз и приходится предполагать последний частный зна­менатель большим 1.

Однозначность разложения мы докажем от противного. Допустим, что число удалось разложить в две разные цепные дроби:

При этом допускается, что различны не только сами частные знаменатели, но и их количество .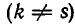

Мы имеем равенства:

Так как — натуральные числа, то лежит между 0 и 1, Иными словами, . Точно так же . Значит, и

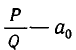
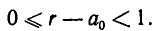
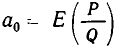
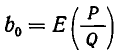
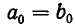
Отсюда следует, что

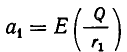
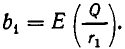
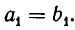
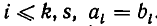
Но точно так же и Отсюда следует Продолжая процесс сравнения соответствующих частных знаменателей, получим для всех Если теперь допустить, например, что k

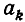
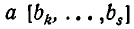
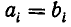
которое невозможно, поскольку — целое число, а — дробное. Точно так же доказывается, что невозможно неравенство k > s. Итак, k = s и для всех i. Однозначность разложе­ния доказана.

Подходящие дроби

Как уже говорилось, цепные дроби служат для получения приближенных значений, имеющих малые знаменатели. Эти приближенные значения получаются так: число разлагают в цепную дробь и обрывают процесс разложения на некотором шагу, заменяя смешанную дробь ее целой частью. Полу­чающиеся таким образом дроби называются подходящими дробями для данной цепной дроби. Иными словами, подходящими дробями для заданной цепной дроби

У цепной дроби с n частными знаменателями имеется ровно n под­ходящих дробей; последняя подходящая дробь равна данной цеп­ной дроби.

Пример:

Вычислим подходящие дроби цепной дроби [1, 2, 3, 4,]:

Чем больше номер подходящей дроби, тем утомительнее ее непосредственное обращение в обыкновенную дробь. При этом все пре­дыдущие вычисления оказываются бесполезными для дальнейшего, все приходится выполнять вновь.

Естественно искать путь вычисления подходящих дробей дан­ной цепной дроби, при котором использовались бы значения предыдущих дробей. Оказывается, для этого можно использовать так называемые рекуррентные соотношения меж­ду тремя последовательными подходящими дробями.

Вернемся к предыдущему примеру. Запишем подходящие дроби следующим образом:

Правило, по которому записаны третья и четвертая подходящие дроби, таково: в числителе записываются два слагаемых — числители двух предыдущих подходящих дробей, а в знаменателе — знаменатели предыдущих подходящих дробей, как показано ниже. И тут и там делается пропуск для множителя:

Оставленное место для множителя заполняется соответствующим частным знаменателем.

Докажем это правило в общем виде. Обозначим числитель и знаменатель i-й подходящей дроби через 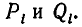В этих обозначениях правило записывается так:

(здесь I = 2, 3, . . . , n).

Доказательство ведется с помощью математической индукции по индексу i.

Проверим сперва правило для i = 2; первые три подходящие дроби имеют вид:

Отсюда следует, что

Таким образом, правило верно при i = 2.

Допустим теперь, что правило верно для i = k — 1, то есть что

Докажем, что это же правило верно и при i=k, а именно, что имеет место равенство:

Чтобы получить k-ю подходящую дробь, надо в (k — 1)-й подходящей дроби (k — 1)-й частный знаменатель заменить на вы­ражение Сделаем эту замену и преобразуем числитель и знаменатель: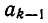

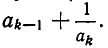
По предположению индукции имеем:

Итак, наша формула верна и при i=k. Значит, она верна при всех Иными словами, мы доказали, что

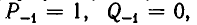
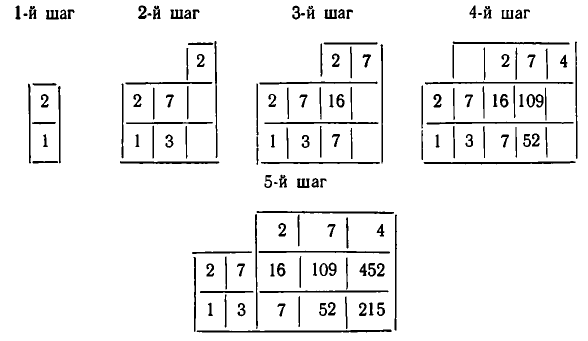
Для того чтобы формулы (3) и (4) не теряли смысла при i = 1, вводят определения которые носят чисто формальный характер, но делают правила (3) —(4) верными и при i = 1.

Покажем, как проводится вычисление, на примере цепной дроби [2, 3, 2, 7, 4]. Вычисление удобно располагать в табличку, которую заполняют последовательно. Первые два столбика заполняют компонентами первых двух подходящих дробей (нулевой и первой под­ходящей дроби), которые вычисляются непосредственно; третий столбик заполняется компонентами второй подходящей дроби, которые находятся по правилу: числитель первой подходящей дро­би умножается на второй частный знаменатель, к полученному про­изведению прибавляется числитель нулевой подходящей дроби: так же находится и знаменатель второй подходящей дроби. Точно так же определяются числители и знаменатели последующих под­ходящих дробей. Вот последовательные шаги заполнения таб­лички:

Значит,

Свойства подходящих дробей

Полученное выше правило вычисления подходящих дробей имеет фундаментальное значение для всей теории цепных дробей. Кроме способа непосредственного вы­числения последовательности подходящих дробей, из него получается ряд важных свойств частных числителей и частных знамена­телей и подходящих дробей цепной дроби.

Рассмотрим некоторые из этих свойств.

1) Докажем, что для i =1, 2, 3, . . . , n имеет место равенство:

Доказательство проведем индукцией по индексу i.

Покажем прежде всего справедливость формулы (1) при i=1. Заметим, что 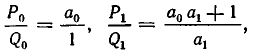откуда

откуда следует, что

то есть формула (1) справедлива при i = 1.

Предположим, что формула (1) справедлива при i = m — 1:

Докажем, что она справедлива и при i = m, то есть что

Для этого выразим 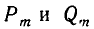по формулам (3) и (4) из п. 5 и сдела­ем соответствующие подстановки:

В силу формулы (1′) получаем:

Итак, из справедливости формулы (1) при i = m — 1 следует ее справедливость при i = m. Значит, она верна при всех значениях i.

2) Докажем, что при i = 1,2,3,… имеет место равенство:

Доказательство:

Преобразуем левую часть равенства (2) и применим свойство (1):

Из последних двух свойств вытекает важное следствие.

3) Пoдходящие дроби цепной дроби несократимы.

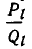
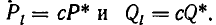
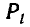
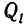
Будем доказывать это утверждение от противного. Предположим, что какая-то дробь сократима. Это значит, что числитель и знаменатель дроби имеют общий множитель. Обозначим его через с; тогда Подставив эти значения и в равенство (1), мы получим:

Но последнее равенство неверно, так как левая часть делится на с, а правая — нет. Следовательно, наше предположение, что частные числитель и знаменатель 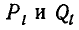имеют общий множитель, не­верно.

Диофантовы уравнения первой степени

Мы знаем, что одно урав­нение с двумя неизвестными, вообще говоря, имеет бесчисленное множество решений. Однако если рассматривать такие уравнения лишь в множестве це­лых чисел, то может оказаться, что уравнение имеет лишь конечное множе­ство решений.

Например, уравнение 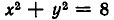имеет бесчисленное множество дей­ствительных решений. Целыми же решениями уравнения являются лишь (2, 2); (— 2, 2); (2, — 2); ( — 2, — 2).

Уравнения, для которых ищутся лишь целые решения, обычно называют диофантовыми.

Вопрос о решении уравнений в целых числах довольно сложен. Мы рас­смотрим сейчас самый простой вид таких уравнений, а именно уравнения вида

где а, b и с — целые числа.

Такие уравнения можно решать с помощью цепных дробей. Для примера рассмотрим

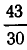
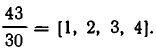
Разложим в цепную дробь: Рассмотрим разность между предпоследней и последней подходящими дробями:

Умножим обе части равенства (2) на 11:

Получилось, что х = 77 и у = — 110 являются решениями заданного урав­нения.

Нетрудно заметить, что решением того же уравнения будет любая пара чисел (х, у), следующим образом выражающихся через целый параметр t:

Этот метод всегда применим, если с делится на наибольший общий дели­тель чисел а и b. В противном случае уравнение не имеет целых решений.

Иногда ставится задача решений диофантовых уравнений в множестве натуральных чисел. Для этого нужно сначала решить его в целых числах, а потом найти значения t, при которых х и у положительны.

В разобранном выше примере для этого нужно решить в целых числах систему неравенств:

Решая ее, находим t = 3, 4, 5, . . .

Подходящие дроби и календарь

Астрономы подсчитали, что время полного оборота Земли вокруг Солнца приближенно равно 365 суткам 5 ча­сам 48 минутам 46 секундам. Если это время выразить в сутках, то получим приближенно 365,2422 суток.

Обратим дробную часть в цепную дробь:

Первые три подходящие дроби:

Первая подходящая дробь 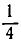показывает, что, считая год равным 365 дням, мы делаем ошибку на четверть суток. За четыре года получается от­ставание на одни сутки. Чтобы устранить это отставание, Юлий Цезарь в 45 году до нашей эры ввел новый («юлианский») календарь, в котором каждый четвертый год считался високосным — в феврале прибавляют один день.

Однако через столетия снова начала накопляться ошибка. Чтобы ее оценить, рассмотрим разность

Таким образом, за каждые 132 года прибавляется лишний день (за 396 лет — 3 лишних дня).

Более точный календарь был введен папой Григорием XXII в 1582 году.

Во-первых, он выкинул в этом году 10 дней (следующий день после чет­верга 4 октября 1582 года именовался пятницей 15 октября), во-вторых, по­становил в каждые четыреста лет три високосных года обращать в простые, а один оставить високосным. При переходе нашей страны на григорианский календарь в 1918 году разница во времени уже возросла до 13 суток, что и составляет разницу между старым и новым стилем.

Приближение цепной дроби подходящими дробями

Выясним теперь характер приближения подходящих дробей к рациональному числу, разложенному в данную цепную дробь. Для этого нам понадобится следующее утверждение.

Теорема:

Пусть дана цепная дробь длины т:

При увеличении последнего знаменателя 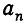дробь увеличивается, если ее длина п четная, и уменьшается, если п нечетно.

Доказательство:

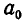
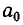
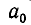
Проведем доказательство с помощью индукции по n. При n = 0 утверждение очевидно. В этом случае «дробь» имеет вид и увеличивается при увеличении (при этом может, увеличиваясь, принимать не только целые, а любые значения).

Пусть теорема уже доказана для дробей длины k. Рассмотрим дробь длины 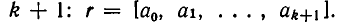Ее можно пред­ставить в виде

— цепная дробь длины k.

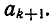
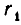
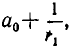
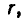
Пусть k + 1 — четное число. Тогда — дробь нечетной дли­ны k. Поэтому по предположению индукции она уменьшается при увеличении Но при уменьшении выражение то есть увеличивается.

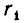
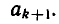
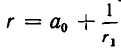
Если же k + 1 — нечетное число, то — дробь четной длины k и по предположению индукции увеличивается при увеличении Но тогда уменьшается при увеличении

Итак, предположив, что теорема верна для n = k мы доказали ее справедливость при n = k + 1. Так как при n = 0 она верна, то она справедлива для всех значений n.

Из теоремы 2 вытекает важное

Следствие:

Всякая четная подходящая дробь не больше значения цепной дроби у а всякая нечетная подходящая дробь не меньше этого значения.

Доказательство:

Пусть дана дробь

— ее k-я подходящая дробь. Дробь r можно записать в виде

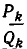
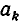
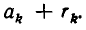
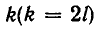
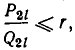
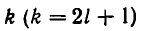
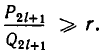
Таким образом, цепная дробь r получается из подходящей дроби увеличением последнего знаменателя до значения Из теоремы 2 следует, что если k— четное число, то дробь при этом увеличивается, а если k — нечетно, то она уменьшается. Значит, при четном имеем: а при нечетном имеет место Следствие доказано.

Из этого следствия вытекает, что если 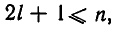то справедливо неравенство

Более точную информацию о характере приближения подходящих дробей 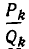к числу r дает следующая

Теорема:

Имеют место неравенства

Доказательство:

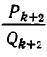
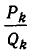
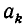
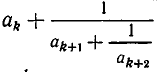
Подходящая дробь получается из подходящей дроби заменой частного знаменателя выраже­нием . Так как это выражение больше то при четном k подходящая дробь увеличивается, а при нечетном умень­шается. Отсюда и вытекает теорема 3.

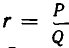
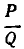
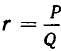
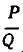
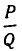
Из теоремы 3 и следствия из теоремы 2 вытекает, что четные подходящие дроби приближаются к числу , монотонно возрастая и оставаясь все время не больше, чем . Нечетные подходя­щие дроби приближаются к , монотонно убывая и оставаясь все время не меньше, чем . При этом равняться — может лишь последняя подходящая дробь. Итак, мы имеем:

Знак равенства имеет место слева, если n = 2l, и справа, если n = 2l + 1.

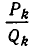
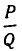
Оценим теперь отклонение подходящей дроби от числа .

По формуле (1) из п. 6 имеем:

Из формул (1) и (2) следует, что

Так как

Бесконечные цепные дроби

Разложение иррациональных чисел в цепные дроби: До сих пор мы разлагали в цепные дроби рациональные числа. При этом процесс нахождения частных знаменателей сводился на каждом шагу к выделению целой части неправильной обыкновенной дроби.

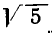
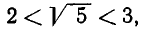
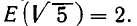
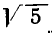
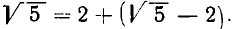
Возьмем теперь какое-нибудь иррациональное число, например Алгоритм Евклида здесь неприменим. Однако выделение целой части этого числа — вполне реальная задача. В самом деле, ясно, что так что Значит, число представимо в виде Во втором слагаемом уничтожим иррациональность в числителе:

Таким образом,

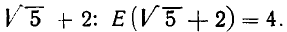
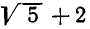
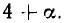
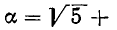
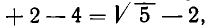
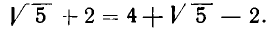
Выделим целую часть числа Значит можно представить в виде Ясно, что поэтому Снова уничтожим иррациональность в числителе второго слагаемого:

В итоге получилось:

Проделаем еще один аналогичный шаг:

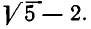
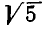
Нетрудно заметить, что процесс выделения целой части и образования цепной дроби в данном примере не имеет конца. В каждом новом знаменателе будет появляться 4 и слагаемое По­этому ясно, что представляется в виде бесконечной цепной дроби:

Мы видим, что цепные дроби являются хорошим аппаратом для вычисления квадратных корней.

Проверим, насколько полезен этот способ — как точно находится зна­чение 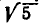с помощью цепных дробей.

Для сравнения будем брать подходящие дроби и обращать их в обыкно­венные, а затем полученные обыкновенные — в десятичные. Десятичные приб­лижения, получаемые из подходящих дробей, будем сравнивать со значени­ем 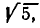взятым из таблиц Брадиса

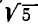
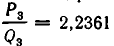
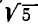
Получилось, что уже для четвертой подходящей дроби результат приближе­ния по точности не уступает значению, указанному в четырехзначной таблице значений квадратных корней. Больше того, значение той же подходящей дроби равно значению , указанному в пятизначной таблице. Вообще, нахождение приближений с помощью цепных дробей — мощный вычислительный аппарат.

Возьмем произвольное иррациональное число а. Выделим его целую часть и обозначим ее через

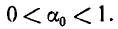
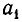
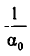
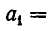
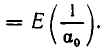
где Далее, пусть — целая часть , то есть Тогда

гдe

Пусть 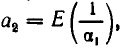тогда

Через n шагов получим:

где 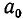— целое число, — натуральные числа и 0

для которой — натуральные числа ( может быть целым числом любого знака).

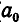
Построим для полученной дроби последовательность ее подходящих дробей (в отличие от случая разложения рациональных чи­сел эта последовательность бесконечна). Можно доказать, что последовательность

подходящих дробей сходится к разлагаемому числу а. Мы опускаем здесь это доказательство.

Подходящие дроби и наилучшие приближения иррациональных чи­сел рациональными

Мы научились изображать любые числа, как рацио­нальные, так и иррациональные, в виде цепных дробей. Выясним теперь, в чем заключаются преимущества и недостатки такого изображения.

Основное преимущество записи чисел в виде цепных дробей по сравне­нию с их записью в виде систематических (например, десятичных) дробей состоит в том, что эта запись не зависит от выбора системы счисления. Ведь неполные знаменатели получались путем выделения целой части из неправиль­ных дробей, а эта операция при любой системе счисления приводит к одному и тому же результату (конечно, с точностью до записи в разных системах счисления самих неполных знаменателей). Поэтому запись числа в виде цеп­ной дроби отражает его «существенные» арифметические свойства, а не свой­ства, связанные с выбором той или иной системы счисления.

Например, при записи рационального числа в виде систематической дроби может получиться либо конечная дробь, либо бесконечная периоди­ческая или смешанная) дробь. При записи же рационального числа в виде цепной дроби всегда получается конечная дробь, причем это характерно только для рациональных чисел. Можно доказать, что квадратичные иррациональности, и. только они, представляются в виде периодических цепных дробей. Выразить же условие того, что данное число является квадратичной ир­рациональностью, в терминах систематических дробей невозможно.

Но самое важное преимущество цепных дробей по сравнению с система­тическими заключается в том, что они дают наилучшие приближе­ния данного числа с помощью дробей, имеющих не слишком большие зна­менатели. Уточним это утверждение.

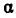
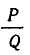
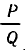
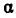
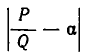
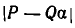
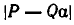
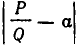
Пусть даны число и несократимая дробь . Естественной мерой откло­нения от является . Однако в теоретических вопросах оказа­лось удобнее рассматривать в качестве меры отклонения число . Ясно, что если мало, то тем более мало число . Обратное верно не всегда, так как знаменатель Q может оказаться большим числом.

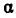
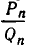
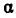
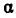
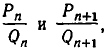
Пусть число разложено в цепную дробь. Легко оценить отклонение подходящей дроби от . Так как лежит между то имеем:

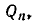
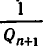
Оказывается, для любой дроби, знаменатель которой не превосходит отклонение больше, чем . Иными словами, справедлива следующая

Теорема:

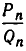
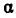
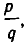
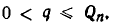
Если — подходящая дробь для разложения числа в цепную дробь, то для любой дроби такой, что выполняется неравенство

Единственным исключением является подходящая дробь 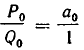для числа вида

Доказательство этой теоремы мы опускаем.

Теорема 4 показывает, что подходящие дроби являются наилучшими приближениями для числа 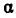по сравнению со всеми дробями, знаменатель которых не превосходит знаменателя подходящей дроби. Именно это свой­ство послужило причиной введения цепных дробей в математику и деталь­ного изучения их теории. В конце XVII века голландский математик и фи­зик Гюйгенс хотел построить модель Солнечной системы с помощью зубчатых колес. При этом возникла задача определить число зубцов так, чтобы отно­шение этих чисел для двух связанных между собой колес было по возможнос­ти близко к отношению времен обращения соответствующих планет, при­чем число зубцов не должно быть слишком большим. Таким образом, встал вопрос об отыскании рациональной дроби, числитель и знаменатель которой были бы не слишком большими числами и которая наилучшим образом приближала число . С помощью теории цепных дробей задача была решена.

Отметим, что цепные дроби как аппарат для изображения действитель­ных чисел имеют и недостатки: дело в том, что над действительными числа­ ми, изображенными в виде цепных дробей, практически трудно выполнять арифметические операции — сложение, вычитание, умножение и деление. (Попробуйте, например, сложить или перемножить дроби

[2, 1, 3, 1, 4] и [3, 2, 4, 6, 8 ],

не переводя их в обыкновенные.)

Цепные дроби как вычислительный инструмент

Рассмотрим некоторые примеры приближения иррациональных чисел подходя­щими дробями.

Начнем с числа Разлагая число в цепную дробь, получаем: Найдем подходя­щие дроби для этой цепной дроби:

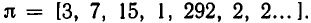
а затем составим таблицу для вычисления последующих дробей с помощью рекуррентного правила:

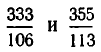
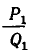
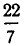
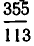
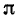
Получаем подходящие дроби . Приближение , равное , было известно еще Архимеду, а приближением пользовался Андриан Меций еще в конце XVI столетия. Первое приближение очень удобно тем, что знаменатель 7 очень невелик. Во второй дроби при сравнительно небольшом знаменателе 113 получается приближенное значение с высокой точностью.

Чтобы оценить эту точность, используем формулу

В нашем случае

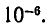
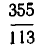
то есть точность полученного ответа превышает Обращая дробь в десятичную, получаем:

С помощью цепных дробей можно выполнять вычисление логарифмов при любом основании. Вычислим, например, 1g 20. Полученный результат будем сравнивать со значением 1g 20, взятым из таблицы Брадиса:

Обозначим искомое число через х; 1g 20 = х. Значит,

Ясно, что 1

Последнее равенство возведем в степень

Подставим значение 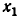в равенство (2):

Отсюда 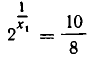и потому . Но тогда

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Решение диофантовых уравнений с помощью цепных дробей. Диофантово уравнение: методы решения с примерами. А ведь вы знаете кое-что о диофантовых уравнениях…

Министерство образования и науки Республики Казахстан

Направление: математическое моделирование экономических и социальных процессов.

Тема: Решение диофантовых уравнений первой и второй степени

ГУ «Экономический лицей»

Дранная Наталия Александровна

ГУ «Экономический лицей»

Заведующий кафедрой математики и методики преподавания математики Семипалатинского государственного педагогического института, кандидат физико- математических наук, доцент

Жолымбаев Оралтай Муратханович

Глава 1.О диофантовых уравнениях. 4

Глава 2.Методы решения. 6

2.1.Алгоритм Евклида. 6

2.2.Цепная дробь. 8

2.3.Метод разложения на множители. 9

2.4.ИСпользование четности. 10

2.5.Другие методы решения диофантовых уравнений. 10

Список литературы. 13

«Достопочтеннейший Дионисий, зная, что ты ревностно хочешь научиться решению задач, касающихся чисел, я попытался изложить природу их и могуще­ство, начиная с тех оснований, на которых покоится эта наука.

Может быть, этот предмет покажется тебе затруднительным, поскольку ты еще с ним незнаком, а начинающие не склонны надеяться на успех. Но он станет тебе удобопонятным благодаря твоему усердию и моим пояснениям, ибо страстная любовь к науке помогает быстро воспринять учение»

Таким посвящением открывается «Арифметика» Диофанта Александрий­ского.

Диофант представляет одну из занимательных загадок в истории математики. Мы не знаем, кем был Диофант, точные года его жизни, нам не известны его предшественники, которые работали бы в той же области, что и он.

На могиле Диофанта есть стихотворение-загадка, решая которую нетрудно подсчитать, что Диофант прожил 84 года. О времени жизни Диофанта мы можем судить по работам французского исследователя науки, Поля Таннри, и это, веро­ятно, середина 3 в.н.э.

Наиболее интересным представляется творчество Диофанта. До нас дошло 7 книг из 13, которые были объединены в “Арифметику”.

В этой книге Диофант (3 век) суммировал и расширил накопленный до него опыт решения неопределенных алгебраических уравнений в целых или рацио­нальных числах. С тех пор эти уравнения стали называться диофантовыми.

Вот примеры таких уравнений: х 2 +у 2 =z 2 , х 2 = у 3 +5у + 7.

Интерес к диофантовым уравнениям связан, видимо, с самой природой чело­века – сохранившиеся документы обнаруживают его следы в глубине тысячеле­тий. Еще в Древнем Вавилоне занимались поисками пифагоровых троек – цело­численных решений уравнения

Диофантовы уравнения позволяют решать алгебраические задачи в целых числах. «Арифметика» Диофанта легла в основу теории чисел нового времени.

Цель данного исследования: найти различные методы решения неопределенных уравнений.

Задачи исследования: научиться решать неопределенные уравнения первой и второй степени с помощью алгоритма Евклида, с помощью цепных дробей или разложением уравнения на множители

Глава 1. О диофантовых уравнениях.

Диофантовыми уравнениями называют алгебраические уравнения или системы алгебраических уравнений с целыми коэффициентами, для которых надо найти целые или рациональные решения. При этом число неиз­вестных в уравнениях должно быть не менее двух (если не ограничиваться только целыми числами). Диофантовы уравнения имеют, как правило, много решений, поэтому их называют неопределенными уравнениями.

К диофантовым уравнениям приводят задачи, по смыслу которых неизвест­ные значения величин могут быть только целыми числами.

Рассмотрим одну задачу: За покупку нужно уплатить 1700 р. У покупателя имеются купюры только по 200 и 500 р. Какими способами он может распла­титься? Для ответа на этот вопрос достаточно решить уравнение 2х +5у = 17 с двумя неизвестными х и у. Такие уравнения имеют бесконечное множество реше­ний. В частности, полученному уравнению отвечает любая пара чисел вида
. Для нашей практической задачи годятся только целые неотрицатель­ные значения х и у (рвать купюры на части не стоит). Поэтому приходим к поста­новке задачи: найти все целые неотрицательные решения уравнения 2х +5у = 17. Ответ содержит уже не бесконечно много, а всего лишь две пары чисел (1;3) и (6; 1).

Таким образом, особенности диофантовых задач заключаются в том, что: 1) они сводятся к уравнениям или систе­мам уравнений с целыми коэффициентами; 2) решения требуется найти только целые, часто натуральные.

Перед тем как рассмотреть методы решения неопределенных уравнений представим некоторые определения и утверждения, необходимые для дальнейшего изложения.

Определение Пусть a,b  Z , b ≠ 0. Числа q  Z и r  <0,1. |b|-1>называются соответственно неполным частным и остатком от деления a на b, если выполнено равенство

При этом, если r = 0, то говорят, что a делится на b, или что b является делите­лем a (обозначение a b или b| a).

Диофантовы уравнения можно записать в виде

P(x 1 , x 2 , . x n) = 0,

где P(x 1 , . x n) — многочлен с целыми коэффициентами.

При исследовании диофантовых уравнений обычно ставятся следующие во­просы:

имеет ли уравнение целочисленные решения;

конечно или бесконечно множество его целочисленных решений;

решить уравнение на множестве целых чисел, т. е. найти все его целочислен­ные решения;

решить уравнение на множестве целых положительных чисел;

решить уравнение на множестве рациональных чисел.

Отметим, что проблема решения уравнений в целых числах решена до конца только для уравнений с одним неизвестным, для уравнений первой степени и для уравнений второй степени с двумя неизвестными. Для уравнений выше второй степени с двумя или более неизвестными достаточно трудной является даже за­дача существования целочисленных решений. Например, не известно, имеет ли уравнение

x 3 + y 3 + z 3 = 30

хотя бы одно целочисленное решение. Более того, доказано, что в принципе не существует единого алгоритма, позволяющего за конечное число шагов решать в целых числах произвольные диофантовы уравнения.

Глава 2. Методы решения.

2.1 Алгоритм Евклида.

Можно найти наибольший общий делитель натуральных чисел а и b, не раскладывая эти числа на простые множители, а применяя процесс деления с ос­татком. Для этого надо разделить большее из этих чисел на меньшее, потом меньшее из чисел на остаток при первом делении, затем остаток при первом деле­нии на остаток при втором делении и вести этот процесс до тех пор, пока не произойдет деление без остатка (т.к. остатки убывают, то это на каком-то шаге случится). Последний отличный от нуля остаток и есть искомый НОД (а, b).

Чтобы доказать это утверждение, представим описанный процесс в виде следующей цепочки равенств: если а>b, то

Здесь r 1 , …, r n – положительные остатки, убывающие с возрастанием но­мера. Из первого равенства следует, что общий делитель чисел а и b делит r 1 и общий делитель b и r 1 делит а, поэтому НОД (а, b) = НОД (b, r 1). Переходя к сле­дующим равенствам системы, получаем:

НОД(а, b) = НОД (b, r 1) = НОД (r 1, r 2) = …

…= НОД (r n -1 , r n) = НОД (r n , 0) = r n .

Таким образом, решая диофантовы уравнения первой степени ax + by = с, можно применять следующие теоремы:

Теорема1.. Если НОД (a, b) = 1, то уравнение ax + by = 1 имеет, по меньшей мере, одну пару (x, y) целого решения.

Теорема 2. Если НОД (a, b) = d > 1, и число с не делится на d, то уравнение ах + by = с не имеет целого решения.

Доказательство. Предположим, что уравнение ах + by = с имеет целое реше­ние (х 0 , y 0). Так как, аd, bd, то получим, что с = (ах + by)d. Это противоречит условиям теоремы и тем самым теорема доказана.

Теорема 3. Если НОД (a, b) = 1,то все целые решения уравнения ах + by = с опре­деляются формулой:

Здесь (х 0 , y 0) – целое решение уравнения ах + by = 1, а t – произвольное целое число.

Пример 1. Решить в целых числах уравнение 54х + 37у = 1.

По алгоритму Евклида а = 54, b = 37. Подставляем данные под алгоритм и получаем:

54=371+17, остаток от деления 17 = 54-371

37 = 172+3 , 3 = 37-172

17 = 35+2 , 2 = 17- 35

3 = 21+1 , 1 = 3 — 21

После нахождения единицы выражаем через неё значения а и b:

1 = 17 — (37- 172) 4;

1 = (54- 371) 9 — 374;

1 = 549 — 379 — 374;

Следовательно, х 0 = 9, у 0 = -13. Значит, данное уравнение имеет следующее решение
.

Пример 2. Требуется найти целое решение уравнения 15x + 37y = 1.

1-й метод. Воспользуемся разложением единицы:

1 = 15*5 + 37*(-2).Ответ: x = 5, y = -2.

2-й метод. Применяя алгоритм Евклида, имеем: 37 = 15*2 + 7, 15 = 2*7 + 1. Отсюда 1 = 15 – 2*7 = 15 – 2(37 – 15*2) = 15*5 + (-2)*37. Тогда x о = 5, y о = — 2. Общее решение уравнения есть система .

Пример 3 . В уравнении 16x + 34y = 7, НОД (16, 34) = 2 и 7 не делится на 2,то нет целых решений.

2.2 Цепная дробь

Одним из применений алгоритма Евклида является представление дроби в виде

Где q 1 – целое число, а q 2 , … ,q n – натуральные числа. Такое выражение на­зывается цепной (конечной непрерывной) дробью.

с взаимно простыми коэффициентами a и b имеет решение

,
,

где
— предпоследняя подходящая дробь к цепной дроби, в которую раскладывается дробь .

Если для заданной цепной дроби с последовательными частными q 1 , q 2 ,…,q n несократимые дроби

, , …,

являются результатами свертывания подходящих дробей
,
, и т.д. , порядка 1, 2, …, n соответственно,то

,
, …, n.

,

Где — последняя подходящая дробь к цепной дроби, в которую раскладывается дробь . Так как дроби и несократимы, то , и

.

Умножая обе части последнего равенства на (-1) n , имеем

То есть пара чисел , , где n-порядок цепной дроби, является решением уравнения .

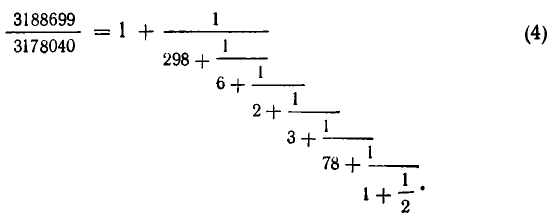
Пример. Для перевозки большого количества контейнеров по 170 кг и по 190 кг выделены трехтонные машины. Можно ли ими загружать машины полно­стью?

Пусть х и у количество контейнеров по 170 и 190 кг соответственно, тогда имеем уравнение

После сокращения на 10 уравнение выглядит так,

Для нахождения частного решения воспользуемся разложением дроби в цепную дробь

Свернув предпоследнюю подходящую к ней дробь в обыкновенную

Частное решение данного уравнения имеет вид

х 0 = (-1) 4 300*9=2700, у 0 =(-1) 5 300*8=-2400,

а общее задается формулой

х=2700-19k, y= -2400+17k.

откуда получаем условие на параметр k

2.3 Метод разложения на множители

Данный метод и все последующие применяются к решению диофантовых уравнений второй степени.

Решение. Запишем уравнение в виде

Произведение двух целых чисел может равняться 1 только в том случае, когда оба они равны 1. Т. е. исходное уравнение равносильно совокупности

с решениями (0,0) и (2,2).

2.4 Использование четности

Задача 2. Решить в простых числах уравнение

Решение. Рассмотрим два случая в зависимости от четности переменной x.

a) Пусть x — нечетное число. Подстановка x = 2t + 1 приводит исходное уравне­ние к виду

(2t + 1) 2 — 2y 2 = 1,

Следовательно, 2 | y 2 . Так как y — простое число, то y = 2. Отсюда

b) Пусть x — четное число. Так как x — простое число, то x = 2. Следовательно, т. е. уравнение неразрешимо в простых числах.

Следовательно, уравнение имеет в классе простых чисел единственное реше­ние (3;2).

2.5 Другие методы решения диофантовых уравнений

Задача 3. Доказать, что уравнение

имеет бесконечно много решений в натуральных числах.

Решение. Нетрудно заметить, что (3,2) — одно из решений исходного уравне­ния. С другой стороны из тождества

(x 2 + 2y 2) 2 — 2(2xy) 2 = (x 2 — 2y 2) 2

следует, что если (x, y) — решение данного уравнения, то пара (x 2 + 2y 2 , 2xy) также явля­ется его решением. Используя этот факт, рекуррентно определим бесконеч­ную последовательность (x n , y n) различных решений исходного уравнения:

(x 1 , y 1) = (3,2) и x n +1 = x n 2 + 2y n 2 , y n +1 = 2x n y n , n  N * .

Задача 4. Доказать, что уравнение

неразрешимо в целых положительных числах.

Решение. Нетрудно заметить, что исходное уравнение равносильно уравнению

x 2 + x + 1 = (2y + 1) 2 .

Следовательно, x 2

Задача 5. Решить в целых числах уравнение

x + y = x 2 — xy + y 2 .

Решение. Положим t = x + y. Так как

то должно выполняться неравенство откуда t  .

Современное обозначение непрерывных дробей предложил выдающийся учёный Христиан Гюйгенс (1629-1695).

К цепным дробям Гюйгенс обратился при построении планетария в Париже. Он хотел получить наилучшее приближение для отношения периодов обращения планет. Эти отношения и отношения чисел зубцов соответствующих связанных между собой шестерён планетария должны были совпадать. Но числа зубцов шестерен по техническим причинам не могут быть очень большими. Необходимо было так их подобрать, чтобы полученные отношения как можно меньше отличались от истинных. Гюйгенс обратился к цепным дробям и с их помощью нашел решение стоящей перед ним задачи.

В заключении отметим преимущества и недостатки цепных дробей по сравнению, например, с десятичными. Удобство заключается в том, что их свойства не связаны ни с какой системой счисления. По этой причине цепные дроби эффективно используются в теоретических исследованиях. Но широкого практического применения они не получили, так как для них нет удобных правил выполнения арифметических действий, которые имеются для десятичных дробей.

Данная тема актуальна тем, что диофантовы уравнения используются так же в инженерии, биологии и т.д. Например, при подсчете хромосом первого поколе­ния.

Для начала выберем пять случайных решений: 1=

1-е поколение хромосом и их содержимое.

Главное свойство диофантовых уравнений в том, что мы не перебираем все варианты решений подряд, а приближаемся от случайно выбранных решений к лучшим.

Журнал «Квант» 1970г. №7

«Энциклопедия юного математика» 520 с.

Виленкин Н.Я. «За страницами учебника математики» (10-11 класс).- Москва: «Просвещение» 1996-320 с.

Шыныбеков Н.А. «Алгебра 8» Алматы «Атамұра» 2004-272 с.

И.Н.Сергеев «Примени математику» 1989г.- 240 с.

Кожегельдинов С.Ш. «Некоторые элементы теории диофантовых уравнений в упражнениях и задачах»

Пичугин Л.Ф. «За страницами учебника алгебры», М., 1990г., 224с.

Глейзер Г.И. «История математики в школе 10-11», 351с

Гусев В.А., Орлов А.И. и др. «Внеклассная работа по математике в 6-8 классах», М., 1984г., 286 с.

Петраков И.А. «Математика для любознательных», М., 2000г. 256с.

Решить в целых числах уравнение 127x — 52y + 1 = 0. Ответ: x = 9 + 52t, y = 22 + 127t, t  Z .

Решить в целых числах уравнение 107х + 84у = 1.

Решить в целых числах уравнение 3x 2 + 4xy — 7y 2 = 13. Указание. Применить разложение на множители.
Ответ: (2,1), (-2,-1).

Доказать, что уравнение y 2 = 5x 2 + 6 не имеет целочисленных решений.
Указание. Рассмотреть уравнение по модулю 4.

Доказать, что уравнение x 2 — 3y 2 = 1 имеет бесконечно много решений в целых числах.
Указание. Использовать реккурентное соотношение между решениями.

Решить уравнение: 17х +13у=5.

Докажите, что любую денежную сумму, выраженную целым числом рублей, большим 7, можно уплатить без сдачи, имея лишь трёхрублёвые и пятирублёвые купюры в достаточном количестве.

Требуется разлить 20,5 литра сока в банки по 0,7 литра и 0,9 литра так, чтобы все банки оказались полными. Сколько каких банок надо заготовить? Какое наименьшее количество банок при этом может понадобиться?

Причем, с тремя неизвестными, а также решают.

Генетические алгоритмы и их практическое применение

Strategies). Ближе ко второму полюсу — системы, которые. идеях адаптации и эволюции. Степень мутации в данном случае. математика Диофанта.26 Рассмотрим диофантово уравнение : a+2b+3c+4d . Коэффициенты выживаемости первого поколения хромосом (набора решений ) Так.

Выдающаяся роль Леонарда Эйлера в развитии алгебры геометрии и теории чисел

. решении уравнений . Он указывал, что решение уравнений второй , третьей и четвертой степеней приводится к уравнениям соответственно первой , второй и третьей степени ; эти последние уравнения . целочисленном решении систем диофантовых уравнений высших степеней и.

Моделирование парожидкостного равновесия в четырехкомпонентной смеси ацетонтолуолн-бутанолдиметилформамид

Являются составляющими единой системы диофантовых уравнений и взаимно дополняют. Эффективность принимаемых решений в значительной степени определяется особенностями. молекулу первого компонента, другой – молекулу второго компонента. Согласно уравнению .

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 28 города СМОЛЕНСКА

СМОЛЕНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Выполнил работу: Гончаров Евгений Игоревич,

учащийся 11 класса

Руководитель: Солдатенкова Зоя Александровна,

Почему меня заинтересовала данная тема?

Как-то раз, листая учебник, я наткнулся на небольшую врезку о диофантовых уравнениях. Я сразу же заметил, что текстовые задачи в рамках этой темы имеют интригующее, порой комичное, условие, а в силу большого количества различных методов их решения, они вовсе не кажутся типовыми. Кроме того, некоторые вызвали у меня затруднение.

Находя пути их рационального решения, я стал плотнее знакомиться с данной темой. Чем глубже я погружался — тем больше сложных и интересных задач встречал, тем больше возникало вопросов. Вскоре я осознал, что большая часть этой темы лежит за рамками школьной программы.

Поэтому я не стал опережать события и углубляться в теорию (КТО, 10 проблема Гильберта, Великая теорема Ферма и прочее). А начал осваивать исключительно алгоритмы решения диофантовых уравнений и систем уравнений, параллельно знакомясь с историей их открытия.

Диофант Александрийский — древнегреческий математик. Летописи не сохранили практическиникаких сведений об этом ученом. Диофант представляет одну занимательных загадок в истории математики. из Мы не знаем, кем он был, точные года его жизни, нам не известны его предшественники, которые работали бы в той же области, что и сам Диофант:

Диофант цитирует Гипсикла Александрийского (древнегреческого математика и астронома, жившего во II веке до н. э.);

О Диофанте пишет Теон Александрийский (греческий математик эпохи позднего эллинизма, философ и астроном, живший в III веке н.э.);

Свои работы Диофант посвящаетДионисию Александрийскому (епископу,жившему в середине III в. н. э.). Таким образом, ученые предполагают, что этот математик жил в IIIв.н.э.

В антологии МаксуимаПлануда (греческого монаха XIV в. н.э.) содержится эпиграмма-задача „Эпитафия Диофанта»:

Прах Диофанта гробница покоит; дивись ей — и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругой он обручился.

С нею, пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

(Пер. С. Н. Боброва).

Эта задача сводится к составлению и решению простейшего линейногоуравнения:

где х -количество лет, прожитых Диофантом.

х=84 — вот сколько лет прожил Диофант.

И за эти годы Диофант написал сочинения Об измерении поверхностей и Об умножении , трактат О многоугольных числах . Основнымже произведением Диофанта является Арифметика в 13 книгах.

К сожалению, далеко не все его работы сохранились. В тех, что дошли до нас, содержится 189 задач с решениями, сводящимися к определенным уравнениям первой и второй степеней и неопределенным. Вклад этого ученого в развитие математики огромен.

Диофант вводит специальные символы для вычитания, сокращенные слова для отдельных определений и действий. То есть именно он был автором первого алгебраического языка.

В честь Диофанта назван кратер на Луне.

Однако Диофант не искал общих решений, а довольствовался каким-нибудь одним, как правило, положительным решением неопределенного уравнения.

Диофантовы уравнения как математическая модель жизненных ситуаций

Каждый человек, даже бесконечно далекий от математики, встречался и, более того, — решал простейшие диофантовы уравнения, сам того не зная. Действительно, они служат математической моделью ко многим задачам, возникающим на бытовом уровне.

На складе есть ящики с гвоздями, массой по 16, 17 и 40 кг. Сможет ли кладовщик выдать 100 кг гвоздей, не раскрывая ящиков?

Легко заметить, что 17 кг +17кг +16 кг=50 кг. Тогда, что бы выдать 100 кг (в 2 раза больше) необходимо взять 4 ящика по 17 кг и 2 ящика по 16 кг.

Ответ: Да, сможет.

Здесь нам повезло: решение свелось к простейшему перебору, а ответ оказался очевидным. Рассмотрим еще одну задачу:

В загоне находятся одноглавые сороконожки и трехглавые змеи. Всего у них 298 ног и 26 голов. Сколько ног у трехглавых змей?

Пусть в загоне было х сороконожек, и y Горынычей, причем у каждого змея по p ног. Сразу же оговорим, что каждая из этих переменных должна быть целой и положительной. Тогда:

y>0 p>0p>0 120-742/y>0>0y>0y>0y>0

Так как p целое, то p=27,25 нам не подходит.

Эта задача была несколько сложнее первой, но путем введения ограничений на переменные мы смогли сузить перебор всего до двух случаев. Идем дальше:

Требуется разлить 20,5 литра сока в банки по 0,7 литра и 0,9 литра так, чтобы все банки оказались полными. Сколько каких банок надо заготовить? Какое наименьшее количество банок при этом может понадобиться?

Пусть xколичество банок по 0,7 литра, а у — 0,9 литра. Тогда составим уравнение:

Очевидно, что прямой перебор чисел в лоб займет уйму времени. А в мире нет места для некрасивой математики ©Г. Харди.

Рассмотрим метод решения подобных уравнений, а потом вернемся непосредственно к нашей задачи и доделаем ее.

Диофантово уравнение имеет вид:(x1,x2…xn)=0, где P — целочисленная функция, а переменные xi принимают целые значения. Решая задачу № 2, мы столкнулись с уравнением вида ax+by=c, где a,b и с целочисленные коэффициенты, а x и у — переменные, принимающие только целые значения. Это — линейное диофантово уравнение с двумя неизвестными.

Общий метод для решения таких уравнений возник в Индии в XII веке. Его появление было вызвано астрономическими запросами и календарными

расчетами. Первые намеки на общее решение диофантовых уравнений сделал Ариабхатт. Сам же метод был создан Бхаскарой и Брахмагуптой. Сейчас он известен как метод рассеивания. Разберем его на примере:

Пример № 1: Найти все целые решения уравнения 19х-8у=13.

Выразим у через х (так как коэффициент при у наименьший) и выделим целую часть:

у= (19x-13)/8 = (3х-13)/8 +2х

Выражение (3х-13)/8 должно быть целым. Обозначим его k.

Тогда 8k=3x-13. Повторим проделанную выше операцию:

x=(8k+13)/3=2k+(2k+13)/3= (2k+13)/3. Тогда 3h=2k+13,=(3h-13)/2=(h-13)/2+h= (h-13)/2. Тогда 2p= h-13. h=13+2p

Из равенства (4) очевидно, что h принимает целые значения при любых целых значениях p.

Путем последовательных подстановок (4) находим выражения для неизвестных: k=13+3p, x= 39+8p и, наконец, у=91+18p.

Теперь, обладая достаточным запасом знаний, вернемся к задачи № 3.

х=29+(2-9у)/7; пусть t=(2-9у)/7, где t — целое число;

t=2-9y; t=(2-2y)/7-y; пусть (2-2y)/7=p, где p — целое число;

Y=7k, где kцелое;y=1-7k, где k — целое число. Тогда x=28+9k.

То есть kможет принимать значения: -3,-2,-1,0.

То есть наименьшему количеству банок соответствует наименьшее k.

Ответ: (28+9k;1-7k), где kпринимает значения -3,-2,-1,0. Наименьшее количество банок 23.

Задачи на разложение числа

Стоит заметить, что текстовые задачи, сводящиеся к нахождению числа, знаю его делители и остатки, занимают особое, почетное место, среди текстовых задач по данной теме. Они же и наиболее сложные, а значит интересные. Рассмотрим некоторые из них.

Крестьянка несла на базар корзину яиц. Неосторожный всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая возместить ущерб, он спросил у крестьянки, сколько яиц было в корзине. Она ответила, что число яиц не знает, но когда она раскладывала их по 2, по 3, по 4, по 5 и по 6, то каждый раз одно яйцо оставалось лишним, а когда она разложила по 7, лишних яиц не осталось. Какое наименьшее количество яиц могла нести крестьянка на базар?

Решение: Обозначим за n искомое количество яиц, тогда составим систему уравнений:

2a+1 n-1=2a (1)=3b+1 n-1=3b (2)=4c+1 n-1=2*2c (3)=5d+1 n-1=5d (4)=6e+1 n-1=2*3e (5)=7fn=7f

Из уравнений (1), (2),(3),(4),(5) следует, что число n-1=2*3*2*5k, где kцелое;

При подстановке полученного n в (7) уравнение получаем: 60k+1=7f.

f= (60k+1)/7 = (4k+1)/7 + 8k;=(4k+1)/7,где rцелое, (1)

7r=4k+1; 4k=7r-1; k=(3r-1)/4+r;=(3r-1)/4,где sцелое

3r-1=4s; 3r=4s+1;r= (s+1)/3+r;= (s+1)/3,где u целое,тогда

то есть s всегда принимает целые значения при любом целочисленном u. Путем последовательных подстановок получаем:

r=4u-1; k=7u-2; f=420u -119.

Очевидно, что при u=1, f принимает наименьшее положительное значение, а именно 301.

* Следует заметить, что не обязательно слепо следовать этому алгоритму до самого победного конца. Фактически, в рамках условия задачи, нам не обязательно отыскивать все возможные целые значения k: достаточно лишь одного, наименьшего. И уже после (1) преобразования очевидно, что искомое нами k равно 5, а значит f=60*5+1=301.

Предположим, что имеется некоторое количество туристов. Разбив их на тройки, получаем в остатке 2, разбив на пятерки — 3, разбив на семерки — 2. Сколько туристов в группе, если всего их число не превосходит 100 человек.

Пусть всего было k туристов. Тогда:

3a+2 k=3a+2=5b+3 5b+3=3a+2=7c+2 7c+2=3a+2

И тут очевидная часть нашего решения заходит в тупик. Что бы из него выйти необходимо вспомнить, что:

1) a*b+c?c (moda) ? c (modb). Например, 15 ? 1 (mod 7), то есть число 15 дает в остатке 1 при делении 7.

2) a*b+d ? c (modr) ó a*b ? c-d (modr) ó b ? a(c-d) (modr) óa? b(c-d) (modr). Тогда:

a+2 ? 3 (mod 5) 3a= 1 (mod 5) a ? 3 (mod 5)

a+2 ? 2 (mod 7) 3a= 0 (mod 7) 3a ? 0 (mod7)

3a+2 k=3a+2= 3 +5p, гдеpцелоеa=3 + 5p

15p ? 0 (mod 7) p= -135 (mod 7)

3a+2 k=3a+2k=105d-2014=3 + 5pa=35d-672 a=35d-672=-135 + 7d, гдеdцелоеp=-135 + 7dp= -135 + 7d

Итак, k=105d-2014. Если d=20, то k = 86, если d 20, то k>100. Ответ: 86.

Давайте попробуем придать ей практическую полезность, например, выведем общую формулы для экскурсовода для подсчета туристов. Пусть r1, r2, r3 остатки при делении общего числа туристов на группы по 3, 5,7 соответственно, а общее количество туристов по-прежнему не будет превышать 100 человек. Аналогичнорассуждая, получаем:

3a+r1 3a? (r2-r1) (mod 5)a=3(r2-r1) + 5d, гдеdцелое=5b+r2 3a+r1=7c+r39r2-8r1+15d?r3 (mod 7)=7c+r3k=3a+1 k=3a+1

a=3(r2-r1) + 5d d = 15(r3-9r2+8r1)+7p, где p целое

d?15(r3-9r2+8r1) (mod 7) a = 3(r2-r1) + 5d

k=9r2-8r1+15d k = 225r3-1792r1-2016r2+105p

Ответы: 86; k=225r3-1792r1-2016r2+105p.

Итак, нами получена формула для k. Но в ней помимо r1,r2,r3 присутствует целочисленноеd. Возникает закономерный вопрос: всегда ли числоkбудет определяться единственным образом, если оно меньше 100? Меньше 150? 43? и так далее.

Китайская теорема об остатках

Китайская теорема об остатках (КТО) — несколько связанных утверждений, сформулированных в трактате китайского математика Сунь Цзы (IIIв.н.э.) и обобщенных ЦиньЦзюшао(XVIIIв.н.э.) в его книге «Математические рассуждения в 9 главах». Звучит она так:

Пусть числа M1 , M2, …, Mk — попарно взаимно простые, и M= M1*M2*…*Mk .Тогдасистема

x?B1 (modM1)? B2 (modM2)

имеет единственное решение среди чисел <0,1,…,M-1>.

Проще говоря, ответ будет всегда однозначным, если искомое число туристов меньше произведения делителей, на которые его делят. Возвращаясь к задаче № 4, мы говорим, что их будет возможно сосчитать, если их общее число не будет превышать 104. (М-1=3*5*7-1=104). Так значит, что бы посчитать человек, отталкиваясь от нашей формулы необходимо вычислить 225r3-1792r1-2016r2, а потом отнимать от него число 105 до тех пор, пока мы не получим число меньшее 105, но большее 0. Это долго и неудобно. Да и, честно говоря, число около ста человек можно сосчитать и не используя такие сложные алгоритмы.

Простейшие нелинейные диофантовы уравнения

Диофант полностью проанализировал неопределённые уравнения второй степени с двумя неизвестными. Для решения уравнений и систем более высоких степеней он разработал ещё более тонкие и сложные методы, которые привлекали внимание многих европейских математиков Нового времени. Но практически все уравнения этого типа в рамках школьного курса решаются методом разложения на множители.

Пример № 2: Решить в целых числах уравнениеx2-3xy+2y2=7.

Очевидно, что мы можем получить число 7 следующими способами: 1*7=7;7*1=7;-1*(-7)=7;-7*(-1).

Тогда составим и решим систему уравнений:

x-2y=1 x=13y=7y=6y=7 x=-5y=1 y=-6y=-1 x=-13y=-7 y=-6y=-7 x=5y=-1 y=6

Пример № 3:Доказать, что уравнение x5+3x4y- 5x3y2-15x2y3 + 4xy4+12y5=33 не имеет целочисленных корней.

Если у=0, тогда исходное уравнение примет вид x5=33. Тогда x не является целым. Значит, при у=0 данное уравнение не имеет целых решений. Если, y?0, то все пять множителей в левой части уравнения различны. С другой стороны число 33 можно представить в виде произведения максимум четырёх различных множителей (33=1·3·11 или 33=-1·3·(-11)·(-1) и т.д.). Следовательно, при y?0данное уравнение также не имеет целых решений.

Десятая проблема Гильберта

Так или иначе, возникает вопрос: любое ли диофантово уравнение можно решить, то есть найти его корни или доказать их отсутствие.

августа 1900 года состоялась II Международный конгресс математиков. На ней Давид Гильберт предложил 23 задачи. Десятая звучала так:

Пусть задано диофантово уравнение с произвольными неизвестными и целыми рациональными числовыми коэффициентами. Указать способ, при помощи которого возможно после конечного числа операций установить, разрешимо ли это уравнение в целых рациональных числах.

Множество светлых умов XX-ого века бились над этой задачей:АксельТуэ, ТуральфСкулем, Эмиль Пост, Джулия Робинсон, Мартин Дэвис и Хилари Патнем, Мартина Дэвиса и другие. И лишь в 1970 году Юрий Матиясевич завершилдоказательство алгоритмической неразрешимости этой задачи.

Давид Гильберт (23 января 1862 — 14 февраля 1943) — немецкий математик-универсал, внёс значительный вклад в развитие многих областей математики. В 1910-1920-е годы (после смерти Анри Пуанкаре) был признанным мировым лидером математиков. В 1970 г. Международный астрономический союз присвоил имя Гильберта кратеру на обратной стороне Луны.

Юрий Владимирович Матиясевич (родился 2 марта 1947 года, Ленинград) — советский и российский математик, исследователь Санкт-Петербургского отделения Математического института им. В. А. Стеклова РАН, член экспертной комиссии РСОШ по математике, академик Российской академии наук, доктор физико-математических наук

диофант уравнение математический

Эта тема многогранна и практически необъятна. Недаром над ней ломали голову ученые с мировым именем на протяжении все истории развития математики. Она затрагивает фундаментальные понятия в математике и знания о диофантовых уравнениях, как мне кажется, никогда не будут исчерпывающими.

Делая этот реферат я овладел методом рассеивания, научился решать системы уравнений на задачи про остатки, познакомился с историей освоения методов решения диофантовых уравнений.

По миру математики, которая уже давно мудра и величава, мы идём проторенным путём.

Но каждый может стать первооткрывателем: вначале для себя, а в будущем, может, и для других…

Я думаю продолжить работу над этой темой, расширить свои познания в решении неопределённых уравнений. Изучение новых методов решения обогащает багаж знаний любого человека, тем более, что они могут оказаться актуальными на ЕГЭ (С6).

Список используемой литературы

1.Журнал «Квант» 1970г. №7

.«Энциклопедия юного математика» 520 с.

Пичугин Л.Ф. «За страницами учебника алгебры», М., 1990г., 224с.

Глейзер Г.И. «История математики в школе 10-11», 351с

Петраков И.А. «Математика для любознательных», М., 2000г. 256с.

Репетиторство

Нужна помощь по изучению какой-либы темы?

Наши специалисты проконсультируют или окажут репетиторские услуги по интересующей вас тематике.
Отправь заявку с указанием темы прямо сейчас, чтобы узнать о возможности получения консультации.

Методы решения диофантовых уравнений.

ученик 8 А класса Трухин Николай (14 лет)

В 2011-2012 году я выполнял исследовательскую работу на тему: «Решение уравнений в Древней Греции и Индии». При работе над ней я познакомился с трудами Диофанта Александрийского и Мухаммеда аль — Хорезми. В своей прошлой работе я рассмотрел некоторые способы решения уравнений первой степени с двумя неизвестными, познакомился с некоторыми старинными задачами, приводящими к решению уравнений первой степени с двумя неизвестными.

Мухаммед Бен Мусса аль – Хорезми, — или Магомед сын Моисея Хорезмского, состоящий членом «дома мудрости» в Иране, около 820 года нашего летоисчисления написал книгу, где учил решать простые и сложные вопросы арифметики, которые необходимы людям при дележе наследства, составлении завещаний, разделе имущества и судебных делах, в торговле, всевозможных сделках. С именем аль – Хорезми связаны понятия «алгебра», «арабские цифры», «алгоритм». Он отделил алгебру от геометрии, внёс большой вклад в математику исламского средневековья. Мухаммед аль – Хорезми был известен и уважаем, как при жизни, так и после смерти.

Но мне захотелось больше узнать о Диофанте. И тема моего исследования в этом году: « Методы решения диофантовых уравнений»

Диофант Александрийский — один из самых своеобразных древнегреческих математиков, труды которого имели большое значение для алгебры и теории чисел. Из работ Диофанта самой важной является «Арифметика», из 13 книг которой, только 6 сохранились до наших дней. В сохранившихся книгах содержится 189 задач с решениями. В первой книги изложены задачи, приводящиеся к определенным уравнениям первой и второй степени. Остальные пять книг содержат в основном неопределенные уравнения (неопределенными называются уравнения, содержащие более чем одно неизвестное). В этих книгах ещё нет систематической теории неопределённых уравнений, методы решения меняются от случая к случаю. Диофант довольствуется одним решением, целым или дробным, лишь бы оно было положительным. Тем не менее, методы решения неопределённых уравнений, составляют основной вклад Диофанта в математику. В символике Диофанта был один только знак для неизвестного. Решая неопределённые уравнения, он применял в качестве нескольких неизвестных произвольные числа, вместо которых можно было взять и любые другие, что и сохраняло характер общности его решений.

Цель моей работы:

1.Продолжить знакомство с диофантовыми уравнениями.

2.Исследовать методы перебора и рассеивания (измельчения) при решении диофантовых уравнений.

3.Исследовать возможность применения диофантовых уравнений для решения некоторых практических задач.

II . Обзор литературы.

При написании работы мной использовалась следующая литература:

Мной использована информация о Диофанте и аль – Хорезми.

Книга посвящена методам Диофанта при решении неопределённых уравнений. В ней рассказывается о жизни и самого Диофанта. Эта информация использована мной в работе.

В книги рассказывается об истории алгебры с древних времён. Я использовал информацию о теории уравнений, начиная с древности.

В этой книге собрано около 200 статей, посвященных основным понятиям математики и её приложения. Мной были использованы материалы статей «Алгебра», «Уравнения», «Диофантовы уравнения»

Из книги взяты тексты задач для практического использования.

По теме мной использовался сайт:

http :// ru . wikipedia . org (информация об аль – Хорезми и Диофанте. О методах решения диофантовых уравнений).

В наши дни каждый, кто занимался математикой, слышал о диофантовых уравнениях. Алгебраические уравнения с целыми коэффициентами, решаемые во множестве целых (реже рациональных) чисел, вошли в историю математики как диофантовы. Наиболее изучены диофантовы уравнения 1 и 2 степени. В содержании моей работы включены задачи, которые сводятся к решению уравнения первой степени с двумя неизвестными

Задача 1. В клетке находится x фазанов и у кроликов. Сколько в клетке фазанов и кроликов, если общее количество ног равно 62.

Общее число ног можно записать с помощью уравнения 2х+4у=62 (2)

Это равенство, которое я составил по условию задачи, называют уравнением с двумя переменными. Данное уравнение называют линейным уравнением. Линейные уравнения играют важную роль при решении различных задач. Напомню основные положения, связанные с этим понятием.

Линейным уравнением с двумя переменными называется уравнение вида ax +by =c , где x и у – переменные, а, b и с – некоторые числа.

Однозначно определить из уравнения (2) значения x и y нельзя. Даже если ограничиться только натуральными значениями переменных, здесь могут быть такие случаи: 1 и 15, 3 и 14, 5 и 13 и т. д.

Пара чисел ( a , b ) называется решением уравнения с двумя переменными, если при замене x на а и y на b получаем истинное равенство.

Каждому уравнению с двумя переменными соответствует множество его решений, т. е. множество, состоящее из всех пар чисел (a , b ), при подстановке которых в уравнение получается истинное равенство. При этом, конечно, если заранее указаны множества Х и Y , которые могут принимать неизвестные x и у, то надо брать лишь такие пары (a , b ), для которых а принадлежит Х и b принадлежит Y .

Пару чисел ( a , b ) можно изобразить на плоскости точкой М, имеющей координаты а и b , М= М (a , b ). Рассматривая изображения всех точек множества решений уравнения с двумя неизвестными, получим некоторое подмножество плоскости. Его называют графиком уравнения.

Можно доказать, что графиком линейного уравнения с двумя переменными, в котором хотя бы один из коэффициентов не равен нулю, является прямая линия. Для построения графика этого уравнения достаточно взять две точки с координатами и провести через них прямую. Графический метод решения я использовал в предыдущей работе.

Два уравнения с двумя переменными, имеющие одни и те же решения называются равносильными.

Например, равносильны уравнения х+2у=5 и 3х+6у=15 – любая пара чисел, удовлетворяющая одному из этих уравнений, удовлетворяет и второму.

Уравнения с двумя переменными обладают такими же свойствами, как и уравнения с одной переменной:

1) если в уравнении перенести слагаемое из одной части в другую, изменив его знак, то получится уравнение, равносильное данному;

2) если обе части уравнения умножить или разделить на одно и то же отличное от нуля число, то получится уравнение, равносильное данному.

Существует несколько способов решения диофантовых уравнений:

Метод перебора вариантов

Использование алгоритма Евклида

С использованием цепной дроби

Метод рассеивания (измельчения)

При помощи программирования на языке программирования Паскаль

В своей работе я исследовал методы – перебор вариантов и рассеивание (измельчения)

Рассматривая способ перебора вариантов, необходимо учитывать количество возможных решений уравнения. Например, этот способ можно применить, решая следующую задачу:

Задача 2 . Андрей работает летом в кафе. За каждый час ему платят 10 р. И высчитывают 2 р. за каждую разбитую тарелку. На прошедшей неделе он заработал 180 р. Определите, сколько часов он работал и сколько разбил тарелок, если известно, что он работает не более 3 ч в день.

Пусть x часов он всего работал в неделю, тогда 10х р. ему заплатили, но он разбил у тарелок, и с него вычли 2у р. Имеем уравнение 10х – 2у =180 , причем x меньше или равен 21. Получим: 5х-у=90, 5х=90+у, х=18+у:5.

Так как x целое число, то у должно нацело делится на 5, чтобы в правой части получилось целое число. Возможны четыре случая

у=0, х=18, т. е. решением является пара – (18, 0);

Эту задачу я решил, используя способ перебора вариантов. Ответ содержит четыре возможных варианта. Я попробовал решить этим способом ещё несколько задач.

Задача 3. Из двухрублевых и пятирублевых монет составлена сумма в 23 рубля. Сколько среди этих монет двухрублевых?

Пусть x – количество двухрублевых монет, у – количество пятирублевых монет. Составим и решим уравнение: 2х+5у=23; 2х=23–5у; x = (23 – 5у):2; x =(22+1 – 5у):2, почленно поделим 22 на 2 и (1 – 5у) на 2, получим: x = 11 + (1 – 5у):2.

Так как x и y натуральные числа по условию задачи, то левая часть уравнения есть натуральное число, значит, и правая часть должна быть натуральным числом. К тому же, чтобы получить в правой части число натуральное, нужно чтобы выражение (1 – 5у) нацело делилось на 2. Осуществим перебор вариантов.

y =1, х=9, то есть двухрублевых монет может быть 9;

у=2, при этом выражение (1 – 5у) не делится нацело на 2;

у=3, х=4, то есть двухрублевых монет может быть 4;

при у больше или равном 4 значение x не является числом натуральным.

Таким образом, ответ в задаче следующий: среди монет 9 или 4 двухрублевых.

Задача 4. Шехерезада рассказывает свои сказки великому правителю. Всего она должна рассказать 1001 сказку. Сколько ночей потребуется Шехерезаде, чтобы рассказать все свои сказки, если x ночей она будет рассказывать по 3 сказки, а остальные сказки по 5 за у ночей

Сказочнице потребуется x + у ночей, где x и у – натуральные корни уравнения 3х+5у=1001

x = (1001 – 5у):3; так как x – натуральное число, то и в правой части равенства также должно быть натуральное число, а значит выражение (1001 – 5у) должно нацело делиться на 3.

Осуществим перебор вариантов.

у=1, 1001 – 5у=1001-5= 996, 996 делится на 3, следовательно, х=332; решение (332;1);

у=2, 1001– 10=991, 991 не делится на 3;

у=3, 1001 – 15 = 986; 986 не делится на3;

у =4, 1001 – 20 = 981, 981 делится на 3, следовательно, x = 327, решение (327;4) и т. д.

В этой задаче существует 67 пар возможных корней, я не стал показывать все решения данной задачи, т. к. это занимает много времени.

Уравнение ax + by = c (1) в приведённых задачах я решал способом перебора вариантов. Я уяснил для себя, что способ перебора вариантов не всегда эффективен для решения данной задач, так как для нахождения всех решений уравнения требуются значительные временные затраты. И, на мой взгляд, в настоящее время он неактуален.

Поэтому я решил задачу про Шехерезаду, используя метод рассеивания (измельчения).

Метод рассеивания – это общий метод для решения в целых числах неопределённых уравнений первой степени с целыми коэффициентами.

Итак, решим задачу про Шехерезаду методом рассеивания:

Обратимся к уравнению 3х + 5у = 1001.

Перепишем его иначе: 3х= 1001- 5у; 3х= 1001 — 2у — 3у;

x = – y +
и обозначим x l = у + x

В результате уравнение примет вид 3х 1 = 1001 – 2у или

у = – x l
.

Если вновь произвести замену у 1 = у + х 1 , то придем к уравнению

x 1 + 2у 1 = 1001. Заметим, что коэффициенты при неизвестных уменьшились — измельчились.

Здесь коэффициент при x 1 , равен 1, а поэтому при любом целом у 1 = t число х 1 тоже целое. Остается выразить исходные переменные через t :

х 1 = 1001 – 2 t , следовательно, у = – 1001 + 3 t , а x = 2002 – 5 t . Итак, получаем бесконечную последовательность (2002 – 5 t , – 1001 + 3 t ) целочисленных решений. Внешний вид формул для нахождения значений переменных отличается от решений, полученных ранее, но с учетом условия задачи, корни получаются те же самые. Так, пара (332;1) получается при t =334.

На мой взгляд, этот метод не только более удобный (у него есть алгоритм действий), но и интересный. Известно, что этот метод в первые применил в начале VI в. индийский математик Ариабхатта.

В прошлом году я показывал решение древней индийской задачи Брахмагупты методам рассеивания, которое предложил сам Брахмагупта. Решение было нерациональным.

Оно представлено ниже:

«Найти два целых числа, зная, что разность произведений первого на 19 и второго на 8 равно 13. »

В задаче требуется найти все целые решения уравнений.

Выражаю y – неизвестное с наименьшим по абсолютной величине коэффициентом через x , получаю:

Нужно теперь узнать, при каких целых значениях x соответствующие значения y являются тоже целыми числами. Перепишу уравнение (2) следующим образом:

Из (3) следует, что y при целом x принимает целое значение только в том случае, если выражение (3x -13)/8 является целым числом, скажем y 1 . Полагая

вопрос сводится к решению в целых числах уравнения (4) с двумя неизвестными x и y 1 ; его можно записать так:

Это уравнение имеет по сравнению с первоначальным (1) преимущество, что 3 – наименьшее из абсолютных величин коэффициентов при неизвестных – меньше, чем в (1), т.е. 8. Это было достигнуто благодаря тому, что коэффициент при x (19) был заменен остатком от деления на 8.

Продолжая тем же способом, мы получим из (5):

Итак, неизвестное x при целом y 1 только тогда принимает целые значения, когда (2y 1 + 13)/3 есть целое число, скажем y 2 :

Это самое простое из всех рассмотренных неопределенных уравнений, так как один из коэффициентов равен 1.

Отсюда видно, что y 2 принимают целые значения при любых целых значениях y 3 . Из равенств (6), (9), (12), (3) путем последовательных подстановок можно найти следующие выражения для неизвестных x и y уравнения (1):

Таким образом, формулы

При y 3 = 0, + 1,+ 2, + 3, … дают все целые решения уравнения (1).

В следующей таблице приведены примеры таких решений.

Решим эту задачу рационально. В решении используется определённый алгоритм.

Найти два числа, если разность произведений первого на 19 и второго на 8 равна 13.

Решение. Требуется решить уравнение 19х — 8у = 13

Перепишем его иначе: 8y =19x –13; 8y =16x +3x –13; у = 2х +

и обозначим y 1 = у — 2х.

В результате уравнение примет вид 8у 1 = Зx — 13 или x = 2y 1
.

Если вновь произвести замену х 1 = x — 2у 1 , то придем к уравнению

3 x l — 2у 1 = 13.

Коэффициенты при неизвестных уменьшились — измельчились. Дальнейшее измельчение: y 1 = x l +
, то получим у 2 =у 1 –х 1 .

В результате последнее уравнение преобразуется к виду х 1 — 2у 2: = 13. Здесь коэффициент при х 1 , равен 1, а поэтому при любом целом у 2 = t число х 1 тоже целое.

Остается выразить исходные переменные через t :

вначале выразим х 1 =2t +13, y 1 = 3t +13; а затем x = 8 t +39, y = 19 t + 91.

Итак, получаем бесконечную последовательность (39 + 8 t , 91 + 19 t ) целочисленных решений . Уравнение ax + by = c (1) в приведённых задачах я решал способом рассеивания (измельчения).

Изучая диофантовы уравнения для их решения, я использовал методы перебора вариантов и рассеивания (измельчения). Этими методами я решал, как современные, так и древние задачи. В содержании моей работы были включены задачи, которые сводятся к решению уравнений первой степени с двумя переменными ах+b у=с (1)

В ходе своей работы я сделал выводы:

Метод перебора требует значительные временные затраты, а значит он не очень удобен и рационален.

Более рациональным, на мой взгляд, является метод рассеивания. Когда я решал старинную индийскую задачу этим методом, я понял, что существует определённый алгоритм решения. Мне было достаточно полученных в школе знаний. Я убедился, что методы решения дофантовых уравнений с развитием математики постоянно совершенствуются.

На следующий год я хочу продолжить изучение методов решения диофантовых уравнений.

V . Список литературы

Г. И. Глейзер «История математики в школе» М.: изд. «Просвещение» 1964г. 376с.

И. Г. Башмакова «Диофант и диофантовы уравнения» М.: изд. «Наука» 1972г. 68с.

В. А. Никифоровский «В мире уравнений» М.: изд. «Наука» 1987г. 176с.

А. П. Савин «Энциклопедический словарь юного математика» М.: изд. «Педагогика» 1985г.

Г. М. Возняк, В. Ф. Гусев «Прикладные задачи на экстремумы» М.: изд. «Просвещение» 1985г. 144с.

На фермерском хозяйстве нужно провести водопровод длиной 167м. Имеются трубы длиной 5м и 7м. Сколько нужно использовать тех и других труб, чтобы сделать наименьшее количество соединений (трубы не резать)?

Учитывая, что количество как одних, так и других труб может изменяться, количество 7 – метровые трубы обозначаем через х, 5 – метровые – через у

Тогда 7х – длина 7 – метровых труб, 5у – длина 5 – метровых труб.

Отсюда получаем неопределённое уравнение:

Выпазив, например, переменную у через переменную х , получим:

Методом перебора легко найти соответствующие пары значений х и у , которые удовлетворяют уравнению 7х+5у=167

Из этих решений наиболее выгодное последнее, т. е. х=21; у=4.

Многие старинные способы отгадывания чисел и дат рождения основываются на решении диофантовых уравнений. Так, например, чтобы отгадать дату рождения (месяц и число) собеседника, достаточно узнать у него сумму, получаемую от сложения двух произведений: числа даты ( х ) на 12 и номера месяца ( у ) на 31.

2. Пусть сумма произведений, о которых идёт речь, равна 330. Найти дату рождения.

Решим неопределённое уравнение

С помощью метода рассеивания получим:

Ввиду ограничений, легко констатировать, что единственным решением является

Итак, дата рождения: 12-е число 6-го месяца, т.е. 12 июня.