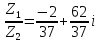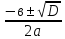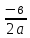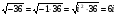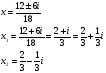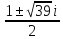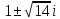Урок по алгебре и началам анализа в 10-м классе по теме «Алгебраические действия над комплексными числами»
Разделы: Математика
Цели урока:
- Образовательные – познакомить учащихся с историей комплексных чисел;
формировать навыки выполнения алгебраических действий над комплексными числами; формировать навыки пользования компьютером для выполнения обучающих и контролирующих тестов.
- Развивающие – развивать мыслительную деятельность учащихся на уроке посредством выполнения тестовых заданий;
способствовать формированию навыков самостоятельной работы и работы в мини-группе; развивать интерес к предмету через включение в план урока исторического материала и практических заданий;
развивать интерес к роли личности в становлении математической науки;
развивать творческие способности в ходе выполнения исследовательской работы.
- Воспитательные – воспитывать у учащихся способность подходить к изучаемым проблемам с позиции исследователя; воспитывать чувство личной ответственности за достижение положительных результатов при самостоятельной работе и в группе.
План урока.
- Актуализация знаний.
- Постановка цели урока.
- Решение заданий на выполнение действий с комплексными числами.
- Проведение обучающего и контрольного теста.
- Подведение итогов.
Ход урока.
| Деятельность учителя: | Деятельность учеников: |
| Организационный момент. Учитель приветствует учащихся. | Учащиеся проверяют готовность к уроку, анализируют свое психологическое состояние. |
| Вводное слово учителя (презентация) | |
| Постановка проблемы. Какие задачи исторически привели к введению комплексных чисел? | Отчет учащихся о своей исследовательской работе (демонстрация сайтов). |
| Какие же числа называются комплексными и как выполнять с ними алгебраические действия? (Презентация) | Выполнение серии задач на действия с комплексными числами (в тетради). |
| Как можно узнать результат достижения своих образовательных целей? (Тест) | Выполнение обучающего и контрольного тестов. |
| Подведение итогов урока. |
Конспект урока.
— Сегодня на уроке мы с вами продолжим знакомство с полем комплексных чисел. Тема нашего урока «Алгебраические действия над комплексными числами». (Презентация, слайды 1-4).
— «Комплексное число – это тонкое и поразительное средство божественного духа, почти амфибия между бытием и небытием». Писал Лейбниц Готфрид Вильгельм (1.7.1646 — 14.11.1716) — немецкий математик, физик и философ, организатор и первый президент Берлинской АН (1700), чл. Лондонского королевского общества (1673), чл. Парижской АН (1700).
— Мы с вами на уроке попытаемся снять дух мистики, привнесенный Лейбницем, да и другими математиками, в математическую науку, и не только осознаем необходимость введения комплексных чисел для решения многих задач, но и будем выполнять с ними алгебраические действия: сложение, вычитание, умножение и деление.
— Многовековая история развития представлений человека о числах — одна из самых ярких страниц развития человеческой культуры. В стремлении расширить мир чисел трудноразгадываемым образом переплелись разнообразные мотивы.
— Дроби появились очень рано – уже у египтян и вавилонян – по-видимому, в связи с переходом к более мелким единицам измерения. Их связь с делением натуральных чисел понималась более смутно и вторично.
— Греки осознавали числа через процесс геометрического измерения: именно так они себе уяснили существование иррациональных чисел (несоизмеримость диагонали квадрата и его стороны) и построили теорию «величины» (как мы сказали бы сегодня, теорию положительных действительных чисел).
— Отрицательные числа появились в 5-6 веках в индийской и арабской математике, где на первый план выдвинулась вычислительная сторона дела. При этом вычислители рассматривали отрицательные числа как «воображаемые», ненастоящие числа, которыми удобно пользоваться в промежуточных вычислениях как результатом вычитания, когда оно невыполнимо в области положительных чисел. Ни о каком равноправии отрицательных чисел с положительными речь не шла: в окончательном ответе, кроме простейших ситуаций, отрицательные числа не появлялись. Об отношении к ним выразительно говорят разные варианты их названий: «ложные», «фиктивные», «абсурдные», «невозможные», «мнимые».
— Впрочем, последний термин позднее пришлось «уступить» другому классу чисел, который удивительным образом появился в европейской математике одновременно с первым серьезным рассмотрением отрицательных чисел.
— Восстановить историческую картину нам помогут ученицы, которые, готовясь к школьной научно-практической конференции, были вынуждены для раскрытия своих тем повторить исторические шаги в развитии представления о числе и познакомиться с понятием комплексного числа. (Выступления учениц).
— Итак, наши представления о числах стали более широкими. И теперь для нас не будет проблемой решения любого квадратного или кубического уравнения. Но для этого нужно научиться грамотно выполнять действия с комплексными числами.
— Вспомним основные правила для выполнения алгебраических действий над комплексными числами.
— Действия над комплексными числами в алгебраической форме. (Презентация, слайды 5-8).
— Сложение, вычитание, умножение комплексных чисел в алгебраической форме производят по правилам соответствующих действий над многочленами.
Решение.
(здесь учтено, что i 2 = – 1).
Замечание. При выполнении умножения можно использовать формулы:
Пример. Выполнить действия:
Решение.
б) (3 – 5i) 2 = 9 – 2×3×5i + 25i 2 = 9 – 30i – 25 = – 16 – 30i;
Комплексные числа
План — коспект урока по теме «Комплексные числа»
Просмотр содержимого документа
«Комплексные числа»
Комплексные числа и квадратные уравнения.
10 класс ( профильный уровень).
«Мысль выражать все числа знаками
настолько проста, что именно из-за
этой простоты сложно осознать,
сколь она удивительна»
Пьер Симон Лаплас
формирование у школьников различных приёмов мыслительной деятельности;
включение новой информации в структуру прежних знаний;
расширить сведения учащихся о числах;
привитие интереса к предмету;
формирование уверенности в своих знаниях.
воспитание чувства ответственности.
развитие эмоционально-положительного отношения к изучению математики.
Обобщить и систематизировать знания, умения и навыки учащихся по теме урока.
Развивать умения применять теоретические знания при решении заданий; умение анализировать, сравнивать, обобщать, устанавливать причинно-следственные связи; классифицировать.
Формировать навыки самостоятельной деятельности
Учебно-методическая карта фрагмента урока
Методы и методические приемы
Умение слушать, настраиваться на урок
Мотивация и целеполагание. Активизация деятельности.
Определение целей урока
Принятие целей урока
Умение синтезировать данные
Тест (для слабых)
( проверка через документ камеру)
Умение осознавать основное содержания темы
Умение использовать полученные знания
Умение синтезировать данные
Сообщение новых знаний
Решение квадратных уравнений на множестве комплексных чисел.
Организация взаимосвязи своих знаний и их применение.
Этап обобщения и систематизации
Индивидуальная работа. (слайд 9-10)
Взаимооценка (проверка по слайду)
Умение проявлять гибкость, оказавшись в нестандартных ситуациях
Умение организовывать взаимосвязь своих знаний и упорядочивать их
Умение принимать решения и брать на себя ответственность за их последствия
Задания различного уровня сложности
Поиск, анализ и отбор необходимой информации, ее преобразование, сохранение и передача
Ответы на вопросы
Умение выделять главное
Качественная характеристика работы учащихся
На прошлых уроках мы познакомились с понятием комплексного числа, алгебраической формой записи комплексного числа, научились выполнять различные действиями над комплексными числами, научились находить модуль и аргумент комплексного числа.
Работа в парах — решение кроссворда (историческая справка), для слабых тестирование. (проверка)
Индивидуальная работа. Заполняют лист само оценивания.
1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное.
Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное.
4.
4. 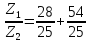
Решите квадратные уравнения:
х 2 – 5х + 6=0 х 2 +6х+9=0 9х 2 -12х + 5 = 0
Решение квадратных уравнений в поле комплексных чисел
1 cлучай: D0, 2 корня, х1,2 =
2 случай D=0, 1 коре нь, х1,2 =
3 cлучай: D1,2 =
Сколько корней может иметь записанное на доске квадратное уравнение?
У доски решает ученик:
D= 144-180= -36, считаем, что
-Теперь вы можете блеснуть эрудицией, услышав, что при D
— Вот и сделали мы шаг в глубину математического айсберга. Комплексные числа широко применяются в электротехнике, в аэродинамике. Отец русской авиации, Н.Г. Жуковский использовал их при разработке теории крыла самолета. Возможно, они пригодились для получения промежуточного результата.
x 2 – 4x + 13 = 0.
9 x 2 + 12x + 29 = 0.
1. Решите уравнение x 2 – 4x + 5 = 0.
Решение. D = – 4 уравнение имеет мнимые корни: 2+i, 2-i
2. Решите уравнение x 2 – x + 10 = 0.
Решение. D = – 39 , уравнение имеет мнимые корни:
3. Решите уравнение x 2 – 4x + 13 = 0.
Решение. D = – 36 уравнение имеет мнимые корни: 2+3i, 2-3i
4. Решите уравнение x 2 – 2x + 15 = 0.
Решение. D = – 56 , уравнение имеет мнимые корни:
А как бы вы решили следующее квадратное уравнение?
х 2 + (5 – 2i) x + 5(1– i) = 0;.
Вот над этой проблемой будем работать на следующем уроке, а желающие могут попробовать самостоятельно попробовать свои силы.
Домашнее задание п.35 №7-8(а, б),10.
Спасибо за урок!
1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное.
2. Проверьте правильность следующих утверждений:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.
Для проверки возьмите числа: Z1=2i, Z2=-3i
б) Произведение двух чисто мнимых чисел равно действительному числу.
Для проверки возьмите числа: Z1=-5i, Z2=3i
в) Квадрат чисто мнимого числа равен действительному отрицательному числу.
Для проверки возьмите числа: Z1=10i
г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.
Для проверки возьмите числа: Z1=7i, Z2=3
которых равны 2.
Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное.
2. Проверьте правильность следующих утверждений:
а) Сумма и разность чисто мнимых чисел есть чисто мнимое число.
Для проверки возьмите числа: Z1=2i, Z2=-3i
б) Произведение двух чисто мнимых чисел равно действительному числу.
Для проверки возьмите числа: Z1=-5i, Z2=3i
в) Квадрат чисто мнимого числа равен действительному отрицательному числу.
Для проверки возьмите числа: Z1=10i
г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу.
Для проверки возьмите числа: Z1=7i, Z2=3
1. Решите уравнение x 2 – 4x + 5 = 0. 2+i, 2-i
2. Решите уравнение x 2 – x + 10 = 0.
3. Решите уравнение x 2 – 4x + 13 = 0. 2+3i, 2-3i
4. Решите уравнение x 2 – 2x + 15 = 0.
1. Решите уравнение x 2 – 4x + 5 = 0. 2+i, 2-i
2. Решите уравнение x 2 – x + 10 = 0.
3. Решите уравнение x 2 – 4x + 13 = 0. 2+3i, 2-3i
4. Решите уравнение x 2 – 2x + 15 = 0.
Решение уравнений с комплексными числами
Итак, необходимо решить уравнение с комплексными переменными, найти корни этого уравнения. Рассмотрим принцип решения комплексных уравнений, научимся извлекать корень из комплексного числа.
Для того, чтобы решить уравнение n-й степени с комплексными числами, используем общую формулу:

где |z| — модуль числа, φ = arg z — главное значение аргумента, n — степень корня, k — параметр, принимает значения : k = <0, 1, 2, 3, …n-1 >.
Пример 1. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня третьей степени из комплексного числа
Воспользуемся общей формулой для вычисления корней степени n комплексного числа z. Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения.
Пример 2. Найти все корни уравнения
Найдем дискриминант уравнения:

Поскольку дискриминант отрицательный, уравнение имеет два комплексно-сопряженных корня. Вычислим корень из дискриминанта:
Найдем корни уравнения:

Ответ:
Пример 3. Найти все корни уравнения
Выразим z из уравнения:
Все корни заданного уравнения являются значениями корня четвертой степени из комплексного числа
Вновь используем общую формулу для нахождения корней уравнения n степени комплексного числа z.
n = 4 — количество корней данного уравнения. k = <0, 1, 2, 3>. Найдем модуль комплексного числа:
Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2, 3 найдем все 4 корня уравнения:
Пример 4. Найти корни уравнения

Решение кубического уравнения комплексными числами:
Воспользуемся общей формулой для вычисления корней степени 3 комплексного числа z.
Найдем все необходимые значения для формулы:

Подставим найденные значения в формулу:
Последовательно подставляя вместо k значения 0, 1, 2 найдем три корня исходного уравнения:
Домашнее задание: Самостоятельно составить и решить уравнение с комплексными числами.
Условия: переменная z должна быть «спрятана» и представлена в качестве аргумента тригонометрической функции косинуса. Чтобы привести данное уравнение к привычной форме, нужно «вытащить» z, а для этого необходимо помнить, как решаются тригонометрические уравнения,а также знать, как применять свойства логарифмической функции от комплексного числа.
После того, как мы решили тригонометрическое уравнение с комплексным числом, получаем «голый» z, который представлен в качестве аргумента обратной тригонометрической функции. Чтобы преобразовать данное выражение, нужно использовать формулу разложения арккосинуса в логарифм.
Вместо z — выражение (3i/4) и дальше все делаем по приведенной выше формуле, преобразовывая выражение под корнем, используя свойства мнимой единицы i.
Как быть далее? Теперь будем использовать формулу для решения выражения с натуральным логарифмом.
Для того чтобы найти корни логарифмического уравнения, нужно найти модуль комплексного числа |z| и его аргумент φ = arg z. По сути, перед нами чисто мнимое число.
Теперь предлагаем ознакомиться с формулами, которые могут пригодиться при решении уравнений или неравенств с комплексными числами. Это формулы, где комплексное число выступает в роли аргумента тригонометрической функции, логарифмической функции или показательной функции.
http://multiurok.ru/index.php/files/kompleksnye-chisla.html
http://matematyka.ru/reshenie-uravnenij-s-kompleksny-mi-chislami/