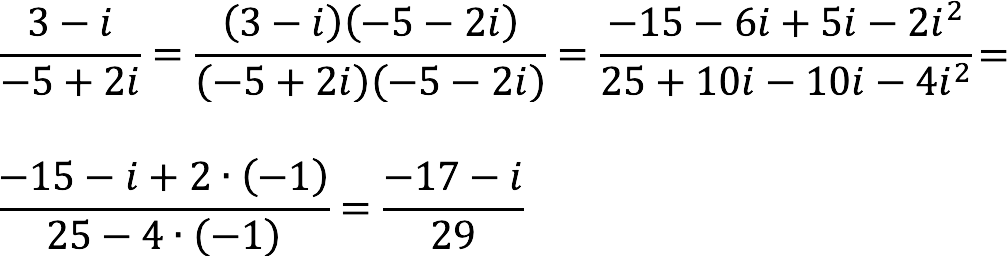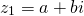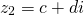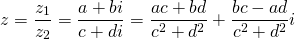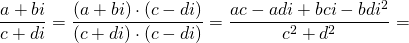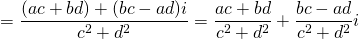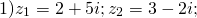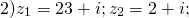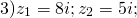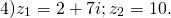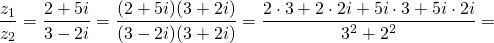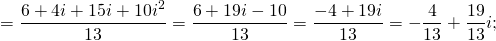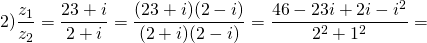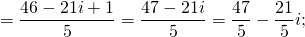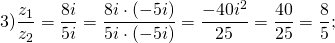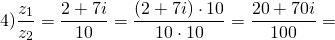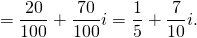Как решать комплексные уравнения деление

Деление комплексных чисел

В данной публикации мы рассмотрим формулы, с помощью которых можно найти частное двух комплексных чисел, представленных в алгебраической или тригонометрической форме. Также приведены примеры для лучшего понимания теоретического материала.

Деление в алгебраической форме

Результатом деления (т.е. частное) двух комплексных чисел и также является комплексное число z :

Порядок действий следующий:

Делимое и делитель умножаем на число, комплексно сопряженное делителю. Не забываем, что .

Примечание: Для комплексно сопряженным будет число , т.е. действительная часть остается той же, а у мнимой знак меняется на противоположный.

Пример 1:
Разделим комплексное число на .

Решение:
Руководствуемся планом действий, описанным выше, и получаем:

Деление в геометрической форме

Если комплексные числа заданы в тригонометрической форме, например, и , то разделить их можно по формуле ниже:

Пример 2
Найдем частное комплексных чисел: и .

Деление комплексных чисел

Деление комплексных чисел в алгебраической форме

Частным двух комплексных чисел $z_<1>=a_<1>+b_ <1>i$ и $z_<2>=a_<2>+b_ <2>i$ называется число $z$, которое задается соотношением:

На практике деление комплексных чисел проводят по следующей схеме:

1. сначала делимое и делитель умножают на число, комплексно сопряженное делителю, после чего делитель становится действительным числом;
2. в числителе умножают два комплексных числа;
3. полученную дробь почленно делят.

Задание. Найти частное $\frac<-2+i><1-i>$

Решение. Домножим и числитель, и знаменатель заданной дроби на число, комплексно сопряженное к знаменателю $1-i$, это будет $1+i$, тогда имеем:

Далее перемножаем комплексные числа как алгебраические двучлены, учитывая, что $i^<2>=-1$:

Деление комплексных чисел в геометрической форме

Если надо поделить комплексные числа $z_<1>$ и $z_<2>$ в геометрической форме: $\frac>>=\frac<\left|z_<1>\right|\left(\cos \phi_<1>+i \sin \phi_<1>\right)><\left|z_<2>\right|\left(\cos \phi_<2>+i \sin \phi_<2>\right)>$ , то искомое число

То есть модуль частного двух комплексных чисел равен частному модулей, а аргумент — разности аргументов делимого и делителя.

Деление комплексных чисел

Деление комплексных чисел определяется как действие, обратное умножению.

Частным двух комплексных чисел z1 и z2≠0 называется комплексное число z , при умножении которого на z2 получается z1:

Для комплексных чисел, записанных в алгебраической форме:

На практике частное комплексных чисел находят умножением делимого и делителя на число, комплексно-сопряженное делителю.

С помощью формулы правило деления комплексных можно записать так:

Найти частное комплексных чисел:

1) Чтобы выполнить деление комплексных чисел, записанных в алгебраической форме, и делимое, и делитель умножаем на число, комплексно-сопряженное делителю (вариант: и числитель, и знаменатель умножаем на число, сопряженное знаменателю):

Умножение комплексных чисел выполняем как умножение многочленов.

i² заменяем на -1.

Деление комплексных чисел, представленных в тригонометрической форме, будет рассмотрено позже.