Как решать квадратные уравнения способом группировки

Как решать квадратные уравнения способом группировки

7.Решение уравнений с использованием свойств коэффициентов

Таким образом, ясно, что при решении квадратных уравнений учащиеся нашей школы используют традиционно формулы дискриминанта и корней уравнения, что требует громоздких вычислений и как следствие больших затрат времени, что непозволительно в процессе сдачи экзаменов.

Проблемный вопрос: существуют ли кроме общепринятых приемов решения квадратных уравнений другие, которые позволяют быстро и рационально решать квадратные уравнения? Какие существуют рациональные способы решения квадратных уравнений?

Гипотеза: установление связи между коэффициентами и корнями квадратного уравнения позволит найти эффективные приемы быстрого решения квадратного уравнения.

Цель: установив связь между коэффициентами и корнями квадратного уравнения, найти новые рациональные приемы решения уравнений.

Задачи:

1.Изучить литературу по истории приемов решения квадратных уравнений

2. Обобщить накопленные знания о квадратных уравнениях и способах их решения.

3. Установить зависимость корней квадратного уравнения от его коэффициентов и найти эффективные приемы быстрого решения квадратного уравнения, в том числе с большими коэффициентами.

4.Изложить наиболее известные способы решения квадратных уравнений.

3.Показать нестандартные способы решения квадратных уравнений. Сделать выводы.

5. Разработать дидактический материал для проведения практикума по решению квадратных уравнений с использованием новых приемов в помощь ученикам, увлеченным математикой.

Объект исследования: квадратные уравнения

Предмет исследования: методы и приемы решения квадратных уравнений, в том числе с большими коэффициентами

Актуальность темы: тема «Квадратные уравнения» является одной из самых актуальных. Она находит широкое применение в разных разделах математики, имеет теоретическую и практическую значимость. Ведь почти все, что окружает человека так или иначе связано с математикой. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.

Тема исследования:

Нетрадиционные способы решения квадратных уравнений.

Методы исследования: анкетирование, сбор статистических данных, обработка собранных сведений и информации, оформление результатов исследования.

Итог работы.

Каждый ученик должен прийти к выводу «Мой способ решения квадратного уравнения – понятный, но я хочу найти для себя самый рациональный»

Глава 1. Историческая справка.

В те далекие времена, когда мудрецы впервые стали задумываться о равенствах, содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. «Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37. «, — поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами. Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: «Смотри!», «Делай так!», «Ты правильно нашел». В этом смысле исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.

Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово «аль-джебр» из арабского названия этого трактата – «Китаб аль-джебер валь-мукабала» («Книга о восстановлении и противопоставлении») – со временем превратилось в хорошо знакомое всем слово «алгебра», а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.

Основной материал, связанный с изучением темы «Квадратные уравнения» находится в УМК под редакцией С. А. Теляковского за 8 класс. В учебнике разобраны все основные вопросы по теме:

1. Определение и виды квадратных уравнений

2. Основные методы решения квадратных уравнений

Однако, дополнительный материал, связанный с историей вопроса о возникновении квадратных уравнений можно найти в «Энциклопедия по математике» «Занимательная математика», М., 2007. Способы решения задач на квадратные уравнения в полном объёме раскрыты в изданиях «Сборник элективных курсов» Волгоград, 2006 г. Рациональные приемы решения квадратных уравнений в полном объеме освещены на сайтах интернет.

Таким образом, изученная литература позволила приобрести новые интересные знания по истории возникновения квадратного уравнения, приобрести опыт по решению различных квадратных уравнений и перейти к следующему этапу в исследовании – перенести полученные знания в нестандартную ситуацию.

Глава 2.Обобщение имеющихся знаний о квадратных уравнениях и способах их решения

2.1. Определение квадратного уравнения

Определение: Квадратным уравнением называется уравнение вида

аx 2 + bx + c = 0, где х – переменная, а, b и с– некоторые числа, причем, а ≠ 0.

Числа а, b и с — коэффициенты квадратного уравнения. Число а называют первым коэффициентом, число b– вторым коэффициентом и число c – свободным членом.

● Пример. 8x 2 – 7x + 3 = 0

В каждом из уравнений вида ax 2 + bx + c = 0, где а ≠ 0, наибольшая степень переменной x – квадрат. Отсюда и название: квадратное уравнение.

Квадратное уравнение, в котором коэффициент при х 2 равен 1, называют приведенным квадратным уравнением.

● Пример. х 2 – 11х+30=0, х 2 – 8х= 0.

2.2. Решение квадратных уравнений с помощью выделения квадрата двучлена

Рассмотрим на примере решение квадратного уравнения, в котором оба коэффициента при неизвестных и свободный член отличны от нуля. Такой способ решения квадратного уравнения называют выделением квадрата двучлена.

Пример. Рассмотрим уравнение 7х 2 – 6х – 1= 0.

Разделив обе части этого уравнения на 7, получим равносильное ему приведенное квадратное уравнение

Выделим из трехчлена х 2 – x- –квадрат двучлена. Для этого разность

х 2 – х представим в виде х 2 – 2· х, прибавим к ней выражение и вычтем его. Получим

Отсюда х 2 – 2· х + = + ,

Следовательно, х — = – или х — = , ,

Уравнение имеет два корня: – и 1.

2.3. Решение квадратных уравнений по формуле

Решение квадратных уравнений выделением квадрата двучлена часто приводит к громоздким преобразованиям. Поэтому поступают иначе. Решают уравнение в общем виде и в результате получают формулу корней. Затем эту формулу применяют при решении любого квадратного уравнения. Решим квадратное уравнение

Разделив его обе части на а, получим равносильное ему приведенное квадратное уравнение

Выделим из трехчлена х 2 + х + квадрат двучлена. Для этого сумму

х 2 + х представим в виде х 2 +2х∙ ,прибавим к ней выражение

и вычтем его. Получим

Уравнение = равносильно уравнению ax 2 + bx + c = 0.

Число его корней зависит от знака дроби . Так как а ≠ 0, то 4a–положительное число, поэтому знак этой дроби определяется знаком его числителя, т. е. выражения b 2 – 4ас. Это выражение называют дискриминантом квадратного уравнения ax 2 + bx + c = 0. Его обозначают буквой D, т.е.

D = b – 4ас. Дискриминант квадратного уравнения ax 2 + bx + c = 0

– выражение b 2 – 4ас= D – по знаку которого судят о наличии у этого уравнения действительных корней.

Различные возможные случаи в зависимости от значения D.

1.Если D>0, то уравнение имеет два корня:

Пример. Рассмотрим уравнение 2x 2 –3x + 1= 0.

D= b – 4ас =(–3) – 4ас= 9–8= 1; 2 корня.

2.Если D= 0, то уравнение имеет один корень:

Пример. Рассмотрим уравнение 9х 2 +6х+1= 0.

D= b – 4ас=6 – 4ас=36–36= 0; 1 корень.

3. Если D 0. тогда это уравнение имеет два корня:

Найдем сумму и произведение корней:

Пример. Рассмотрим уравнение х 2 – 3х + 2 = 0.

D =1, уравнение имеет два корня. х₁ = 2 и х₂ = 1, p= –3; q= 2.

По теореме Виета x₁ + x ₂ =-p , значит 2 + 1= 3;

Следовательно, х ₁ = 2 и х₂ = 1 являются корнями уравнения х 2 – 3х + 2 = 0.

При D = 0 корни уравнения можно вычислить по формуле

Квадратное уравнение ax 2 + bx + c = 0 имеет корни х₁ и х ₂ равносильное ему приведенное квадратное уравнение имеет вид

Справедливо утверждение, обратное теореме Виета:

Теорема: Если числа m и n таковы, что их сумма равна –p, а произведение

равно q, то эти числа являются корнями уравнения х 2 + px + q = 0.

Пример. Рассмотрим уравнение х 2 +3х – 40=0.

По формуле корней квадратного уравнения получаем

Покажем, что корни уравнения найдены правильно. В уравнении

х 2 +3х – 40=0 коэффициент р равен 3, а свободный член q равен –40. Сумма найденных чисел –8 и 5 равна –3, а их произведение равно –40. Значит, по теореме, обратной теореме Виета, эти числа являются корнями уравнения

Итак, квадратные уравнения — это фундамент, на котором покоится величественное здание алгебры. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала некоторые из них, которые сама очень активно применяю.

Глава 3. Рациональные способы решения квадратного уравнения.

3.1.Свойства коэффициентов квадратного уравнения.

Пример. Рассмотрим уравнение х 2 +4х – 5= 0.

Значит, корнями этого уравнения являются 1 и –5. Проверим это с помощью нахождения дискриминанта:

D= b – 4ас= 4 – 4∙1∙(–5)= 36.

Отсюда следует, что если а+b+c= 0 , то х ₁ =1 , х ₂ =

Пример. Рассмотрим уравнение 2х 2 +8х +6 = 0.

2) Если b= а+c, то х₁ =-1, х ₂ = — . 8= 2+6

Значит корнями этого уравнения являются –1 и –3. Проверим это с помощью нахождения дискриминанта:

D= b – 4ас=8 – 4∙2∙6= 16.

Отсюда следует, что если b= а+c , то х₁ = -1 , х ₂ =

Пример 345х 2 – 137х – 208 = 0.

Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то

Пример 132х2 – 247х + 115 = 0.

Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то

3). Если второй коэффициент b = 2k – четное число, то формулу корней

Пример. Решим уравнение 3х 2 — 14х + 16 = 0.

Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;

D = k 2 – ac = (- 7) 2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;

3.2. Способ «переброски».

При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Если а±b+c≠0, то используется прием переброски:

2х 2 – 11х+5=0 х 2 – 11х+10= 0

х = 10; х =1. Корни уравнения необходимо поделить на 2.

4х 2 -37 х +9 =0 Ответ: ¼, 9

3.3.Закономерность коэффициентов

1) Если в уравнении ax 2 + bx + c = 0 коэффициент b равен (а 2 +1), а коэффициент с численно равен коэффициенту а, то его корни равны

ах 2 + (а 2 +1)∙ х+ а= 0

Пример. Рассмотрим уравнение 6х 2 +37х +6 = 0.

2) Если в уравнении ax 2 – bx + c = 0 коэффициент b равен (а 2 +1),а коэффициент с численно равен коэффициенту а, то его корни равны

ax 2 – (а 2 +1)∙ х+ а= 0

Пример. Рассмотрим уравнение 15х 2 –226х +15 = 0.

3) Если в уравнении ax 2 + bx – c = 0 коэффициент b равен (а 2 –1), а коэффициент с численно равен коэффициенту а, то его корни равны

ax 2 + (а 2 –1)∙ х– а= 0

Пример. Рассмотрим уравнение 17х 2 +288х – 17 = 0.

4) Если в уравнении ax 2 – bx – c = 0 коэффициент b равен (а 2 –1), а коэффициент с численно равен коэффициенту а, то его корни равны

ax 2 + (а 2 –1)∙ х– а= 0

Пример. Рассмотрим уравнение 10х 2 –99х – 10 = 0.

3.4.Графическое решение квадратного уравнения.

Если в уравнении

перенести второй и третий члены в правую часть, то получим

Построим графики зависимости у = х 2 и у = — px — q.

График первой зависимости — парабола, проходящая через начало координат. График второй зависимости —

прямая (рис.1). Возможны следующие случаи:

— прямая и парабола могут пересекаться в двух точках,

абсциссы точек пересечения являются корнями квад- ратного уравнения;

— прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;

— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.

1) Решим графически уравнение х 2 — 3х — 4 = 0 (рис. 2).

Решение. Запишем уравнение в виде х 2 = 3х + 4.

Построим параболу у = х 2 и прямую у = 3х + 4. Прямую

у = 3х + 4 можно построить по двум точкам М (0; 4) и

N (3; 13). Прямая и парабола пересекаются в двух точках

А и В с абсциссами х1 = — 1 и х 2 = 4. Ответ: х1 = — 1;

2) Решим графически уравнение (рис. 3) х 2 — 2х + 1 = 0.

Решение. Запишем уравнение в виде х 2 = 2х — 1.

Построим параболу у = х 2 и прямую у = 2х — 1.

Прямую у = 2х — 1 построим по двум точкам М (0; — 1)

и N(1/2; 0). Прямая и парабола пересекаются в точке А с

абсциссой х = 1. Ответ: х = 1.

3) Решим графически уравнение х 2 — 2х + 5 = 0 (рис. 4).

Решение. Запишем уравнение в виде х 2 = 5х — 5. Построим параболу у = х 2 и прямую у = 2х — 5. Прямую у = 2х — 5 построим по двум точкам М(0; — 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.

Ответ. Уравнение х 2 — 2х + 5 = 0 корней не имеет.

Итак, квадратным уравнением называется уравнение вида ax 2 + bx + c = 0. Квадратные уравнения бывают полными, неполными и приведенными. Способы решений полных уравнений различны: выделение квадрата двучлена, по формуле, по теореме Виета, способ переброски, способы, основанные на свойствах и закономерностях коэффициентов квадратного уравнения. В данной работе я изложила и показала на примерах все эти способы. Проанализировав дополнительный материал, я пришла к выводу, что с помощью рациональных способов решения квадратных уравнений , решать уравнения стало намного намного проще и быстрее.

Предложенные методы решения квадратных уравнений просты в применении, и они, безусловно, должно заинтересовать увлекающихся математикой учеников. Моя работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.

Заключение.

Таким образом, я считаю, что тема данного исследования полностью раскрыта. При работе над темой я узнала много нового из истории квадратных уравнений, а также научилась их решать более удобным способом. Полученные знания пригодятся мне в будущем.

В процессе работы мною создана система нестандартных приемов решения квадратных уравнений и разработан банк заданий, на основе которого мною проведена успешная апробация этих приемов. Хочется отметить и то, что излагаемая тема в этой работе еще полностью не изучена, она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Данный материал можно рекомендовать для внеклассных занятий по математике. Материалом могут воспользоваться те, кто любит математику и хочет знать о математике больше.

1.Алгебра 8 класс: учебник для общеобразовательных учреждений. Авторы: Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова. Издательство «Просвещение», Москва 2009 г.

2.Брадис В.М. Четырехзначные математические таблицы: для сред.шк.-57-е изд. – М.: Просвещение, 1990.

3. Штейнгауз В.Г. Математический калейдоскоп. – М.: Бюро «Квантум», 2005.

Решение уравнения методами группировки и замены переменной

Страницы работы

Содержание работы

Лабораторная работа №1

Цель работы: Решить уравнения методами:

б) замены переменной.

Теоретическая часть работы

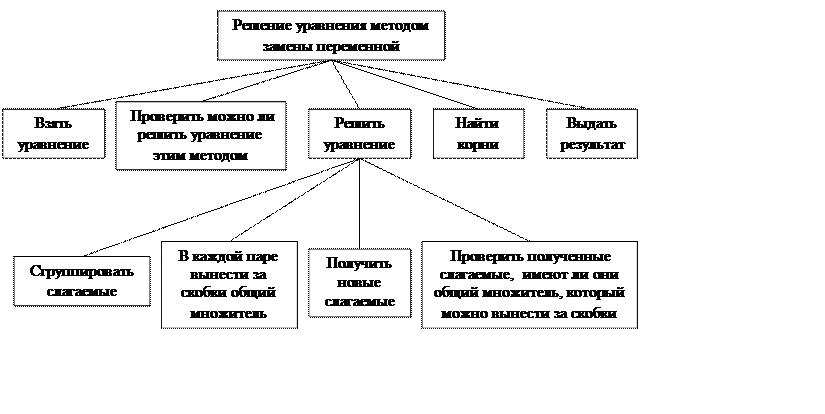
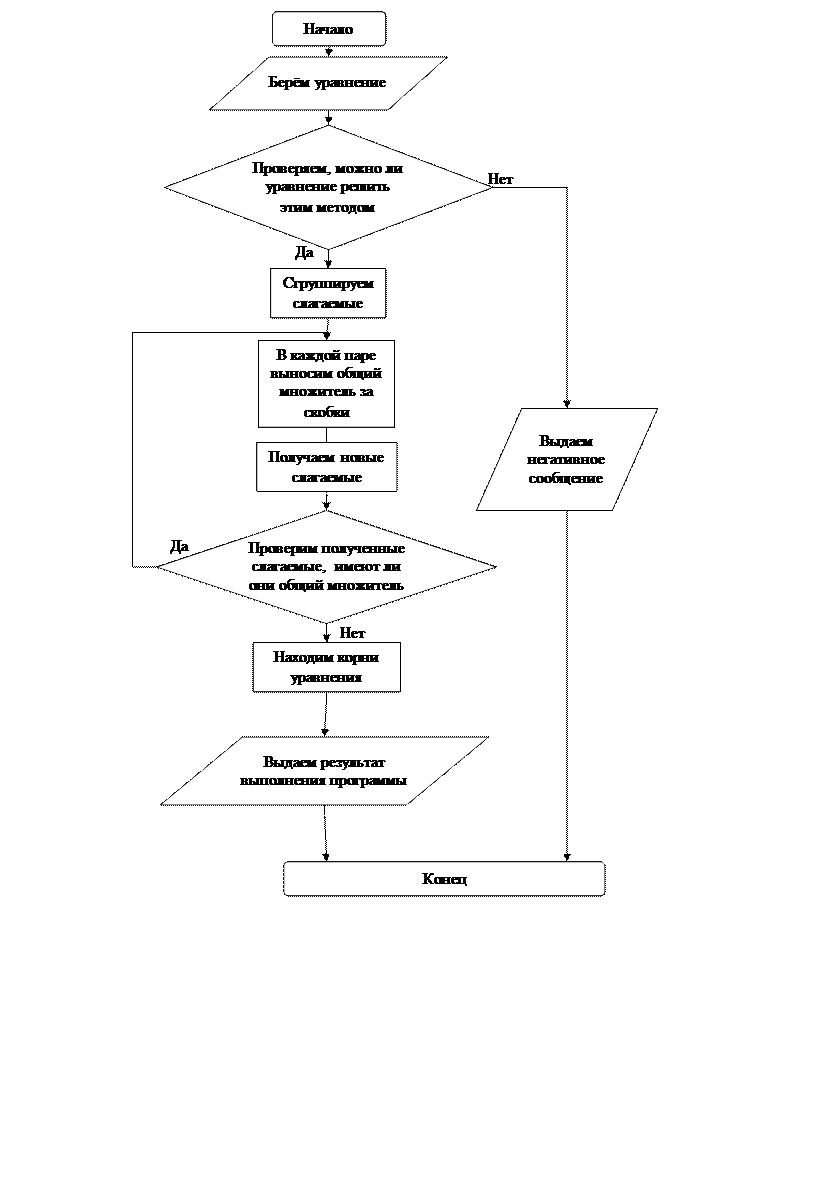
Способ группировки разложение на множители

Для того, чтобы разложить многочлен 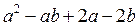на множители:

1 – Объединим слагаемые попарно в группы (говорят «сгруппируем слагаемые»): два в одну группу, и два — в другую .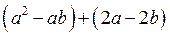

2 – В каждой паре вынесем за скобки общий множитель.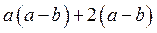

3 – Заметим, что оба полученных слагаемых также имеют общий множитель, который можно вынести за скобки .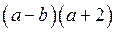

Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.

Рассмотрим решение уравнения способом разложения на множители на конкретном примере:

Применив способ группировки, получим:

Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:

Метод введения новой переменной

Пример.

.

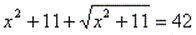
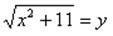
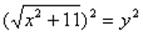
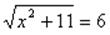
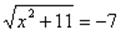
Введем новую переменную , учитывая, что , получаем квадратное уравнение у 2 +у – 42=0 , корни которого -7 и 6. Возвращаясь к переменной х, получаем уравнения и , последнее не имеет корней, т.к. арифметический квадратный корень – неотрицательное число, а первое уравнение можно решить, используя определение арифметического квадратного корня 6 2 = х 2 +11 , решение которого х=5 и х=-5.

Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.

Структурная схема программы: а) способ группировки разложение на множители

Блок-схема программы: а) способ группировки разложение на множители

Структурная схема программы: б) замены переменной

Блок-схема программы: б) замены переменной

«Нестандартные приемы решений квадратных уравнений»

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

Урок-конференция по математике для 8 класса

«Нестандартные приемы решений квадратных уравнений».

Учитель математики высшей категории

БОУ «Лицей № 102» г. Железногорск, Красноярский край

Скакунова Людмила Александровна

Материалы урока — конференции «Нестандартные приемы решений квадратных уравнений» соответствуют программным требованиям. В процессе подготовки и проведения этого урока реализуются основные виды УУД:

ориентация в системе знаний по заявленной теме;

постановка учебной задачи, анализ, синтез;

умение работать с информацией;

преобразовывать информацию из одной формы в другую: составлять ответы на вопросы; доказательства своих суждений;

умение формулировать проблему и находить способы её решения.

умение определять и формулировать цель;

планировать своё действие в соответствии с поставленной задачей;

вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок.

умение слушать и понимать речь других;

оформлять свои мысли в устной форме;

договариваться с одноклассниками совместно с учителем о правилах поведения и общения и следовать им.

Класс разбивается на группы (по числу докладов). Каждая группа работает над одной из предложенных тем. На уроке осуществляется представление и обсуждение каждого проекта.

Урок-конференция по теме

«Нестандартные приемы решений квадратных уравнений»

Л. А. Скакунова (Железногорск)

Подготовка к конференции

Класс (из 25 человек) разбивается на 5 групп (по числу докладов). Каждая группа работает над одной из предложенных тем по рекомендованной литерату­ре. Через две недели каждая группа в индивидуаль­ной беседе с учителем предлагает варианты изложе­ния темы, определяет докладчика (ученика, лучше других разобравшегося в материале) и его внутренне­го оппонента. Еще через неделю готовый доклад за­слушивается внутри группы, все ее члены знакомятся с содержанием и оформлением доклада (к выступ­лению докладчик готовит компьютерную презен­тацию).

Оборудование и материалы к уроку

Приборы и инструменты для выполнения чертежей и рисунков, компьютер, видеопроектор.

Стенды с материалами по теме конференции.

• Памятки для учащихся с алгоритмами различ­ных способов решения квадратных уравнений; вопросник для оппонентов; оценочный лист.

Основные этапы урока

Этап I . Организационный момент.

Этап II . Вступительное слово учителя.

Приветствие присутствующих, представление участников, сообщение о плане проведения конфе­ренции и порядке выступлений.

Этап III . Сообщения учащихся, выступления оп­понентов. Оценивание выступлений докладчиков.

Укажем перечень тем сообщений.

• Общие методы решения квадратных уравнений.

1. Метод разложения на множители.

2. Методом введения новой переменной.

• Специальные методы решения квадратных уравнений.

1. Использование свойства коэффициентов квад­ратного уравнения.

2. Метод «переброски» старшего коэффициента.

• Графический способ решения квадратных урав­нений.

• Геометрический способ решения квадратных уравнений.

• Способы решения квадратных уравнений в древности

После каждого сообщения заслушивается мнение оппонента. Приведем примерный план выступления оппонента (оценки доклада).

так, что вызывает интерес к теме; от простого к сложному; четко и ясно (или непоследовательно, неуверенно) и т.д.

В выступлении привлекались.

(Указываются средства привлечения внимания учащихся к излагаемому материалу.)

образная; математически грамотная; логически выдержан­ная и т.д.

интересное; новое для меня; может пригодиться в даль­нейшем; вызывает желание продолжить изучение вопроса, по­читать литературу по этой теме и т.д.

У меня следующий вопрос к выступающему. (Формулируется вопрос.)

Мои пожелания выступающему. (Высказываются пожелания.)

Далее каждый ученик класса заполняет полученный в начале урока оценочный лист и сдает его экспертной группе (в составе трех учеников старших классов).

В выступлении докладчика оцениваются (в баллах): знание содержания темы, решение примеров, а также презентация доклада.

0 – 4 балла: тема не раскрыта, допущены фактические и вычислительные ошибки, представление доклада не вызвало интереса к затронутому в нем вопросу;

5 – 7 баллов: тема раскрыта частично, встречались недочеты в решениях примеров, представление докладов в целом понравилось;

8 – 10 баллов: тема раскрыта полностью, не было допущено фактических и вычислительных ошибок, представление доклада вызвало интерес к рассматриваемому вопросу.

Экспертная группа обрабатывает результаты – суммирует выставленные учениками баллы и находит их среднее арифметическое. Кроме того, каждый член экспертной группы заполняет оценочный лист на оппонента (с последующей обработкой результатов – нахождением среднего арифметического баллов)

0 – 4 балла: представлен краткий комментарий, вопросы не задавались;

5 – 7 баллов: представлен подробный комментарий, вопросы не задавались;

8 – 10 баллов: представлен подробный комментарий, задавались вопросы по существу.

Все результаты заносятся в таблицу (используется компьютер).

Этап IV . Домашнее задание.

Задание состоит из подборки уравнений, предло­женных на уроке учениками, делавшими сообщения.

Этап V . Заключительное слово учителя.

После всех выступлений учитель дает оценку предварительной работе учащихся по подготовке к конференции (работе с дополнительной литературой по математике, подготовке презентаций и т.д.), а также прозвучавшим выступлениям; привлекает внимание к материалам стенда; сообщает о возмож­ности продолжить начатую работу.

Этап VI . Подведение итогов урока, выставление оценок докладчикам и лучшим оппонентам.

Тема 1. Общие методы решения квадратных уравнений

При решении квадратных уравнений часто при­меняется метод разложения на множители (с по­мощью вынесения за скобки общего множителя, фор­мул сокращенного умножения или способа группи­ровки).

Пример 1. Решите уравнение

Решение. Воспользуемся способом группировки.

3х² + 3х – х – 1 = 0,

3х(х + 1) – (х + 1) = 0,

х + 1 = 0 или 3х – 1 = 0,

х = -1 х = .

Ответ: -1; .

При решении более сложных квадратных уравнений нередко приходится использовать метод введения новой переменной. Удачный выбор новой переменной делает структуру уравнения более прозрачной и позволяет свести решение к более простому случаю.

Пример 2. Решите уравнение

.

Решение. Пусть t = 5х + 3. Произведем замену переменной:

Убеждаемся, что D > 0. По теореме, обратной теореме Виета, подбираем корни: t ₁ = 1, t ₂ = 2.

Произведем обратную замену и вернемся к переменной х.

Если t = 1, то Если t = 2, то

Замечание. При решении квадратного уравнения не следует торопиться выполнять преобразования. Сначала надо посмотреть, нельзя ли записать уравнение проще, введя новую переменную.

Задание на дом. Решите уравнения, используя метод разложения на множители или введение новой переменной.

х 2 + 16х + 15 = 0; (3х + 2)² = 4 + 12х.

Тема 2. Специальные методы решения квадратных уравнений

Рассмотрим решение квадратных уравнений, коэффициенты которых обладают определенными свойствами. Установим связь между суммой коэффициентов уравнения и его конями.

1) х² +4х – 5 = 0, 2) х² + 6х + 5 = 0,

a = 1, b = 4, c = — 5, a = 1, b = 6, c = 5,

a + b + c = 0, a + c = b,

3) 2х² — 5х + 3 = 0, 4) 3х² + 2х – 1 = 0,

a = 2, b = — 5 , c = 3 , a = 3 , b = 2 , c = — 1 ,

a + b + c = 0, a + c = b,

х₁ = 1, х₂ = х₁ = — 1, х₂ =

Вывод: при решении уравнения ах² + b х + c = 0 (a ≠ 0) можно пользоваться следующими утверждениями:

Если a + b + c = 0, то х₁ = 1, х₂ =

1) Разделим обе части уравнения на а ≠ 0 и получим:

х² + х + = 0.

2) По теореме Виета х₁ + х₂ = —,

х₁ · х₂ = ;

х₁ + х₂ = — = 1 + , х₁ = 1,

х₁ ∙ х₂ = 1 ∙ ; х₂ = .

Если a + с = b , то х₁ = — 1, х₂ = —

1) По теореме Виета х₁ + х₂ = —,

х₁ · х₂ = ;

2) Так как а +с = b , то

х₁ + х₂ = — = -1 –, х₁ = — 1,

х₁ · х₂ = -1 ∙ ( — ); х₂ = — .

Задание (устно). Найдите корни уравнения:

а) 3х² — 8х + 5 = 0; в) 5х² — 9х – 14 = 0;

б) 2х² + 3х + 1 = 0; г) — х² — 4х – 3 = 0.

Другой метод решения квадратных уравнений – метод «переброски» старшего коэффициента. Умножим обе части уравнения на а ≠ 0:

Пусть ах = у, тогда .

Корни у₁ и у₂ уравнения найдем по теореме, обратной теореме Виета. Так как

Пример. Решите уравнение

По теореме, обратной теореме Виета, имеем:

Замечание: Данный метод хорош для квадратных уравнений с “удобными” коэффициентами. В некоторых случаях позволяет решить квадратное уравнение устно.

Задание на дом. Решите уравнения, используя с пециальные методы решения квадратных уравнений .

1907х 2 + 101х — 2008 = 0; х 2 + 12х + 20 = 0.

Тема 3. Графический способ решения квадратных уравнений

Графический способ решения квадратного уравнения состоит в построении на одной координатной плоскости графиков двух функций и нахождении абсцисс их точек пересечения (если такие точки есть).

В случае квадратного уравнения строятся графики квадратичной и линейной функций: парабола и прямая. Возможны следующие случаи (рис. 1):

1) прямая и парабола касаются (имеют единственную общую точку), абсцисса точки касания – корень уравнения;

2) прямая и парабола пересекаются в двух точках, абсциссы этих точек являются корнями уравнения;

3) прямая и парабола не имеют общих точек, в этом случае уравнение не имеет корней.

Пример. Решим графически следующее уравнение

x 2 + 1,5х — 2,5 = 0.

Перепишем уравнение в виде x 2 = — 1,5х + 2,5.

Рассмотрим функции у = x 2 и у = — 1,5х + 2,5.
Построим в одной координатной плоскости графики этих функций (рис. 2), и найдем точки пересечения : х₁ = — 2,5, х₂ = 1. Эти числа являются корнями исходного уравнения.

Задание на дом. Решите уравнения, используя графический способ.

— 2х ² + 8 = 0; х² — 2х = 0.

Тема 4. Геометрический способ решения квадратного уравнения

Рассмотрим решение квадратных уравнений с помощью циркуля и линейки.

Дано уравнение ах² + bx + c = 0

1) Построим точки Q (-; )(центр окружности) и А (0;1).

2) Проведём окружность с радиусом QA .

3) Абсциссы точек пересечения окружности с ОХ являются корнями квадратного уравнения.

Условия количества корней (рис. 3):

1) Если R >, то окружность пересекает ОХ в двух точках M (х₁; 0) и N ( x ₂; 0), где х и х₂ – корни уравнения.

2) Если R = , то окружность касается ОХ в точке M (х₁;0), где х₁– корень уравнения.

нет.

Примеры. Решить квадратные уравнения с помощью циркуля и линейки (рис. 4).

Задание на дом. Решите уравнения с помощью циркуля и линейки.

х ² — 4 х + 3 = 0; х ² + 2х = 0;

Тема 5. Как решали квадратные уравнения в древности

Впервые квадратное уравнение сумели решить математики Древнего Египта. В одном из математических папирусов содержится задача:

«Найти стороны поля, имеющего форму прямоугольника, если его площадь 12, а длины равны ширине».

Пусть х – длина поля. Тогда х – его ширина, S = — площадь. Получилось квадратное уравнение = 12. В папирусе дано правило для его решения: «Раздели 12 на ».

Итак, х² = 16. «Длина поля равна 4» — указано в папирусе.

Рассмотрим способ решения квадратного уравнения среднеазиатского ученого ал – Хорезми из трактата «Хисаб ал – джебр валь – мукабала»:

Решить квадратное уравнение х² + 10х = 39.

Решение самого ал – Хорезми:

Строим квадрат х² (рис. 5). На сторонах его строим четыре равных прямоугольника с общей площадью 10х. Площадь каждого будет , а измерения х и . Теперь фигуру, имеющую форму креста, дополняем до квадрата четырьмя равными квадратами в углах фигуры. Площадь каждого такого квадрата будет равняться . Площадь всех четырех квадратов составит · 4 = 25. Таким образом, площадь всего составленного квадрата будет: Рис. 5

Задание на дом. Составив квадратное уравнение, решите древнеиндийскую задачу о стае обезьян.

Обезьянок резвых стая

Всласть поевши, развлекалась.

Их в квадрате часть восьмая

На поляне забавлялась.

А двенадцать по лианам стала

Сколько ж было обезьянок,

Ты скажи мне, в этой стае?

Пресман А.А. Решение Квадратного уравнения с помощью циркуля и линейки. – М., Квант, № 4/72.

Энциклопедический словарь юного математика/ Сост. А. П. Савин – 3-е изд., испр. И доп. – М.: Педагогика – Пресс, 1997

Энциклопедия для детей Т. 11 Математика / Глав. Ред. М. Д. Аксенова. – М.: Аванта +, 2000.

Краткое описание документа:

Материалы урока — конференции «Нестандартные приемы решений квадратных уравнений» соответствуют программным требованиям. В процессе подготовки и проведения этого урока реализуются основные виды УУД: Познавательные:- ориентация в системе знаний по заявленной теме;- постановка учебной задачи, анализ, синтез; — умение работать с информацией; — преобразовывать информацию из одной формы в другую: составлять ответы на вопросы; доказательства своих суждений; — умение формулировать проблему и находить способы её решения. Регулятивные:- умение определять и формулировать цель;- планировать своё действие в соответствии с поставленной задачей;- вносить необходимые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок. Коммуникативные:- умение слушать и понимать речь других; — оформлять свои мысли в устной форме;- договариваться с одноклассниками совместно с учителем о правилах поведения и общения и следовать им. Класс разбивается на группы (по числу докладов). Каждая группа работает над одной из предложенных тем. На уроке осуществляется представление и обсуждение каждого проекта.