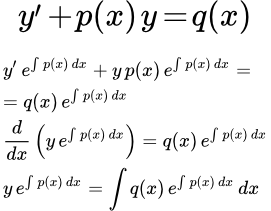Как решать неоднородные уравнения первого порядка

Решение линейных дифференциальных уравнений первого порядка

Определения и методы решений

Линейное дифференциальное уравнение первого порядка – это уравнение вида
,
где p и q – функции переменной x .

Линейное однородное дифференциальное уравнение первого порядка – это уравнение вида
.

Линейное неоднородное дифференциальное уравнение первого порядка – это уравнение вида
.

Член q ( x ) называется неоднородной частью уравнения.

Рассмотрим линейное неоднородное дифференциальное уравнение первого порядка:
(1) .
Существует три способа решения этого уравнения:

Решение линейного дифференциального уравнения с помощью интегрирующего множителя

Рассмотрим метод решения линейного дифференциального уравнения первого порядка с помощью интегрирующего множителя.
Умножим обе части исходного уравнения (1) на интегрирующий множитель
:
(2)
Далее замечаем, что производная от интеграла равна подынтегральной функции:

По правилу дифференцирования сложной функции:

По правилу дифференцирования произведения:

Подставляем в (2):

Интегрируем:

Умножаем на . Получаем общее решение линейного дифференциального уравнения первого порядка:

Пример решения линейного дифференциального уравнения первого порядка

Разделим обе части исходного уравнения на x :
(i) .
Тогда
;
.
Интегрирующий множитель:

Знак модуля можно опустить, поскольку интегрирующий множитель можно умножать на любую постоянную (в том числе на ± 1 ).
Умножим (i) на x 3 :
.
Выделяем производную.
;
.
Интегрируем, применяя таблицу интегралов:
.
Делим на x 3 :
.

Использованная литература:
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 22-07-2012 Изменено: 25-02-2015

Линейные неоднородные дифференциальные уравнения первого порядка

В данной теме поговорим о способах решения линейных неоднородных дифференциальных уравнений вида y ‘ = P ( x ) · y = Q ( x ) . Начнем с метода вариации произвольной постоянной и покажем способ применения этого метода для решения задачи Коши. Продолжим рассмотрением метода, который предполагает представление произвольной постоянной у как произведения двух функций u ( x ) и v ( x ) . В разделе мы приводим большое количество задач по теме с детальным разбором решения.

На тот случай, если применяемые при разборе темы термины и понятия окажутся незнакомыми для вас, мы рекомендуем заглядывать в раздел «Основные термины и определения теории дифференциальных уравнений».

Метод вариации произвольной постоянной для решения ЛНДУ первого порядка

Для краткости будет обозначать линейное неоднородное дифференциальное уравнение аббревиатурой ЛНДУ, а линейное однородное дифференциальное уравнение (ЛОДУ).

ЛНДУ вида y ‘ = P ( x ) · y = Q ( x ) соответствует ЛОДУ вида y ‘ = P ( x ) · y = 0 , при Q ( x ) = 0 . Если посмотреть на дифференциальное уравнение y ‘ = P ( x ) · y = 0 , становится понятно, что мы имеем дело с уравнением с разделяющимися переменными. Мы можем его проинтегрировать: y ‘ = P ( x ) · y = 0 ⇔ d y y = — P ( x ) d x , y ≠ 0 ∫ d y y = — ∫ P ( x ) d x ⇔ ln y + C 1 = — ∫ P ( x ) d x ⇔ ln y = ln C — ∫ P ( x ) d x , ln C = — C 1 , C ≠ 0 ⇔ e ln y = e ln C — ∫ P ( x ) d x ⇔ y = C · e — ∫ P ( x ) d x

Мы можем утверждать, что значение переменной y = 0 тоже является решением, так как при этом значении переменной уравнение y ‘ = P ( x ) · y = 0 обращается в тождество. Этому случаю соответствует решение y = C · e — ∫ P ( x ) d x при значении C = 0 .

Получается, что y = C · e — ∫ P ( x ) d x — общее решение ЛОДУ, где С – произвольная постоянная.

y = C · e — ∫ P ( x ) d x — это решение ЛОДУ y ‘ = P ( x ) · y = 0 .

Для того, чтобы найти общее решение неоднородного уравнения y ‘ = P ( x ) · y = Q ( x ) , будем считать С не константой, а функцией аргумента х . Фактически, мы примем y = C ( x ) · e — ∫ P ( x ) d x общим решением ЛНДУ.

Подставим y = C ( x ) · e — ∫ P ( x ) d x в дифференциальное уравнение y ‘ = P ( x ) · y = Q ( x ) . Оно при этом обращается в тождество:

y ‘ = P ( x ) · y = Q ( x ) C x · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Теперь обратимся к правилу дифференцирования произведения. Получаем:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x )

Производная сложной функции e — ∫ P ( x ) d x ‘ равна e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ .

Теперь вспомним свойства неопределенного интеграла. Получаем:

e — ∫ P ( x ) d x · — ∫ P ( x ) d x ‘ = — e — ∫ P ( x ) d x · P ( x )

Теперь выполним переход:

C ‘ ( x ) · e — ∫ P ( x ) d x + C ( x ) · e — ∫ P ( x ) d x ‘ + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x — P ( x ) · C ( x ) · e — ∫ P ( x ) d x + P ( x ) · C ( x ) · e — ∫ P ( x ) d x = Q ( x ) C ‘ ( x ) · e — ∫ P ( x ) d x = Q ( x )

Так мы пришли к простейшему дифференциальному уравнению первого порядка. В ходе решения этого уравнения мы определим функцию C ( x ) . Это позволит нам записать решение исходного ЛНДУ первого порядка следующим образом:

y = C ( x ) · e — ∫ P ( x ) d x

Подведем итог

Метод вариации произвольной постоянной при решении ЛНДУ предполагает проведение трех этапов:

• нахождение общего решения соответствующего ЛОДУ y ‘ + P ( x ) · y = 0 в виде y = C · e — ∫ P ( x ) d x ;
• варьирование произвольной постоянной С , что заключается в замене ее функцией С ( x ) ;
• подстановка функции y = C ( x ) · e — ∫ P ( x ) d x в исходное дифференциальное уравнение, откуда мы можем вычислить C ( x ) и записать ответ.

Теперь применим этот алгоритм к решению задачи.

Найдите решение задачи Коши y ‘ — 2 x y 1 + x 2 = 1 + x 2 , y ( 1 ) = 3 .

Нам нужно отыскать частное решение ЛНДУ y ‘ — 2 x y 1 + x 2 = 1 + x 2 при начальном условии y ( 1 ) = 3 .

В нашем примере P ( x ) = — 2 x 1 + x 2 и Q ( x ) = x 2 + 1 . Начнем с того, что найдем общее решение ЛОДУ. После этого применим метод вариации произвольной постоянной и определим общее решение ЛНДУ. Это позволит нам найти искомое частное решение.

Общим решением соответствующего ЛОДУ y ‘ — 2 x y 1 + x 2 = 0 будет семейство функций y = C · ( x 2 + 1 ) , где С – произвольная постоянная.

Варьируем произвольную постоянную y = C ( x ) · ( x 2 + 1 ) и подставляем эту функцию в исходное уравнение:
y ‘ — 2 x y 1 + x 2 = 1 + x 2 C x · ( x 2 + 1 ‘ — 2 x · C ( x ) · ( x 2 + 1 ) 1 + x 2 = 1 + x 2 C ‘ ( x ) · ( x 2 + 1 ) + C ( x ) · 2 x — 2 x · C ( x ) = 1 + x 2 C ‘ ( x ) = 1 ,

откуда C ( x ) = ∫ d x = x + C 1 , где C 1 – произвольная постоянная.

Это значит, что y = C ( x ) · ( x 2 + 1 ) = ( x + C 1 ) · ( x 2 + 1 ) — общее решение неоднородного уравнения.

Теперь приступим к отысканию частного решения, которое будет удовлетворять начальному условию y ( 1 ) = 3 .

Так как y = ( x + C 1 ) · ( x 2 + 1 ) , то y ( 1 ) = ( 1 + C 1 ) · ( 1 2 + 1 ) = 2 · ( 1 + C 1 ) . Обратившись к начальному условию, получаем уравнение 2 · ( 1 + C 1 ) = 3 , откуда C 1 = 1 2 . Следовательно, искомое решение задачи Коши имеет вид y = x + 1 2 · ( x 2 + 1 )

Теперь рассмотрим еще один метод решения линейных неоднородных дифференциальных уравнений y ‘ + P ( x ) · y = Q ( x ) .

Еще один метод решения ЛНДУ первого порядка

Мы можем представить неизвестную функцию как произведение y = u ⋅ v , где u и v – функции аргумента x .

Мы можем подставить эту функцию в ЛНДУ первого порядка. Имеем:

y ‘ + P ( x ) · y = Q ( x ) ( u · v ) ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · v ‘ + P ( x ) · u · v = Q ( x ) u ‘ · v + u · ( v ‘ + P ( x ) · v ) = Q ( x )

Если найти такое v , чтобы оно было ненулевым частным решением дифференциального уравнения v ‘ + P ( x ) · v = 0 , то u можно будет определить из уравнения с разделяющимися переменными u ‘ · v = Q ( x ) .

Рассмотрим этот алгоритм решения на предыдущем примере. Это позволит нам сосредоточиться на главном, не отвлекаясь на второстепенные детали.

Найдите общее решение линейного неоднородного дифференциального уравнения y ‘ — 2 x y 1 + x 2 = 1 + x 2 .

Пусть y = u ⋅ v , тогда
y ‘ — 2 x y x 2 + 1 = x 2 + 1 ⇔ ( u · v ) — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · u · v x 2 + 1 = x 2 + 1 u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1

Находим такое v , отличное от нуля, чтобы выражение в скобках обращалось в ноль. Иными словами, находим частное решение дифференциального уравнения v ‘ — 2 x · v x 2 + 1 = 0 .
v ‘ — 2 x · v x 2 + 1 = 0 ⇔ d v d x = 2 x · v x 2 + 1 ⇒ d v v = 2 x d x x 2 + 1 ⇔ d v v = d ( x 2 + 1 ) x 2 + 1 ∫ d v v = ∫ d ( x 2 + 1 ) x 2 + 1 ln v + C 1 = ln ( x 2 + 1 ) + C 2

Возьмем частное решение v = x 2 + 1 , соответствующее C 2 – С 1 = 0 .

Для этого частного решения имеем
u ‘ · v + u · v ‘ — 2 x · v x 2 + 1 = x 2 + 1 ⇔ u ‘ · ( x 2 + 1 ) + u · 0 = x 2 + 1 ⇔ u ‘ = 1 ⇔ u = x + C

Следовательно, общее решение исходного линейного неоднородного дифференциального уравнения есть y = u · v = ( x + C ) · ( x 2 + 1 )

Ответы в обоих случаях совпадают. Это значит, что оба метода решения, которые мы привели в статье, равнозначны. Выбирать, какой из них применить для решения задачи, вам.

Линейные дифференциальные уравнения 1-го порядка
и уравнение Бернулли

Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и её производной. Оно имеет вид

где и — заданные функции от , непрерывные в той области, в которой требуется проинтегрировать уравнение (1).

Если , то уравнение (1) называется линейным однородным . Оно является уравнением с разделяющимися переменными и имеет общее решение

Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной , который состоит в том, что решение уравнения (1) ищется в виде

Пример 1. Решить уравнение .

Решение. Применим метод вариации постоянной. Рассмотрим однородное уравнение , соответствующее данному неоднородному уравнению. Это уравнение с разделяющимися переменными. Его общее решение имеет вид .

Общее решение неоднородного уравнения ищем в виде , где — неизвестная функция от . Подставляя, получаем , откуда . Итак, общее решение неоднородного уравнения будет , где — постоянная интегрирования.

Замечание. Может оказаться, что дифференциальное уравнение линейно относительно как функция от . Нормальный вид такого уравнения

Пример 2. Решить уравнение .

Решение. Данное уравнение является линейным, если рассматривать как функцию от :

Применяем метод вариации произвольной постоянной. Сначала решаем соответствующее однородное уравнение

которое является уравнением с разделяющимися переменными. Его общее решение имеет вид .

Общее решение уравнения ищем в виде , где — неизвестная функция от . Подставляя, получаем

Отсюда, интегрируя по частям, будем иметь

Исходное уравнение может быть проинтегрировано также следующим образом. Полагаем

где и — неизвестные функции от , одна из которых, например , может быть выбрана произвольно.

Подставляя в , после преобразования получаем

Определяя из условия , найдем затем из функцию , а следовательно, и решение уравнения . В качестве можно взять любое частое решение уравнения .

Пример 3. Решить задачу Коши: .

Решение. Ищем общее решение уравнения в виде ; имеем . Подставляя выражение для и в исходное уравнение, будем иметь

Функцию находим из условия . Беря любое частное решение последнего уравнения, например , и подставляя его, получаем уравнение , из которого находим функцию . Следовательно, общее решение уравнения будет

Используя начальное условие , получаем для нахождения уравнение , откуда ; так что решением поставленной задачи Коши будет функция .

Пример 4. Известно, что между силой тока и электродвижущей силой в цепи, имеющей сопротивление и самоиндукцию , существует зависимость , где и — постоянные. Если считать функцией времени , то получим линейное неоднородное уравнение для силы тока :

Найти силу тока для случая, когда и .

Решение. Имеем . Общее решение этого уравнения имеем вид . Используя начальное условие (13), получаем из , так что искомое решение будет

Отсюда видно, что при сила тока стремится к постоянному значению .

Пример 5. Дано семейство интегральных кривых линейного неоднородного уравнения .

Показать, что касательные в соответственных точках к кривым , определяемым линейным уравнением, пересекаются в одной точке (рис. 13).

Решение. Рассмотрим касательную к какой-либо кривой в точке .Уравнение касательной в точке имеет вид

По определению, в соответственных точках является постоянным, а переменным. Беря любые две касательные к линиям в соответственных точках, для координат точки их пересечения, получаем

Отсюда видно, что все касательные к кривым в соответственных точках ( фиксировано) пересекаются в одной и той же точке

Исключая в системе аргумент , получаем уравнение геометрического места точек .

Пример 6. Найти решение уравнения , удовлетворяющее условию: ограничено при .

Решение. Общее решение данного уравнения . Любое решение уравнения, получаемое из общего решения при , будет неограниченно, так как при функция ограничена, а . Отсюда следует, что данное уравнение имеет единственное решение , ограниченное при , которое получается из общего решения при .

Уравнение Бернулли

Дифференциальное уравнение Бернулли имеет вид

С помощью замены переменной уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.

Пример 7. Решить уравнение Бернулли .

Решение. Делим обе части уравнения на :

Делаем замену переменной , откуда . После подстановки последнее уравнение обратится в линейное уравнение

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариации постоянной, как и линейное уравнение, и с помощью подстановки .

Пример 8. Решить уравнение Бернулли .

Решение. Применим метод вариации произвольной постоянной. Общее решение соответствующего однородного уравнения имеет вид . Общее решение уравнения ищем в виде , где — новая неизвестная функция. Подставляя в исходное уравнение, будем иметь

Для нахождения функции получим уравнение с разделяющимися переменными, из которого, разделяя переменные и интегрируя, найдем

Итак, общее решение исходного уравнения .

Некоторые нелинейные уравнения первого порядка с помощью удачно найденной замены переменных сводятся к линейным уравнениям или к уравнениям Бернулли.

Пример 9. Решить уравнение .

Решение. Запишем данное уравнение в виде .

Деля обе части уравнения на , получаем .

Замена приводит это уравнение к линейному , общее решение которого .

Заменяя его выражением через , получаем общий интеграл данного уравнения .

В некоторых уравнениях искомая функция может находиться под знаком интеграла. В этих случаях иногда удается путем дифференцирования свести данное уравнение к дифференциальному.

Пример 10. Решить уравнение 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAUQAAABNBAMAAAAsvACJAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAD3RSTlMAAUbAgWgQITGh8LHQkeBuUEPaAAAHI0lEQVRo3u1afWxTVRQ/97XvtbUbvG6OwJxrmcMpzHRjgBLULQRJEGTFMBMRWQMaiSBrMBJCjBtEQSdmi5sJEc0o4hAXQ8N3gnEDEwxfo3HxD8jIhMlfRnHdxjYm1HPfu+36um4QPCRN2E229vX1nv7u+fj9zr0twNh4AIcyxZfsEFfl/ZLsEF+DBckO8RBMpTZpca0ntTcD3CotQjYl/6KHGCK1F4OVa1xJDhGWA2lg6mEFOcSvFS9l4uTDZWKA1r6rMiVEmPTbEeqCPr/gV1qLG+8Dk7Ex1U7C4Uh6k9bOWmqE1s4CUnubXt5NDXHd3G9J7X35SC81xNI3ekhZbMDyCjXlNCnzKe1lhBhxpwNpxGFJv0Fez7Z+WnsVJ8ghZvpp7bnJKQdqaCmHdXioEbLyElp7F6rIvdhM2nODElbJvbifdmcudZM70XqTdtWPDsS69Cj//+5oLbM1MMINU3RWRnccRFlL9x33TIuxUmXSkkgSKOSiBJW0PSF+C846Fbmw3xp2mqAJtwj/tNl3yJOcuBU6QzEXC/ENT4CjXjgM035LvIGTCeXkIFp9KXKVLcTlzQj+RrTlgbQW/fK9AVBGYRE29fLVOFrsi4nzd/iHLqgWnurwQmecAbkldomy/mD+k4e2MlIklaHodF1skIPsu4BdE9nfC7auUXqG3bDMZ+SwGCUwt+j6mqLzGjsH1viOJduw/nSB18Eh2oQGMLcA0CrucuzOALAV+rW5D8YNU7TPoqhsu8AZNNxriFECDi0VvWrWLaBD5VC8cPgSQWQcohxZbOmVyHR9LMabbk90rukKVAaHEcvsiOFxhZCOBt6ZIc8Qxq/r7/70GKS5KlxgXtxTAhLvLJS2L0LmRT3z44RD5bNXPifKKxbiRNE8sGKt3NIWDM5V2lzwEcwBWFpc74NMj1aDNbW5DfURckdbevVIRZNFcSDELlCeyfrD7RLMrUVOmTUH3euugpXuAy6wcN9VLym/Ibmn87etz+Ejj7+xTgXlWNbpak+cF/k/USUsrOWJdVooz5bbBT+pewC2nMnxQjpmgvLzW/s9W4pzRJoikogtS52O0V3Imy97lcnfrOueFNYezZMHmduDLmI8IvzDlCZ46ATUaNNz5/Exlz8twmRxmRobXMMDzUTeWsP6zawT8KR9F2vir7NB7nPMKXsjdPhYZ6Tm0NYNYQssXy3RIBaAKYSF6KxdLSpE1z8Zk67DV4rPO3z6h9lCUBGE8hgB550vQ4gSZAb4bHnevMWI3BuFuEeUeVhPK5yeV1Er9fIFS9zDpkIEEGTPq5aeIUrILlgdORewtLuiEJmWvTrNCiWw+1mryhOtVfgj088wF5rjWJRDdAjfZowAMVXXPz4dyl3mfg7R3C8gNrjYgKEIK4e6ImURh1ih5SIWXaR+skXZZQaUAX4WqnA95BArC5HX2DfazQ8NgQbhW4eaONDp3UO02Kya/Px1k18PNCtWOS3GNPrl0a4IA839mVkIWX5YU3JGFdadvZHFICFiuaT1WgJauVSUsHOTNvYoLcZyaVPBFmxWs9QEuShMZepQWSuqchGMD3DvOgPpWC7Ijc8iq5Vlt9iqZM1JMbYsdTpYJHlnLbh3dMMLQlwEU1SUmPrA6cIYmKpAQm4cF7QNrpVCtrjWD3PBfeQ2LI2j7n8dWCYho7h0o9b/COUeOI4QS3BGJsb0ElT/c9QZfB3cjdrHz/pe2JLqJus5KYUAU2Rd+/ttQkDKhRLIP7RegfQSmNCEImxG6rT+NfPSAeXs4TiKRaVY255fFzRANIfDWMWyMOUWYby00wvVO69XcVWxncYZNZgfq45/vi+Yuq8WNmkLSWnP3xnUqTvqi2Vl/JxgM9ssrjsi4rIS81bmAuhVIYXPmqhafCB5EwjgZtgaL4AO9KItYBAXsCAiR16rLoDb8AVNADfAau2KaamNtjZoj58MqZalzCjRxbo/LE3wohcm7B0S1RGGbNg5ZRi2ksIPzUMdZUoXZxubiNg1g6XCEVsdI4swQbNSr8wPdsSXRPWjdHMnR7QW+YbpwlCn4Sz4oFZvxvhn/G4Q5eDdnpYImlUOnvVpZK+p66lRZmwfqSW3njKuWm+KZ/KHV/WW1rCPs3nvdudyW431h/L0nTcGI2277SI7pNj9mn7OKGugj93btuDhAfLNlZxgv/Z/tlt28nM7SO2htZfdTw7RFCI+c/KTQ3R2PWhnTlBKfubERZl0FHvJITbQHmOJfpDU5N+k5rZJ5JzzsYWUc6w3J1EXNAtn7CU9Wrz1tosa4r51tCe0y6+Rfym7/DniNav01UJPEWMjGYeS60t2iCmPT092iI+Jg22q8dShuipiiBdpfzulBKeOp+Zu4h/JKd6F5IFGiLTMOPN+QKT0otQSSqUWgzbaH2zK5w+VUXtxO/HPXrdayXk29fCspJeXjTA2kmX8B/XH3ORQKCpxAAAAAElFTkSuQmCC» style=»vertical-align: middle;» />.

Решение. Дифференцируя обе части этого уравнения по , получаем

Дифференцируя еще раз по , будем иметь линейное однородное уравнение относительно

Разделяя переменные и интегрируя, найдем . Это решение, как легко проверить, удовлетворяет исходному уравнению.