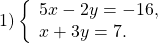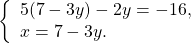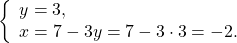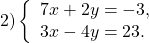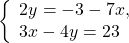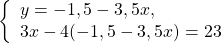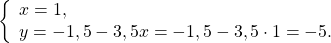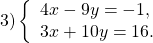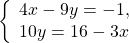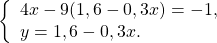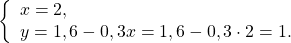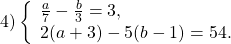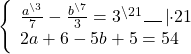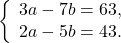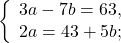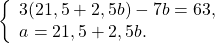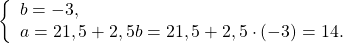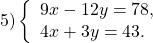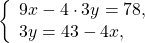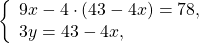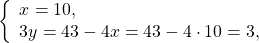Как решать способом подстановки систему уравнений примеры

Примеры решения систем линейных уравнений методом подстановки

Рассмотрим конкретные примеры решения систем линейных уравнений методом подстановки.

В данном случае удобно из второго уравнения системы выразить x через y и подставить полученное выражение вместо x в первое уравнение:

Первое уравнение — уравнение с одной переменной y. Решаем его:

Полученное значение y подставляем в выражение для x:

В данной системе проще из первого уравнения выразить y через x и подставить полученное выражение вместо y во второе уравнение:

Второе уравнение — уравнение с одной переменной x. Решим его:

В выражение для y вместо x подставляем x=1 и находим y:

Здесь удобнее из второго уравнения выразить y через x (поскольку делить на 10 проще, чем на 4, -9 или 3):

Решаем первое уравнение:

Подставляем x=2 и находим y:

Прежде чем применить метод подстановки, эту систему следует упростить. Обе части первого уравнения можно умножить на наименьший общий знаменатель, во втором уравнении раскрываем скобки и приводим подобные слагаемые:

Получили систему линейных уравнений с двумя переменными. Теперь применим подстановку. Удобно из второго уравнения выразить a через b:

Решаем первое уравнение системы:

3(21,5 + 2,5b) — 7b = 63

Осталось найти значение a:

Согласно правилам оформления, ответ записываем в круглых скобках через точку с запятой в алфавитном порядке.

Выражая одну переменную через другую, иногда удобнее оставлять её с некоторым коэффициентом.

В данном случае удобно выразить y через x из второго уравнения. При этом лучше не делить обе части уравнения на 3, а оставить коэффициент 3 рядом с y, поскольку в первом уравнении 12y кратно 3:

Из всех способов решения систем уравнений метод подстановки в алгебре используется чаще других. С помощью этого метода могут быть решены не только системы линейных уравнений, но и системы уравнений других видов.

Решение системы линейных уравнений методом подстановки

Алгоритм решения системы линейных уравнений методом подстановки

1. Из любого уравнения системы выразить одну переменную через другую.
2. Подставить во второе уравнение системы вместо переменной выражение, полученное на первом шаге.
3. Решить второе уравнение относительно выраженной переменной.
4. Подставить найденное значение переменной в выражение, полученное на первом шаге.
5. Найти значение второй переменой.
6. Записать ответ в виде упорядоченной пары найденных значений переменных.

Из второго уравнения выражаем y:

Подставляем выражение для y в первое уравнение:

Шаг 3 Решаем первое уравнение:

Подставляем значение x в выражение для y:

В последовательной записи:

$$ <\left\< \begin 3x+y = 5 \\ y-x = 1 \end \right.> \Rightarrow <\left\< \begin 3x+y = 5 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin 3x+(x+1) = 5 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin 4x = 5-1 \\ y = x+1 \end \right.> \Rightarrow $$ $$ \Rightarrow <\left\< \begin x = 1 \\ y = x+1 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 2\end \right.> $$

Примеры

Пример 1. Решите систему уравнений методом подстановки:

$ а) <\left\< \begin 5x-4y = 3 \\ 2x-3y = 4 \end \right.> \Rightarrow <\left\< \begin 5x-4y = 3 \\ x = \frac<3y+4> <2>= 1,5y+2 \end \right.> \Rightarrow <\left\< \begin 5(1,5y+2)-4y = 3 \\ x = 1,5y+2 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 7,5y+10-4y = 3 \\ x=1,5y+2 \end \right.> \Rightarrow <\left\< \begin 3,5y = -7 \\ x = 1,5y+2 \end \right.> \Rightarrow <\left\< \begin y = -2 \\ x = 1,5y+2 \end \right.> \Rightarrow <\left\< \begin x = -1 \\ y = -2\end \right.> $

$ б) <\left\< \begin 4x-3y = 7 \\ 3x-4y = 0 \end \right.> \Rightarrow <\left\< \begin 4x-3y = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow <\left\< \begin 4x-3\cdot \frac<3> <4>x = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow <\left\< \begin (4- \frac<9><4>)x = 7 \\ y = \frac<3> <4>x \end \right.> \Rightarrow $

$\Rightarrow <\left\< \begin x = 7 \cdot \frac<4> <7>= 4 \\ y = \frac<3> <4>x = \frac<3> <4>\cdot 4 = 3 \end \right.> \Rightarrow <\left\< \beginx = 4 \\ y = 3 \end \right.> $

$ в) <\left\< \begin 5a-4b = 9 \\ 2a+3b = -1 \end \right.> \Rightarrow <\left\< \begin 5a-4b = 9 \\ a = \frac<-3b-1> <2>= -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin 5(-1,5b-0,5)-4b = 9 \\ a = -1,5b-0,5 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin -7,5b-2,5-4b = 9 \\ a = -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin-11,5b = 11,5 \\ a = -1,5b-0,5 \end \right.> \Rightarrow <\left\< \begin a = 1 \\ b = -1 \end \right.> $

$ г) <\left\< \begin 7a+4b = 5 \\ 3a+2b = 1 \end \right.> \Rightarrow <\left\< \begin 7a+4b = 5 \\ b = \frac<-3a+1> <2>= -1,5a+0,5 \end \right.> \Rightarrow <\left\< \begin 7a+4(-1,5a+0,5) = 5 \\ b = -1,5a+0,5 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 7a-6a+2 = 5 \\ b = -1,5a+0,5 \end \right.> \Rightarrow <\left\< \begin a = 3 \\ b = -1,5\cdot3+0,5 = -4 \end \right.> $

Пример 2. Найдите решение системы уравнений:

$а) <\left\< \begin \frac<4>-y = 7 | \times 4 \\ 3x+ \frac <2>= 9 | \times 2\end \right.> \Rightarrow <\left\< \begin x-4y = 28 \\ 6x+y = 18 \end \right.> \Rightarrow <\left\< \begin x = 4y+28 = 4(y+7) \\ 6 \cdot 4(y+7)+y = 18 \end \right.> \Rightarrow $

$\Rightarrow <\left\< \begin x = 4(y+7) \\ 24y+168+y = 18 \end \right.> \Rightarrow <\left\< \begin x = 4(y+7) \\ 25y = -150 \end \right.> \Rightarrow <\left\< \beginx = 4(-6+7) = 4 \\ y = -6 \end \right.>$

$ в) <\left\< \begin 3(5x-y)+14 = 5(x+y) \\ 2(x-y)+9 = 3(x+2y)-16 \end \right.> \Rightarrow <\left\< \begin 15x-3y+14 = 5x+5y \\ 2x-2y+9 = 3x+6y-16 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin 10x-8y = -14 |:2 \\ x+8y = 25 \end \right.> \Rightarrow <\left\< \begin 5x-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin 5(-8y+25)-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow $

$ \Rightarrow <\left\< \begin -40y+125-4y = -7 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin -44y = -132 \\ x = -8y+25 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 3 \end \right.> $

$ г) <\left\< \begin 5-3(2x+7y) = x+y-52 \\ 4+3(7x+2y) = 23x \end \right.> \Rightarrow <\left\< \begin 5-6x-21y = x+y-52 \\ 4+21x+6y = 23x \end \right.> \Rightarrow <\left\< \begin 7x+22y = 57 \\ 2x-6y = 4 |:2 \end \right.>$

$$ \Rightarrow <\left\< \begin 7x+22y = 57 \\ x-3y = 2 \end \right.> \Rightarrow <\left\< \begin 7x+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin 7(3y+2)+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin 21y+14+22y = 57 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin 43y = 43 \\ x = 3y+2 \end \right.> \Rightarrow <\left\< \begin x = 5 \\ y = 1 \end \right.>$$

Пример 3*. Найдите решение системы уравнений:

Перепишем систему и найдём решение для новых переменных:

$$ <\left\< \begin 3a+8b = 5 \\ 12b-a = 2 \end \right.> \Rightarrow <\left\< \begin 3(12b-2)+8b = 5 \\ a = 12b-2 \end \right.> \Rightarrow <\left\< \begin 36b-6+8b = 5 \\ a = 12b-2 \end \right.> \Rightarrow $$

Системы линейных уравнений с двумя переменными. Часть 1. Метод подстановки для решения системы линейных уравнений с двумя переменными

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

Мы научились составлять математическую модель для решения различных прикладных задач. В результате задача сводится к технике – решению уравнения или системы уравнений. На этом уроке мы научимся решать системы уравнений, а именно системы линейных уравнений с двумя переменными.