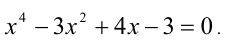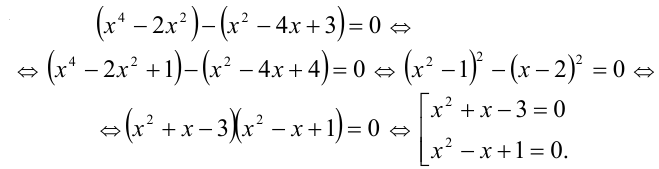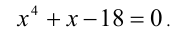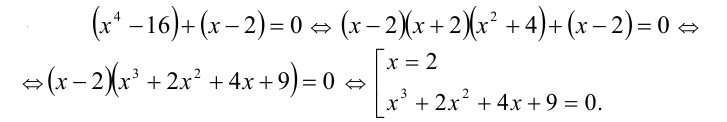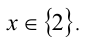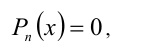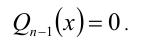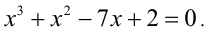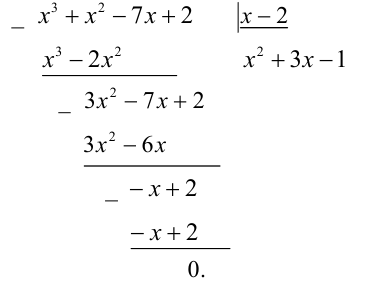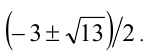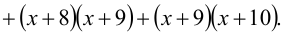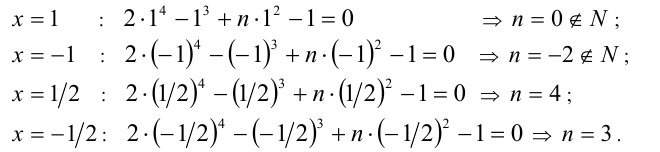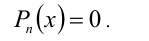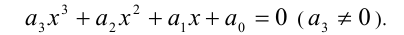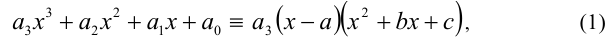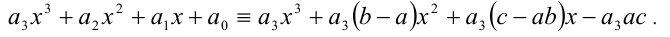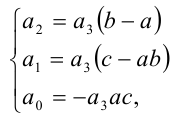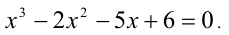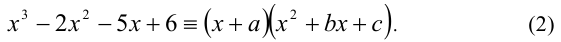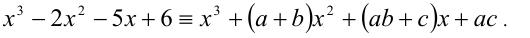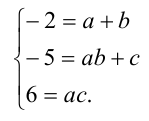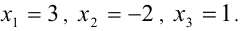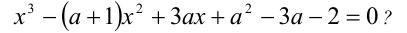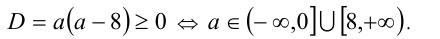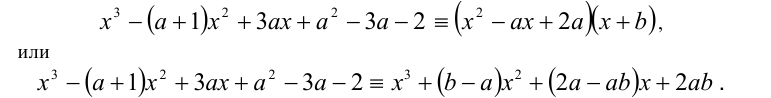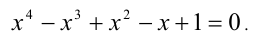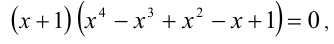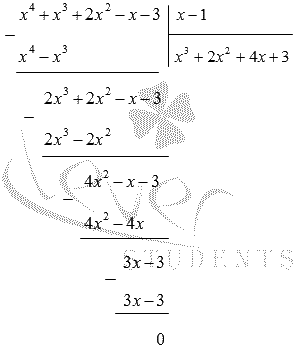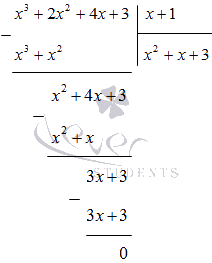Как решать целые уравнения с целыми коэффициентами

Методы решения целых алгебраических уравнений

Методы решения целых алгебраических уравнений

Разложение на множители

Часть целых алгебраических уравнений 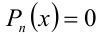(или аналогичных неравенств) степени n выше 2-й могут быть решены путём разложения многочлена в левой части уравнения (неравенства) на множители с помощью таких известных приёмов, как группировка и вынесение общего множителя за скобки. Иногда для достижения цели приходится прибавлять и одновременно вычитать одно и то же выражение. Отметим, что порой разложение на множители этим способом требует определённого искусства.

Если разложение на множители удалось выполнить, то решение алгебраического уравнения сводится к решению совокупности нескольких уравнений, но более низкой степени. Неравенство после разложения на множители можно решать методом интервалов.

Пример №176.

Решить уравнение

Решение:

Из 1-го уравнения находим корни 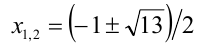, а второе не имеет решений.

Пример №177.

Найти все положительные корни уравнения

Решение:

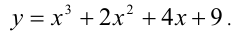
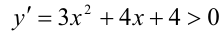
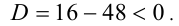
Покажем, что второе уравнение в совокупности не имеет положительных решений. Действительно, рассмотрим функцию Её производная при всех действительных x, так как Следовательно, функция всюду монотонно возрастает, при этом y(0) = 5 . Отсюда следует, что при x > 0 её график не пересекает оси абсцисс.

Ответ:

Подбор корня с последующим понижением степени уравнения

При решении алгебраических уравнений и неравенств степени выше второй можно использовать общий принцип последовательного понижения степени уравнения (неравенства).

Пусть требуется решить уравнение n -й степени

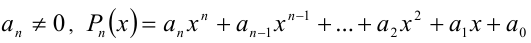
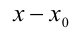
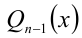
где целый рациональный алгебраический многочлен n -й степени. Если удалось подобрать (любым способом) какой-либо корень данного уравнения, то для нахождения остальных корней уравнения следует поделить многочлен на разность X — Х0 (или целенаправленной группировкой слагаемых, выделяя разность , разложить этот многочлен на множители). В результате деления образуется некоторый многочлен , степень которого на единицу меньше первоначальной. Таким образом, задача свелась к решению алгебраического уравнения степени n — 1 :

Пример №178.

Решить уравнение

Решение:

Заметим, что x = 2 является корнем данного уравнения. Найдём другие корни этого уравнения:

Решая уравнение 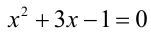, находим ещё два корня

Эта ссылка возможно вам будет полезна:

Пример №179.

Решить уравнение

Решение:

Легко заметить, проанализировав структуру уравнения, что числа x = 0 и x = -10 являются решениями данного уравнения. С другой стороны, ясно, что это квадратное уравнение, а поэтому может иметь не более двух корней. Так как два корня уравнения уже подобраны, то других корней нет.

В некоторых случаях, для того чтобы не подбирать корень «вслепую», можно воспользоваться следующим методом.

Метод поиска рациональных корней у многочленов с целыми коэффициентами

Для решения такого рода уравнений и неравенств используется метод, в основе которого лежит Теорема 9 из предыдущего пункта. Рассмотрим подробнее суть этого метода. Пусть требуется найти рациональные корни уравнения n -й степени

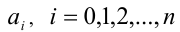
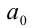
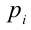
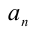
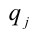
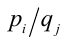
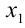
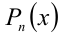
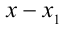
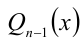
причём все коэффициенты алгебраического многочлена являются целыми числами. Поиск рациона-льных корней можно свести к перебору ограниченного количества вариантов. Для этого необходимо, во-первых, найти все целочислен-ные делители свободного члена (их конечное число, однако если этот коэффициент содержит слишком много делителей, то это затрудняет поиск корней в уравнении). Обозначим, например, эти делители через . Во-вторых, следует найти все натуральные делители старшего коэффициента уравнения . Обозначим эти делители через . В-третьих, надо составить всевозможные дроби вида . Наконец, перебирая по очереди все такие дроби, проверить, является ли в действительности каждая из них корнем данного уравнения. Найдя таким образом первый корень , вы или сразу понижаете степень уравнения делением многочлена на разность , (причём в силу следствия из теоремы Безу обязательно разделится нацело на этот линейный двучлен) и получаете некоторый многочлен степени на единицу меньшей, чем первоначальная. Или, перебирая все дроби, находите все рациональные корни и уже затем понижаете степень уравнения сразу на столько порядков, сколько рациональных корней удалось найти, и ищете оставшиеся иррациональные корни. В любом случае задача сводится к решению уравнения более низкой степени.

Пример №180.

При каких натуральных n уравнение 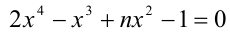имеет рациональные корни?

Решение:

Воспользуемся приведённым выше методом. Свободный член имеет два целочисленных делителя: ± 1, а старший коэффициент — два натуральных делителя: 1,2. Поэтому рациональные корни следует искать среди чисел 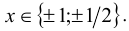Подставим их поочерёдно в уравнение.

Ответ:

Метод неопределённых коэффициентов

Иногда для решения целых алгебраических уравнений (неравенств) с одной или несколькими неизвестными используют метод неопределённых коэффициентов. Пусть, например, решается уравнение

Суть метода состоит в том, что многочлен в левой части уравнения представляется в виде произведения линейных и(или) квадратичных сомножителей с неизвестными (неопределёнными) коэффициентами Чтобы найти эти коэффициенты, раскрывают скобки в указанном произведении и приводят образовавшийся при этом многочлен к стандарт-ному виду. Так как два многочлена и одной степени тождественно равны тогда и только тогда,

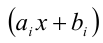
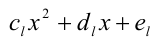
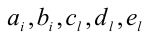
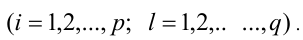
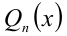
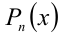
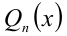
когда равны коэффициенты при одинаковых степенях переменной x, то, приравнивая эти коэффициенты, получают систему уравнений относительно неизвестных коэффициентов. Эту систему решают (или подбирают любое решение). Найденные таким способом коэффи-циенты 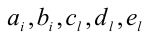становятся определёнными и их значения подставляются в исходное разложение. К недостаткам метода можно отнести то, что получаемая система уравнений для нахождения коэффициентов может оказаться громоздкой и трудной даже в подборе решения.

Рассмотрим применение этого метода на примере решения кубического уравнения. Допустим, требуется решить уравнение

Известно, что многочлен третьей степени всегда можно представить в виде произведения многочленов первой и второй степеней. Таким образом, сразу для всех действительных значений переменной x должно выполняться равенство

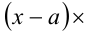
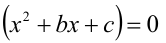
где числа а,b,c являются в данном случае искомыми неопределён-ными коэффициентами. Найдём их значения. После этого останется подставить их в правую часть (1) и, приравняв её к нулю, решить уравнение для нахождения всех корней уравнения.

Чтобы найти коэффициенты а,b,c, раскроем скобки в правой части тождества (1) и приведём образовавшийся при этом многочлен к стандартному виду

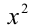
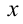
Многочлены третьей степени тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях x . Приравнивая коэффициенты при , и свободные члены, получаем систему трёх алгебраических уравнений относительно трёх неизвестных а,b,c :

решая которую (можно даже просто подобрать любое решение этой системы) находим коэффициенты.

Пример №181.

Решить уравнение

Решение:

Воспользуемся для решения методом неопределённых коэффициентов. Будем искать разложение многочлена, стоящего в левой части уравнения, в виде

Раскрыв скобки, приведём многочлен в правой части к стандартному виду

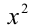
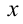
Приравнивая коэффициенты слева и справа при ,и свободные члены, получаем в итоге систему трёх уравнений с тремя неизвестными коэффициентами а,b,c:

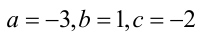
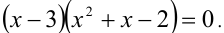
Найдя подбором решение подставим найденные коэффициенты в разложение (2). Таким образом, исходное уравнение приобретает вид Оно имеет три корня

Пример №182.

При каких значениях а все корни уравнения 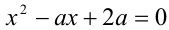являются корнями уравнения

Решение:

Чтобы первое из уравнений имело корни, необходимо, чтобы его дискриминант был неотрицателен, т.е.

Далее, второй многочлен в силу теоремы Безу должен делиться нацело на первый многочлен. Иными словами, должно найтись такое b , что при всех действительных x справедливо тождество

Для нахождения неопределённых коэффициентов (в данном случае в их роли выступают а и b ) воспользуемся известным фактом, что два кубических многочлена, стоящие по разные стороны от знака равенства, тождественно равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной x . Приравнивая эти коэффициенты, получаем систему уравнений

Метод умножения на функцию

Иногда, применяя приём умножения обеих частей уравнения (неравенства) на некоторую функцию, удаётся упростить уравнение (неравенство).

Пример №183.

Решить уравнение

Решение:

Заметим, что x = — 1 (и вообще никакое отрицательное число) не является корнем данного уравнения. Домножим обе части данного уравнения на выражение (х +1). Получаем уравнение-следствие

множество решений которого состоит из всех решений исходного уравнения и числа x = -1. Это число является посторонним корнем, возникшем как раз в результате умножения уравнения на функцию, имеющую действительный нуль. Применяя известную формулу сокращенного умножения, получаем существенно более простое уравнение 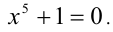Поскольку уравнение не имеет других решений, кроме x = -1, то приходим к ответу.

Ответ: уравнение не имеет решений.

Рассмотрим некоторые виды целых алгебраических уравнений, решаемые в основном при помощи специально подобранных подстановок.

Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Эти страницы возможно вам будут полезны:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Как решать целые уравнения с целыми коэффициентами

Объект исследования.

Исследования касаются одного из наиболее интересных разделов теории чисел — решения уравнений в целых числах.

Предмет исследования.

Решение в целых числах алгебраических уравнений с целыми коэффициентами более чем с одним неизвестным представляет собой одну из труднейших и древнейших математических задач и не достаточно глубоко представлена в школьном курсе математики. В своей работе я представлю достаточно полный анализ уравнений в целых числах, классификацию данных уравнений по способам их решения, описание алгоритмов их решения, а также практические примеры применения каждого способа для решения уравнений в целых числах.

Цель.

Познакомиться со способами решения уравнений в целых числах.

Задачи:

Изучить учебную и справочную литературу;

Собрать теоретический материал по способам решения уравнений;

Разобрать алгоритмы решения уравнений данного вида;

Описать способы решения;

Рассмотреть примеры решения уравнений с применением данных способов.

Гипотеза:

Столкнувшись с уравнениями в целых числах в олимпиадных заданиях, я предположила, что трудности в их решении обусловлены тем, что далеко не все способы их решения мне известны.

Актуальность:

Решая примерные варианты заданий ЕГЭ, я заметила, что часто встречаются задания на решение уравнений первой и второй степени в целых числах. Кроме того олимпиадные задания различных уровней также содержат уравнения в целых числах или задачи, которые решаются с применением умений решать уравнения в целых числах. Важность знания способов решения уравнений в целых числах и определяет актуальность моих исследований.

Методы исследования

Теоретический анализ и обобщение сведений научной литературы об уравнениях в целых числах.

Классификация уравнений в целых числах по методам их решения.

Анализ и обобщение методов решения уравнений в целых числах.

Результаты исследования

В работе описаны способы решений уравнений, рассмотрен теоретический материал теоремы Ферма, теорема Пифагора, алгоритма Евклида, представлены примеры решений задач и уравнений различных уровней сложности.

2.История уравнений в целых числах

Диофант – ученый – алгебраист Древней Греции, по некоторым данным он жил до 364 года н. э. Он специализировался на решении задач в целых числах. Отсюда и пошло название Диофантовы уравнения. Наиболее известной, решенной Диофантом, является задача «о разложении на два квадрата». Ее эквивалентом является известная всем теорема Пифагора. Жизнь и деятельность Диофанта протекала в Александрии, он собирал и решал известные и придумывал новые задачи. Позднее он объединил их в большом труде под названием «Арифметика». Из тринадцати книг, входивших в состав «Арифметики», только шесть сохранились до Средних веков и стали источником вдохновения для математиков эпохи Возрождения.«Арифметика» Диофанта — это сборник задач, каждая включает в себя решение и необходимое пояснение. В собрание входят разнообразные задачи, а их решение часто в высшей степени остроумно. Диофанта интересуют только положительные целые и рациональные решения. Иррациональные решения он называет «невозможными» и тщательно подбирает коэффициенты так, чтобы получились искомые положительные, рациональные решения.

Для решения уравнений в целых числах применяется теорема Ферма. История доказательства которой достаточно интересная. Над полным доказательством Великой теоремы работало немало выдающихся математиков, и эти усилия привели к получению многих результатов современной теории чисел. Считается, что теорема стоит на первом месте по количеству неверных доказательств.

Замечательный французский математик Пьер Ферма высказал утверждение, что уравнение при целом n ≥ 3 не имеет решений в целых положительных числах x, y, z ( xyz = 0 исключается положительностью x, y, z.Для случая n = 3 эту теорему в X веке пытался доказать среднеазиатский математик ал-Ходжанди, но его доказательство не сохранилось. Несколько позже сам Ферма опубликовал доказательство частного случая для n = 4.

Эйлер в 1770 доказал теорему для случая n = 3, Дирихле и Лежандр в 1825 — для n = 5,Ламе — для n = 7. Куммер показал, что теорема верна для всех простых n, меньших 100, за возможным исключением 37, 59, 67.

В 1980-х годах появился новый подход к решению проблемы. Из гипотезы Морделла, доказанной Фальтингсом в 1983 году, следует, что уравнение

при n > 3 может иметь лишь конечное число взаимно простых решений.

Последний, но самый важный, шаг в доказательстве теоремы был сделан в сентябре 1994 года Уайлсом. Его 130-страничное доказательство было опубликовано в журнале «AnnalsofMathematics». Доказательство основано на предположении немецкого математика Герхарда Фрая о том, что Великая теорема Ферма является следствием гипотезы Таниямы — Симуры (это предположение было доказано Кеном Рибетом при участии Ж.‑П.Серра. ).Первый вариант своего доказательства Уайлс опубликовал в 1993 году (после 7 лет напряжённой работы), но в нём вскоре обнаружился серьёзный пробел; с помощью Ричарда Лоуренса Тейлора пробел удалось достаточно быстро ликвидировать. В 1995 году был опубликован завершающий вариант. 15 марта 2016 года Эндрю Уайлз получает премию Абеля. В настоящее время премия составляет 6 миллионов норвежских крон, то есть примерно 50 миллионов рублей. По словам Уайлса, присуждение премии стало для него «полной неожиданностью».

3.Линейные уравнения в целых числах

Линейные уравнения – самые простые из всех диофантовых уравнений .

Уравнение вида ах=b, где a и b – некоторые числа, а х- неизвестная переменная, называется линейным уравнением с одной неизвестной. Здесь требуется найти только целые решения уравнения. Можно заметить, что если а ≠ 0, то целочисленное решение уравнение будет иметь только в том случае, когда b нацело делится на а и это решение х= b/ф. Если же а=0, то целочисленное решение уравнение будет иметь тогда, когда b=0 и в этом случае х любое число.

т.к. 12 нацело делится на 4, то

Т.к. а=о и b=0, то х любое число

Т.к. 7 нацело не делится на 10, то решений нет.

4. Способ перебора вариантов.

В способе перебора вариантов необходимо учитывать признаки делимости чисел, рассмотреть все возможные варианты равенства конечного перебора. Этот способ можно применить решая данные задачи:

№1 Найти множество всех пар натуральных чисел, которые являются решением уравнения 49x+69y=602

Выражаем из уравнения х =,

Т.к. x и y натуральные числа, то х = ≥ 1, умножаем все уравнение на 49, чтобы избавиться от знаменателя:

Переносим 602 в левую сторону:

51y ≤ 553, выражаем y, y= 10

Полный перебор вариантов показывает, что натуральными решениями уравнения являются x=5, y=7.

№2 Решить задачу

Из цифр 2, 4, 7 следует составить трёхзначное число, в котором ни одна цифра не может повторяться более двух раз.

Найдем количество всех трехзначных чисел, которые начинаются с цифры 2: (224, 242, 227, 272, 247, 274, 244, 277) – их 8.

Аналогично находим все трехзначные цифры начинающиеся с цифр 4 и 7: (442, 424, 422, 447, 474, 427, 472, 477).

(772, 774, 727, 747, 722, 744, 724, 742) – их тоже по 8 чисел. Следует всего 24 числа.

5. Цепная дробь и алгоритм Евклида

Цепной дробью называется выражение обыкновенной дроби в виде

где q₁ – целое число, а q₂, … ,qn – натуральные числа. Такое выражение называется цепной (конечной непрерывной) дробью. Различают конечные и бесконечные цепные дроби.

Для рациональных чисел цепная дробь имеет конечный вид. Кроме того, последовательность a_i— это ровно та последовательность частных, которая получается при применении алгоритма Евклида к числителю и знаменателю дроби.

Решая уравнения цепной дробью, я составила общий алгоритм действий для данного способа решения уравнений в целых числах.

Алгоритм

1) Составить отношение коэффициентов при неизвестных в виде дроби

2) Преобразовать выражение в неправильную дробь

3) Выделить целую часть неправильной дроби

4) Правильную дробь заменить равной ей дробью

5) Проделать 3,4 с полученной в знаменателе неправильной дробью

6) Повторять 5 до конечного результата

7) У полученного выражения отбросить последнее звено цепной дроби, превратить получающуюся при этом новую цепную дробь в простую и вычесть ее из исходной дробь.

Пример №1 Решить в целых числах уравнение 127x- 52y+ 1 = 0

Преобразуем отношение коэффициентов при неизвестных.

Прежде всего, выделим целую часть неправильной дроби ; = 2 +

Правильную дробь заменим равной ей дробью .

Проделаем такие же преобразования с полученной в знаменателе неправильной дробью.

Теперь исходная дробь примет вид: .Повторяя те же рассуждения для дроби получим Выделяя целую часть неправильной дроби, придем к окончательному результату:

Мы получили выражение, которое называется конечной цепной или непрерывной дробью. Отбросив последнее звено этой цепной дроби — одну пятую, превратим получающуюся при этом новую цепную дробь в простую и вычтем ее из исходной дроби :

Приведем полученное выражение к общему знаменателю и отбросим его.

Откуда 127∙9–52∙22+1=0. Из сопоставления полученного равенства с уравнением 127x- 52y+1 = 0 следует, что тогда x= 9, y= 22 — решение исходного уравнения, и согласно теореме все его решения будут содержаться в прогрессиях x= 9+ 52t, y= 22+ 127t, где t=( 0; ±1; ±2…..).Полученный результат наводит на мысль о том, что и в общем случае для нахождения решения уравнения ax+by+c=0 надо разложить отношение коэффициентов при неизвестных в цепную дробь, отбросить ее последнее звено и проделать выкладки, подобные тем, которые были приведены выше.

Для доказательства этого предположения будут нужны некоторые свойства цепных дробей.

Рассмотрим несократимую дробь . Обозначим через q₁ частное и через r₂ остаток от деления a на b. Тогда получим:

Пусть, далее, q₂ – частное и r₃ – остаток от деления b на r₂.

Величины q₁, q₂,… называются неполными частными. Приведенный выше процесс образования неполных частных называется алгоритмом Евклида. Остатки от деления r₂, r₃,…удовлетворяют неравенствам

т.е. образуют ряд убывающих неотрицательных чисел.

Пример№2 Решить уравнение170х+190у=3000 в целых числах

После сокращения на 10 уравнение выглядит так,

Для нахождения частного решения воспользуемся разложением дроби в цепную дробь

Свернув предпоследнюю подходящую к ней дробь в обыкновенную

Частное решение данного уравнения имеет вид

а общее задается формулой

х=2700-19k, y= -2400+17k.

откуда получаем условие на параметр k

6. Метод разложения на множители

Метод перебора вариантов неудобный способ, так как бывают случаи когда найти перебором всецелые решения, невозможно, так как таких решений бесконечное множество. Метод разложения на множители очень интересный прием и встречается он как и в элементарной математике так и в высшей.

Суть состоит в тождественном преобразовании. Смысл любого тождественного преобразования — это запись выражения в другом виде с сохранением его сути. Рассмотрим примеры применения данного метода.

№1 Решить уравнение в целых числах y 3 — x 3 = 91.

Используя формулы сокращенного умножения, разложим правую часть уравнения на множители:

(y — x)(y 2 + xy + x 2 ) = 91

Выписываем все делители числа 91: ± 1; ± 7; ± 13; ± 91

Замечаем, что для любых целых x и y число

y 2 + yx + x 2 ≥ y 2 — 2|y||x| + x 2 = (|y| — |x|) 2 ≥ 0,

следовательно, оба сомножителя в левой части уравнения должны быть положительными. Тогда исходное уравнение равносильно совокупности систем уравнений:

Решив системы, отбираем те корни, которые являются целыми числами.

Получаем решения исходного уравнения: (5; 6), (-6; -5); (-3; 4),(-4;3).

№2 Найти все пары натуральных чисел, удовлетворяющих уравнению х 2 –у 2 = 69

Разложим левую часть уравнения на множители и запишем уравнение в виде

Т.к. делителями числа 69 являются числа 1, 3, 23 и 69, то 69 можно получить двумя способами: 69=1·69 и 69=3·23. Учитывая, что х-у > 0, получим две системы уравнений, решив которые мы сможем найти искомые числа:

Выразив одну переменную и подставив ее в второе уравнение находим корни уравнений.Первая система имеет решение x=35;y=34 , а вторая система имеет решение x=13, y=10.

Ответ: (35; 34), (13; 10).

№3 Решить уравнение х+у =ху в целых числах:

Запишем уравнение в виде

Разложим левую часть уравнения на множители. Получим

Произведение двух целых чисел может равняться 1 только в двух случаях: если оба они равны 1 или -1. Получим две системы:

Первая система имеет решение х=2, у=2, а вторая система имеет решение х=0, у=0.Ответ: (2; 2), (0; 0).

№4 Доказать, что уравнение (x — y) 3 + (y — z) 3 + (z — x) 3 = 30 не имеет решений в целых числах.

Разложим левую часть уравнения на множители и обе части уравнения разделим на 3, в результате получим уравнение:

( x — y)(y — z)(z — x) = 10

Делителями 10 являются числа ±1, ±2, ±5, ±10. Заметим также, что сумма сомножителей левой части уравнения равна 0. Нетрудно проверить, что сумма любых трех чисел из множества делителей числа 10, дающих в произведении 10, не будет равняться 0. Следовательно, исходное уравнение не имеет решений в целых числах.

7. Метод остатков

Основная задача метода — находить остаток от деления обоих частей уравнения на целое число, на основе полученных результатов. Часто полученная информация уменьшает возможности множеств решений уравнения. Рассмотрим примеры:

№1 Доказать, что уравнение x 2 = 3y + 2 не имеет решений в целых числах.

Рассмотрим случай, когда x, y ∈ N. Рассмотрим остатки от деления обоих частей на 3. Правая часть уравнения дает остаток 2 при делении на 3 при любом значении y. Левая же часть, которая является квадратом натурального числа, при делении на 3 всегда дает остаток 0 или 1. Исходя из этого получаем, что решения данного уравнения в натуральных числах нет.

Рассмотрим случай, когда одно из чисел равно 0. Тогда очевидно, решений в целых числах нет.

Случай, когда y — целое отрицательное не имеет решений, т.к. правая часть будет отрицательна, а левая — положительна.

Случай, когда x — целое отрицательное, также не имеет решений, т.к. попадает под один из рассмотренных ранее случаев ввиду того, что (-x) 2 = (x) 2 .

Получается, что указанное уравнение не имеет решений в целых числах, что и требовалось доказать.

№2 Решите в целых числах 3 х = 1 + y 2 .

Не сложно заметить, что (0; 0) — решение данного уравнения. Остаётся доказать, что других целых корней уравнение не имеет.

1) Если x∈N, y∈N, то З делится на три без остатка, а 1 + y 2 при делении на 3 дает

остаток либо 1, либо 2. Следовательно, равенство при натуральных

значениях х, у невозможно.

2) Если х— целое отрицательное число,y∈Z , тогда 0 х 2 ≥ 0 и

равенство также невозможно. Следовательно, (0; 0) — единственное

№3 Решить уравнение 2х 2 -2ху+9х+у=2 в целых числах:

Выразим из уравнения то неизвестное, которое входит в него только в первой степени, то есть переменную у:

2х 2 +9х-2=2ху-у, откуда

Выделим у дроби целую часть с помощью правила деления многочлена на многочлен «углом». Получим:

Очевидно, разность 2х-1 может принимать только значения -3, -1, 1 и 3.

Осталось перебрать эти четыре случая, в результате чего получаем решения: (1;9), (2;8), (0;2), (-1;3)

8.Пример решения уравнений с двумя переменными в целых числах как квадратных относительно одной из переменных

№1 Решить в целых числах уравнение 5х 2 +5у 2 + 8ху+2у-2х +2=0

Данное уравнение можно решить методом разложения на множители, однако этот способ применительно к данному уравнению достаточно трудоёмкий. Рассмотрим более рациональный способ.

Запишем уравнение в виде квадратного относительно переменной х:

5x 2 +(8y-2)x+5y 2 +2y+2=0

Находим его корни.

Данное уравнение имеет решение тогда и только тогда, когда дискриминант

этого уравнения равен нулю, т.е. — 9(у+1) 2 =0, отсюда у= — 1.

9.Пример решения задач с помощью уравнений в целых числах.

№ 1. Решить в натуральных числах уравнение: где n>m

Выразим переменную n через переменную m:

Найдем делители числа 625: это 1; 5; 25; 125; 625

1) если m-25 =1, то m=26, n=25+625=650

2) m-25 =5, то m=30, n=150

3) m-25 =25, то m=50, n=50

4) m-25 =125, то m=150, n=30

5) m-25 =625, то m=650, n=26

№ 2. Решить уравнение в натуральных числах: mn +25 = 4m

Решение: mn +25 = 4m

1) выразим переменную 4m через n:

2) найдем натуральные делители числа 25: это 1; 5; 25

если 4-n =1, то n=3, m=25

4-n=5, то n=-1, m=5; 4-n =25, то n=-21, m=1 (посторонние корни)

Помимо заданий решить уравнение в целых числах, встречаются задания на доказательство того факта, что уравнение не имеет целых корней.

При решении таких задач, необходимо помнить следующие свойства делимости:

1) Если n Z; n делится на 2, то n = 2k, k ∈ Z.

2) Если n ∈ Z; n не делится на 2, то n = 2k+1, k ∈ Z.

3) Если n ∈ Z; n делится на 3, то n = 3k, k ∈ Z.

4) Если n ∈ Z; n не делится на 3, то n = 3k±1, k ∈ Z.

5) Если n ∈ Z; n не делится на 4, то n = 4k+1; n = 4k+2; n = 4k+3. k ∈ Z.

6) Если n ∈ Z; n(n+1) делится на 2, то n (n+1)(n+2) делится на 2;3;6.

7) n; n+1 – взаимно простые.

№3 Доказать, что уравнение x 2 – 3у = 17 не имеет целых решений.

Пусть x; y – решения уравнения

x 2 = 3(у+6)-1 Т.к. y ∈ Z то y+6 ∈ Z , значит 3(y+6) делится на 3, следовательно, 3(y+6)-1 не делится на 3, следовательно, x 2 не делится на 3, следовательно, x не делится на 3, значит x = 3k±1, k ∈ Z.

Подставим это в исходное уравнение.

Получили противоречие. Значит у уравнения нет целых решений, что и требовалось доказать.

10.Формула Пика

Формула Пика была открыта австрийским математиком Георгом Пиком в 1899 году. Формула связанна с уравнениями в целых числах тем, что из многоугольников берут только целые узлы, как и целые числа в уравнениях.

При помощи этой формулы можно находить площадь фигуры построенной на листе в клетку (треугольник, квадрат, трапеция, прямоугольник, многоугольник).

В этой формуле будем находить целые точки внутри многоугольника и на его границе.

В задачах, которые будут на ЕГЭ есть целая группа заданий, в которых дан многоугольник построенный на листе в клетку и стоит вопрос о нахождении площади. Масштаб клетки это один квадратный сантиметр.

М – количество узлов на границе треугольника (на сторонах и вершинах)

N – количество узлов внутри треугольника.

*Под «узлами» имеется ввиду пересечение линий. Найдём площадь треугольника:

M = 15 (обозначены красным)

N = 34 (обозначены синим)

Найдём площадь многоугольника: Отметим узлы:

M = 14 (обозначены красным)

N = 43 (обозначены синим)

12.Метод спуска

Один из методов решений уравнений в целых числах – метод спуска — опирается на теорему Ферма.

Методом спуска называется метод, который заключается в построении одного решения бесчисленной последовательности решений с неограниченно убывающим положительным z.

Алгоритм этого метода рассмотрим на примере решения конкретного уравнения.

Пример 1. Решить уравнение в целых числах 5x + 8y = 39.

1) Выберем неизвестное, имеющее наименьший коэффициент (в нашем случае это х), и выразим его через другое неизвестное:

2) Выделим целую часть: Очевидно, что х будет целым, если выражение окажется целым, что, в свою очередь, будет иметь место тогда, когда число 4 – 3y без остатка делится на 5.

3) Введем дополнительную целочисленную переменную z следующим образом: 4 –3y = 5z. В результате получим уравнение такого же типа, как и первоначальное, но уже с меньшими коэффициентами.

4) Решаем его уже относительно переменной y, рассуждая точно также как в п.1, 2: Выделяя целую часть, получим:

5) Рассуждая аналогично предыдущему, вводим новую переменную u: 3u = 1 – 2z.

6) Выразим неизвестную с наименьшим коэффициентом, в этом случае переменную z: . Требуя, чтобы было целым, получим: 1 – u = 2v, откуда u = 1 – 2v. Дробей больше нет, спуск закончен (процесс продолжаем до тез пор, пока в выражении для очередной переменной не останется дробей).

7) Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x:

8) Формулы x = 3+8v и y = 3 – 5v, где v – произвольное целое число, представляют общее решение исходного уравнения в целых числах.

Таким образом, метод спуска предполагает сначала последовательное выражение одной переменой чрез другую, пока в представлении переменной не останется дробей, а затем, последовательное «восхождение» по цепочке равенств для получения общего решения уравнения.

12.Заключение

В результате исследования подтвердилась гипотеза о том, что трудности при решении уравнений в целых числах обусловлены тем, что далеко не все способы их решения были мне известны. В ходе исследований мне удалось отыскать и описать малоизвестные способы решения уравнений в целых числах, проиллюстрировать их примерами. Результаты моих исследований могут быть полезны всем ученикам, интересующимся математикой.

13.Библиография

Книжные ресурсы:

1. Н. Я. Виленкин и др., Алгебра и математический анализ/10класс, 11 класс// М., «Просвещение», 1998 год;

2. А. Ф. Иванов и др., Математика. Учебно-тренировочные материалы для подготовки к экзамену// Воронеж, ГОУВПО ВГТУ, 2007 год

3. А. О. Гельфонд, Математика, теория чисел// Решение уравнений в целых числах// Книжный дом «ЛИБРОКОМ»

Ресурсы сети интернет:

Решение уравнений высших степеней

В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.

Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.

Уравнения высшей степени с целыми коэффициентами

Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :

a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0

Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .

Схема решения уравнения

Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .

Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .

Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.

Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.

У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.

Покажем на конкретном примере, как применяется такая схема решения.

Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .

Решение

Начнем с нахождений целых корней.

У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.

При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.

Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:

Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .

Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :

1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0

У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .

Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:

x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )

Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :

— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0

Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.

Оставшиеся корни будут корнями выражения x 2 + x + 3 .

D = 1 2 — 4 · 1 · 3 = — 11 0

Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .

Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.

В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .

После нахождения следующего корня, равного — 1 , мы получаем следующее:

Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.

Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .

Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .

Решение

У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .

Проверяем их по порядку:

1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0

Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:

В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .

Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.

2 3 + 2 2 — 3 · 2 — 6 = 0

Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :

В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .

Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.

Решим квадратное уравнение:

x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0

Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .

Ответ: x = — 3 2 ± i 3 2 .

Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.

Решение

x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0

Выполняем домножение 2 3 обеих частей уравнения:

2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0

Заменяем переменные y = 2 x :

2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0

В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .

Ответ: x 1 = — 1 , x 2 = 3 2

Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.