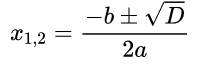Как решать уравнение и неравенства 2 степени

Решение неравенств второй степени

Решение неравенств второй степени

Неравенством второй степени называется неравенство вида ax2 + bx + c > 0 (или ax2 + bx + c 0. Если D > 0, то для решения неравенства ах2 + bх + с > 0 нужно разложить квадратный трехчлен на множители ах2 + bх + с по формуле ах +bх + с = а(х-х1)(х-х2), затем разделить обе части неравенства а(х-х1)(х-х2) > 0 на число а, сохранив знак неравенства, если а>0, и изменив знак неравенства на противоположный, если а 0.
Дальше используют тот факт, что произведение двух чисел положительно, если сомножители имеют одинаковые знаки (если (х-х1)(х-х2) 0.

Р е ш е н и е.
x2 — 5x + 6 = 0 ↔ x1 = 2, x1 = 3 → x2 — 5x + 6 = (x — 2)(x — 3).
Отсюда x2 — 5x + 6 > 0 ↔ (x — 2)(x — 3) > 0 ↔

↔↔ ↔ ↔ x (-;2)(3;).

Ответ: x (-;2)(3;).

Замечание. Рассмотренное выше неравенство второй степени обычно решают либо графически, либо методом интервалов, которые рассмотрены ниже. Однако приведенные выше способы также имеют право на существование, т. к. они достаточно просты и наглядны.

Графическое решение неравенств второй степени:

Графиком квадратичной функции y = ах2 +bх + с является парабола с ветвями, направленными вверх, если а > 0, и вниз, если а 0 и выпуклостью вверх, если а 0.

Р е ш е н и е. Рассмотрим функцию у = x2. Графиком этой функции является парабола, ветви которой направлены вверх (парабола направлена выпуклостью вниз). Парабола пересекает ось Ох в точке с абсциссой х = 0, так как х2 = 0 ↔ х = 0. Изобразив схематически параболу у = x2, найдем, что у > 0 при x (-;0) (0;). На чертеже искомое множество заштриховано.

Ответ: x (-;0) (0;). .

Пример 3. Решить неравенство -2×2 + 3x + 2 > 0.

Р е ш е н и е. Рассмотрим функцию у = -2×2 + 3x + 2. Ее графиком является парабола, ветви которой направлены вниз (парабола направлена выпуклостью вверх), т. к. а = —2

Квадратные неравенства с одной переменной

теория по математике 📈 неравенства

Неравенство вида ax 2 +bx+c>0 или ax 2 +bx+c

Для решения неравенства находят промежутки, в которых функция у=ax 2 +bx+c принимает положительные или отрицательные значения, это зависит от знака неравенства, данного в стандартном виде. Для этого достаточно определить, в каком направлении расположены ветви параболы у=ax 2 +bx+c, а также найти нули данной функции, относительно которых и определяются промежутки.

Вспомним, что ветви параболы направлены вверх при а>0, ветви направлены вниз при а 2 +bx+c.

Алгоритм решения неравенства второй степени с одной переменной

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Проводимость — способность живой ткани проводить возбуждение.

Первый случай. D>0, a>0.

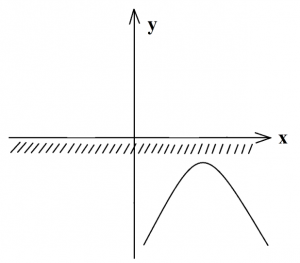
х 2 +2х–48 2 +2х–48:

D=b 2 –4ac=2 2 -=4+192=196>0

Значит, квадратный трехчлен имеет два корня, находим их по формуле:

Это будут числа –8 и 6. Нам надо на оси х отметить две выколотые точки и построить параболу ветвями вверх, так как число а=1, то есть а>0. Теперь для ответа определяем промежуток отрицательных чисел, так как в условии неравенства стоит знак «меньше».

Это будут все числа, расположенные ниже оси х (на рисунке промежуток заштрихован), в ответ запишем промежуток чисел (–8;6).

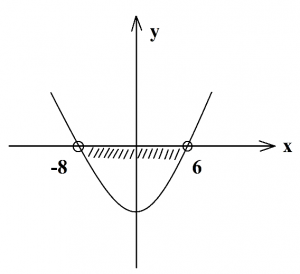
Второй случай. D>0, a 2 +2х+15

Третий случай. D=0, a 2 –12х+9>0

Находим дискриминант, он равен нулю. Значит, имеем

Корень — осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

То есть, это числа от минус бесконечности до 1,5 и от 1,5 до плюс бесконечности, так как точка 1,5 выколотая, а значит, она не входит в данный промежуток чисел. Запишем ответ: (-∞;-1,5)∪(1,5:+∞). Также данный ответ можно записать короче: х≠1,5.

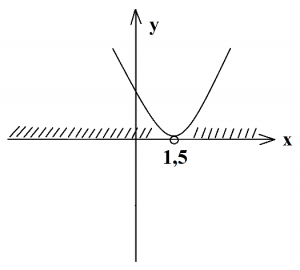
Четвертый случай. D 0.

Пятый случай. D 2 +3х–2≤0

Находим дискриминант, он равен отрицательному числу (–71), значит, корней нет. В координатной плоскости покажем параболу, которая не пересекает ось х, то есть, расположена в нижней полуплоскости ветвями вниз, так как а=–10. Теперь для нахождения ответа определяем промежуток отрицательных чисел: так как парабола находится в нижней полуплоскости, а нам нужен промежуток отрицательных чисел (показан штриховкой), то данное неравенство имеет множество решений (искомый промежуток совпал с расположением параболы в нижней полуплоскости).

Записываем ответ: множество решений. Также ответ можно записать в виде промежутка (-∞;+∞) или записать так: х – любое число.

Для того чтобы начать решать неравенство, мы должны понимать, интервал каких чисел будем находить – положительных или отрицательных. Для этого перенесем выражение из правой части в левую, изменяя знак на противоположный, и справа от знака «меньше» образуется нуль:

( х − 5 ) 2 − √ 7 ( х − 5 ) 0 Теперь вынесем за скобки общий множитель (х-5), получим: ( х − 5 ) ( х − 5 − √ 7 ) 0 Найдем нули функции, приравнивая каждый множитель к нулю: х − 5 = 0 , откуда х=5 х − 5 − √ 7 = 0 , откуда: х = 5 + √ 7 Отметим эти числа на числовом луче и найдем интервал отрицательных чисел: 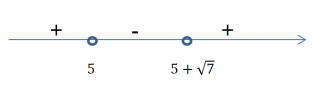Итак, видно, что необходимый интервал от 5 до ( 5 + √ 7 ) Ответ: ( 5 ; 5 + √ 7 ) Ответ: см. решение

pазбирался: Даниил Романович | обсудить разбор | оценить

Имеем дробное неравенство, где решать надо будет только знаменатель. Но для этого посмотрим, что решением неравенства являются числа, которые больше или равны нулю. Для этого наш знаменатель должен быть отрицательным числом, так как числитель – число тоже отрицательное, а при делении двух отрицательных чисел получим число положительное. Далее, знаменатель не должен быть равен нулю, так как на нуль делить нельзя. Следовательно, начнем решение с того, что выпишем знаменатель, который должен быть отрицательным числом:

У нас получилось квадратное неравенство, которое мы и должны решать. Начнем с раскрытия скобок по формуле сокращенного умножения и приведения подобных слагаемых:

Получим квадратное неравенство, для которого надо найти интервал отрицательных чисел ( 0 )

Для этого найдем нули функции, решая с помощью дискриминанта:

Д=(-4) 2 – 4 ∙ 1 ∙ 1 =16-4=12

х 1 = 4 − √ 12 2 . . = 2 ( 2 − √ 3 ) 2 . . = 2 − √ 3

Знаем, что х₂ будет отличаться только знаком, получим, что х 2 = 2 + √ 3 Теперь отмечаем числа на числовом луче и показываем интервалы справа налево путем чередования знаков. Видим, что наш интервал отрицательных чисел – от точки ( 2 − √ 3 ) до точки ( 2 + √ 3 ) . 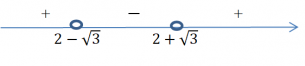Ответ: ( 2 − √ 3 ; 2 + √ 3 )

pазбирался: Даниил Романович | обсудить разбор | оценить

Решение неравенств второй степени с одной переменной. 9-й класс

Класс: 9

Презентация к уроку

Тип урока: Изучение нового материала.

1. Научить решать неравенства второй степени с одной переменной.
2. Развивать логическое мышление, математическую речь, познавательный интерес к предмету.
3. Воспитывать прилежание, трудолюбие, аккуратность, точность.

1. Актуализация знаний.
2. Постановка цели.
3. Изучение нового материала.
4. Закрепление изученного материала.
5. Обучающая самостоятельная работа.
6. Домашнее задание.
7. Подведение итогов.

1. Актуализация знаний.

– Какую функцию мы изучаем?
– Определение квадратичной функции.
– Давайте поработаем устно, чтобы хорошо усвоить новый материал.

1. Определить количество корней уравнения ах 2 + вх + с = 0 и знак коэффициента а, если график квадратной функции у = ах 2 + вх + с расположен следующим образом:

2. Укажите промежутки, в которых функция у=ах 2 +вх+с принимает положительные и отрицательные значения, если её график расположен указанным образом:

2. Постановка цели.

– Мы с вами умеем строить график квадратичной функции, умеем решать квадратные уравнения, а сегодня мы должны научиться решать неравенства второй степени с одной переменной.

Запишем тему урока в тетрадь.

3. Изучение нового материала.

• Итак, какой формулой задаётся квадратичная функция?
• Какой вид имеет квадратное уравнение?
• Какой вид имеет квадратный трёхчлен?
• Как вы думаете, какой вид будет иметь неравенство второй степени с одной переменной? ах 2 + вх + с > 0 и ах 2 + вх + с 2 + вх + с > 0 и ах 2 + вх + с 2 + 9х – 2 > 0.

– Какая квадратичная функция соответствует данному неравенству:

– Что является её графиком?
– Выясним, как расположена парабола относительно оси х.
– Как она может быть расположена (пересекать ось х, находиться выше оси х, ниже оси х, касаться оси х)?
– Как это определить?

2. Нули функции, у = 0.

3. Покажем схематически, как расположена парабола в координатной плоскости.

Запишем алгоритм решения неравенств второй степени с одной переменной.

1. Рассмотреть функцию, соответствующую данному неравенству, определить направление ветвей параболы.
2. Найти нули функции, т.е. абсциссы точек пересечения параболы с осью х, если они есть.
3. Изобразить схематически параболу в координатной плоскости.
4. Выбрать нужные промежутки.
5. Записать ответ.

Рассмотрим пример 3 и пример 4 в учебнике на странице 43. Сделаем соответствующие выводы.

4. Закрепление изученного материала.

Выполняем № 114 (а, в, д).

5. Обучающая самостоятельная работа.

Предлагается решить 3 неравенства, затем на доске показываются правильные ответы, для того, чтобы учащиеся могли проверить свои решения. Во время решения учащиеся консультируются с учителем. Те, кто успешно справится с решением, получат оценки.

Поднятием рук проверяем, как учащиеся усвоили новый материал.

6. Домашнее задание.

п.8, № 114(б, г, е), № 117 (предварительно нужно составить неравенство, а затем его решить).

7. Подведение итогов.

– Какова была цель нашего урока?
– Сформулируйте определение неравенств второй степени с одной переменной.
– Как решать такие неравенства?
– Алгоритм решения.

Тема урока: Решение неравенств второй степени с одной переменной.
Тип урока: Изучение нового материала.
Цели урока:

1. Научить решать неравенства второй степени с одной переменной.
2. Развивать логическое мышление, математическую речь, познавательный интерес к предмету.
3. Воспитывать прилежание, трудолюбие, аккуратность, точность.

1. Данный урок – урок изучения нового материала, первый урок по данной теме, всего три урока, второй и третий уроки – закрепление изученного материала и проверка усвоения материала.

2. Тема, над которой я работаю “Развитие познавательного интереса на уроках математики с целью повышения мотивации обучения”, на данном уроке я реализовала свою методическую работу посредством:
– актуализации знаний учащихся;
– создания проблемной ситуации;
– самопроверки;
– самостоятельного формулирования определения.

3. Были учтены особенности данного класса, в соответствии, с чем был построен ход урока, подобраны задания для обучающей самостоятельной работы, уровень сложности и самопроверка своих решений.

4. Ход урока логически продуман: теория → практика → самопроверка → частичное самооценивание.

5. Использовались следующие методы обучения:
– словесный;
– наглядный;
– практический.

Различные виды деятельности:
– устная работа;
– фронтальная работа;
– письменная работа;
– работа с учебником;
– работа в тетрадях;
– самостоятельная работа;
– самопроверка;
– комментирование.

6. Отклонений от хода урока не было, что запланировано – все сделали, урок своей цели достиг за счет эффективного использования методов и средств обучения, приемов контроля и самоконтроля, рационального распределения времени. Самостоятельная работа показала, что почти все учащиеся усвоили новый материал.

На третьем уроке была проведена проверочная работа, где учащиеся показали следующие результаты: