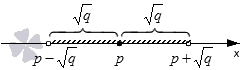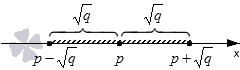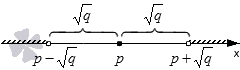Как решать уравнения методом выделения квадрата

Как решать уравнения методом выделения квадрата

Описание метода выделения полного квадрата

§2. Выделение полного квадрата из квадратного трёхчлена

Описание метода выделения полного квадрата

Выражения вида 2 x 2 + 3 x + 5 , `-4x^2+5x+7` носят название квадратного трёхчлена. В общем случае квадратным трёхчленом называют выражение вида a x 2 + b x + c , где a , b , c a, b, c – произвольные числа, причём a ≠ 0 .

Рассмотрим квадратный трёхчлен x 2 — 4 x + 5 . Запишем его в таком виде: x 2 — 2 · 2 · x + 5 . Прибавим к этому выражению 2 2 и вычтем 2 2 , получаем: x 2 — 2 · 2 · x + 2 2 — 2 2 + 5 . Заметим, что x 2 — 2 · 2 · x + 2 2 = ( x — 2 ) 2 , поэтому

x 2 — 4 x + 5 = ( x — 2 ) 2 — 4 + 5 = ( x — 2 ) 2 + 1 .

Преобразование, которое мы сделали, носит название «выделение полного квадрата из квадратного трёхчлена».

Выделите полный квадрат из квадратного трёхчлена 9 x 2 + 3 x + 1 .

Заметим, что 9 x 2 = ( 3 x ) 2 , `3x=2*1/2*3x`. Тогда

Прибавим и вычтем к полученному выражению `(1/2)^2`, получаем

Покажем, как применяется метод выделения полного квадрата из квадратного трёхчлена для разложения квадратного трёхчлена на множители.

Разложите на множители квадратный трёхчлен 4 x 2 — 12 x + 5 .

Выделяем полный квадрат из квадратного трёхчлена:

2 x 2 — 2 · 2 x · 3 + 3 2 — 3 2 + 5 = 2 x — 3 2 — 4 = ( 2 x — 3 ) 2 — 2 2 .

Теперь применяем формулу a 2 — b 2 = ( a — b ) ( a + b ) , получаем:

( 2 x — 3 — 2 ) ( 2 x — 3 + 2 ) = ( 2 x — 5 ) ( 2 x — 1 ) .

Разложите на множители квадратный трёхчлен — 9 x 2 + 12 x + 5 .

— 9 x 2 + 12 x + 5 = — 9 x 2 — 12 x + 5 . Теперь замечаем, что 9 x 2 = 3 x 2 , — 12 x = — 2 · 3 x · 2 .

Прибавляем к выражению 9 x 2 — 12 x слагаемое 2 2 , получаем:

— 3 x 2 — 2 · 3 x · 2 + 2 2 — 2 2 + 5 = — 3 x — 2 2 — 4 + 5 = — 3 x — 2 2 + 4 + 5 = = — 3 x — 2 2 + 9 = 3 2 — 3 x — 2 2 .

Применяем формулу для разности квадратов, имеем:

— 9 x 2 + 12 x + 5 = 3 — 3 x — 2 3 + ( 3 x — 2 ) = ( 5 — 3 x ) ( 3 x + 1 ) .

Разложите на множители квадратный трёхчлен 3 x 2 — 14 x — 5 .

Мы не можем представить выражение 3 x 2 как квадрат какого-то выражения, т. к. ещё не изучали этого в школе. Это будете проходить позже, и уже в Задании №4 будем изучать квадратные корни. Покажем, как можно разложить на множители заданный квадратный трёхчлен:

Покажем, как применяется метод выделения полного квадрата для нахождения наибольшего или наименьшего значений квадратного трёхчлена.
Рассмотрим квадратный трёхчлен x 2 — x + 3 . Выделяем полный квадрат:

`(x)^2-2*x*1/2+(1/2)^2-(1/2)^2+3=(x-1/2)^2+11/4`. Заметим, что при `x=1/2` значение квадратного трёхчлена равно `11/4`, а при `x!=1/2` к значению `11/4` добавляется положительное число, поэтому получаем число, большее `11/4`. Таким образом, наименьшее значение квадратного трёхчлена равно `11/4` и оно получается при `x=1/2`.

Найдите наибольшее значение квадратного трёхчлена — 16 x 2 + 8 x + 6 .

Выделяем полный квадрат из квадратного трёхчлена: — 16 x 2 + 8 x + 6 = — 4 x 2 — 2 · 4 x · 1 + 1 — 1 + 6 = — 4 x — 1 2 — 1 + 6 = = — 4 x — 1 2 + 7 .

При `x=1/4` значение квадратного трёхчлена равно 7 , а при `x!=1/4` из числа 7 вычитается положительное число, то есть получаем число, меньшее 7 . Таким образом, число 7 является наибольшим значением квадратного трёхчлена, и оно получается при `x=1/4`.

Разложите на множители числитель и знаменатель дроби `/` и сократите эту дробь.

Заметим, что знаменатель дроби x 2 — 6 x + 9 = x — 3 2 . Разложим числитель дроби на множители, применяя метод выделения полного квадрата из квадратного трёхчлена.

x 2 + 2 x — 15 = x 2 + 2 · x · 1 + 1 — 1 — 15 = x + 1 2 — 16 = x + 1 2 — 4 2 = = ( x + 1 + 4 ) ( x + 1 — 4 ) = ( x + 5 ) ( x — 3 ) .

Данную дробь привели к виду `<(x+5)(x-3)>/(x-3)^2` после сокращения на ( x — 3 ) получаем `(x+5)/(x-3)`.

Разложите многочлен x 4 — 13 x 2 + 36 на множители.

Применим к этому многочлену метод выделения полного квадрата.

Разложите на множители многочлен 4 x 2 + 4 x y — 3 y 2 .

Применяем метод выделения полного квадрата. Имеем:

( 2 x ) 2 + 2 · 2 x · y + y 2 — y 2 — 3 y 2 = ( 2 x + y ) 2 — 2 y 2 = = ( 2 x + y + 2 y ) ( 2 x + y — 2 y ) = ( 2 x + 3 y ) ( 2 x — y ) .

Применяя метод выделения полного квадрата, разложите на множители числитель и знаменатель и сократите дробь `<8x^2+10x-3>/<2x^2-x-6>`.

Решение квадратных неравенств через выделение квадрата двучлена

Квадратные неравенства можно решать несколькими разными способами. Для лучшего понимания сути этих выражений полезно знать их все. Помимо привычного метода интервалов или графического способа существует и метод решения через выделение квадрата двучлена, о котором мы вам расскажем в данном материале.

Выделив квадрат двучлена в левой части, можно легко решить практически любое квадратное неравенство. Сейчас мы разберем данный метод по порядку, иллюстрируя каждый шаг решениями задач.

Основа метода выделения квадрата двучлена

Для начала объясним основную суть данного подхода на примере условного квадратного неравенства a · x 2 + b · x + c 0 . Между выражениями при этом может стоять и знак ≤ , и ≥ , и > , это не принципиальный момент. Суть метода заключается в переходе от исходного неравенства к равносильному, которое имеет вид ( x − p ) 2 q ( ≤ , > , ≥ ) , при этом p и q могут быть произвольными числами. Для этого мы используем равносильные преобразования, подробно описанные в одной из предыдущих статей. По полученному равенству можно будет судить о решении исходного.

Теперь перейдем к объяснению следующих двух моментов: как именно привести заданное в условии равенство к нужному виду и как потом его нужно решать.

Как преобразовать исходное равенство в (x−p) 2 , ≥)

Для этого нам нужно последовательно выполнить несколько шагов. Вот они:

1. Если мы имеем коэффициент a , который не равен 1 , то нам нужно разделить на него правую и левую часть равенства. Если он меньше 0 , то знак неравенства остается прежним, а если больше, то нужно поменять его на противоположный. В итоге у нас должно получиться равенство с коэффициентом при x 2 , которое будет равносильно исходному. Если коэффициент при x 2 равен единице, то первый шаг нужно пропустить.
2. Далее смотрим на коэффициент при x . Если он не равен нулю, то мы можем слева выделить нужный нам квадрат двучлена. Если же слагаемое с x в первой степени у нас отсутствует совсем, то этот шаг мы тоже пропускаем.
3. После этих действий нужно перенести оставшееся слагаемое-число направо с противоположным знаком.

Мы получили неравенство нужного нам вида. Разберем решения конкретных задач, чтобы увидеть преобразования на практике.

Допустим, у нас есть неравенство x 2 ≥ 0 . Видим, что коэффициент при x 2 – единица, значит, первый и второй шаги можно пропустить. Получается, что и на третьем шаге ничего не нужно переносить, ведь слагаемого-числа с левой стороны нет. Из этого заключаем, что имеющееся у нас неравенство уже имеет нужный нам вид ( x − p ) 2 ≥ q , только p = 0 и q = 0 .

Ответ: имеющееся у нас неравенство уже имеет нужный нам вид ( x − p ) 2 ≥ q

Возьмем пример чуть сложнее.

Так, у нас есть квадратное неравенство 5 · x 2 0 . Выполняем первый шаг, разделив обе части на старший коэффициент, равный пяти. Поскольку 5 больше нуля, знак равенства при этом не меняется. После этого неравенство приобретает вид x 2 0 , что соответствует нужным условиям при p = 0 и q = 0 . Два следующих шага можно пропустить.

Ответ: x 2 0

Если у нас есть квадратное неравенство — 3 · x 2 — 4 > 0 , то сначала мы должны выполнить деление обоих частей на — 3 . Поскольку делитель является отрицательным числом, то нужно будет поменять знак равенства на противоположный. У нас получится x 2 + 4 3 0 . Избавившись от иррациональности в знаменателе, запишем x 2 + 4 3 0 . Коэффициента при x у нас нет, поэтому второй шаг пропускаем. На последнем этапе переносим оставшийся свободный член вправо и получаем x 2 — 4 3 3 . Полученное равенство соответствует нужному нам виду ( x − p ) 2 q , причем p = 0 , и q = — 4 3 3 .

Ответ: x 2 — 4 3 3

Разберем преобразование неравенства 1 3 x 2 + 2 · x + 3 ≤ 0 . Первым делом разделим обе части на одну треть. Это действие аналогично умножению на три. Сохранив знак неравенства, получим x 2 + 6 · x + 9 ≤ 0 . Поскольку слагаемое с x у нас есть, нам нужно выделить квадрат двучлена: ( x + 3 ) 2 ≤ 0 . Последний шаг мы не выполняем, поскольку числового слагаемого не осталось. Таким образом, мы заменили исходное квадратное неравенство на равносильное ему ( x − p ) 2 ≤ q , где p = − 3 и q = 0 .

Ответ: ( x + 3 ) 2 ≤ 0

Посмотрим еще один пример с квадратным неравенством 4 · x 2 − 4 · x − 1 0 . Начнем с деления на коэффициент при x 2 , т.е. на четыре. У нас получится x 2 — x — 1 4 0 . Выделяем квадрат двучлена: x 2 — 2 · 1 2 · x + 1 2 2 — 1 2 2 — 1 4 0 и далее x — 1 2 2 — 1 2 0 . Осталось перенести оставшееся свободное слагаемое в правую часть с другим знаком. Итоговое равносильное неравенство имеет вид x — 1 2 2 1 2 , где p = 1 2 , q = 1 2 .

Ответ: x — 1 2 2 1 2

Решение полученного неравенства (x−p) 2 , ≥)

Мы разобрали, как правильно преобразовывать имеющиеся неравенства для приведения их к исходному виду. Далее рассмотрим, как найти их решение. Разберем три основных случая, когда q больше 0 , меньше 0 или равно 0 .

Решение при q, меньшем 0

В этом случае в основе решения лежит свойство степени: любое число, возведенное в квадрат, является неотрицательным. Мы помним также, что квадрат числа, не равного нулю, всегда положителен, а квадрат нуля равен 0 только в том случае, если 0 лежит в основании степени. В буквенном виде это можно записать как d 2 ≥ 0 для любого d , d 2 > 0 при любом d ≠ 0 , и d 2 = 0 только тогда, когда d = 0 .

Допустим, что в основании лежит отрицательное число. Значение ( x − p ) 2 , согласно указанным выше свойствам квадрата, не может быть отрицательным. Следовательно, будут справедливы неравенства ( x − p ) 2 p и ( x − p ) 2 ≤ p , причем x может быть любым. Таким образом, любое действительное число может считаться решением этих неравенств.

А вот ( x − p ) 2 p и ( x − p ) 2 ≤ p не будут справедливыми ни при каких значениях x . Из этого можно сделать вывод, что решений у них нет.

Условие: найдите решение квадратного неравенства x 2 + 4 · x + 5 > 0 .

Решение

Cначала нам нужно выделить полный квадрат с левой стороны.

x 2 + 2 · 2 · x + 2 2 − 2 2 + 5 > 0 , ( x + 2 ) 2 + 1 > 0

После этого переносим 1 вправо: ( x + 2 ) 2 > − 1 .

У нас получилось равенство, равносильное исходному. Для него любое действительное число может стать решением, поскольку выражение слева будет неотрицательным всегда, при любом значении x . То же можно сказать и о ( x + 2 ) 2 > − 1 . Значит, решением неравенства, заданного в условии, может быть любое действительное число.

Ответ: любое действительное число.

Условие: вычислите 9 · x 2 + 6 · x + 28 ≤ 0 .

Решение

Для данного квадратного неравенства подходит метод решения с помощью выделения квадрата двучлена. Для начала разделим левую и правую часть неравенства на девять и выделим нужный квадрат. У нас осталось одно слагаемое, которое надо перенести в правую часть с противоположным знаком.

x 2 + 2 3 · x + 28 9 ≤ 0 x 2 + 2 · 1 3 · x + 1 3 2 — 1 3 2 + 28 9 ≤ 0 x + 1 3 2 + 3 ≤ 0 x + 1 3 2 ≤ — 3

Выражение в левой части будет неотрицательным при любом значении x . Это значение также не может быть равно — 3 или быть меньше него. Получается, что итоговое равенство не имеет решения, следовательно, и исходное равенство, которое равносильно ему, также решений иметь не будет.

Ответ: решений у данного неравенства нет.

Решение при q, равном 0

Допустим, что значение q равно 0 , тогда нам нужно рассмотреть неравенства ( x − p ) 2 0 , ( x − p ) 2 ≤ 0 , ( x − p ) 2 > 0 и ( x − p ) 2 ≥ 0 ) . Зная свойства числа, возведенного в квадрат, мы можем заключить, что значение ( x − p ) 2 будет больше нуля при таких значениях x , которые будут соответствовать условию x − p ≠ 0 , и будет равно нулю, если x − p = 0 .

1. ( x − p ) 2 > 0 будет верным неравенством при таких значениях переменной x , когда x − p ≠ 0 , то есть при x ≠ p .
2. ( x − p ) 2 ≥ 0 не будет верным равенством ни при одном действительном x , если x − p = 0 .

Условие: выясните, есть ли решения у квадратного неравенства − 0 , 2 · x 2 + 4 · x − 20 ≥ 0 .

Решение

Начнем с необходимых равносильных преобразований.

x 2 − 20 · x + 100 ≤ 0 ( x − 10 ) 2 ≤ 0 .

Получившееся в итоге равенство будет справедливым лишь в том случае, если x − 10 = 0 . Получается, что нужное нам значение x равно 10 . Следовательно, это число и будет единственным решением исходного неравенства.

Ответ: есть единственное решение 10 .

Условие: найти решение 16 · x 2 + 40 · x + 25 > 0 .

Решение

Начнем с деления на 16 , после чего нужно выделить квадрат двучлена.

x 2 + 5 2 · x + 25 16 > 0 x + 5 4 2 > 0 x + 1 1 4 > 0

Это неравенство имеет решения. Оно будет верным для всех значений x , за исключением такого, которое обратит основание степени в 0 , т.е. x ≠ — 1 1 4 .

Ответ: — ∞ , — 1 1 4 ∪ — 1 1 4 , + ∞

Решение при q, большем 0

Последний случай, который нам нужно разобрать, – это решение неравенств ( x − p ) 2 q , ( x − p ) 2 ≤ q , ( x − p ) 2 > q и ( x − p ) 2 ≥ q при значении q больше 0 .

Для этого нам понадобится вспомнить другие свойства корня: неравенство u v ( ≤ , > , ≥ ) можно преобразовать в u v при любых положительных u и v ; для любого положительного t является верным равенство t 2 = t .

Первое свойство позволяет нам перейти от обычного квадратного неравенства к иррациональному, а второе ­– к неравенству с модулем. В обоих случаях полученные неравенства будут равносильными исходному.

Чтобы решить неравенство с модулем, нужно раскрыть этот модуль. Так, мы можем преобразовать x — p q в две системы неравенств без модуля x — p ≥ 0 x — p q и x — p 0 — x — p q . Покажем пример решения задачи.

Условие: вычислите x 2 − 6 · x − 7 > 0 , предварительно выделив квадрат двучлена.

Решение

Выделив нужный квадрат, получим x 2 − 2 · 3 · x + 3 2 − 3 2 − 7 > 0 , ( x − 3 ) 2 − 16 > 0 . Теперь перенесем слагаемое — 16 вправо с положительным знаком и получим ( x − 3 ) 2 > 16 . Теперь запишем равносильное ему иррациональное неравенство x — 3 2 > 16 ,далее | x − 3 | > 4 . Теперь преобразуем его в совокупность двух систем неравенств, чтобы избавиться от модуля.

x — 3 ≥ 0 x — 3 > 4 x — 3 0 — ( x — 3 ) > 4 x ≥ 3 x > 7 x 3 x — 1 x > 7 x — 1

У нас получилось, что решением исходного квадратного неравенства будет x − 1 , x > 7 .

Ответ: x − 1 , x > 7 .

Существует еще один удобный и наглядный способ решения неравенств x — p q ( ≤ , > , ≥ ) . С его помощью можно обойтись без введения систем. Для его применения необходимо понимать геометрический смысл модуля.

В рамках геометрических представлений модуль | x − p | представляет собой расстояние то точки с координатой x до точки с координатой p , отложенное по оси координат. Отсюда можно сделать следующие выводы:

1. Решениями неравенства x — p q будут координаты таких точек, расстояние от которых до точки с координатой p будет меньшим, чем значение q . См. на иллюстрацию:

Таким образом, данному неравенству будут удовлетворять значения переменных из интервала p — q , p + q .

1. Решением неравенства x — p ≤ q будут все те значения x , при которых расстояние от точки с координатой p будет меньше или равно q . Графически это можно представить так:

Следовательно, решением данного неравенства будут числа из интервала p — q , p + q

1. Если нам нужно найти решение x — p > q , то мы должны взять точки, расстояние от которых до точки p будет больше q . См. на иллюстрацию:

Решения данного неравенства будут лежат в интервале — ∞ , p — q ∪ p + q , + ∞ .

Вернемся к решению предыдущей задачи, чтобы наглядно показать эти выкладки.

Условие: найдите решения квадратного неравенства x 2 − 6 · x − 7 > 0 .

Решение: выполним все необходимые равносильные преобразования, выделив квадрат двучлена слева, и приведем исходное неравенство к нужному нам виду ( x − 3 ) 2 > 16 . Далее запишем:

( x — 3 ) 2 > 16 x — 3 > 4

Полученному неравенству будут удовлетворять координаты всех точек, расположенных от точки с координатой 3 на расстоянии больше 4 . Покажем на рисунке:

Разложение многочленов на множители. Метод выделения полного квадрата. Комбинация методов

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы вспомним все ранее изученные методы разложения многочлена на множители и рассмотрим примеры их применения, кроме того, изучим новый метод — метод выделения полного квадрата и научимся применять его при решении различных задач.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»