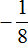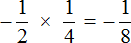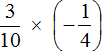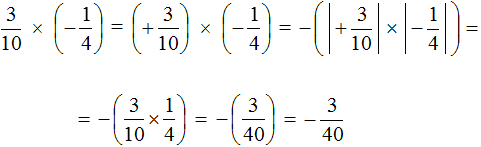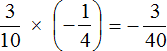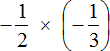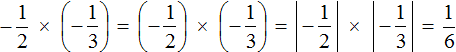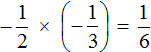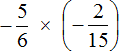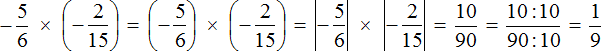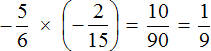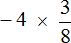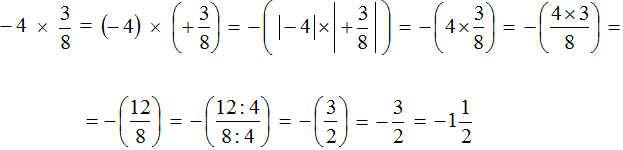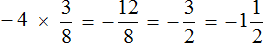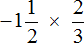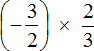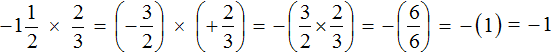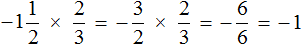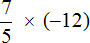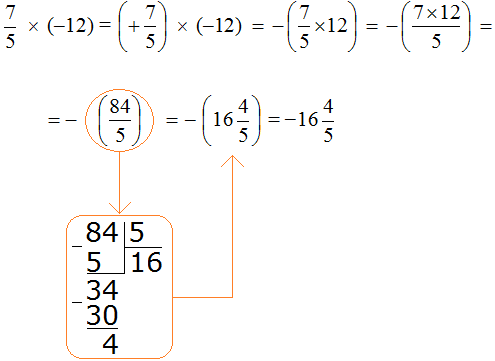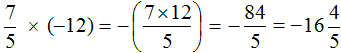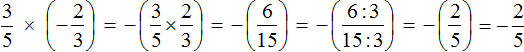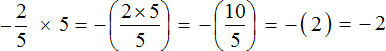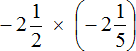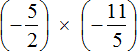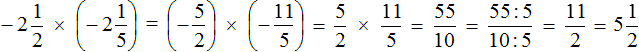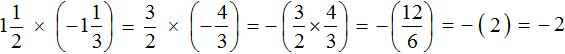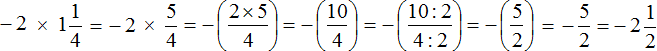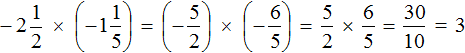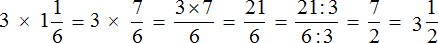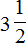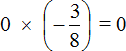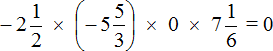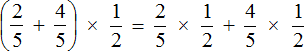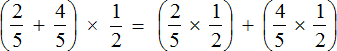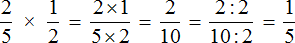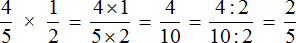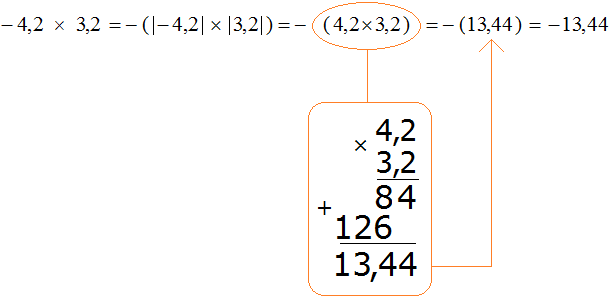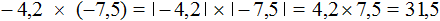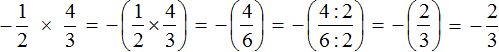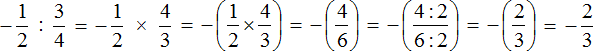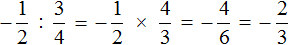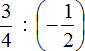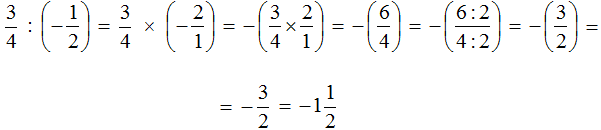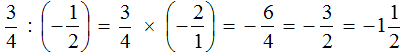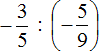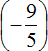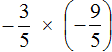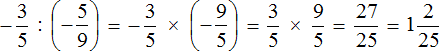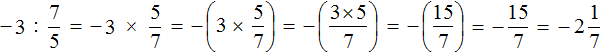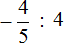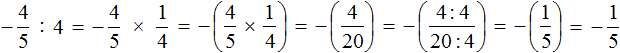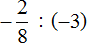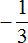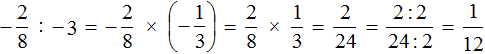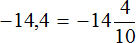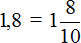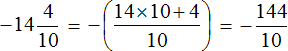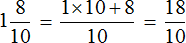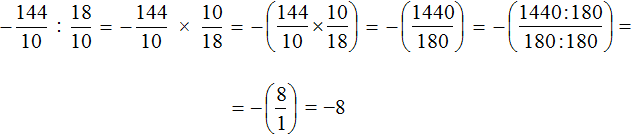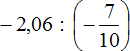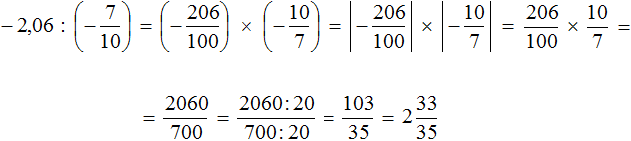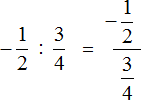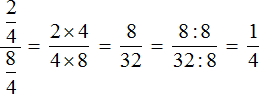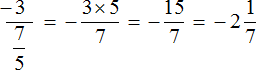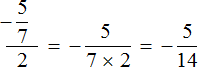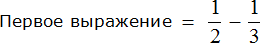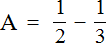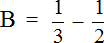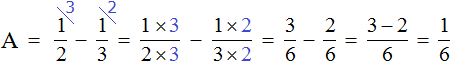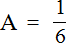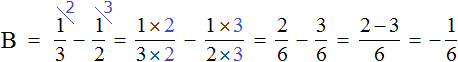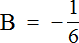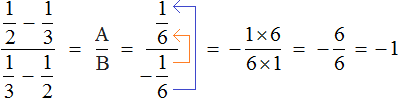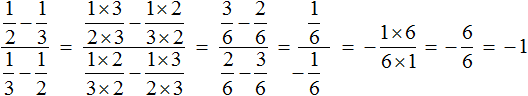Как решать уравнения на деления рациональных чисел

Решение уравнений с дробями

О чем эта статья:

5 класс, 6 класс, 7 класс

Понятие дроби

Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.

Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:

• обыкновенный вид — ½ или a/b,
• десятичный вид — 0,5.

Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.

Дроби бывают двух видов:

1. Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
2. Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.

Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.

Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.

Основные свойства дробей

Дробь не имеет значения, если делитель равен нулю.

Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.

Дроби a/b и c/d называют равными, если a × d = b × c.

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.

Понятие уравнения

Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:

• Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
• Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.

Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.

Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.

Решить уравнение значит найти все его корни или убедиться, что корней нет.

Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.

Понятие дробного уравнения

Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:

Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.

Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:

На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.

Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.

Как решать уравнения с дробями

1. Метод пропорции

Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.

Итак, у нас есть линейное уравнение с дробями:

В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.

После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.

2. Метод избавления от дробей

Возьмем то же самое уравнение, но попробуем решить его по-другому.

В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:

• подобрать число, которое можно разделить на каждый из знаменателей без остатка;
• умножить на это число каждый член уравнения.

Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!

Вот так просто мы получили тот же ответ, что и в прошлый раз.

Что еще важно учитывать при решении

• если значение переменной обращает знаменатель в 0, значит это неверное значение;
• делить и умножать уравнение на 0 нельзя.

Универсальный алгоритм решения

Определить область допустимых значений.

Найти общий знаменатель.

Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.

Раскрыть скобки, если нужно и привести подобные слагаемые.

Решить полученное уравнение.

Сравнить полученные корни с областью допустимых значений.

Записать ответ, который прошел проверку.

Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.

Примеры решения дробных уравнений

Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.

Пример 1. Решить дробное уравнение: 1/x + 2 = 5.

1. Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
2. Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Решим обычное уравнение.

Пример 2. Найти корень уравнения

1. Область допустимых значений: х ≠ −2.
2. Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
3. Избавимся от знаменателя. Умножим каждый член уравнения на х.

Переведем новый множитель в числитель..

Сократим левую часть на (х+2), а правую на 2.

Пример 3. Решить дробное уравнение:

Найти общий знаменатель:

Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:

Выполним возможные преобразования. Получилось квадратное уравнение:

Решим полученное квадратное уравнение:

Получили два возможных корня:

Если x = −3, то знаменатель равен нулю:

Если x = 3 — знаменатель тоже равен нулю.

Умножение и деление рациональных чисел

В данном уроке рассматривается умножение и деление рациональных чисел.

Умножение рациональных чисел

Правила умножения целых чисел справедливы и для рациональных чисел. Иными словами, чтобы умножать рациональные числа, нужно уметь умножать целые числа.

Необходимо также знать основные законы умножения такие как переместительный закон умножения, сочетательный закон умножения, распределительный закон умножения и закон умножения на ноль.

Пример 1. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Чтобы перемножить рациональные числа с разными знаками, нужно перемножить их модули и перед полученным ответом поставить минус.

Чтобы хорошо увидеть, что мы имеем дело с числами, у которых разные знаки, заключим каждое рациональное число в скобки вместе со своими знаками

Модуль числа равен , а модуль числа равен . Перемножив полученные модули, как положительные дроби, мы получили ответ , но перед ответом поставили минус, как от нас требовало правило. Чтобы обеспечить перед ответом этот минус, умножение модулей выполнялось в скобках, перед которыми и поставлен минус.

Таким образом, значение выражения 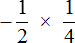равно

Короткое решение выглядит следующим образом:

Пример 2. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус:

Решение для данного примера можно записать покороче:

Пример 3. Найти значение выражения

Это умножение отрицательных рациональных чисел. Чтобы перемножить отрицательные рациональные числа, нужно перемножить их модули и перед полученным ответом поставить плюс

Решение для данного примера можно записать покороче:

Пример 4. Найти значение выражения

Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс

Решение для данного примера можно записать покороче:

Пример 5. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

Короткое решение будет выглядеть значительно проще:

Пример 6. Найти значение выражения

Переведём смешанное число 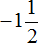в неправильную дробь. Остальное перепишем, как есть

Получили умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус. Запись с модулями можно пропустить, чтобы не загромождать выражение

Решение для данного примера можно записать покороче

Пример 7. Найти значение выражения

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

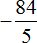
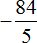
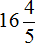
Сначала в ответе получилась неправильная дробь , но мы выделили в ней цéлую часть. Обратите внимание, что целая часть была выделена от модуля дроби . Получившееся смешанное число было заключено в скобки, перед которыми поставлен минус. Это сделано для того, чтобы выполнялось требование правила. А правило требовало, чтобы перед полученным ответом стоял минус.

Решение для данного примера можно записать покороче:

Пример 8. Найти значение выражения

Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.

Сначала перемножим и и полученное число перемножим с оставшимся числом 5. Запись с модулями пропустим, чтобы не загромождать выражение.

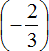
Первое действие:

Второе действие:

Ответ: значение выражения 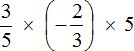равно −2.

Пример 9. Найти значение выражения:

Переведём смешанные числа в неправильные дроби:

Получили умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс. Запись с модулями можно пропустить, чтобы не загромождать выражение

Пример 10. Найти значение выражения

Выражение состоит из нескольких сомножителей. Согласно сочетательному закону умножения, если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий. Это позволяет нам вычислить данное выражение в любом порядке.

Не будем изобретать велосипед, а вычислим данное выражение слева направо в порядке следования сомножителей. Запись с модулями пропустим, чтобы не загромождать выражение

Первое действие:

Второе действие:

Третье действие:

Четвёртое действие:

Ответ: значение выражения 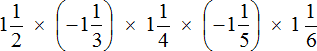равно

Пример 11. Найти значение выражения

Вспоминаем закон умножения на ноль. Этот закон гласит, что произведение равно нулю, если хотя бы один из сомножителей равен нулю.

В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения 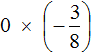равно нулю:

Пример 12. Найти значение выражения

Произведение равно нулю, если хотя бы один из сомножителей равен нулю.

В нашем примере один из сомножителей равен нулю, поэтому не теряя времени отвечаем, что значение выражения 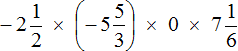равно нулю:

Пример 13. Найти значение выражения

Можно воспользоваться порядком действий и сначала вычислить выражение в скобках 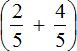и полученный ответ перемножить с дробью .

Ещё можно воспользоваться распределительным законом умножения — умножить каждое слагаемое суммы 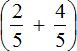на дробь и полученные результаты сложить. Этим способом и воспользуемся.

Согласно порядку действий, если в выражении присутствует сложение и умножение, то в первую очередь нужно выполнять умножение. Поэтому в получившемся новом выражении возьмём в скобки те дроби, которые должны быть перемножены. Так мы хорошо увидим, какие действия выполнить раньше, а какие позже:

Далее вычисляем выражение по действиям. Сначала вычислим выражения в скобках, и полученные результаты сложим

Первое действие:

Второе действие:

Третье действие:

Ответ: значение выражения 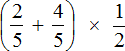равно

Решение для данного примера можно записать значительно короче. Выглядеть оно будет следующим образом:

Видно, что данный пример можно было решить даже в уме. Поэтому следует развивать в себе навык анализа выражения до начала его решения. Вполне вероятно, что его можно решить в уме и сэкономить много времени и нервов. А на контрольных и экзаменах, как известно время очень дорого стоит.

Пример 14. Найти значение выражения −4,2 × 3,2

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичные дроби.

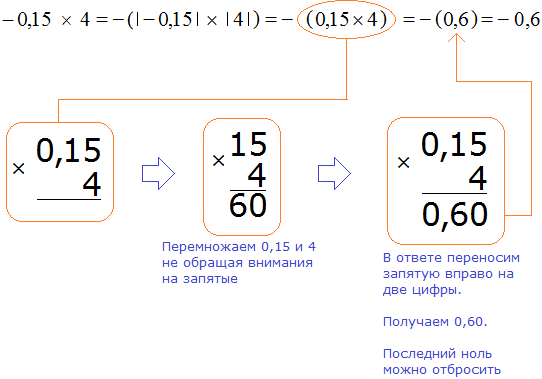
Пример 15. Найти значение выражения −0,15 × 4

Это умножение рациональных чисел с разными знаками. Перемножим модули этих чисел и перед полученным ответом поставим минус

Обратите внимание, как перемножались модули рациональных чисел. В данном случае, чтобы перемножить модули рациональных чисел, потребовалось суметь перемножить десятичную дробь и целое число.

Пример 16. Найти значение выражения −4,2 × (−7,5)

Это умножение отрицательных рациональных чисел. Перемножим модули этих чисел и перед полученным ответом поставим плюс

Деление рациональных чисел

Деление рациональных чисел свóдится к умножению этих же чисел. Для этого первую дробь умножают на дробь, обратную второй. Затем применяются правила умножения рациональных чисел.

Пример 1. Выполнить деление:

Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь . На неё и умножим первую дробь:

Получили умножение рациональных чисел с разными знаками. А как вычислять такие выражения мы уже знаем. Для этого нужно перемножить модули данных рациональных чисел и перед полученным ответом поставить минус.

Дорешаем данный пример до конца. Запись с модулями можно пропустить, чтобы не загромождать выражение

Таким образом, значение выражения 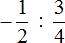равно

Подробное решение выглядит следующим образом:

Короткое решение можно записать так:

Пример 2. Выполнить деление

Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь 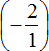. На неё и умножим первую дробь:

Короткое решение можно записать так:

Пример 3. Выполнить деление

Умнóжим первую дробь на дробь, обратную второй. Обратная для второй дроби это дробь

Получили умножение отрицательных рациональных чисел. Выполним данное умножение. Запись с модулями можно пропустить, чтобы не загромождать выражение:

Пример 4. Выполнить деление

В данном случае нужно первое число −3 умножить на дробь, обратную дроби .

Обратная для дроби это дробь . Затем следует применить правило умножения рациональных чисел с разными знаками:

Пример 6. Выполнить деление

Умнóжим первую дробь на число, обратное числу 4 .

Обратное числу 4 это дробь . На неё и умножим первую дробь

Пример 5. Выполнить деление

Умнóжим первую дробь на число, обратное числу −3

Обратное числу −3 это дробь

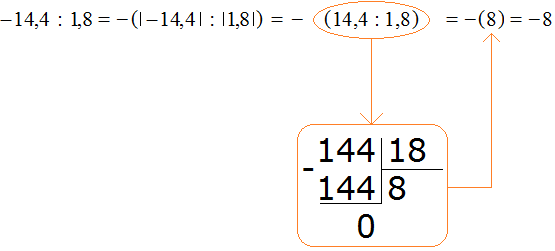
Пример 6. Найти значение выражение −14,4 : 1,8

Это деление рациональных чисел с разными знаками. Чтобы вычислить данное выражение, нужно модуль делимого разделить на модуль делителя и перед полученным ответом поставить минус

Обратите внимание, как модуль делимого был разделён на модуль делителя. В данном случае потребовалось суметь разделить десятичную дробь на другую десятичную дробь.

Если нет желания работать с десятичными дробями (а это бывает часто), то эти десятичные дроби можно перевести в смешанные числа, затем перевести эти смешанные числа в неправильные дроби, а затем заняться непосредственно делением.

Вычислим предыдущее выражение −14,4 : 1,8 этим способом. Переведём десятичные дроби в смешанные числа:

Теперь переведём полученные смешанные числа в неправильные дроби:

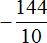
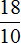
Теперь можно заняться непосредственно делением, а именно разделить дробь на дробь . Для этого нужно первую дробь умножить на дробь, обратную второй:

Пример 7. Найти значение выражения

Переведём десятичную дробь −2,06 в неправильную дробь, и умножим эту дробь на дробь, обратную второй:0

Пример 8. Найти значение выражения −7,2 : (−0,6)

Это деление отрицательных рациональных чисел. Чтобы выполнить данное деление, нужно первую дробь умножить на дробь обратную второй.

Перенесём в обеих дробях запятую на одну цифру вправо, получим деление −72:(−6)

Многоэтажные дроби

Часто можно встретить выражение, в котором деление дробей записано с помощью дробной черты. Например, выражение 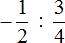может быть записано следующим образом:

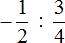
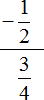
В чём же разница между выражениями и ? На самом деле разницы никакой. Эти два выражения несут одно и то же значение и между ними можно поставить знак равенства:

В первом случае знак деления представляет собой двоеточие и выражение записано в одну строку. Во втором случае деление дробей записано с помощью дробной черты. В результате получается дробь, которую в народе договорились называть многоэтажной.

При встрече с такими многоэтажными выражениями, нужно применять те же правила деления обыкновенных дробей. Первую дробь необходимо умножать на дробь, обратную второй.

Использовать в решении подобные дроби крайне неудобно, поэтому можно записать их в понятном виде, используя в качестве знака деления не дробную черту, а двоеточие.

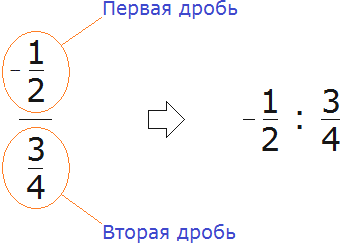
Например, запишем многоэтажную дробь 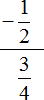в понятном виде. Для этого сначала нужно разобраться, где первая дробь и где вторая, потому что сделать это правильно удаётся не всегда. В многоэтажных дробях имеется несколько дробных черт, которые могут запутать. Главная дробная черта, которая отделяет первую дробь от второй, обычно бывает длиннее остальных.

После определения главной дробной черты можно без труда понять, где первая дробь и где вторая:

И далее можно воспользоваться методом деления дробей — умножить первую дробь на дробь, обратную второй.

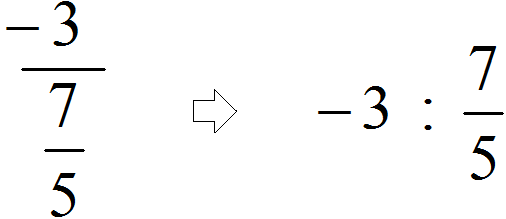
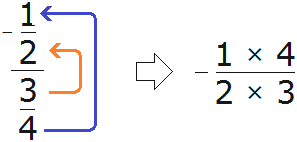
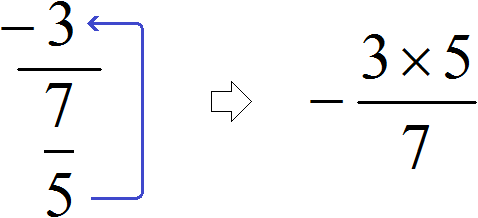
Пример 2. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление целого числа −3 на обыкновенную дробь

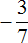
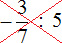
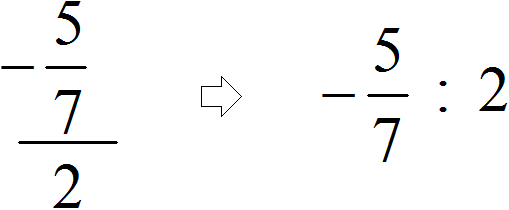
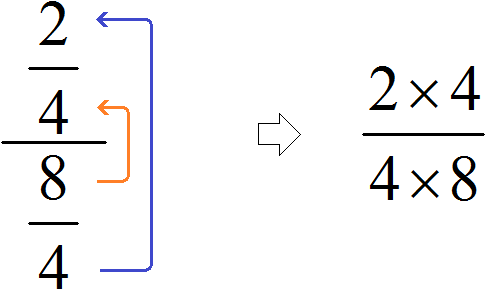
А если бы мы по ошибке приняли вторую дробную черту за главную (ту, что короче), то получилось бы, что мы делим дробь на целое число 5В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является число −3, а делителем — дробь .

Пример 3. Запишем в понятном виде многоэтажную дробь

Находим главную дробную черту (она самая длинная) и видим, что осуществляется деление дроби 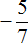на целое число 2

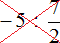
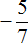
А если бы мы по ошибке приняли первую дробную черту за главную (ту, что короче), то получилось бы, что мы делим целое число −5 на дробь В этом случае, даже если это выражение вычислить верно, задача будет решена неправильно, поскольку делимым в данном случае является дробь , а делителем — целое число 2.

Несмотря на то, что многоэтажные дроби неудобны в работе, сталкиваться мы с ними будем очень часто, особенно при изучении высшей математики.

Естественно, на перевод многоэтажной дроби в понятный вид уходит дополнительное время и место. Поэтому можно воспользоваться более быстрым методом. Данный метод удобен и на выходе позволяет получить готовое выражение, в котором первая дробь уже умножена на дробь, обратную второй.

Реализуется этот метод следующим образом:

Если дробь четырехэтажная, например как 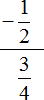, то цифру находящуюся на первом этаже поднимают на самый верхний этаж. А цифру, находящуюся на втором этаже поднимают на третий этаж. Полученные цифры нужно соединить значками умножения ( × )

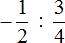
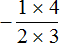
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратную второй. Удобство да и только!

Чтобы не допускать ошибок при использовании данного метода, можно руководствоваться следующим правилом:

С первого на четвёртый. Со второго на третий.

В правиле речь идет об этажах. Цифру с первого этажа нужно поднимать на четвертый этаж. А цифру со второго этажа нужно поднимать на третий этаж.

Попробуем вычислить многоэтажную дробь 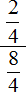пользуясь вышеприведённым правилом.

Итак, цифру находящуюся на первом этаже поднимаем на четвёртый этаж, а цифру находящуюся на втором этаже поднимаем на третий этаж

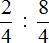
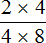
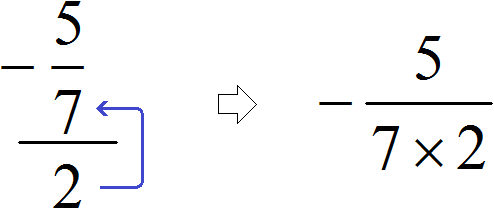
В результате, минуя промежуточную запись мы получаем новое выражение , в котором первая дробь уже умножена на дробь, обратной второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь 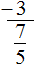пользуясь новой схемой.

Здесь имеется только первый, второй и четвёртый этажи. Третий этаж отсутствует. Но мы не отходим от основной схемы: цифру с первого этажа поднимаем на четвёртый этаж. А поскольку третий этаж отсутствует, то цифру находящуюся на втором этаже оставляем, как есть

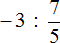
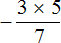
В результате, минуя промежуточную запись мы получили новое выражение , в котором первое число −3 уже умножено на дробь, обратную второй. Далее можно воспользоваться имеющимися знаниями:

Попробуем вычислить многоэтажную дробь 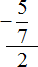, пользуясь новой схемой.

Здесь имеется только второй, третий и четвёртый этажи. Первый этаж отсутствует. Поскольку первый этаж отсутствует, подниматься на четвёртый этаж нечему, но зато мы можем поднять цифру со второго этажа на третий:

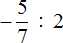
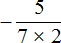
В результате, минуя промежуточную запись мы получили новое выражение , в котором первая дробь уже умножена на число, обратное делителю. Далее можно воспользоваться имеющимися знаниями:

Использование переменных

Если выражение сложное и вам кажется, что оно запутает вас в процессе решения задачи, то часть выражения можно занести в переменную и далее работать с этой переменной.

Математики часто так и делают. Сложную задачу разбивают на более лёгкие подзадачи и решают их. Затем собирают решённые подзадачи в одно единое целое. Это творческий процесс и этому учатся годами, упорно тренируясь.

Использование переменных оправдано, при работе с многоэтажными дробями. Например:

Найти значение выражения

Итак, имеется дробное выражение в числителе и в знаменателе котором дробные выражения. Другими словами, перед нами снова многоэтажная дробь, которую мы так не любим.

Выражение, находящееся в числителе 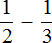можно занести в переменную с любым названием, например:

Но в математике в подобном случае переменным принято давать название из больших латинских букв. Давайте не будем нарушать эту традицию, и обозначим первое выражение через большую латинскую букву A

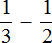
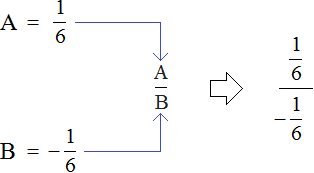
А выражение, находящееся в знаменателе можно обозначить через большую латинскую букву B

Теперь наше изначальное выражение 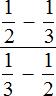принимает вид . То есть мы сделали замену числового выражения на буквенное, предварительно занеся числитель и знаменатель в переменные A и B.

Теперь мы можем отдельно вычислить значения переменной A и значение переменной B. Готовые значения мы вставим в выражение .

Найдём значение переменной A

Найдём значение переменной B

Теперь подставим в главное выражения вместо переменных A и B их значения:

Мы получили многоэтажную дробь в которой можно воспользоваться схемой «с первого на четвёртый, со второго на третий», то есть цифру находящуюся на первом этаже поднять на четвёртый этаж, а цифру находящуюся на втором этаже поднять на третий этаж. Дальнейшее вычисление не составит особого труда:

Таким образом, значение выражения 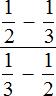равно −1.

Конечно, мы рассмотрели простейший пример, но нашей целью было узнать, как можно использовать переменные для облегчения себе задачи, чтобы свести к минимуму допущение ошибок.

Отметим также, что решение для данного примера можно записать не применяя переменные. Выглядеть оно будет как

Это решение более быстрое и короткое и в данном случае его целесообразнее так и записать, но если выражение окажется сложным, состоящим из нескольких параметров, скобок, корней и степеней, то желательно вычислять его в несколько этапов, занося часть его выражений в переменные.

Деление рациональных чисел примеры и правила.

Деление рациональных чисел в математике имеет общий смысл, ведь понятие рациональные числа включает в себя все числа, которые в них входят (натуральные числа, целые числа, десятичные числа и дробные числа). Как решать деление рациональных чисел? Деление рациональных чисел происходит по тем же правилам, что и деление всех этих чисел.

Смысл деления рациональных чисел.

Деление рациональных чисел– это действие обратное умножению. Мы выполняем деление для того, чтобы найти неизвестный множитель. Например:

Если нам неизвестен множитель 2, то мы будем его искать с помощью деления. Заменим множитель 2 на переменную x.

А теперь подробно рассмотрим ниже, что же такое деление рациональных чисел.

Деление двух рациональных чисел общие понятия.

Самое важное нужно правильно учитывать знаки при делении.

При делении двух рациональных чисел с одинаковыми знаками, результат будет с положительным знаком. При делении двух рациональных чисел с разными знаками, результат будет отрицательным.

Правила деления положительных и отрицательных рациональных чисел.

1. При делении двух положительных или двух отрицательных рациональных чисел, результат будет положительный. “Минус на минус дает знак плюс” или “Плюс на плюс дает знак плюс”
2. Выполняем деление по правилам в зависимости от того, какие числа делим (деление дробей, деление десятичных дробей, деление целых чисел и деление натуральных чисел).

Деление положительных и отрицательных рациональных чисел, примеры.

Выполните деление положительных и отрицательных рациональных чисел: а) \(\frac \div \frac<6><5>\) б) .

а) Вторую дробь переворачиваем по правилам деления дробей и между дробями ставим умножение . Смотрим возможно ли сократить дроби , в данном случае 3 у первой дроби в знаменателе и 6 у второй дроби в числители сокращается. Далее просчитываем знак ответа: “Минус на минус дает знак плюс.”

б) По правилам деления дробей вторую дробь переворачиваем и между дробями ставим умножение . Потом переходим к сокращению дробей числа 10 и 5 сокращаем на 5, а числа 11 и 22 сокращаем на 11. В итоге просчитываем знак, так как обе дроби имеют знак плюс, результат будет положительным числом.

Деление рациональных чисел с разными знаками.

При делении двух рациональных чисел с разными знаками, результат будет отрицательным.

Правила деления рациональных чисел рациональных чисел с разными знаками.

1. При делении двух рациональных чисел с разными знаками, результат будет отрицательный. “Минус на плюс дает знак минус” или “Плюс на минус дает знак минус”
2. Выполняем деление по правилам в зависимости от того, какие числа делим (деление дробей, деление десятичных дробей, деление целых чисел и деление натуральных чисел).

Пример деления рациональных чисел с разными знаками:

Выполните деление рациональных чисел с разными знаками: а) б) .

а) Вторую дробь переворачиваем по правилам деления дробей и между дробями ставим умножение . Смотрим возможно ли сократить дроби . Сокращение возможно на число 5. У первой дроби в знаменателе 5, а у второй дроби в числители 15, оба числа делятся на 5. Получилась в результате подсчетов неправильная дробь переводи ее в правильную дробь. Далее просчитываем знак ответа: “Плюс на минус дает знак Минус.”

б) Дробь переворачиваем и деление заменяем умножением. Далее сокращаем дроби и результат у нас получается со знаком минус.