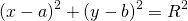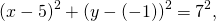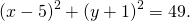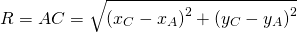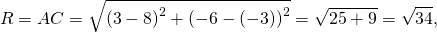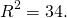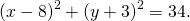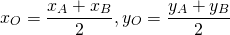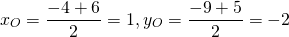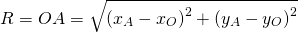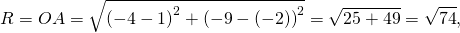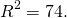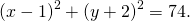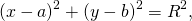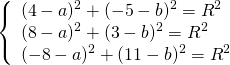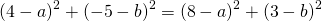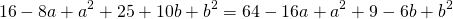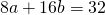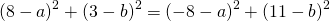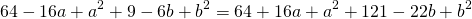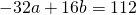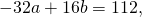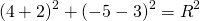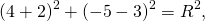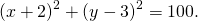Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, \(\mathrm
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = \(\mathrm<\frac1x>\) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ \mathrm <(x-2)^2+(y-1)^2=9>$$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: \( \mathrm
б) xy + 4 = 0
Выразим y из уравнения: \( \mathrm
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом \( \mathrm
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: \( \mathrm
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
\( \mathrm
Строим график для \( \mathrm
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) \(\mathrm<\frac<|x-1|><2>+2|y-2|=4>\)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
Решение задач по теме: «Уравнение окружностей»
Разделы: Математика
За неделю до проведения урока класс делится на четыре группы. Каждая готовит презентацию, отражающую название команды.
1. Образовательные:
2. Развивающие:
3. Воспитательные:
Ход урока
I. Организационный момент.
В начале урока выдается командам оценочный лист ( Приложение 1 ) с целью самостоятельной оценки учащимися степени участия каждого члена команды в подготовке к уроку и его проведении.
Рассказываются правила урока. За каждое правильное решение команде выдается лепесток определенного цвета:
все ответы верные – красный;
одна ошибка – зеленый;
две ошибки – жёлтый.
Лепестки крепятся на магнитную доску, образуя цветок.
Итоговая оценка выставляется с учетом этого бланка, а также учитывается количество и цвет набранных командой лепестков в цветке на доске.
2. Знакомство с командами (представление презентаций, Приложение 2 ).
3. Актуализация знаний учащихся.
– На последних уроках геометрии мы познакомились с еще одним способом решения задач МЕТОДОМ КООРДИНАТ.
Задавая фигуры уравнением и выражая в координатах геометрические соотношения, мы применяем алгебру к геометрии. Так мы поступили, когда выразили через координаты основную геометрическую величину – расстояние между точками, а затем, когда вывели уравнение окружности и прямой.
Пользуясь координатами, можно истолковывать уравнения и неравенства геометрически и таким образом применять геометрию к алгебре и анализу. Графическое изображение функций – первый пример такого применения метода координат
Метод координат в соединении с алгеброй составляет раздел геометрии, называемый “Аналитической геометрией”.
Сегодня я предлагаю еще раз поговорить об уравнении окружности и проследить, как алгебра помогает в решении геометрических задач.
4. Разминка.
– На доске записан ряд уравнений. Какие фигуры они задают?
Команды получают карточки с заданием. Время обдумывания 2мин.
По истечению времени идет опрос команд по очереди.
1  | 7.  |
2 . . | 8.  |
3.  | 9.  |
4.  | 10.  |
5.  | 11.  |
6.  | 12. |

Учитель показывает как, выделив полный квадрат, получить уравнение окружности.
Оценить результат работы команд.
Выясните, будет ли данные уравнения задавать окружность, если да, то укажите радиус и координаты центра. Если нет, то почему?
Каждая из команд получают свою карточку. Время 7 минут.
1.  | 1.  |
2.  | 2.  |
3.  | 3.  |
1.  | 1.  |
2  | 2  |
3  | 3  |
 |  |
 |  |
 |  |
 |  |
 |  |
 |  |
Последние уравнение в каждой карточке не задает окружность, и учащиеся поясняют почему. Оценить ответы.
1. Как могут взаимораспологаться две окружности? Дается время(3 мин.). Предлогается ребятам нарисовать различные варианты на ватмане и показать рисунки. После демонстрации и обсуждения всевозможных вариантов Предлогается следующая задача.
2. Как взаиморасположены линии заданные уравнениями?

Изобразите ответ на обратной стороне ватмана (на нем, заранее, нанесена система координат.)
Ответ:
O
Значит: первая внутри второй.
Результат этого задания оценивается следующим образом:
Команда, выполнившая первая – красный; вторая – зеленый; третья – желтый
После подведения итогов предлагается задача общая для всех команд.
Командам выдается карточка с кратким описанием условия. Текст задачи зачитывается.
Окружность задана уравнением 
Точка с координатами (5;4) является центром другой окружности касающейся первой внешним образом. Напишите уравнение этой окружности.
Вопросы для обсуждения:
-Поможет ли рисунок в решении задачи?
-Что можно узнать из уравнения первой окружности?
-Что надо знать, чтобы записать уравнение второй окружности?
-Как можно узнать радиус второй окружности?
Ответ:
Перед следующим заданием полезно повторить:
Какая окружность называется описанной около треугольника?
Что значит, точка принадлежит графику уравнения?
Что необходимо знать для написания уравнения окружности?
Написать уравнение окружности описанной около треугольника с заданными координатами вершин.
Какие, алгебраические, приемы могут быть использованы для решения поставленной задачи? (составление систем уравнений и приемы их решения).
| 3. С (3;-7) | 4. В (1;-4) |
| Д (8;-2) | К (4;5) |
| К (6;2) | Д (3;-2) |
1.  | 2.  |
3.    | 4 . . |
Следующую задачу решает учитель.
Задача: Что представляет собой множество точек плоскости, отношение расстояний от которых до двух данных точек есть величина постоянная?
Решение: Впервые эту задачу сформулировал и решил Аполлоний Пергский, (260-170 гг. до н.э.)
Решение получилось очень сложное – поскольку применены геометрические приемы. Однако в работах французского математика Рене Декарта эта задача решена более элегантно. Декарт применил метод координат.
Я предлагаю посмотреть на это решение. Итак, пусть даны две точки ,А и В и некоторое положительное число k, равное отношению расстояний до точки М.
1случай. Если k=1,тогда множество точек М есть серединный перпендикуляр к отрезку АВ.
2 случай. Пусть k целое не отрицательное число не равное 1
Для удобства решения возьмем k=2 , т.е. МА: МВ=2.
Введем систему прямоугольных координат. Совместим начало отсчета с точкой В. В качестве положительной полуоси x возьмем луч ВА. (рис.2)
Тогда получим следующие координаты точек: В(0,0), А(a,0), М(x,y). Пусть a=3 опять для простоты рассуждений.
Тогда, пользуясь формулами расстояния между двумя точками, запишем:

Получили уравнение окружности с центром в точке (-1;0) и радиусом r=2.
Значение радиуса не случайно вспомним, что мы выбрали k=2.
Решая задачу в общем виде т.е. при условии ,что точка А имеет координаты (a;0) и k

Такая окружность называется окружностью Апполония.
Подводится итог урока. Выставляются оценки.
Как составить уравнение окружности примеры
Написать уравнение окружности
Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.
1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.
Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:
Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:
2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).
Так как центр окружности — точка A(8; -3), то a=8, b=-3.
Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.
Следовательно, уравнение данной окружности
3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).
Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка
Центр окружности — точка O(1;-2). Значит, a=1, b=-2.
Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,
Таким образом, уравнение окружности с диаметром AB —
4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).
Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение
получаем систему уравнений:
Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим
Приравняем правые части 2-го и 3-го уравнений:
на -1 и сложив результат почленно с уравнением
получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:
Следовательно, уравнение окружности, проходящей через три данные точки —
5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).
Решение аналогично решению задания 4. В результате получим уравнение
Уравнение окружности.
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.
Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.
Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
Уравнение с двумя переменными и его график. Уравнение окружности
п.1. Понятие уравнения с двумя переменными
Мы уже знакомы со многими функциями и умеем их записывать в виде формул:
y = 2x + 5 – прямая, y = 5x 2 + 2x – 1 – парабола, \(\mathrm \) – гипербола.
Если записать такое выражение: x 2 (x + y) = 1 – y – в нём тоже есть две переменные x и y, и постоянная 1.
Для наших примеров:
F(x; y) = 2x – y + 5 = 0 – прямая
F(x; y) = 5x 2 + 2x – y – 1 = 0 – парабола
F(x; y) = \(\mathrm \) – y = 0 – гипербола
F(x; y)=x 2 (x + y) + y – 1 = 0 – некоторая кривая (график — ниже).
п.2. Обобщенные правила преобразования графика уравнения
Пусть F(x; y) = 0 – исходный график некоторой функции
Симметричное отображение относительно оси OY
Симметричное отображение относительно оси OX
Центральная симметрия относительно начала координат
Параллельный перенос графика на a единиц вправо
Параллельный перенос графика на a единиц влево
Параллельный перенос графика на b единиц вниз
Параллельный перенос графика на b единиц вверх
Сжатие графика к оси OY в a раз
Сжатие графика к оси OX в b раз
F(x; by) = 0
0 Например:
Окружность с центром в точке O(2; 1) и радиусом R = 3 задаётся уравнением: $$ \mathrm $$
п.4. Примеры
Пример 1. Постройте график уравнения:
а) 2x + 7y – 14 = 0
Выразим y из уравнения: \( \mathrm =-\frac + 2 > \) – это прямая
б) xy + 4 = 0
Выразим y из уравнения: \( \mathrm > \) – это гипербола
в) ( x+ 2) 2 + y 2 = 4
Это – уравнение окружности с центром O(–2; 0), радиусом \( \mathrm =2> \)
г) x 2 + 5y – 2 = 0
Выразим y из уравнения: \( \mathrm > \) – это парабола
Пример 2*. Постройте график уравнения:
а) 2|x| + 5y = 10
\( \mathrm =-\frac25|x|+2> \)
Строим график для \( \mathrm \), а затем отражаем его относительно оси OY в левую полуплоскость.
б) 3x + |y| = 6
|y| = –3x + 6
Строим график для y > 0: y = –3x + 6, а затем отражаем его относительно оси OX в нижнюю полуплоскость.
в) |x| + |y| = 2
|y| = –|x| + 2
Строим график для x > 0, y > 0: y = –x + 2, а затем отражаем его относительно осей OX и OY.
г) |x – 1| + |y – 2| = 4
Получим тот же ромб (квадрат), что и в (в), но его центр будет перенесен из начала координат в точку O(1; 2).
д) \(\mathrm +2|y-2|=4>\)
Ромб по x растянется в 2 раза по диагонали, а по y – сожмётся в 2 раза по диагонали.
Пример 3. Постройте график уравнения:
а) x 2 + y 2 + 4x – 6y + 4 = 0
Выделим полные квадраты:
(x 2 + 4x + 4) + (y 2 – 6y + 9) – 9 = 0
(x + 2) 2 + (y – 3) 2 = 3 2 – уравнение окружности с центром (–2; 3), радиусом 3.
http://urok.1sept.ru/articles/412785
http://b4.cooksy.ru/articles/kak-sostavit-uravnenie-okruzhnosti-primery