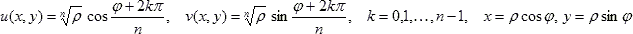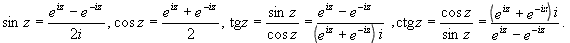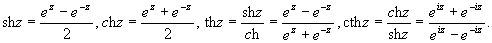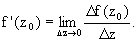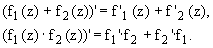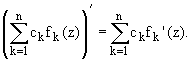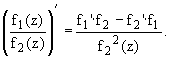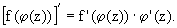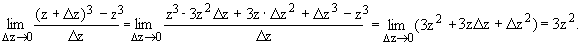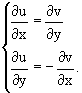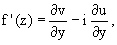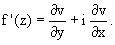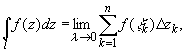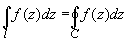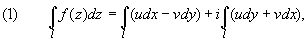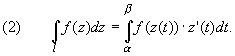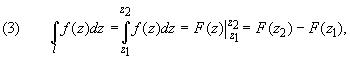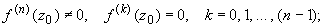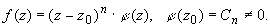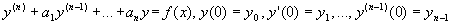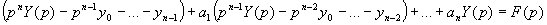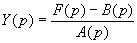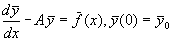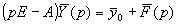Примеры решений задач по теории функций комплексной переменной
В этом разделе вы найдете готовые задания по разным разделам ТФКП (теории функций комплексной переменной): проверка аналитичности функций, восстановление функции по одной из частей (мнимой или действительной), разложение в ряд, вычисление вычетов, нахождение интегралов разных типов.
Если вам нужна помощь в выполнении своей домашней работы по ТФКП, мы будем рады помочь: стоимость задания от 80 рублей, срок от 1 дня, гарантия месяц, подробное оформление, отзывы. Узнайте подробнее о том, как мы выполняем задания по ТФКП на заказ.
Еще полезные ссылки для изучения:
Гармонические (аналитические) функции. Решения задач
Задача 1. Показать, что данные функции $u(x,y)$ и $v(x,y)$ гармонические. Найти по заданной функции $u(x,y)$ или $v(x,y)$ ей сопряженную: $u(x,y)=\cos x ch y, v(0,0)=0.$
Задача 2. Исследуйте на моногенность и голоморфность $f(z) = (Re z)^2$.
Задача 3. Найти аналитическую функцию $f(z)$, если задана ее мнимая часть $Im f(z)=10xy-6y$, $f(1/5)=-1.$
Задача 4. Доказать, что $f(z)=\sin(z/3)$ — аналитическая функция и найти производную в точке $z_0=\pi i/6.$
Ряды Лорана и Тэйлора. Решения задач
Задача 5. Разложить функцию $f(z)$ по степеням $(z-z_0)$ в ряд Тейлора или Лорана во всех областях на плоскости, где такое разложение возможно. $$f(z)=\frac
Задача 6. Разложить данную функцию в ряд Лорана в заданном кольце комплексной плоскости. Указать область сходимости полученного ряда: $$f(z)=\frac<1>
Задача 7. Определить круг сходимости и исследовать сходимость в данных точках. $$\Sigma_
Вычеты функции и их применение. Решения задач
Задача 8. Найти вычеты функции относительно её полюсов: $$ f(z) =\frac<1>
Задача 9. Вычислить интеграл по замкнутому контуру с помощью вычетов: $$\int_
Задача 11. Вычислить контурный интеграл с помощью основной теоремы Коши о вычетах: $$\int_
Интегралы от функций комплексного переменного. Решения задач
Задача 12. Вычислить интеграл от функции комплексного переменного по данной кривой: $$\int_
Конформные отображения. Решения задач
Задача 13. Найдите взаимно-однозначное конформное отображение, переводящее $D_1$ на $D_2$: $$D_1=\<|z| \lt 1\>, \quad D_2=\<|z| \lt 1, Im z \gt 0\>. $$
Курс по теории функций комплексного переменного
Небольшой теоретический курс по теории функций комплексного переменного.
Различные формы представления комплексных чисел. Арифметические операции с комплексными числами
Комплексным числом z называется упорядоченная пара действительных чисел x и y.
Первое из них x называется действительной частью комплексного числа z и обозначается Rez, x = Rez;
второе число y называется мнимой частью комплексного числа z и обозначается Imz, y = Imz.
Два комплексных числа равны тогда и только тогда, когда равны их действительные и мнимые части:
Алгебраическая форма записи комплексного числа
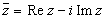
называется комплексно сопряженным числу
Комплексное число z = x + iy естественно изображать в виде точки на плоскости с декартовыми координатами (x, y).
Если x и y — декартовы координаты точки плоскости, то, перейдя на плоскости к полярным координатам (r, j) и воспользовавшись связью
x = rcosj, y = rsinj
получим тригонометрическую форму записи комплексного числа:
z = r (cosj + isinj) .
При этом число r называют модулем комплексного числа, |z| = r, а число j — аргументом комплексного числа,
Arg z = arg z+2kp= j.
При решении задач для вычисления аргумента удобно пользовааться схемой, приведенной ниже:
Используя формулу Эйлера
получим показательную форму записи комплексного числа:
Арифметические операции c комплексными числами определяются следующим образом:
Элементарные функции комплексного переменного
Значение целой положительной степени комплексного аргумента, значение функции f(z) = z n , проще всего вычислять в тригонометрической форме.
Если z = x + iy = r (cosj + isinj ), то для любого целого положительного числа n имеет место формула:
w = f(z) = z n = r n (cos nj + isin nj ).
Если w = f (z) = f (x + iy) = u(x, y) + iv(x, y), то
u(x, y) = r ncos nj , u(x, y) = r nsin nj.
Корнем n-й степени из комплексного числа z называется число
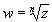
Для любого комплексного числа z существует n комплексных чисел w таких, что wn = z.
Значение корня, т.е. значение функции
проще всего вычислять в тригнометрической форме.
Если z = x + iy = r (cosj + isinj), то для любого целого положительного числа n имеет место формула:
является многозначной функцией _ каждому значению аргумента отвечает n различных значений корня.
Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то
Если z = x + iy = r (cosj + isinj ), то значения функции f(z) = exp(z) вычисляются по формуле
f(z) = ez = ex+iy = e xe iy = ex (cosy + isiny).
Если w = f(z) = f(x + iy) = u(x, y) + iv(x, y), то
u(x,y) = ex cosy , v(x,y) = ex siny.
Тригонометрические функции комплексного аргумента определяются формулами:
Гиперболические функции комплексного переменного определяются совершенно так же, как функции в действительной области:
Логарифмом комплексного числа z называется такое число w, что
Значения логарифмической функции f(z) = Ln(z) вычисляются по формуле
Ln(z) = ln(|z|) + iArg z = ln(|z|) + iarg z + 2kp i, k = 0,1,2.
Величину ln(|z|) + iarg z называют главным значением логарифма.
Функция f(z) = Ln(z) является многозначной функцией _ каждому значению аргумента отвечает бесконечное множестворазличных значений логарифма.
Показательная (f(z) = az) и степенная (f(z) = za) функции комплексного переменного определяются с помощью логарифма — для любых комплексных чисел a и z справедливо:
Значения обратных тригонометрических функций комплексного переменного вычисляются по формулам:
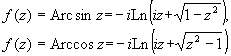
Дифференцирование функций комплексного переменного
Производная функции комплексного переменного определяется, как и производная в действительной области:
z0, Dz _ комплексные и Df(z0) = f(z0+Dz) — f(z).
Используя это определение и свойства пределов, несложно убедиться в справедливости следующих правил дифференцирования.
1. Сумма и произведение дифференцируемых в точке функций, есть функция и справедливы равенства:
2. Частное дифференцируемых в точке функций, при условии, что знаменатель в точке не равен нулю, есть дифференцируемая в этой точке функция, :
3. Сложная функция f(j (z)) дифференцируема в точке z0, если в этой точке дифференцируема функция j (z), а функция f(u) дифференцируема в точке u0,
где u0 = j (z0) и u = j (z). При этом в точке z0 имеет место формула:
Для элементарных функций комплексного переменного справедливы формулы дифференцирования, установленные для действительных значений аргумента.
Например, рассмотрим функцию f(z) = z3.
По определению производной для любой точки z, принадлежащей комплексной области, записываем:
Предел существует для любой точки z, принадлежащей комплексной области и
Аналогично можно получить:
(zn)’ = nzn-1 (n — действительное число).
Если f(z) = f(x+iy) = u(x, y) + iv(x, y), т.е. u(x, y) = Re f(z) и v(x, y) = Im f(z),
то справедливы следующие утверждения:
1. Если функция f(z) дифференцируема в точке, то в этой точке существуют частные производные ее действительной и мнимой частей
u(x, y) = Re f(z), v(x, y) = Im f(z)
и выполняется условие Коши-Римана:
2. Если u(x, y) и v(x, y) дифференцируемы в точке (x0, y0) (имеют непрерывные частные производные в этой точке) и выполняется условие Коши-Римана, то функция f(z) = f(x+iy) = u(x, y) + iv(x, y) дифференцируема в точке z0 = x0+ iy0.
3. Производная дифференцируемой функции может быть записана по одной из формул:
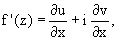
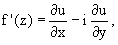
Интегралы в комплексной области.
Интегралом от функции комплексного переменного называется предел последовательности интегральных сумм; функция при этом определена на некоторой кривой l, кривая предполагается гладкой или кусочно-гладкой:
где 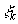
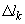
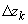
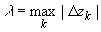
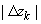
.gif)
кривая l разбивается произвольным образом на n частей .gif)
На кривой выбрано направление, т.е. указаны начальная и конечная точки.
В случае замкнутой кривой l = C
интегрирование происходит в положительном направлении, т.е. в направлении обхода, оставляющем слева конечную область, ограниченную контуром С.
Существует несколько способов вычисления интегралов в комплексной области.
1 способ. Интеграл вычисляется сведением к криволинейным интегралам от функций действительных переменных — примененяются формулы:
где f(z) = u + iv, u = Re f(z), v = Im f(z).
2 способ. Интеграл вычисляется сведением к определенному интегралу (путь интегрирования l задается в параметрической форме z = z(t)) — применяется формула:
3 способ. Вычисление интегралов от аналитической функции в односвязных областях — примененяеется формула:
где F(z) — первообразная для f(z).
Нули аналитической функции.
Пусть функция f (z) является аналитической в точке z0. Точка z0 называется нулем функции f (z), если ее значение в этой точке равно нулю, т.е. f (z0) = 0.
В разложении функции в ряд Тейлора в окрестности нуля этой функции (т. z0) отсутствует свободный член: С0 = f(z0) = 0.
Если при этом в разложении отсутствуют и слагаемые, содержащие степени разности (z-z0) до n-ой степени, т.е. разложение имеет вид: 
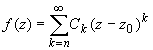
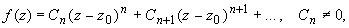
Нуль первого порядка (n = 1) называется простым нулем.
Следующие условия являются необходимым и достаточным условиями нуля порядка n функции f (z) в точке z0:
a).
b). представление функции в виде произведения:
Порядок нуля в точке z0 функции, полученной в результате перемножения аналитических функций
f (z) = f1(z) f2(z) равен сумме порядков нуля (n1 + n2) в этой точке функций сомножителей
( n1 — порядок нуля в точке z0 функции f1(z), n2 — порядок нуля в точке z0 функции f2(z) ).
Изолированные особые точки функции комплексного переменного.
Точка z0, принадлежащая области комплексных чисел, называется изолированной особой точкой функции f(z), если 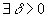
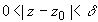
Изолированная особая точка z0 функции f(z) называется:
устранимой особой точкой, если 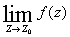
полюсом, если 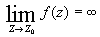
существенно особой точкой, если .gif)
Для того чтобы особая точка функции f(z) была ее устранимой особой точкой, необходимо и достаточно, чтобы в разложении функции в ряд Лорана в окрестности этой точки отсутствовала главная часть. Это означает, что если z0 — устранимая особая точка, то ряд Лорана функции f(z) имеет вид: 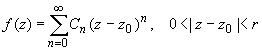
для z0 — конечной точки, принадлежащей области комплексных чисел.
Для того чтобы особая точка функции была полюсом, необходимо и достаточно, чтобы главная часть ряда Лорана функции в окрестности этой точки содержала конечное число членов.
Ряд Лорана функции f(z) в случае z0-полюс имеет вид:
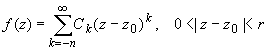
если z0 принадлежит области комплексных чисел.
Номер старшего члена главной части ряда Лорана функции в ее разложении в окрестности полюса называется порядком полюса.
Так, точка z0 является полюсом порядка n функции f(z), если в разложении (2) 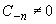
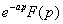
Рассмотри задачу Коши:
a1, a2, . an — постоянные.
Алгоритм решения задачи Коши для уравнений операционным методом состоит в следующем. Обрзначим Y (p) и F (p) изображения для y (x) и f (x).
Тогда по основным свойствам преобразования Лапласа, переходя к изображениям, получим:
или, A (p)Y (p) + B (p) = F (p), где A (p) и B (p) — многочлены.
и искомое решение задачи Коши y (x) является оригиналом для Y (p).
Совершенно аналогично операционное исчисление применяется к решению задачи Коши для систем линейных дифференциальных уравнений с постоянными коэффициентами. Рассмотри задачу Коши:
A- постоянна матрица размерности n.n.
Алгоритм решения задачи Коши для систем операционным методом состоит в следующем.
Обозначим 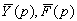
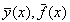
.gif)
.gif)
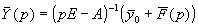
где E — единичная матрица, 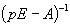
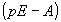
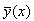
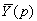
http://hub.exponenta.ru/post/kurs-po-teorii-funktsiy-kompleksnogo-peremennogo828

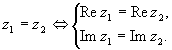
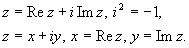
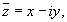
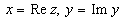
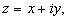
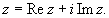
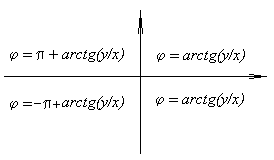
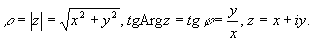
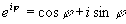
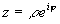
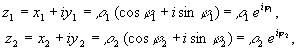
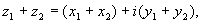
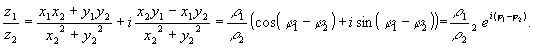
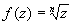
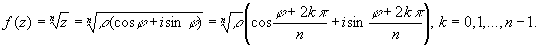
.gif)