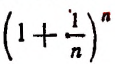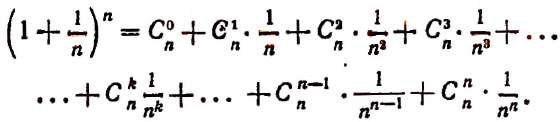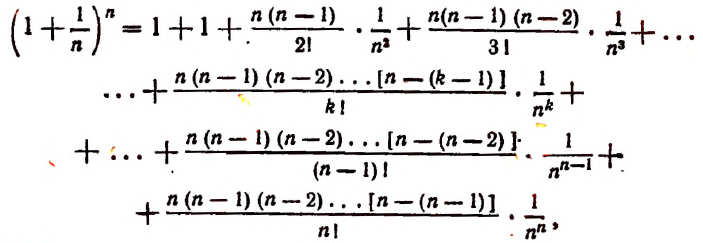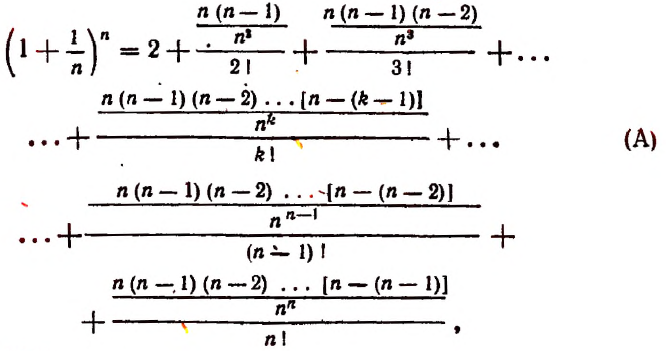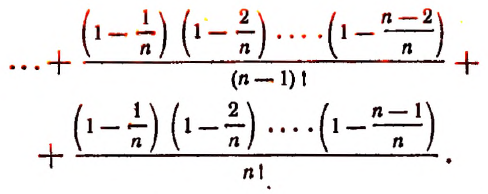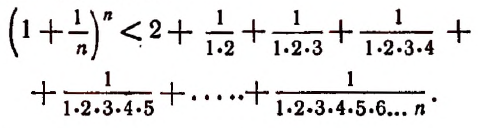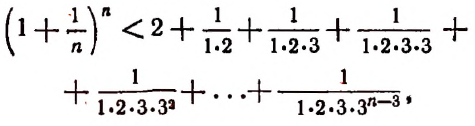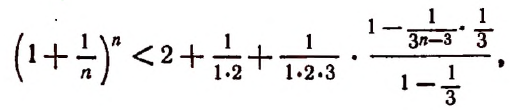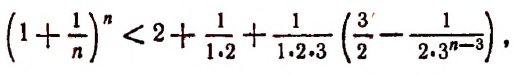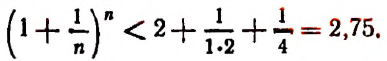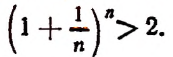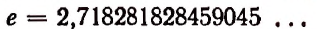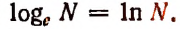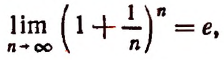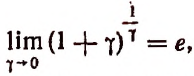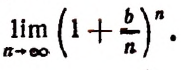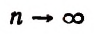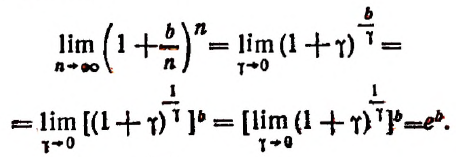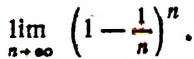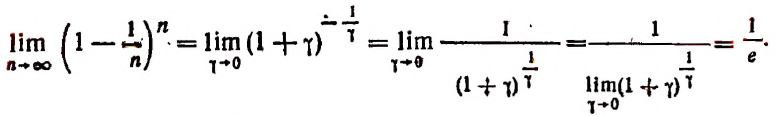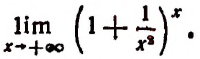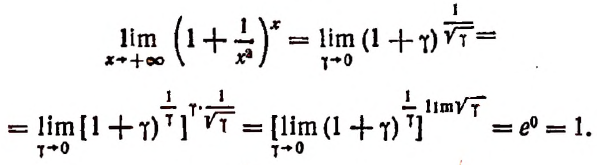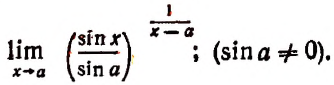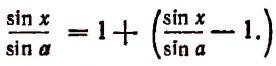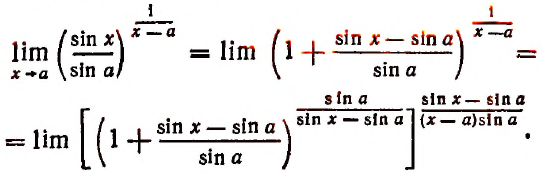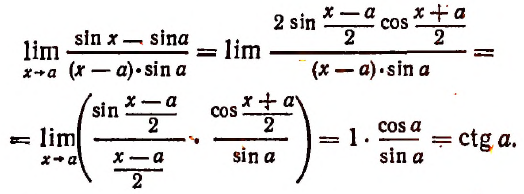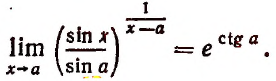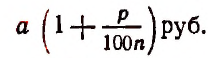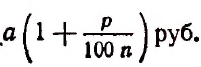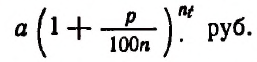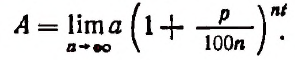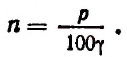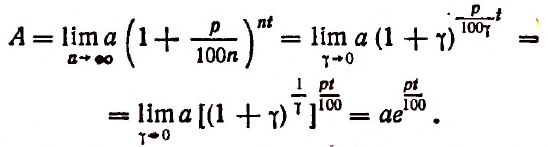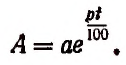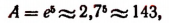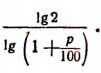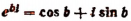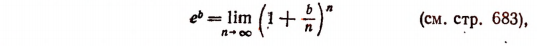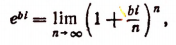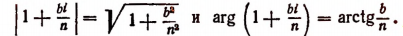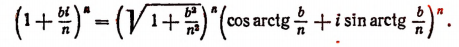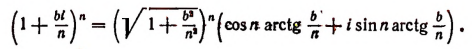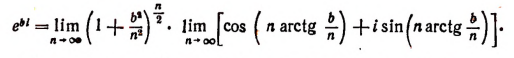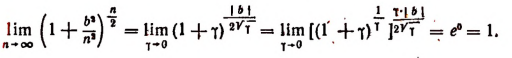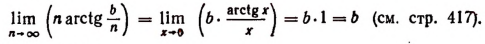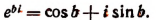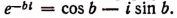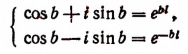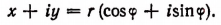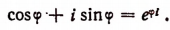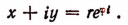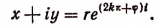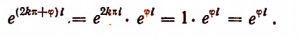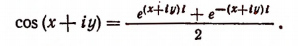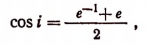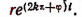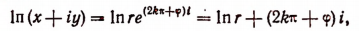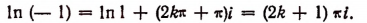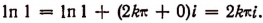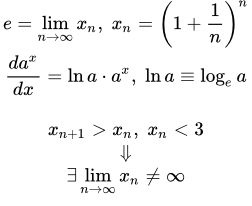Число е в математике и его применение с примерами решения
Возникновение числа е:
в котором n — натуральное число.
Изучение этого выражения необходимо для решения очень многих крайне важных задач (см., например, следующий параграф и главу «Производная, дифференциал, интеграл и их простейшие применения»).
Если мы станем натуральное число n неограниченно увеличивать, то величина выражения
станет величиной переменной. Эта переменная не стремится к единице, как это может показаться на первый взгляд. Действительно, мы сейчас убедимся в том, что при возрастании натурального числа n значение выражения
будет монотонно* возрастать, начиная со значения, равного двум. Например,
- Последовательность
называется возрастающей, если
неубывающей, если
убывающей, если
невозрастающей, если
Все такие последовательности называются монотонными.
Чтобы доказать, что переменная
монотонно возрастает при возрастании n, применим формулу бинома Ньютона:
Перепишем эту формулу в следующем виде:
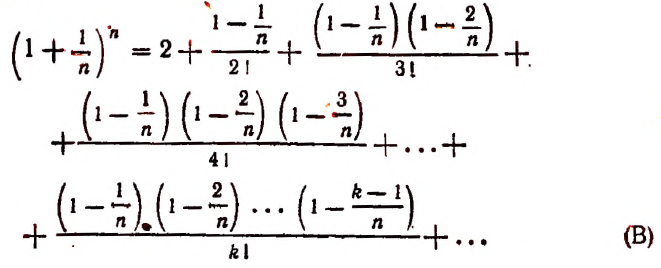
Все слагаемые в правой части этого равенства положительны.
При возрастании числа n правая часть этого равенства будет монотонно возрастать, так как будет возрастать число слагаемых и каждое слагаемое, начиная со второго.
Значит, доказано, что переменная 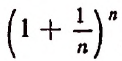
Теперь докажем, что, несмотря на то что переменная 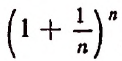
Из формулы (В) видно, что
Тем более будет верным неравенство
К сумме, написанной в квадратных скобках, применим формулу суммы членов конечной геометрической прогрессии. Тогда получим:
и тем более будет верным неравенство
Кроме этого, из формулы (А) видно, что всегда
Теперь перейдем к самому важному выводу.
Мы доказали, что переменная 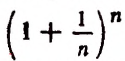
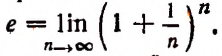
Число е выражается бесконечной непериодической десятичной дробью. Первые цифры этой дроби идут в таком порядке:
Напомним, что логарифмы по основанию е называются натуральными и обозначаются символом 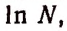
Применения числа е
Исходя из полученного равенства
можно доказать, что
где 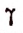
Последнее равенство можно сформулировать так:
Степень, основанием которой служит единица плюс бесконечно малое слагаемое 7, а показателем величина, обратная этому слагаемому, стремится к числу е, как к своему, пределу (доказательство опускается).
Обратим внимание на то, что основание этой степени стремится к единице, но, несмотря на это, сама степень не стремится к единице.
Рассмотрим пределы степеней, в которых основанием служит единица плюс бесконечно малое слагаемое, а показатель есть величина, обратная этому слагаемому.
Примеры:
1. Найти
Решение:
Полагая 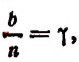
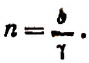
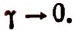
2. Найти
Полагая 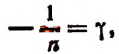
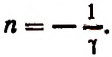
3. Найти
Полагая 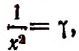
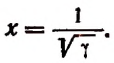
4. Найти
Представим 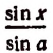
Здесь первое слагаемое есть единица, а второе, стоящее в скобках, есть величина бесконечно малая при
Таким образом, получим:
В квадратных скобках мы имеем степень, основанием которой является единица плюс бесконечно малое слагаемое, а показатель степени есть величина, обратная этому бесконечно малому слагаемому. Предел такой степени, как мы знаем, равен числу е.
Теперь найдем предел показателя степени, в который возводится выражение, стоящее в квадратных скобках:
Задачи:
1. Пусть банк принял вклад в a руб. и обязался присоединять процентные деньги к вкладу через каждую 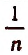
Одну n-ю часть года назовем установленным промежутком времени. Тогда один год будет содержать n, a t лет nt таких промежутков.
К концу первого промежутка времени вклад обратится в
Действительно, за первый промежуток времени процентные деньги, подлежащие присоединению к вкладу, будут равны 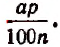
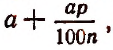
Обратим внимание на то, что для получения возросшей суммы за один промежуток времени достаточно вклад, имевшийся в начале промежутка, умножить на 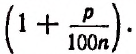
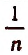
Значит, чтобы получить возросшую сумму к концу второго промежутка времени, достаточно вклад, образовавшийся к началу второго промежутка времени, умножить на множитель процентного наращения и т. д.
Итак, первоначальный вклад в а руб. обратится через t лет в
Теперь вообразим, что 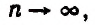
Полагая 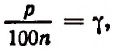
Итак, для органического роста вклада получилась следующая формула:
Например, при а = 1, р = 5 и f = 100
т. е. один рубль превращается через 100 лет приблизительно в 143 руб., если органический рост происходит по 5 годовых процентов.
2. Лесная делянка содержит в данный момент а куб. м древесины. Сколько окажется на этой делянке древесины через t лет, если органический рост древесины происходит по р годовых процентов.
Oтв. 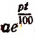
3. Численность населения города увеличивается ежегодно на р% (по отношению к началу года). Через сколько лет численность населения удвоится?
Отв.
Формула Эйлера
Формула Эйлера
В заключение этой главы приведем еще одно важное соотношение, найденное гениальным Эйлером, устанавливающее связь между тригонометрическими функциями и показательной функцией. Было доказано, что
где b — любое действительное число.
Обобщая этот результат, примем по определению, что
где b — любое действительное число, a i — мнимая единица. Теперь вычислим предел правой части последнего равенства.
Комплексное число 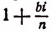
Пользуясь формулой Муавра, найдем, что
Вычислим каждый из пределов, входящих в правую часть последней формулы. Обозначив 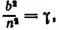
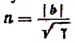
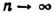
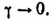
Далее, обозначим 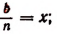
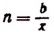
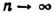
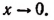
Эта формула и носит название формулы Эйлера.
Следствия из формулы Эйлера
1. Полагая в формуле Эйлера вместо b число 2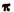
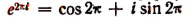
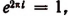
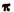
2. Полагая в формуле Эйлера вместо b число — b, получим, что
3. Пользуясь формулой Эйлера, можно представить любое комплексное число еще в одной новой форме.
Действительно, обозначив модуль комплексного числа х + iy буквой r, а главное значение аргумента буквой 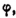
Но по формуле Эйлера
Выражение 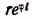
Справедливой будет и следующая запись:
4. Исходя из формулы Эйлера, мы можем находить тригонометрические функции от комплексного числа.
Действительно, обобщая формулу 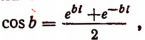
Полагая в последней формуле, например, х = 0 и у = 1, получим:
т. е. получим, что косинус мнимой единицы представляет собой действительное число.
5.Опираясь на формулу Эйлера, можно показать, что логарифм любого действительного или мнимого числа имеет в области комплексных чисел бесконечное множество различных значений. Представим комплексное число х + iy в показательной форме
где k — любое целое число.
Под выражением In r здесь понимается лишь действительное значение логарифма положительного числа r, которое легко вычисляется по таблицам логарифмов.
Примеры:
1. Модуль числа— 1 равен 1, а главное значение аргумента равно 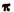
2. Модуль числа 1 есть 1, а главное значение аргумента 0. Поэтому
Под выражением In 1, написанным в левой части последнего равенства, подразумеваются все возможные комплексные значения логарифма единицы.
Под таким же выражением In 1, написанным в правой части, подразумевается лишь одно действительное значение логарифма единицы, т. е. нуль.
Числа е и 
С помощью этих чисел выражаются многие законы, по которым происходят процессы в природе. Числа е и 
Дополнение к числу е

Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Число e – его смысл и доказательство сходимости последовательности
Определение числа e
Этот предел является частным случаем второго замечательного предела. Число e иногда называют числом Эйлера или числом Непера. Это самое используемое число в математическом анализе. Оно примерно равно
.
Число e можно представить в виде ряда:
.
Далее приводится объяснение, почему оно так популярно в математике, и дается доказательство существования конечного предела (1).
Смысл числа e
С развитием механики, возникла потребность в вычислении мгновенной скорости движения тел. Для определения скорости v , мы должны взять разность значений координат x в два момента времени и разделить на промежуток времени между ними:
.
По этой формуле, однако, мы не получим мгновенного значения скорости, а получим ее среднее значение в промежутке времени между и . Чтобы найти мгновенную скорость, мы должны положить . Но тогда знаменатель дроби станет равным нулю. Таким образом, эта задача не решается методами классической алгебры.
При попытке решить эту задачу, возникла новая математическая дисциплина – математический анализ. В нем, мгновенная скорость в момент времени t определяется как предел, к которому стремится отношение при , стремящемся к нулю. Этот предел называется производной x по t .
Таким образом, производная является одним из самых важных понятий в математическом анализе. Поэтому необходимо уметь вычислять производные. Оказывается, что если мы найдем производную показательной функции , то ее вычисление сводится к вычислению второго замечательного предела, аналогичного пределу последовательности (1), и выражается через число e :
.
Тогда, если за основание степени a взять число e , то производная будет иметь наиболее простой вид:
.
В связи с этим, в математическом анализе, за основание степени, там где это возможно, выбирают именно число e . Показательная функция с основанием e называется экспонентой. Логарифм по основанию e называется натуральным логарифмом и имеет специальное обозначение . Любую другую показательную функцию (с другим основанием) можно выразить через экспоненту:
.
Таким образом, смысл применения числа e заключается в том, что через него выражается производная показательной функции, и без него просто нельзя обойтись.
Но прежде, чем применять число e , нужно доказать, что оно существует. То есть нужно доказать, что существует конечный предел последовательности при n стремящемся к бесконечности: .
Доказательство сходимости последовательности
Здесь мы покажем, что последовательность с общим членом
(2)
имеет конечный предел. Для этого мы применим теорему Вейерштрасса о пределе монотонной последовательности. Тогда нам нужно доказать, что
1) последовательность (2) монотонна;
2) последовательность (2) ограничена.
Доказательство можно выполнять различными способами.
Применение бинома Ньютона
Рассмотрим последовательность с общим членом
(2) .
Докажем, что она строго возрастает. Для этого применим формулу бинома Ньютона:
Здесь
– биноминальные коэффициенты.
Подставим и выполним преобразования. Тогда элемент запишется в виде суммы положительных членов:
.
Выполняя деление в каждом члене на , имеем:
(3)
Для элемента имеем сумму положительных членов:
Далее замечаем, что
Таким образом, каждый член в , начиная с третьего по n + 1 -ый, больше соответствующего члена в . Кроме этого, в на один положительный член больше. Поэтому
То есть последовательность строго возрастает.
Докажем, что эта последовательность ограничена. Поскольку она возрастает, то снизу она ограниченна значением . Докажем, что последовательность ограничена сверху. Для этого замечаем, что
Тогда
Далее замечаем, что . Тогда
.
Применим формулу суммы членов геометрической прогрессии:
.
Отсюда получаем ограниченность :
.
Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.
Применение неравенства Бернулли
Снова рассматриваем последовательность
(2) .
Докажем ее монотонность и ограниченность применяя неравенство Бернулли. При и при натуральном , имеет место следующее неравенство:
(4) .
Докажем с его помощью, что последовательность строго возрастает. Выпишем ее элементы в следующем виде:
, .
Тогда
.
Преобразуем второй множитель и применим неравенство Бернулли:
;
.
Поскольку , то строгое возрастание последовательности доказано.
Докажем, что последовательность ограничена. Поскольку она возрастает, то нам нужно доказать ее ограниченность сверху. Для четных n , является натуральным числом. Имеем:
;
.
Отсюда следует, что элементы последовательности с четными номерами ограничены:
.
Если n нечетно, то используем тот факт, что последовательность строго возрастает. Тогда четно. Поэтому и при нечетных n , элементы последовательности ограничены:
.
Итак, мы показали, что последовательность монотонна и ограничена. Тогда по теореме Вейерштрасса, она имеет конечный предел.
Использование вспомогательной последовательности
Для исследования сходимости исходной последовательности, иногда бывает удобно взять вспомогательную последовательность, которую легче исследовать. При этом предел исходной последовательности должен выражаться через предел вспомогательной.
В нашем случае, для исследования сходимости последовательности
(2) ,
возьмем вспомогательную последовательность
(5) .
Покажем, что она строго убывает. Для этого используем неравенство Бернулли:
(4) .
Имеем:
;
.
Поскольку , то отсюда следует, что последовательность строго убывает.
Покажем, что ограничена. Поскольку она убывает, то сверху она ограничена значением . Покажем, что последовательность ограничена снизу. Снова применяем неравенство Бернулли:
;
.
Поскольку последовательность монотонна и ограничена, то, по теореме Вейерштрасса, она имеет конечный предел.
Элементы исходной последовательности выражаются через :
.
Далее замечаем, что
.
Применяем теорему о пределе частного числовой последовательности:
.
Поскольку последовательность имеет конечный предел, то и исходная последовательность имеет конечный предел.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов . Опубликовано: 25-03-2019
Число Эйлера (e)
Число e (или, как его еще называют, число Эйлера) – это основание натурального логарифма; математическая константа, являющаяся иррациональным числом.
Способы определения числа e (формула):
1. Через предел:
Второй замечательный предел:
Альтернативный вариант (следует из формулы Муавра – Стирлинга):
2. Как сумма ряда:
Свойства числа e
1. Предел обратного числа e
2. Производные
Производной экспоненциальной функции является экспоненциальная функция:
Производной натуральной логарифмической функции является обратная функция:
3. Интегралы
Неопределенным интегралом экспоненциальной функции e x является экспоненциальная функция e x .
Неопределенный интеграл натуральной логарифмической функции loge x:
Определенный интеграл от 1 до e обратной функции 1/x равен 1:
Логарифмы с основанием e
Натуральный логарифм числа x определяется как базовый логарифм x с основанием e:
Экспоненциальная функция
Это показательная функция, которая определяется следующим образом:
Формула Эйлера
Комплексное число e iθ равняется:
где i – мнимая единица (квадратный корень из -1), а θ – любое действительное число.
http://1cov-edu.ru/mat-analiz/predel-posledovatelnosti/chislo-e/
http://microexcel.ru/chislo-e/
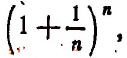
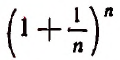
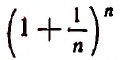

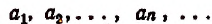 называется возрастающей, если
называется возрастающей, если 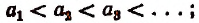 неубывающей, если
неубывающей, если 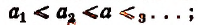 убывающей, если
убывающей, если 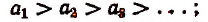 невозрастающей, если
невозрастающей, если 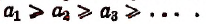 Все такие последовательности называются монотонными.
Все такие последовательности называются монотонными.