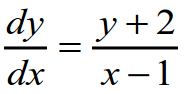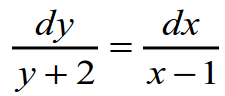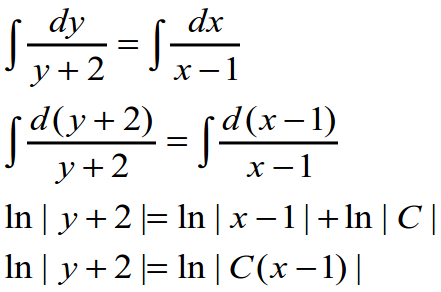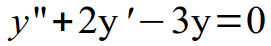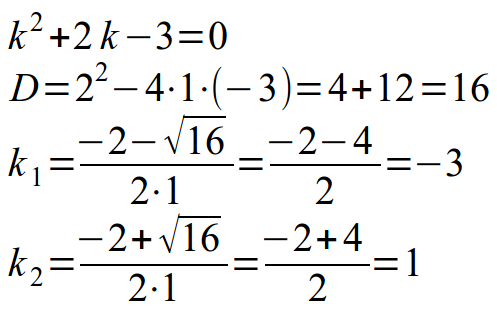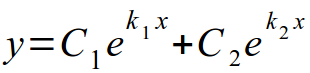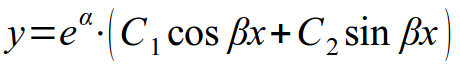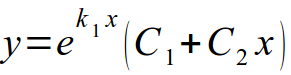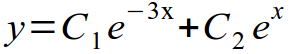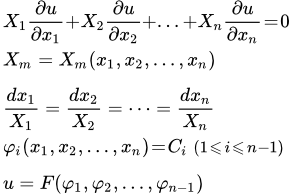Дифференциальные уравнения. Что это?
| Срок выполнения | от 1 дня |
| Цена | от 100 руб./задача |
| Предоплата | 50 % |
| Кто будет выполнять? | преподаватель или аспирант |
Вы уже имеете находить производные и интегралы? Тогда настало самое время, чтобы перейти к более сложной теме, а именно, решению дифференциальных уравнений (ДУ, в простонародье диффуров). Но не все так страшно, как кажется на первый взгляд.
Дифференциальное уравнение: что это такое?
Дифференциальное уравнение (ДУ) – это уравнение, которое вместе с самой функцией (и ее аргументами), содержит еще и ее производную или несколько производных.
Дифференциальное уравнение: что нужно знать еще?
Первое (и главное), что понадобится, это умение правильно определять тип дифференциального уравнения. Второе, но не менее важное, это умение хорошо интегрировать и дифференцировать.
Не секрет, что дифференциальные уравнения бывают разных типов. Но… для начала отметим, что ДУ бывают разных порядков. Порядок ДУ — это порядок высшей производной, входящей в дифференциальное уравнение. Классификацию ДУ согласно порядку уравнения можно посмотреть в следующей таблице:
| Порядок уравнения | Вид уравнения | Пример |
|---|---|---|
| I | 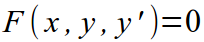 | 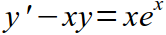 |
| II | 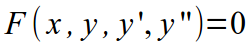 | 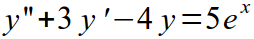 |
| … | … | … |
| n | 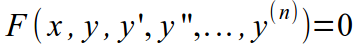 | 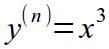 |
Наиболее часто приходится иметь дело с ДУ первого и второго порядка, реже третьего. В 99% случаев в задачах встречаются три типа ДУ первого порядка: уравнения с разделяющимися переменными, однородные уравнения и линейные неоднородные уравнения. Иногда еще встречаются более редкие типы ДУ: уравнения в полных дифференциалах, уравнения Бернулли и др. Среди ДУ второго порядка часто встречаются уравнения, приводящиеся к ДУ первого порядка, линейные однородные и неоднородные уравнения с постоянными коэффициентами.
Дифференциальное уравнение: решение – что это значит и как его найти?
При решении ДУ нам предлагается найти либо общее решение (общий интеграл), либо частное решение. Общее решение y = f(x, C) зависит от некоторой постоянной ( С — const), а частное решение не зависит: y = f(x, C0).
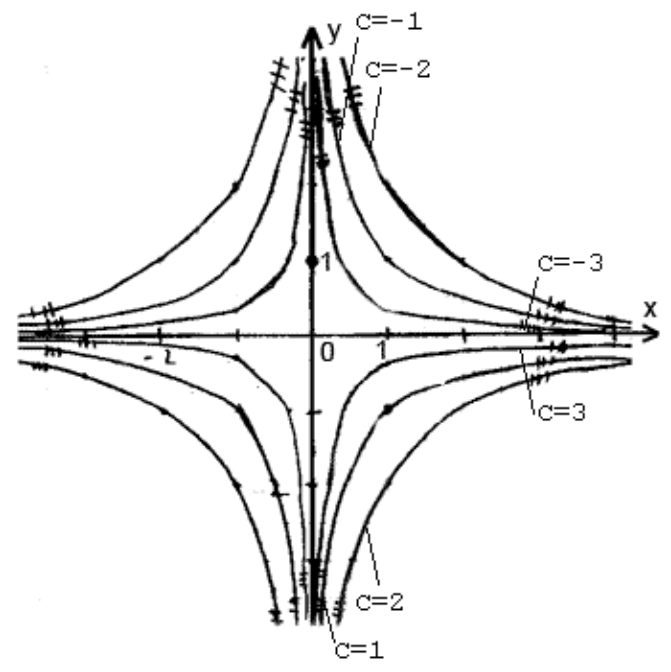
С геометрической точки зрения общее решение – это семейство кривых на координатной плоскости, а частное решение – это одна прямая этого семейства, проходящая через некоторую точку.
Давайте рассмотрим примеры решения некоторых ДУ. Начнем с ДУ первого порядка с разделяющимися переменными:
Здесь все очень просто как на уроке физкультуры, когда ученики класса делятся на две команды, в одну из которых входят только мальчики, а в другую – только девочки. Применительно к уравнению делаем следующее: в левую часть от знака равенства переносим все то, что содержит переменную y, а в правую часть – переменную x.
Получаем:
Далее интегрируем обе части:
Итоговое общее решение выглядит следующим образом: y = C(x-1) — 2. Все оказалось очень просто, не правда ли?
Не сложнее и решение однородных ДУ второго порядка с постоянными коэффициентами. Здесь всего-то и нужно знать из курса школьной алгебры, как решаются квадратные уравнения, а из курса по ДУ, как правильно записать общее решение.
Для наглядности рассмотрим пример:
Составляем характеристическое уравнение, заменяя переменную y на переменную k, а количество штрихов соответствующей степенью (два штриха – степень 2, один штрих – степень 1, нет штрихов – степень 0). Получаем квадратное уравнение, решить которое можно с помощью дискриминанта или теоремы Виета:
После того, как корни характеристического уравнения найдены, вспоминаем правила записи общего решения однородного ДУ:
- Корни характеристического уравнения являются действительными и различными. Общее решение записывается в виде:
- Корни характеристического уравнения являются комплексными. Общее решение записывается в виде:
- Корни характеристического уравнения являются действительными и равными. Общее решение записывается в виде:
Вспоминаем, что наше уравнение имеет два различных действительных корня. Следовательно, общее решение запишем в виде:
Решение линейных неоднородных ДУ с постоянными коэффициентами выполняется в два этапа:
- нахождение общего решения линейного однородного ДУ;
- нахождение и частного решения линейного неоднородного ДУ.
Выполнение первого этапа рассмотрено на примере чуть раньше. То, в каком виде мы будем искать частное решение неоднородного ДУ, зависит от того, что стоит в уравнении справа от знака равенства. Все возможные случаи подробно рассматривают в учебной литературе.
Итак, тема «Решение задач по дифференциальным уравнениям» изучается в ВУЗах, но, как было показано выше, решить некоторые ДУ может и школьник.
Дифференциальные уравнения и методы их решения рассматриваются практически в каждом учебнике по высшей математике и математическому анализу. Особенно хорошо данная тема рассмотрена в учебнике автора Пискунов Н.С., а называется он «Дифференциальное и интегральное исчисления: Учеб. Для втузов. В 2-х т. Т. II». С помощью данного учебника можно самостоятельно изучить методы решения тех типов ДУ, которые не были рассмотрены в данной статье.
Решение дифференциальных уравнений на заказ
У нас вы можете выгодно заказать решение задач с дифференциальными уравнениями. Нами накоплен большой опыт решения заданий по данной дисциплине, которым мы готовы поделиться с вами. Работа будет оформлена очень подробно. При заказе большого количества задач действует скидка. Купить решение можно, сделав заказ у нас на сайте.
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y»’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
Линейные дифференциальные уравнения в частных производных первого порядка
Линейные однородные уравнения в частных производных первого порядка
Пусть X 1 , X 2 , . Xn – заданные функции переменных x 1 , x 2 , . xn .
Чтобы решить линейное однородное уравнение в частных производных первого порядка:
необходимо решить систему обыкновенных дифференциальных уравнений (уравнение характеристик):
:
Далее нужно представить решение в виде:
φ 1( x 1 , x 2 , . xn ) = C 1 ,
φ 2( x 1 , x 2 , . xn ) = C 2 ,
.
φn- 1 ( x 1 , x 2 , . xn ) = Cn- 1 ,
где Ck – постоянные.
После чего сразу получаем общее решение:
,
где F – произвольная функция от n – 1 аргументов.
Если нужно получить частное решение с определенными граничными условиями, то необходимо подставить значения переменных из граничных условий в общее решение и найти вид функции F .
Линейные неоднородные уравнения в частных производных первого порядка
Пусть X 1 , X 2 , . Xn+ 1 – заданные функции от переменных x 1 , x 2 , . xn и z .
Чтобы решить линейное неоднородное уравнение в частных производных первого порядка:
,
необходимо решить уравнение характеристик:
.
Решение этой системы нужно представить в следующем виде:
φ 1( x 1 , x 2 , . xn , z ) = C 1 ,
φ 2( x 1 , x 2 , . xn , z ) = C 2 ,
.
φn ( x 1 , x 2 , . xn , z ) = Cn .
После чего сразу получаем общий интеграл в неявном виде:
где F – произвольная функция. Также общий интеграл можно представить в различных вариантах, например:
φ 1 = F ( φ 2 , φ 3 , . φn ) ,
φ 2 = F ( φ 1 , φ 3 , . φn ) ,
и т. д.
Примеры решений линейных уравнений в частных производных первого порядка
Однородное уравнение
Найти общее решение линейного однородного уравнения в частных производных первого порядка и решить задачу Коши с указанным граничным условием:
,
при .
Это линейное однородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
Это уравнение характеристик содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье будет выполнено автоматически.
Выбираем и решаем первое уравнение:
Здесь переменные уже разделены, интегрируем:
Интегралы табличные,
Потенцируем:
Отсюда
Подставим во второе уравнение:
Или:
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Умножим на x -1 и преобразуем:
Интегрируем:
Подставим полученное ранее выражение C1 = x y 2 :
Итак, мы нашли два интеграла уравнения характеристик:
Общее решение исходного уравнения в частных производных имеет вид:
где F — произвольная функция от двух аргументов F(φ1, φ2) . Найдем ее вид из граничного условия
при .
Рассматриваем решение на границе.
Положим x y = –1 :
Отсюда
На границе
.
Итак, мы нашли, что на границе функция F имеет вид:
F ( φ 1 , φ 2 ) = φ 1 φ 2 .
Такой же вид она имеет и во всей области
Подставляя
;
,
получаем частное решение исходного уравнения в частных производных с заданным граничным условием:
Общее решение:
где F — произвольная функция от двух аргументов F ( φ 1 , φ 2 ) .
Неоднородное уравнение
Найти поверхность, удовлетворяющую данному уравнению
,
и проходящую через данную окружность x + y + z = 0 , x 2 + y 2 + z 2 = a 2 .
Это линейное неоднородное уравнение в частных производных первого порядка. Составляем уравнение характеристик:
Оно содержит три уравнения:
;
;
.
Нам нужно выбрать и решить любые два из них. Тогда третье удовлетворится автоматически. Выбираем первое и второе уравнения.
Решаем уравнение:
Умножаем на 2 z и интегрируем:
Интегралы табличные,
Потенцируем:
Отсюда
x = C 1 y
Подставим во второе уравнение:
Или:
Замечаем, что , тогда
Это линейное уравнение. Решаем с помощью интегрирующего множителя. Разделим на y 2 и преобразуем:
Интегрируем:
Подставим полученное ранее выражение и преобразуем:
Итак, мы нашли два интеграла уравнения характеристик:
Для удобства дальнейших вычислений заметим, что функция от постоянной также является постоянной. Поэтому запишем интегралы в виде:
Общий интеграл исходного уравнения в частных производных имеет вид:
F ( φ 1 , φ 2) = 0
Но, поскольку F — произвольная функция от двух аргументов, то общий интеграл можно записать также в виде:
φ 1 = F ( φ 2) ,
где F — произвольная функция от одного аргумента.
Найдем вид этой функции, рассматривая решение на границе.
На границе, x 2 + y 2 + z 2 = a 2 , .
Из уравнения x + y + z = 0 , z = – ( x + y ) . Подставим в x 2 + y 2 + z 2 = a 2 и преобразуем:
x 2 + y 2 + ( x + y ) 2 = a 2
x 2 + y 2 + x 2 + 2 xy + y 2 = a 2
2 x 2 + 2 xy + 2 y 2 = a 2
Разделив на y 2 , имеем
Итак, мы нашли, что на границе:
.
Подставим в выражение общего интеграла:
φ 1 = F ( φ 2)
.
Сделаем подстановку
:
.
Итак, мы нашли, что на границе функция F имеет вид:
.
Такой же вид она имеет и во всей области, тогда
.
Подставляем выражения для φ1 и φ2 :
.
Умножим на a 2 y 2 .
Автор: Олег Одинцов . Опубликовано: 23-09-2014
http://mathdf.com/dif/ru/
http://1cov-edu.ru/differentsialnye-uravneniya/chastnie_proizvodnie/