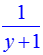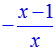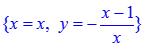Как решать уравнения в мэпл

Как решать уравнения в мэпл

Решение обыкновенных уравнений.

Для решения уравнений в Maple существует универсальная команда solve(eq,x) , где eq – уравнение, x – переменная, относительно которой уравнение надо разрешить. В результате выполнения этой команды в строке вывода появится выражение, которое является решением данного уравнения. Например:

Если уравнение имеет несколько решений, которые вам понадобятся для дальнейших расчетов, то команде solve следует присвоить какое-нибудь имя name . Обращение к какому-либо k –ому решению данного уравнения производится указанием его имени с номером решения k в квадратных скобках: name[k] . Например:

Решение систем уравнений.

Системы уравнений решаются с помощью такой же команды solve(,) , только теперь в параметрах команды следует указывать в первых фигурных скобках через запятую уравнения, а во вторых фигурных скобках перечисляются через запятую переменные, относительно которых требуется решить систему. Если вам будет необходимо для дальнейших вычислений использовать полученные решения уравнений, то команде solve следует присвоить какое-нибудь имя name . Затем выполняется присвоения команда assign(name) . После этого над решениями можно будет производить математические операции. Например:

Численное решение уравнений.

Для численного решения уравнений, в тех случаях, когда трансцендентные уравнения не имеют аналитических решений, используется специальная команда fsolve(eq,x) , параметры которой такие же, как и команды solve . Например:

Решение рекуррентных и функциональных уравнений.

Команда rsolve(eq,f) позволяет решить рекуррентное уравнение eq для целой функции f . Можно задать некоторое начальное условие для функции f(n) , тогда получиться частное решение данного рекуррентного уравнения. Например:

Универсальная команда solve позволяет решать функциональные уравнения, например:

F := proc ( x ) RootOf(_ Z ^2 — 3*_ Z + 2* x ) end

В результате получается решение в неявном виде. Однако Maple может работать с такими решениями. Неявное решение функционального уравнения можно попытаться преобразовать в какую-либо элементарную функцию с помощью команды convert . Продолжая приведенный выше пример, можно получить решение в явном виде:

Решение тригонометрических уравнений.

Команда solve , примененная для решения тригонометрического уравнения, выдает только главные решения, то есть решения в интервале [0,2 p ]. Для того, чтобы получить все решения, следует предварительно ввести дополнительную команду _EnvAllSolutions:=true. Например:

В Maple символ _ Z

обозначает константу целого типа, поэтому решение данного уравнения в привычной форме имеет вид , где n – целые числа.

Решение трансцендентных уравнений.

При решении трансцендентных уравнений для получения решения в явном виде перед командой solve следует ввести дополнительную команду _EnvExplicit:=true . Пример решения сложной системы трансцендентных уравнений и упрощения вида решений:

Решение уравнений

Методы нахождения корней полиномов, решения уравнений, содержащих элементарные и специальные функции и систем сложных уравнений

Уравнения с одной переменной

Для решения таких уравнений в Maple предусмотрены две команды: solve для символьного решения и fsolve для решения с ответом в численном виде. Например, формула для квадратного уравнения:

Синтаксис solve выглядит так: solve(equation,variable) . Параметры записаны через запятую. Если задать численные коэффициенты, то система попытается дать численные ответы:

Maple знает формулы для кубического уравнения:

но они сложны, неприятны по внешнему виду, и их почти никогда не применяют.

Используем численные коэффициенты, чтобы ответ был численным:

Этот результат – правильный, но поскольку Maple «думает» символами, то они не выглядят слишком пригодными. Для получения чисел с плавающей запятой следует применять уже известную команду evalf :

или вводить коэффициенты уравнения с десятичной точкой:

Команда solve с полиномами работает по-умному: она знает фундаментальную теорему алгебры о том, что полином n-го порядка имеет n корней. Например, если спросить о корнях уравнения x 6 + 1:

в ответе должны быть все шесть.

RootOf часто встречается при решении уравнений в Maple. В этой задаче задается полином с целыми коэффициентами, что для Maple означает попытку решить уравнение в радикалах (квадратных, кубических корнях и т. п.). Это создает проблему, и в результате он не может дать в решение ничего иного, кроме корня –1. Но если нужны только числа, либо используйте evalf , либо изменяйте коэффициенты на числа с плавающей точкой, и вы получите все шесть корней:

Maple может решать более сложные уравнения вроде cos(x) – x/10:

Снова RootOf , поэтому такой же подход к решению: чтобы получить хотя бы один корень, замените 10 на 10. или используйте evalf(s7)

При решении сложных уравнений надо проявлять осторожность, поскольку возможно более одного ответа, и Maple не даст все. Попробуем нарисовать функцию cos(x) – x/10 и увидим, как много у нее нулей, т. е. столько корней придется искать.

Maple на самом деле не обманывает: 1.427551779 есть решение, но не все.

Важно: прежде чем искать решение, постройте график, тогда будете знать, сколько корней надо найти.

Как заставить Maple выдать все корни? Поскольку они ищутся численно, применяется команда fsolve , которой надо задать уравнение, переменную и диапазон значений для поиска корней. Например, на рисунке видно, что корни находятся вблизи –9.6, –9.2, –4, –2, 1.5, 5 и 7. Это надо указать в fsolve , задавая диапазон поиска решений (x1..x2):

Посмотрите, что произойдет, если указать диапазон, где нет корней:

По общему правилу, когда Maple без вычислений возвращает то, что ему задали, это означает, что либо он не может найти ответ, либо вы ошиблись. Ищите, где ошибка.

Учтите, что вместо диапазона можно просто задать одно угаданное решение:

Здесь надо быть осторожным. Если для fsolve подсказано начальное значение, причем оно расположено близко к максимуму функции, нули которой ищутся, то fsolve может ошибиться или может найти решение не в том месте, где начальная подсказка. Посмотрим на примере метода секущих, почему так происходит:

Еще один способ контроля за решениями – опция avoid в fsolve .

Ищем решения уравнения cos(x) + x/3. Чтобы узнать, где искать корни, нарисуем функцию и увидим рядом с 3 два близко расположенных корня. Команда найдет один из них:

а вам нужен второй, и возникает проблема: как указать команде на него или как задать начальное значение. Можно так: ищи один корень вблизи 3, но не ищи s1:

Найдите все действительные или комплексные корни следующих полиномов. Используйте для этого команды solve и fsolve .

solve дает комплексные величины, а fsolve – нет. Это можно исправить, указав fsolve , что нужно искать комплексные решения: fsolve(x^2+1=0, x,complex) .

Посмотрите, что случается при использовании команды factor(f,complex) , где f – полином, который надо разложить.

(a) Найдите все решения уравнения e x = 10sin(x) между –5 и 20.

(b) Найдите все решения уравнения e (–x) = x, используйте solve и fsolve и сравните ответы.

(с) Найдите все корни функции для x между 0 и 10.

(d) Найдите все корни производной функции Бесселя между 0 и 100 и занесите их в вектор-столбец a n .

Эту задачу можно решить очень компактно с помощью команды seq с командой fsolve внутри нее.

Решение разбейте на части:

Шаг 1. Нарисуйте функцию между 0 и 100, затем несколько раз обновите диапазон графика, чтобы узнать, где первый и второй корни и как далеко они друг от друга (вы обнаружите, что они на расстоянии порядка π).

Шаг 2. Чтобы применить полученную информацию, используйте команду seq , чтобы генерировать все корни.

Команда seq , вроде такой: seq(n^2,n=0..20) , генерирует список чисел; затем учтите, что первый аргумент seq , который генерирует зависящее от n число, может быть чем угодно, даже результатом fsolve .

Вот пример построения последовательности нулей косинуса с помощью seq и fsolve , который основан на догадке, что начинать надо с 1.4 и расстояние между нулями π: seq(fsolve(cos(x)=0,x=1.4+n*Pi),n=0..20);

Шаг 3. Все, что вам теперь нужно сделать, – загрузить эти числа в вектор-столбец. Если команда seq не дала первый корень при x=0 , догадайтесь, как это сделать вручную.

Maple. Решение алгебраических задач. Решения уравнений, систем уравнений и неравенств в Maple

Страницы работы

Содержание работы

Решение алгебраических задач

Решение уравнений (часть 1)

Для решения уравнений, систем уравнений и неравенств в Maple используется команда (оператор) «solve». Например, для решения уравнения х2 – 6х + 5 = 0 набираем: > solve(x^2–6*x+5=0); 1, 5 Обратите внимание, что если аргумент solve не является уравнением (или неравенством), то Maple трактует его так, как если бы это выражение было приравнено к 0. Можно было бы написать «> solve(x^2–6*x+5);». При решении алгебраических уравнений Maple приводит все корни, включая комплексные: > solve(x^4=1); 1, –1, I, –I

Решение уравнений (часть 2)

С помощью команды «solve» можно решать не только алгебраические уравнения. Например, решим тригоно-метрическое уравнение tg x – 2 sin x = 0: > solve(tan(x)–2*sin(x)); Обратите внимание, что Maple привёл решения, лежащие в пределах одного промежутка периодичности (от –π до π). Для вывода всех решений необходимо присвоить зарезервированной переменной _EnvAllSolutions значение true: > _EnvAllSolutions := true; > solve(tan(x)–2*sin(x)); где _Z

обозначает любое целое число.

Решение уравнений (часть 3)

Приведём примеры применения функции «solve» для решения уравнений с несколькими переменными. Решим, например, уравнение xy + x – 1 = 0 относительно x: > solve(x*y+x–1,x); относительно y: > solve(x*y+x–1,у); В общем виде Maple решает это уравнение так: > solve(x*y+x–1); Видно, что форма ответа определяется вторым параметром (или его отсутствием) команды «solve», указывающим, относительно какой переменной решать уравнение.

Неравенства решаются тем же оператором «solve». Например, решим неравенство x2(x – 1) solve(x^2*(x–1) solve(x^2*(x–1)>=0); 0, RealRange(1, ∞) В переводе на математический язык ответ: <0>U[1; ∞). Открытый интервал (или луч) задаётся в Maple с помощью функции «Open», применяемой к концам интервала, задаваемого функцией «RealRange».

Решение системы уравнений

Все уравнения системы записываются в фигурных скобках через запятую. Решим например систему > solve(<3*x–2*y=10, x^2–y^2=15>); , Решим систему с параметром > solve(,);