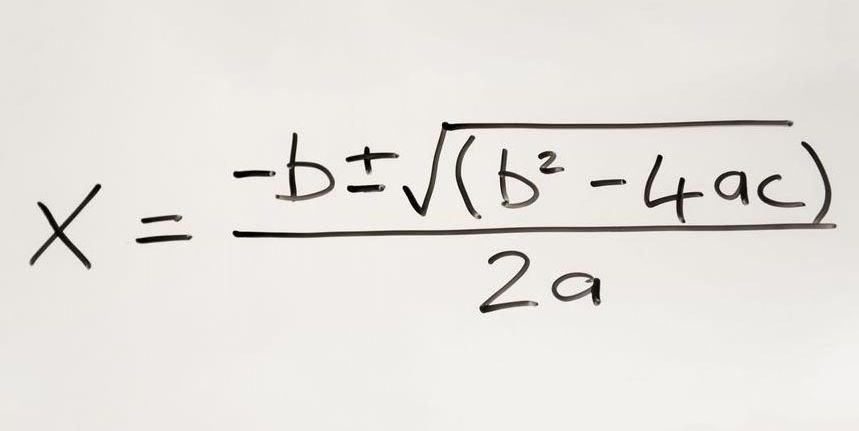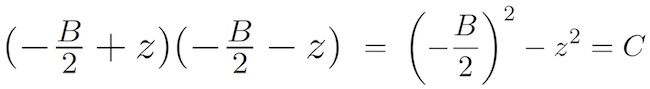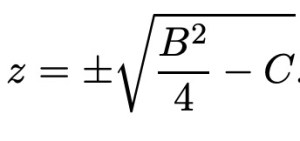Самый простой способ решения квадратичных уравнений упускается из виду в течение 4000 лет
Профессор математики открыл новый способ решения квадратных уравнений. Это вычислительно эффективнее и проще для запоминания, чем традиционная квадратичная формула. Удивительно, что такой простой метод оставался незамеченным в течение 4000 лет.
В элементарной алгебре квадратные уравнения могут быть решены с использованием различных методов, таких как факторинг, построение графиков, построение квадратов и другие.
История квадратичной формулы — формула обеспечивает решение (я) квадратного уравнения — может быть прослежена до древне-вавилонского периода около 2000–1600 гг. До н.э. Многие великие математики оставили свой след на этом предмете, и формула стала одной из самых важных частей в алгебре.
Формула, однако, довольно сложна, и ее вычисления несколько запутаны. Это может быть сложной задачей для начинающих изучающих алгебру.
Недавно математик из Университета Карнеги-Меллона в Питтсбурге опубликовал более простое решение для любого квадратного уравнения. Этот новый метод прост в запоминании и эффективен в вычислительном отношении.
По словам его автора, По-Шен Ло , он имеет потенциал для демистификации квадратичной формулы для студентов во всем мире.
Альтернативный метод решения квадратичных задач
Самый первый шаг — посмотреть, можно ли разложить квадратное уравнение следующим образом:
Если факторизация возможна, то квадратичная функция равна нулю при X=R или X=S. Согласно традиционному методу, если сумма и произведение R и S равно -B и C соответственно, то
А вот теперь начинается поворот.
Два числа суммируют с -B именно тогда, когда их среднее значение равно -B / 2. Рассмотрим эти два числа в виде -B / 2 ± z, где z — неизвестная величина, а произведение этих чисел равно C.
Если z оказывается равным нулю, то мы разложим с R = S = (- B / 2), в противном случае,
Квадратный корень всегда существует (с учетом комплексных чисел), поэтому искомые R и S всегда существуют для любого квадратичного уравнения. Таким образом, исходные корни могут быть выражены как
А, это новая квадратичная формула; гораздо проще и легче запомнить, чем предыдущий.
Почему сейчас?
Новый метод интуитивно понятен и не требует запоминания формулы вообще. Однако, более интересный вопрос, почему никто не думал об этом раньше.
Автор исследовал 4000-летнюю историю по этой теме: он изучал различные подходы, построенные древними вавилонянами, греками, индийцами, арабами и китайцами, а также современными математиками, но не нашел ничего похожего на его метод.
По-Шен Ло считает, что это связано с тем, как традиционный метод доказывает, что квадратные уравнения имеют два корня. Обычно считается, что квадратное уравнение всегда имеет два корня, и эти корни имеют произведение C и -B.
Возможно, к тому времени, когда математика продвинулась до «приличного уровня», Вавилонская техника исчезла из недавней памяти, и люди нашли подход завершения квадрата достаточно хорошим, чтобы интегрироваться в основную учебную программу.
Теперь вопрос в том, как быстро и насколько широко он будет распространяться.
Новое в блогах
Методика преподавания, или поиграем в математику (как в школах США преподают математику).
Глава из книги Айрата Димиева «Классная Америка». Учителя из Татарстана, проработавшем шесть лет в школах США. Если кто наберётся терпения и прочитает эту книгу до конца, то поймёт, что Михаил Задорнов со своими выпадами в адрес американцев отдыхает, нервно куря в углу.
Эта глава будет больше интересна учителям и отчасти родителям, задумывающимся об образовании их чад. Если вы все же наберетесь терпения и прочитаете её до конца, то будете иметь более-менее полное представление о том, чем американцы занимаются в школе.
Моя собственная дочь по прибытии в Америку пошла в седьмой класс в Johnston Middle School. Это одна из лучших школ. А по математике она была определена в так называемый Advanced Placement (сокращенно АР) класс. Считается, что АР классы для одаренных и увлеченных детей, где предмет преподается по более углубленной программе, нежели в обычном классе. Я очень внимательно следил за её учебной программой. Так вот, то, чем они занимались на уроке математики, было таким примитивом, что я даже не стану утомлять читателя подробностями. Это примерно уровень третьего-четвертого класса российской школы. И это в сильном классе. А что же там делается в обычных?
Более-менее нормальная математика начинается в восьмом классе. Я не оговорился — не алгебра и геометрия, а именно математика, так как никакой алгеброй там ещё не пахнет. Одна из моих российских коллег — Катерина — как раз ведет математику в восьмом классе в Fondren Middle School. По её словам я могу достаточно объективно судить о том, что там делается.
Год начинается с изучения отрицательных чисел, и решаются примеры на уровне:
Причем сидят ученики на этом очень долго, так как их воображение отказывается воспринимать отрицательные числа. Как говорит сама Катя, у них нет чувства чисел. Наиболее сложное для них — вычесть отрицательное число:
Решая последний пример, они получают либо 2, либо –2, но только не –8.
Следующий этап — уравнения. Самые простейшие, типа
Что интересно, они решают такие уравнения не так, как в России. Я сам неоднократно наблюдал это. Мы, чтобы найти х, делим 100 на 25, что кажется нам вполне логичным. Ведь х в 25 раз меньше, чем 100. Американцы делают это гораздо круче. Чтобы найти х, они делят обе части уравнения на 25. В результате слева остается х, а справа 4.
Круто, правда? Это может показаться очень грамотным с математической точки зрения, но совершенно не способствует пониманию учениками сути производимых действий. Они не успевают осознать, что х в 25 раз меньше 100, механически выполняя показанные учителем операции.
Следующий этап — проценты. Около месяца восьмиклассники учатся рассчитывать, сколько процентов составляет, например, 15 от 60. Причем опять-таки делают это чисто механически. Они не делят 15 на 60, чтобы осознать, что 15 составляет одну четверть от 60. Большинство из них и поделить-то это не могут без калькулятора. Просто механически выполняют операции по данному учителем шаблону.
Будучи практически ориентированными, на математике они учатся строить разные графики. Нет, не функции, которые даются не ранее девятого класса. Просто учатся откладывать точки с экспериментальными данными на оси координат. Наиболее сложным является построение так называемого Circle Graph — круга, где процентное содержание составляющих компонент представлено в виде сегментов. Для выполнения этого задания им нужно рассчитать, сколько градусов будет каждый сегмент, путем умножения процентной доли на 360 градусов. Несмотря на очевидную простоту, далеко не все восьмиклассники справляются с этим заданием.
Вся вышеперечисленная программа рассчитана на полгода. Апофеозом этого курса является решение следующего уравнения:
5 (х + 3) – 7 = 3х + 12
Но это, по словам Кати, уже является для них высшим пилотажем, и справляются с этим заданием не более 10 процентов её учеников.
По словам другого нашего общего коллеги — Камиля Сафина, преподающего математику в Fonville Middle School, ни один из его учеников даже при наличии в руках калькулятора не способен ответить на вопрос — сколько яблок можно купить на восемь долларов, если стоимость одного яблока 1 доллар 53 цента. Если бы одно яблоко стоило два доллара, то есть цифры делились без остатка, то ученики знали бы ответ. А вот реальный вопрос с реальными цифрами вводит их в полнейший ступор.
Закончив таким образом обучение в Middle School, ученики переходят в High School, где ещё раз выясняется, что математики они не знают.
Могу поклясться чем угодно, что более половины моих учеников в девятом классе Westbury High School не могли выполнить простейшее действие типа
Что касается математики, то программа High School не сильно отличается от программы Middle School. Теоретически самым верхом в обязательной программе по математике являются логарифмы и решение квадратных уравнений. На практике же большинство школ и учителей либо полностью отказываются от логарифмов, либо просто формально объясняют, что это такое.
Когда я в конце учебного года спросил своих учеников одиннадцатого класса, чему равен десятичный логарифм ста, то лишь двое из восьмидесяти опрошенных дали правильный ответ. Это при том, что вопросу предшествовало краткое объяснение, что такое логарифм.
Научиться решать квадратные уравнения среди учеников обычных классов могут процентов 10—20. Как я уже упоминал ранее, таких предметов, как тригонометрия или дифференциальное исчисление, в обязательной программе не предусмотрено совсем.
Однако главное даже не в том, что американские ученики проходят, а в том, что они усваивают. Более половины учеников обычных классов не могут справиться даже с элементарными математическими заданиями, несмотря на то что проходили это неоднократно, начиная с класса шестого и кончая одиннадцатым. А это уже говорит о том, что дело здесь не только и не столько в программе, сколько в методике и методологии обучения.
Основной целью обучения на уровне начальной и средней школы не является выработка каких-либо навыков и умения мыслить. Задача — дать общее представление о материале, суть которого сразу же; после; написания контрольной работы благополучно забывается. Вместо скучного логического мышления ученикам даются игровые шаблоны-схемы, с помощью которых они должны решать те или иные примеры и задачи. Никакого понимания производимых действий при этом нет. Впоследствии для решения другого типа задач им даются другие шаблоны. Эти шаблоны наслаиваются один на другой. В результате в головах обучаемых невообразимая каша, представляющая собой какую-то смесь обрывочных знаний и отдельных кусков всех этих схем-шаблонов.
Например, каждый американский ученик с начальной школы знает поговорку Please Excuse My Dear Aunt Sally. Этот шаблон подсказывает порядок выполнения математических операций. Первое слово please начинается на ту же букву, что и parentheses — «скобки». Это означает: в первую очередь нужно делать то, что в скобках. Далее следует степень, потом умножение, деление, сложение и вычитание. Зазубрил эту поговорку — и никакой тебе скучной логики. При этом они не понимают, что умножение и деление имеют ту же силу. Если они видят пример:
то сначала умножат 3 на 5, а потом разделят 6 на 15 и получат ответ 0,4 в строгом соответствии с шаблоном-поговоркой.
Думать же логически и разбираться в задаче они не приучены. Таких любимых нами в детстве задач, как «Из пункта А в пункт Б вышел поезд», в их учебной программе нет совсем. Я очень сомневаюсь, что даже американские ученики старших классов смогут решить такие задачи. Да им этого и не нужно.
Вместо логического мышления дети в школе обучаются играм и манипуляциям. Они на сравнительно короткий срок (как правило — до конца урока, в лучшем случае — до ближайшей контрольной) обучаются простым операциям-схемам, суть которых — что куда и как перенести или передвинуть. Вот, например, как их учат переводить метры в сантиметры.
Перед учениками шкала, на которой расположены приставки единиц измерения, начиная от меньших слева, заканчивая крупными справа: милли, санти, деци, один, дека, гекто, кило
Каждой единице соответствует ячейка. Таким образом, между метром и сантиметром две ячейки. Чтобы превратить, например, 5,372 метра в сантиметры, нужно перенести запятую на две ячейки. Теперь самое главное — нужно решить, в какую сторону переносить. Инструкция такова — все время переноси в сторону, обратную движению. По нашей шкале от метров к сантиметрам мы движемся справа налево, значит, запятую нужно перенести слева направо. Получаем 537,2 см. Осознать, что в метре 100 см и соответственно значение, выраженное в см, будет в сто раз больше, для них слишком сложно. Очень немногие могут понять это и использовать на практике.
Читатель мне не поверит, но большинство учеников 11-го класса постоянно путаются, переводя граммы в килограммы и наоборот. Если они перепутали, в какую сторону перенести запятую, то вполне могут написать:
34,5 г = 34500 кг
совершенно не смутившись полученным результатом.
Так они и переносят знаки слева направо и справа налево, не понимая смысла выполняемых операций. Учителя даже и не пытаются объяснить студентам, в чем их истинный смысл. Отчасти потому, что многие учителя в свое время сами обучались по подобным методикам.
Для лучшего усвоения материала учителей принуждают использовать «передовые методы обучения». Суть одного из них, на презентации которого мне пришлось побывать, заключается в том, что, совершая вышеописанное действие, ученики одновременно совершают физические движения. Они хлопают в ладоши, прыгают, трясут вытянутыми вверх руками и в одном случае (при делении), приседая, опускают вниз левую руку, а в другом — правую. Очень хорошо делать это все под музыку. Здорово? Здорово! Если бы не одно обстоятельство. Все это происходит не в детском саду и даже не в начальной школе. Такие методики навязываются на всевозможных тренингах учителям средней школы.
Рабочие тетради и работа в группах
Расскажу ещё об одном «гениальном» изобретении американской педагогической мысли. Кстати, эта заразная вещь в последние годы стала активно проникать в школы российские — родители, будьте начеку! Американские учителя, особенно гуманитарных и естественных наук, очень любят использовать так называемый worksheet, что в дословном переводе означает «рабочий листок». В России это называют рабочими тетрадями. Эти рабочие листки прилагаются как дидактический материал к любому изданию учебника. Для учителя они хороши тем, что не болит голова, какие составить вопросы и задачи — все уже продумано за него.
Рабочий листок разработан для каждого отдельного параграфа учебника и содержит от десяти до двадцати пунктов по теме каждого урока. Каждый пункт есть какое-либо утверждение, но в этих утверждениях пропущены отдельные ключевые слова или целые фразы. Ученики должны вписать пропущенные слова и фразы. Иногда дается утверждение и нужно ответить, верно утверждение или ложно.
По замыслу ученик, видимо, должен прочитать материал по учебнику, понять его, запомнить, а потом заполнить пробелы в рабочем листке. Американские студенты очень любят такую работу, особенно когда им разрешается выполнять эту работу в составе небольших групп. Я, будучи начинающим американским учителем, тоже иногда прибегал к этой форме обучения. Дал задание, и они его делают чуть ли не весь урюк.
Как-то моя дочь, учась в седьмом классе Johnston Middle School, принесла домой такой worksheet в качестве домашнего задания по, истории. Для выполнения этого задания ей предстояло прочесть в учебнике параграф объемом одиннадцать страниц. Это был только третий месяц её пребывания в Америке, английского языка до приезда в страну она не знала и на тот момент только-только начинала что-то понимать.
Задание было для нее невыполнимое, текст учебника оказался сложным даже для меня. Тем не менее я предложил ей поработать для начала самостоятельно, педагогично рассудив, что детей нужно приучать самостоятельно преодолевать трудности. Каково же было мое удивление, когда через часик она протянула мне практически полностью заполненный worksheet! Причем более половины задания было сделано правильно. Я задал ей пару наводящих вопросов, из чего мне стало понятно, что она по-прежнему почти ничего не понимает из текста. Тем не менее задание выполнено — листок заполнен!
В чем же дело? А в том, что предложения в рабочем листке идентичны с предложениями в тексте учебника. Необходимо только найти соответствующее предложение в учебнике и отыскать в нем пропущенное слово…
Нужно ли говорить, уважаемый читатель, что и американские ученики поступают совершенно так же, как это сделала моя дочь. За очень редким исключением они не понимают того, что написано в учебнике. (Вам кажется это утверждение абсолютно голословным? Тогда вот, пожалуйста, данные Национального центра образовательной статистики Америки. Согласно им 70% выпускников американских школ не понимают письменный текст средней сложности, другими словами — не понимают того, что читают. — Авт.)
Подавляющее большинство учеников не могут подобрать правильного слова, если предложение в рабочем листке сформулировано несколько иначе, чем в тексте. Причем в этом случае совершенно не важно, что вопрос очень простой и для ответа не нужно даже знать предмета, что это всего лишь здравый смысл. Многие из них не смогут написать, что вода — это жидкость, а кислород — газ, если не найдут идентичного предложения в тексте учебника. Но авторы учебника — люди понимающие, и потому тексты в рабочем листке и учебнике сходятся на 90 процентов.
Это ещё не все. Для пущей эффективности студенты могут заполнять эти рабочие листки не индивидуально, а в составе небольшой рабочей группы из трех-четырех человек. Американцы очень гордятся такой системой обучения (group work) и считают, что она гораздо эффективнее традиционной, где каждый выполняет свое задание в одиночку. Считается, что в группе обучаемые помогают друг другу усваивать материал. Они делятся мыслями, идеями, что-то друг другу подсказывают и пр. Согласен, в самой идее что-то есть. В определенных условиях такая методика может дать результат. Например, если мотивация обучаемых очень высока, то по такой системе можно предложить решать сложные многоступенчатые задачи. Также система хороша в выполнении лабораторных работ.
В условиях же обычной американской школы это совершенно не работает. Я заметил, что даже в моем самом продвинутом классе, где мотивация учащихся неимоверно высока, реально в работе участвуют один или двое членов группы — те, что быстрее соображают. Остальные просто не могут угнаться за ходом мыслей лидеров. В лучшем случае они успевают понять, как лидеры решили задачу. Но понять — ещё не значит научиться. Как известно, решенное другим человеком недолго задерживается в памяти.
В обычных же классах происходит следующее. Если ученики настроены работать, а учитель стоит над ними, то лидер выполняет задачу, а остальные просто бездумно списывают с него. В худшем же случае они болтают на посторонние темы, попутно что-то там пописывая на своих листочках. Читать написанное, как правило, нет никакого смысла.
Эта форма работы хороша тем, что в результате все справляются с заданием. Неважно, что один делал, а трое списывали, все четверо получают одинаковую хорошую оценку. Вот она, успеваемость, вот они, показатели! Вот оно, торжество американской системы образования, где every student can learn, every one can be successful.
Устный счет на калькуляторе
Ученики 11 и 12 классов, успешно закончившие курсы Algebra-1 и Algebra-2, не могут разделить десять в шестой степени на десять во второй. Причем они послушно зазубрили правило (чувствуется, что это вдалбливалось достаточно долго и упорно): «умножаем — складывай степени, делим — вычитай». Но вот произвести эти действия правильно могут единицы. Как вы думаете, что они делают, чтобы произвести эти вычисления? Догадались? Достают калькуляторы. Нет, они не набирают шесть нулей после единицы. Это продвинутые дети, и у них продвинутые калькуляторы, где есть кнопочка для работы с экспонентами! Они используют эту кнопочку и… все как один получают неправильный результат…
Оценить же полученный результат они не в состоянии. Могут, к примеру, поделить десять в третьей степени на десять во второй (то бишь тысячу на сто) и предъявить ответ: десять в пятой. То, что полученное число больше первоначального, их нисколько не смущает. К тому же многие из них просто не понимают, что десять в пятой степени — это сто тысяч, да и просто не в состоянии осознать величину этого числа. Многие не понимают, что тысяча — это десять сотен. И если большинство все же слышали, что миллион — это тысяча тысяч, то представить миллион как сто раз по десять тысяч способны лишь единицы.
Устный счет не развит совершенно. Любой набор цифр повергает их в шок.
Как-то в начале своей работы в американской школе на уроке химии в одиннадцатом классе показываю классу решение задачи на доске. После того как собственно химическая часть решения задачи закончилась путем постановки в формулу всех необходимых значений, получилась большая дробь: два числа в числителе, три в знаменателе, несколько экспонент.
Я предлагаю им самостоятельно завершить вычисления, справедливо полагая, что это уже дело техники, и ученики 11-го класса справятся с этим легко. Наивный! Бедные студенты растерянно смотрят на эту дробь, не зная, какую цифру первой ввести в калькулятор, и главное — как это сделать, ведь обычные цифры чередуются с экспонентами. Я им предлагаю решить это без калькулятора. По классу проходит смешок. Они думают, что учитель так нестандартно шутит.
Тогда я приступаю к решению и начинаю с сокращения чисел. Числа простые, специально подобранные для облегчения счета. Студенты понимают каждое мое отдельное действие и кивают головами. Более того, начинают подсказывать, что сократить на следующем этапе. Через какое-то время мы вместе с ними получаем ответ, и по классу прокатывается гул восторга. Они обалдело улыбаются и смотрят на меня как на факира. Дэвид Копперфилд отдыхает! Очевидно, за все одиннадцать лет учебы в школе ещё ни один учитель не показал им пример устного счета.
Это все происходит в моей образцово-показательной школе, где успевающие ученики. Они очень хотят понять, как это делается. Это прекрасные милые молодые люди с приятными лицами, и я искренне хочу научить их чему-нибудь. Поэтому начинаю им объяснять математику, хоть это и не моя работа. Прошу отложить в сторону калькуляторы и пытаюсь задействовать их логику — не работает. Бьюсь над этим минут десять, заходя к проблеме со всех сторон, — не доходит!
Тогда начинаю объяснять то же самое по американской схеме — большая половина класса тут же улавливает суть, и весь остаток урока нормально решает задачи. Но на следующий урок повторить то же самое могут уже лишь единицы. И это понятно — схема не может сидеть в голове долгое время.
Окружности Карлейля, или Как решать квадратные уравнения циркулем и линейкой
Томас Карлейль. Портрет работы Дэниэла Маклиса
Казалось бы, какая может быть связь между квадратными уравнениями и геометрическими инструментами — циркулем и линейкой? Однако эта связь есть, и ее исследование с разных сторон — увлекательнейшая задача, тесно связанная и с геометрией, и с алгеброй.
А при чем тут Томас Карлейль? Согласно Википедии, это британский писатель, публицист, историк и философ, автор многотомных сочинений «Французская революция» (1837), «Герои, почитание героев и героическое в истории» (1841), «История жизни Фридриха II Прусского» (1858–1865). О его занятиях математикой практически ничего не известно, и тем не менее, в честь него назван класс окружностей, помогающих решать квадратные уравнения.
А теперь — обо всем по порядку.
Что мы подразумеваем под решением уравнений циркулем и линейкой?
В школьных учебниках геометрии есть какие-то упоминания о возможности построения квадратичных иррациональностей с помощью геометрических инструментов, но в основном не в виде практических алгоритмов построения, а в качестве теоремы существования. Единственный школьный пример конкретного алгоритма, как-то связанного с квадратными уравнениями, — построение среднего геометрического. Давайте и мы тоже начнем с этой задачи.
Задача 1. Даны отрезки \(a\) и \(b\). Постройте отрезок, равный \(\sqrt
Решение. Отложим на одной прямой \(AD = a\), \(DB = b\). Построим окружность на отрезке \(AB\) как на диаметре. Восставим к нему перпендикуляр в точке \(D\) — в пересечении получим точку \(C\) (рис. 1). Тогда \(CD=\sqrt
Рис. 1. Построение среднего геометрического
Обычно после решения этой задачи в школе говорится, что поскольку мы умеем с помощью циркуля и линейки складывать, вычитать, также умножать и делить (пользуясь теоремой Фалеса), а вот теперь умеем и корни извлекать, то этого уже достаточно для того, чтобы по формулам для корней квадратного уравнения научиться строить отрезки соответствующей длины. Действительно, достаточно. Но ведь дико неудобно!
К счастью, есть и нормальный способ «геометрического» решения квадратных уравнений, известный вот уже более двух веков. Этот способ впервые был описан шотландским математиком и физиком Джоном Лесли в его книге «Элементы геометрии и плоской тригонометрии», изданной в 1809 году. В одном из последующих изданий Лесли добавил сноску о том, что идея этого способа принадлежит его бывшему ученику Томасу Карлейлю.
Рис. 2. Задача Лесли, страница из его книги
На рисунке 2, заимствованном из книги Лесли, сформулирована задача: «Построить прямоугольник, равновеликий данному прямоугольнику \(CDFE\), полупериметр которого равен данному отрезку \(BC\)». Ее решение, предложенное Карлейлем, показано на рисунке 3. Прокомментируем построение на этом рисунке. Вначале данный отрезок \(BC\) откладывается на продолжении меньшей стороны четырехугольника \((CE)\). Затем на большей его стороне откладывается \(CG=CE\), после чего с помощью параллельных прямых достраивается четвертая вершина прямоугольника \(ABCG\). Теперь достаточно построить окружность на диаметре \(AD\) — точки \(J\) и \(K\) ее пересечения с отрезком \(BC\) и дадут искомые стороны прямоугольника (\(BJ\) и \(JC\) или, как изображено на рисунке, \(BK\) и \(KC=KI\)).
Рис. 3. Задача Лесли в Википедии
Почему и как это работает? Проще всего ответить на этот вопрос с помощью системы координат. Поместим начало координат в точку \(C\), ось абсцисс направим влево (к \(B\)), а ось ординат вверх (к \(D\)). Кроме того, будем считать, что \(CE=e\), \(CB=b\), \(CD=d\). Тогда координатами точки \(A\) будут \((b;\ e)\), а значит, координатами \(M\) будут \((b/2;\ (d+e)/2)\). Это означает, что окружность с центром \(M\) и радиусом \(MG\ (=MA=MD)\) имеет уравнение
\[\left(x-\frac b2\right)^2+\left(y-\frac
\[x^2-bx+\left(\frac b2\right)^2+y^2-(d+e)y+\left(\frac
Теперь уже совсем нетрудно увидеть, что точки пересечения этой окружности с горизонтальной прямой \(BC\) (осью абсцисс) — это точки, для которых \(y=0\), а значит, они удовлетворяют уравнению
Как мы знаем из школьной алгебры (теорема Виета), сумма корней этого уравнения равна \(b\), а произведение равно \(de\). Таким образом, если \(K\ (x_1;\ 0)\) и \(J\ (x_2;\ 0)\), то \(CK=CJ=x_1+x_2=b=CB\), а \(CK\cdot CJ=x_1\cdot x_2=de\), т. е. площадь прямоугольника со сторонами \(CK\) и \(BK=CJ\) действительно равна площади исходного прямоугольника \(CDFE\).
То же самое можно было получить и не выписывая уравнения окружности, из чисто геометрических соображений. Ведь \(CK\cdot CJ\) — это произведение длины секущей на ее внешнюю часть, a \(de=CD\cdot CG\) — другое такое же произведение. По теореме о секущих, они равны, т. е. \(CK\cdot CJ=de\). А так как \(ABCD\) — прямоугольная трапеция, а \(M\) — середина ее боковой стороны, то высота в равнобедренном треугольнике \(MJK\) является одновременно средней линией трапеции и медианой в том же треугольнике. Отсюда сразу получаем, что \(CK=BJ\), а значит, \(CK+CJ=CB=b\).
Осмысление того, что способ Карлейля годится не только для одной этой задачи, пришло далеко не сразу. Сначала в 1867 году австрийский железнодорожный инженер Эдуард Лиль описал свой метод приближенного графического нахождения корней многочленов произвольной степени (см. в Википедии «Метод Лиля»). Но только еще через 58 лет (в 1925 году) американский профессор Джордж Абрам Миллер, занимавшийся историей математики в качестве хобби, объяснил связь между окружностью, использованной Карлейлем и Лесли, и применением метода Лиля к решению квадратного уравнения.
Способ Карлейля
Итак, пусть мы хотим решить приведенное квадратное уравнение \(x^2-sx+p=0\). Тогда мы должны взять на координатной плоскости точки \(A\ (0;\ 1)\) и \(B\ (s;\ p)\), найти середину \(C\) отрезка \(AB\) и построить окружность с центром в \(C\) и радиусом \(CA\) (рис. 4). Точки пересечения этой окружности с осью абсцисс и будут корнями уравнения.
Рис. 4. Окружность Карлейля — определение
Доказательство практически полностью повторяет решение задачи Лесли, приведенное выше.
Но мы, кажется, собирались что-то строить циркулем и линейкой? А здесь координатная плоскость. Ничего страшного! Все, что нам на самом деле нужно от координат, вполне сводится к двум осям. Действительно, вместо точки \(B\ (s;\ p)\) можно сразу рассмотреть ее проекции на оси \(B_1\ (s;\ 0)\) и \(B_2\ (0;\ p)\). Ведь если мы знаем коэффициенты \(a\) и \(p\), то построить именно эти точки на осях — проще простого. А дальше центр окружности получится пересечением серединных перпендикуляров к \(OB_1\) и \(AB_2\) (постарайтесь разобраться, почему это так, по рисунку 5).
Рис. 5. Окружность Карлейля — построение
Как видно из рисунка 5, способ с окружностью Карлейля не только простой, но и удивительно легкий для запоминания. Кроме начала координат, требуются всего три точки — \(B_1\) (абсцисса которой равна коэффициенту \(s\)) откладывается на оси абсцисс, а \(A\ (0;\ 1)\) и \(B_2\) (ордината которой равна \(p\)) — на оси ординат. Два серединных перпендикуляра, одна окружность — вуаля, корни готовы!
Как это применять?
Возможно, самое известное применение окружностей Карлейля — построение правильных многоугольников. Многие слышали о том, что построение правильного пятиугольника циркулем и линейкой возможно. (На самом деле — не только возможно, но было дано и полностью обосновано еще Евклидом.) Но многие ли пытались понять, как именно решается эта задача?
Задача 2. Дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный пятиугольник \(ABCDE\), вписанный в эту окружность.
Решение. Построение пятиугольника с помощью окружностей Карлейля отличается удивительной простотой. Начнем с координатных осей, проведя через центр круга прямую \(OX\), перпендикулярную \(OA\) (рис. 6). Радиус данной окружности будем считать равным 1. Теперь берем точку \(M\ (-1/2;\ 0)\) и строим окружность с центром \(M\), проходящую через \(X\). В пересечении с \(OA\) получаем точки \(H_1\) и \(H_2\). Если теперь в полученных точках построить единичные окружности, то они пересекут данную окружность как раз в точках \(B\), \(C\), \(D\), \(E\), являющихся вершинами правильного пятиугольника (на рисунке 6 он выделен красным, а единичные окружности — изображены синим пунктиром).
Рис. 6. Правильный пятиугольник
Почему это работает и при чем тут Карлейль? А вот при чем. Способ Карлейля утверждает, что построенная окружность с центром \(M\) находит корни квадратного уравнения для \(s;\ p)=(-1;\ -1)\), поскольку \(M\) — середина отрезка \(XY\), где координаты точки \(Y\) как раз и равны (\(-1;\ -1)\). Значит, \(H_1\) и \(H_2\) — корни квадратного уравнения \(x^2+x-1=0\). Это знаменитое уравнение золотого сечения. Для нас достаточно использовать его «тригонометрическую» ипостась.
Лемма. Корнями квадратного уравнения \(x^2+x=1\) являются величины \(2\cos72^<\circ>\) и \(2\cos144^<\circ>\).
Доказательство. Косинусы этих углов удовлетворяют тригонометрическому уравнению \(\cos3\alpha=\cos2\alpha\), при этом они отличны от корня \(\alpha=0\). Преобразование уравнения \(\cos3\alpha=\cos2\alpha\) в алгебраическое с помощью замены \(x=2\cos\alpha\) дает уравнение \((x-2)(x^2-x-1)=0\), что и требовалось доказать. (Корень \(x=2\) соответствует \(\alpha=0\).)
Итак, с помощью метода Карлейля и «золотой» леммы мы выяснили, что точки \(H_1\) и \(H_2\) имеют координаты \((2\cos144^<\circ>;\ 0)\) и \((2\cos72^<\circ>;\ 0)\) соответственно. А дальше мы в этих центрах построили единичные окружности, т. е. окружности того же радиуса, что и данная окружность с центром \(O\). Ясно, что они пересекут окружность \((O,\ A)\) на серединных перпендикулярах к отрезкам \(OH_1\) и \(OH_2\) соответственно. Осталось только понять, что серединные перпендикуляры — это прямые \(x=\cos72^<\circ>\) и \(x=\cos144^<\circ>\), а значит, точки \(B\), \(E\), \(C\) и \(D\) пересечения окружностей имеют координаты \((\cos72^<\circ>;\ \sin72^<\circ>)\), \((\cos72^<\circ>;\ -\sin72^<\circ>)\), \((\cos144^<\circ>;\ \sin144^<\circ>)\) и \((\cos144^<\circ>;\ -\sin144^<\circ>)\), т. е. углы \(AOB\) и \(AOE\) равны 72 градусам, а углы \(AOC\) и \(AOD\) — 144 градусам. А это и означает, что они являются вершинами правильного пятиугольника. Доказательство правильности построения на этом завершено.
О сложности построений и «геометрографии» Эмиля Лемуана
Француз Эмиль Мишель Гиацинт Лемуан по праву считается одним из отцов современной «геометрии треугольника». Вероятно, вы слышали о точке Лемуана в треугольнике или об окружностях Лемуана. Он же в 1892 году опубликовал работу «Геометрография, или искусство геометрических конструкций» («La Géométrographie ou l’art des constructions géométriques»), в которой впервые предложил сравнивать различные геометрические построения по количеству требуемых элементарных операций (а лучшим построением считать то, на которое тратится меньшее число операций). Оптимальным («геометрографическим») способом Лемуан называет самый экономный из известных алгоритмов построения.
Элементарных операций Лемуан насчитал пять:
\(S_1\) — приложить линейку к определенной точке;
\(S_2\) — провести прямую линию;
\(C_1\) — поставить ножку циркуля в определенную точку;
\(C_2\) — изменить радиус циркуля, поставив ножку с карандашом в определенную точку;
\(C_3\) — провести циркулем окружность.
При этом Лемуан считал циркуль устойчивым, т. е. после проведения окружности сохраняющим выставленный радиус. Таким образом, следующая окружность того же радиуса, по Лемуану, требует уже не трех операций: \(C_1+C_2+C_3\), а всего двух: \(C_1+C_3\).
Сосчитаем, например, количество операций в построении корней уравнения с помощью окружности Карлейля, показанном на рисунке 5. Оси координат и точки \(A\), \(B_1\) и \(B_2\) заданы. Построение серединного перпендикуляра к отрезку \(OB_1\) — это две окружности равных радиусов и одна прямая, т. е. \((2C_1+C_2+2C_3)+(2S_1+S_2)\). Следующий серединный перпендикуляр — это \((2C_1+2C_3)+(2S_1+S_2)\), потому что мы строим его, не меняя радиуса циркуля. Тем самым, мы построили центр, затратив 15 элементарных операций. И наконец, сама окружность Карлейля — это еще \(C_1+C_2+C_3\). Итого «сложность» построения \(5C_1+2C_2+5C_3+4S_1+2S_2\) равна 18.
Упражнение 1. Придумайте другой способ построения окружности Карлейля, имеющий сложность 17 или меньше.
Подсказка. Центр этой окружности — середина отрезка, одним из концов которого является \(B_1\). Постройте сначала второй конец этого отрезка.
Современная компьютерная игра-головоломка Euclidea (euclidea.xyz) также требует от решателей задач найти самое экономное построение, но, в отличие от Лемуана, не подсчитывает предварительные операции \(S_1\), \(C_1\) и \(C_2\), а считает только количество проведенных линий (т. е. \(S_2+C_3\) в терминологии Лемуана). С точки зрения Euclidea, построение окружности Карлейля имеет сложность 7.
Можно ли отыскать корни квадратного уравнения с меньшей сложностью?
Когда автор начинал писать эту статью, он предполагал, что этот вопрос будет повешен в качестве финальной улыбки Чеширского Кота и оставлен читателю для самостоятельного решения. Однако планы немножко поменялись, и сейчас я хочу показать более экономный способ, а читателям предложить обдумать, нельзя ли найти еще лучший.
Во-первых, откажемся от оси ординат. Зачем она нужна, если все корни мы ищем на оси абсцисс?
Пусть у нас есть всего одна ось, а на ней — четыре известные точки \(O\ (0)\), \(E\ (1)\), \(S\ (X+Y)\) и \(P\ (XY)\). Последние две точки соответствуют коэффициентам того уравнения, которое мы хотим решить. Рисунок 7 соответствует ситуации, когда \(0 Рис. 7. Четыре точки на одной оси
Вначале проведем две окружности равных радиусов с центрами в \(P\ (XY)\) и \(E\ (1)\) (рис. 8) — как будто мы хотим строить середину отрезка между этими точками. Радиус окружностей возьмем таким, чтобы первая окружность прошла через точку \(S\ (X+Y)\). Отметим \(C\) — общую точку этих окружностей.
Рис. 8. Начало построения
Затем построим еще две окружности — окружность с центром \(O\ (0)\), проходящую через \(C\), и окружность такого же радиуса с центром \(S\). Их точку пересечения (любую из двух точек) назовем \(D\) (рис. 9).
Рис. 9. Вторые две окружности
И (немного неожиданный, как и полагается улыбке Кота) финальный шаг — окружность с центром \(D\), радиус которой точно такой же, как у двух первых (рис. 10). Нетрудно убедиться, что в пересечении этой окружности с осью абсцисс получатся нужные корни уравнения. Так получается потому, что разность квадратов радиусов построенных окружностей равна \(XY\), и по теореме Пифагора квадрат длины отрезка между точками пересечения пятой окружности с прямой равен \((X+Y)^2-4XY=(X-Y)^2\). А поскольку середина этого отрезка имеет координату \((X+Y)/2\), то правый конец отрезка совпадает с большим из чисел \(X\), \(Y\), а левый — с меньшим.
Рис. 10. Корни уравнения найдены
Сосчитаем сложность: \(2C_1+C_2+2C_3\) на первую пару окружностей, столько же на вторую и еще \(C_1+C_2+2C_3\) на последнюю окружность — всего \(5+5+3=13\), вместо прежних 17 или 18. Ура!
Дополнение.
Построение правильного 17-угольника
Задача 3. Пусть дана окружность с центром \(O\) и точка \(A\) на ней. Постройте правильный 17-угольник с вершиной \(A\), вписанный в эту окружность.
Эта задача, в отличие от трех неразрешимых задач древности, стала знаменитой после того, как была решена 19-летним Карлом Фридрихом Гауссом. Биографы Гаусса пишут, что только после ее решения Гаусс окончательно выбрал своей будущей профессией математику, а не литературу. Известна также легенда, что Гаусс завещал выбить на своем могильном камне изображение правильного 17-угольника. Кажется, даже если такое завещание было, то оно оказалось невыполненным, а вот на памятнике Гауссу в Брауншвейге след его юношеской работы есть (рис. 11 и 12).
Рис. 11. Памятник Гауссу в Брауншвейге
Полное описание гауссова метода решения этой задачи, пожалуй, далеко выходит за рамки одной статьи, но набросок метода дать нетрудно. Правда, это потребует от читателя хорошего знакомства с комплексными числами.
Решение. Основной идеей Гаусса было циклическое упорядочение комплексных корней 17-й степени из 1 — такое, чтобы каждый следующий корень был определенной степенью предыдущего. Он доказал, что полный цикл получится тогда, когда эта определенная степень равна 3.
Далее Гаусс разбил этот цикл на два куска, которые он назвал периодами. В один период вошла половина корней — все корни на нечетных местах цикла, в другой — вторая половина:
Гаусс заметил, что сумма двух построенных им величин \(\eta_<02>+\eta_<12>\), равная сумме всех корней уравнения, равна \(-1\), а их произведение равно \(-4\). (Первое наблюдение Гаусса легко следует из теоремы Виета для уравнения \(x^<17>-1=0\), так как сумма всех корней вместе с корнем \(x=1\) равна 0. Второе же наблюдение несложно проверить непосредственным вычислением. Для этого достаточно просто перемножить выражения — каждое содержит по 8 слагаемых, в произведении их будет 64, и из соображений симметрии ясно, что каждая степень будет встречаться по 4 раза, поэтому произведение равно учетверенной сумме.) Иными словами, две эти величины — корни квадратного уравнения с известными коэффициентами.
Дальше — проще. Гаусс просто продолжает разбивать каждый период на два меньших:
Суммы значений \(\eta_<04>+\eta_<24>\) и \(\eta_<14>+\eta_<34>\) — уже известные нам величины \(\eta_<02>\) и \(\eta_<12>\), а их произведения равны \(-1\) (убедитесь в этом сами, раскрыв скобки в произведениях). Следовательно, мы снова знаем квадратные уравнения, корни которых нужно отыскать.
Следующим шагом точно так же вводятся периоды длины 2 — их всего восемь, от \(\eta_<08>\) до \(\eta_<78>\). Собственно, этот шаг уже является последним, потому что \(\eta_<08>=\tau^1+\tau^<16>=2\cos(\pi/17)\), так что, зная величину \(\eta_<08>\), мы легко построим вершины правильного 17-угольника, соседние с заданной вершиной \(A\) (аналогично построению вершин по точке \(H_2\) для правильного пятиугольника).
Рис. 12. Семнадцатиугольная звезда на памятнике
http://maxpark.com/community/3376/content/1615303
http://elementy.ru/nauchno-populyarnaya_biblioteka/436237/Okruzhnosti_Karleylya_ili_Kak_reshat_kvadratnye_uravneniya_tsirkulem_i_lineykoy