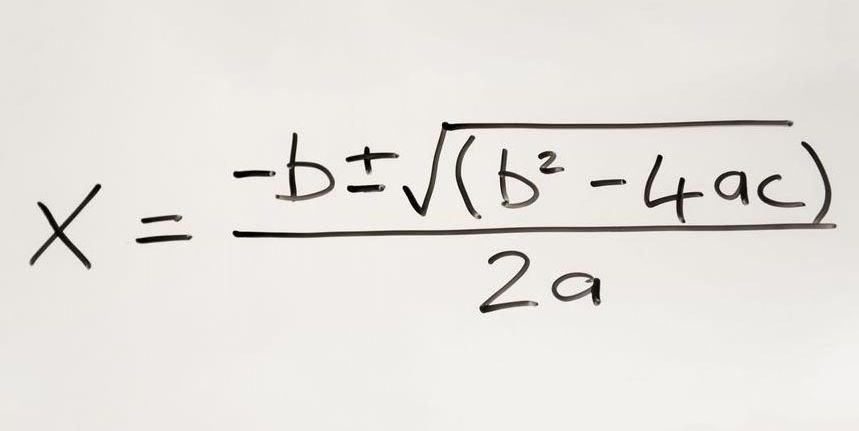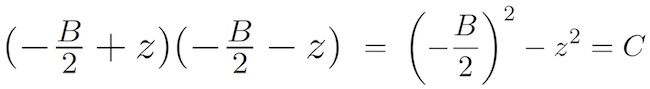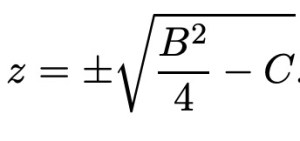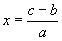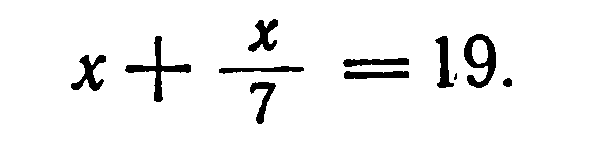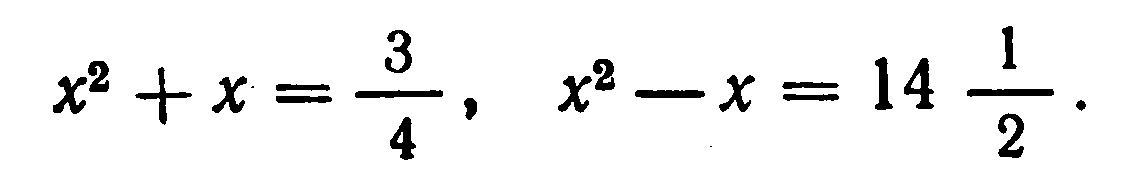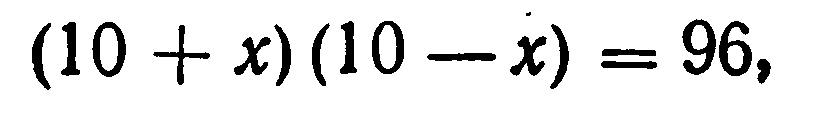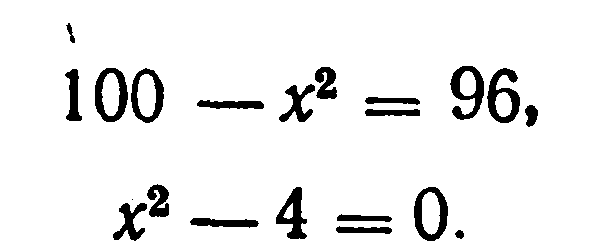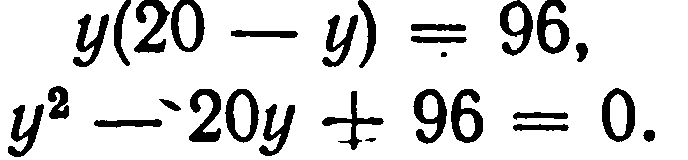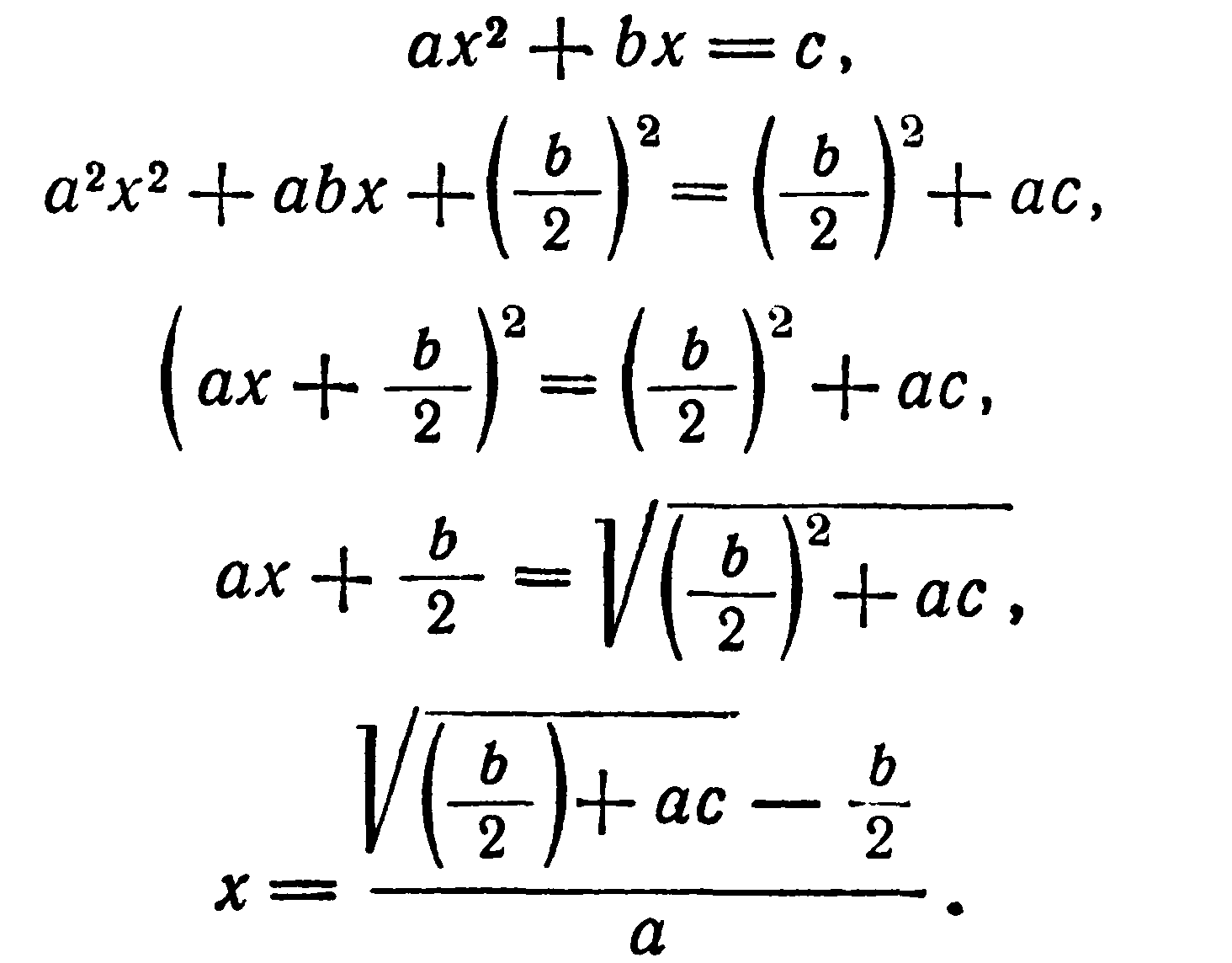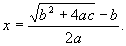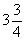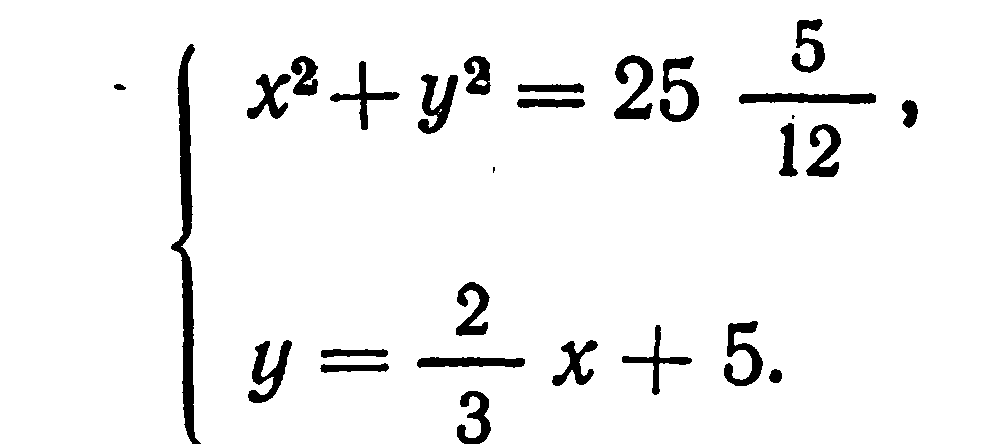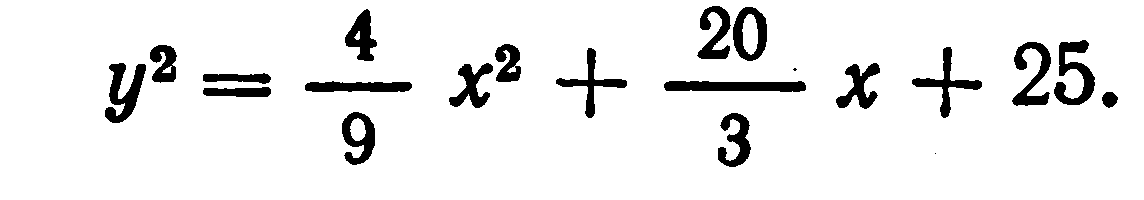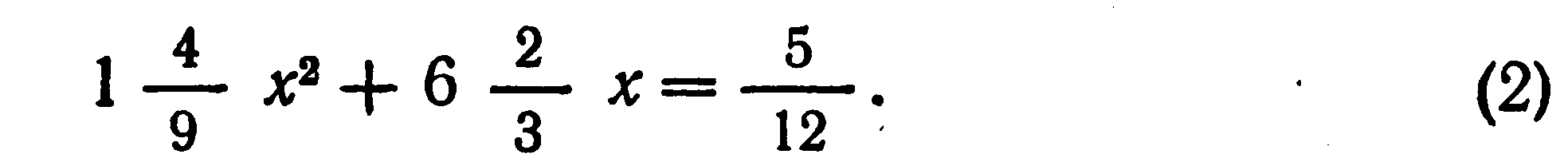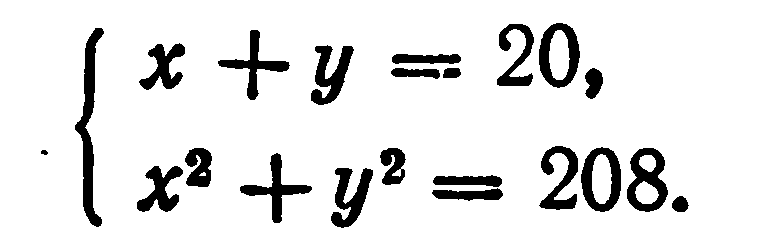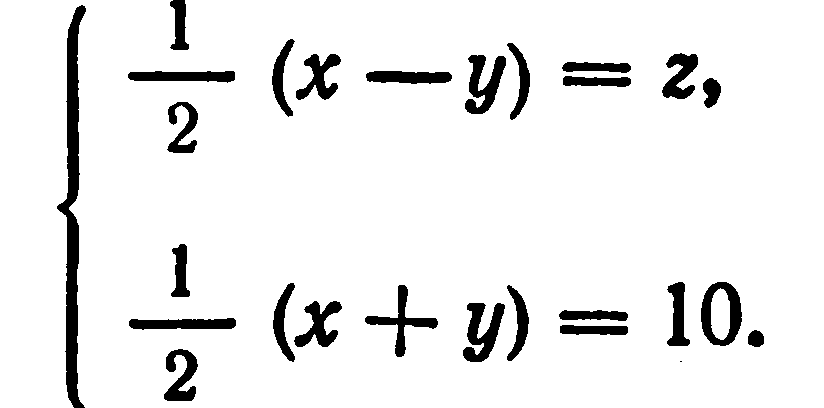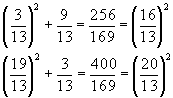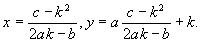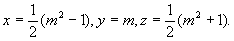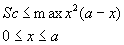Как решают уравнения в разных странах

Как преподают математику в разных странах

Система образования и манера преподавания отличаются в разных странах, но набор учебных дисциплин во всём мире плюс-минус одинаковый. В новой статье разбираем опыт зарубежных коллег и делимся любопытными приёмами преподавания математики.

Подход, объём занятий, оценка и результат обучения в виде математических знаний и умения применять их в реальной жизни за рубежом сильно отличаются от наших. Например, в большинстве стран математику традиционно преподают мужчины, где их больше половины, а в Японии — даже более 70 %. Только в России и Израиле свыше 90 % учителей математики — женщины.
Наши учителя тратят больше времени на подготовку к урокам, проверку домашних работ, общение с учениками и их родителями, то есть глубже погружены в профессию. И хотя российская математическая школа по-прежнему высоко котируется на мировом уровне, интересные идеи можно подсмотреть и у зарубежных преподавателей.

Как учат математике в Англии?

У британских школьников широкий математический кругозор. Дети идут в школу в 4 года и сразу начинают заниматься математикой. Чтобы им не было скучно, занятия проходят в игровой форме: малыши делят пиццу, раскладывают кубики Lego. К 6 они уже работают с дробями и знают, что половина, 50 %, ½ и даже угол 180 градусов — это одно и то же. Причём это не зазубренные термины, а основанное на практике понимание.

Математика прочно связана с реальной жизнью, и задания не кочуют из одного издания в другое с незапамятных времён, а адаптируются под нынешние реалии, то, с чем ребята сталкиваются ежедневно или столкнутся в ближайшем будущем. Это конвертация валют или бюджет на покупки. Основы геометрии подаются через дом, участок. Например, сколько краски потребуется, чтобы сделать ремонт.

Важный методический момент — цикличность обучения. Одни и те же темы повторяются от года к году, но каждый раз на более высоком уровне. Скажем, дроби с процентами есть как для пятилеток, так и в выпускном классе. Эта повторяемость помогает избежать пробелов и провалов в образовании, поскольку маленький ребёнок ещё не осознаёт, какие темы действительно важные и системообразующие.

Как учат математике в США?

При общности подходов — изучении тем по несколько лет на разных уровнях сложности, обилии практических задач — математическое образование в США отличается от британского. Американцы сильно продвинулись в плане стандартизации и формализации программы. В учебниках и пособиях есть абсолютно всё для успешной сдачи экзамена. Ситуация, когда на аттестации попадётся задание, которое не разобрано подробно в учебной программе, невозможна.

«Разжёвывается» материал максимально понятно и доступно, а сам курс шире и объёмнее российского, однако обширность приводит к поверхностности. Особенно это касается тех, кто выбрал обычную, а не углублённую программу по математике. Такие дети осваивают по всем темам только базовые, простейшие задания. Остальные учатся более интенсивно, участвуют в олимпиадах. Выбор ученики делают сами уже в шестом классе. Процесс обучения устроен неформально, дети много общаются с учителем и между собой, хорошо социализируются.

Активное использование калькулятора и других средств автоматизации зачастую приводит к отсутствию базовых навыков устного счёта, а впоследствии — к непониманию иррациональных чисел. Сложности возникают у американских школьников и с доказательством теорем, поскольку в геометрии упор также сделан на вычислительные задачи, а не на усвоение закономерностей. Если российскую методику обучения математике обычно критикуют за излишнюю академичность, но в США налицо другая крайность — недостаток академических знаний.

Как учат математику в Китае?

В китайских школах упор сделан на интерактивное обучение, в котором участвует весь класс — такие упражнения занимают три четверти всего урока. Объясняется всё в игровой форме и на основе междисциплинарных связей. Например, учитель может с помощью класса выиграть у компьютера партию в шашки на интерактивной доске, а затем показать географическую карту и объяснить, что координаты их города в виде пары чисел и вообще система GPS устроены по тому же принципу, что и ходы в игре. Упражнения по тригонометрии для ребят постарше помогают нарисовать логотип МакДоналдса, и подобных заданий в китайских школах много.

Преимущество интерактивного метода в ускорении процесса для каждого ученика. Учитель просит всех поднять карточки с ответом на вопрос или задачу. Если много ошибок, это позволяет сразу понять, что детям нужна помощь, и непонятный момент разбирают сразу всем классом. Если учитель видит, что кто-то всё равно отстал, то обязательно просит родителей позаниматься дополнительно дома и наверстать. При этом общий объём домашних работ снижается. В начальной школе ученики могут получить на дом задание программировать или играть на пианино.

Высокие требования предъявляют и к педагогам. Кроме того, в Китае сильнейшие учителя работают не с самыми талантливыми детьми, а с самыми слабыми и проблемными, что выравнивает общий уровень подготовки. Образование здесь — главный способ подняться по социальной лестнице. На уроках царит строгая дисциплина, всё расписано по минутам.

Как учат математике в Сингапуре?

Сингапур — для многих экзотическая страна, однако её экономика и образование за последние полвека совершили мощнейший скачок и потому достойны серьёзного изучения. Сингапурская система использует эвристический подход, идёт от частного к общему. Сначала дети решают много практических задач без теории, а потом, основываясь на личном опыте, делают выводы и обобщают.

Основная цель — совместная деятельность учителя и детей. Тему урока анонсирует не учитель — её выводят вместе через проблемные ситуации и диалог. Сингапурская система хорошо развивает коммуникабельность, критическое мышление и креативность, поскольку основана на командной работе и создании психологически комфортной, безопасной среды для учащихся.

Ученики сидят за столом по четыре человека, у каждого есть партнёр по лицу (тот, кто сидит напротив тебя) и партнёр по плечу (тот, что сидит рядом). Много работы в парах, где один из партнёров имитирует роль учителя — так дети учатся говорить, слушать и исправлять ошибки друг друга. При решении задач используют схемы и рисунки, не составляя уравнения. Сингапурские дети не отрабатывают вычисления на примерах — всё это изучают и осваивают через задачи. Большое внимание уделяется логике, которая у нас порой даётся сжато.

Несмотря на существенные различия в подходах — будь то либеральный американский, где детям предоставлено много свободы, или основанный на дисциплине китайский, — идеальной методики не существует. Однако черпая у коллег, в том числе и зарубежных, лучшее, мы быстрее приблизимся к этому идеалу.

А чтобы у вас оставалось время на новые идеи, воспользуйтесь базой «ЯКласс» — задания по математике, алгебре и геометрии доступны в разделе «Предметы».

Самый простой способ решения квадратичных уравнений упускается из виду в течение 4000 лет

Профессор математики открыл новый способ решения квадратных уравнений. Это вычислительно эффективнее и проще для запоминания, чем традиционная квадратичная формула. Удивительно, что такой простой метод оставался незамеченным в течение 4000 лет.

В элементарной алгебре квадратные уравнения могут быть решены с использованием различных методов, таких как факторинг, построение графиков, построение квадратов и другие.

История квадратичной формулы — формула обеспечивает решение (я) квадратного уравнения — может быть прослежена до древне-вавилонского периода около 2000–1600 гг. До н.э. Многие великие математики оставили свой след на этом предмете, и формула стала одной из самых важных частей в алгебре.

Формула, однако, довольно сложна, и ее вычисления несколько запутаны. Это может быть сложной задачей для начинающих изучающих алгебру.

Недавно математик из Университета Карнеги-Меллона в Питтсбурге опубликовал более простое решение для любого квадратного уравнения. Этот новый метод прост в запоминании и эффективен в вычислительном отношении.

По словам его автора, По-Шен Ло , он имеет потенциал для демистификации квадратичной формулы для студентов во всем мире.

Альтернативный метод решения квадратичных задач

Самый первый шаг — посмотреть, можно ли разложить квадратное уравнение следующим образом:

Если факторизация возможна, то квадратичная функция равна нулю при X=R или X=S. Согласно традиционному методу, если сумма и произведение R и S равно -B и C соответственно, то будет полным набором корней.

А вот теперь начинается поворот.

Два числа суммируют с -B именно тогда, когда их среднее значение равно -B / 2. Рассмотрим эти два числа в виде -B / 2 ± z, где z — неизвестная величина, а произведение этих чисел равно C.

Если z оказывается равным нулю, то мы разложим с R = S = (- B / 2), в противном случае,

Квадратный корень всегда существует (с учетом комплексных чисел), поэтому искомые R и S всегда существуют для любого квадратичного уравнения. Таким образом, исходные корни могут быть выражены как

А, это новая квадратичная формула; гораздо проще и легче запомнить, чем предыдущий.

Почему сейчас?

Новый метод интуитивно понятен и не требует запоминания формулы вообще. Однако, более интересный вопрос, почему никто не думал об этом раньше.

Автор исследовал 4000-летнюю историю по этой теме: он изучал различные подходы, построенные древними вавилонянами, греками, индийцами, арабами и китайцами, а также современными математиками, но не нашел ничего похожего на его метод.

По-Шен Ло считает, что это связано с тем, как традиционный метод доказывает, что квадратные уравнения имеют два корня. Обычно считается, что квадратное уравнение всегда имеет два корня, и эти корни имеют произведение C и -B.

Возможно, к тому времени, когда математика продвинулась до «приличного уровня», Вавилонская техника исчезла из недавней памяти, и люди нашли подход завершения квадрата достаточно хорошим, чтобы интегрироваться в основную учебную программу.

Теперь вопрос в том, как быстро и насколько широко он будет распространяться.

Методы решения уравнений в странах древнего мира

История алгебры уходит своими корнями в древние времена. Задачи, связанные с уравнениями, решались ещё в Древнем Египте и Вавилоне. Теория уравнений интересовала и интересует математиков всех времён и народов.

В Древнем Египте и Вавилоне использовался метод ложного положения (“фальфивое правило”)

Уравнение первой степени с одним неизвестным можно привести всегда к виду ах + Ь == с, в котором а, Ь, с — целые числа. По правилам арифметических действий ах = с — b,

Если Ь > с, то с — b число отрицательное. Отрицательные числа были египтянам и многим другим более поздним народам неизвестны (равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке).

Для решения задач, которые мы теперь решаем уравнениями первой степени, был изобретен метод ложного положения.

В папирусе Ахмеса 15 задач решается этим методом. Решение первой из них позволяет понять, как рассуждал автор.

Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали “хау” и переводили словом “куча” (“куча” или “неизвестное количество” единиц). Теперь читают немного менее неточно: “ага”.

bqt задача № 24 сборника Ахмеса:

“Куча. Ее седьмая часть (‘подразумевается: “дают в сумме”) 19. Найти кучу”.

Запись задачи нашими знаками:

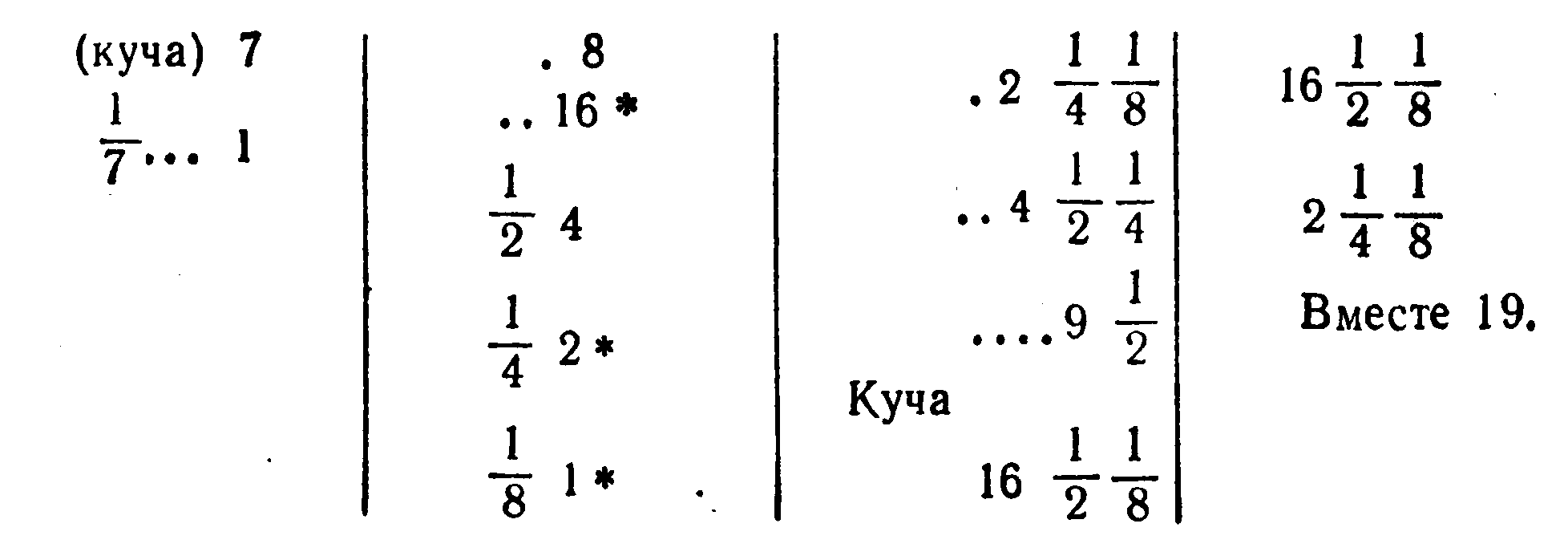
Решение Ахмеса может быть представлено в наших символах в следующих четырех столбцах:

Во многих задачах в начале или в конце встречаются слова: “Делай как делается”, другими словами: “Делай, как люди делают”.

Смысл решения Ахмеса легко понять.

Делается предположение, что. куча есть 7; тогда 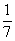ее часть есть 1. Это записано в первом столбце.

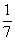
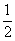
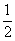
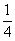
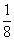
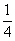
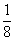
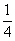
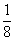
Во втором столбце записано, что при предположении х=7 куча и ее часть дали бы 8 вместо 19. Удвоение предположения дает 16. Автор, в уме очевидно, прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19. Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат; для получения в сумме 19 первоначальное предположение надо умножить -на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3. Ахмес находит от 8, получает 4. Так как это больше нехватки 3, то на предположение умножить нельзя. Но от 8 есть 2, от восьми 1. Ахмес видит, что и первоначального результата дают точно те 3 единицы, которых не хватало. Отметив и значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на

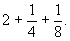
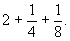
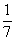
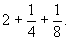
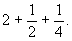
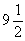
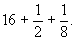
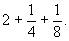
Умножение числа 7 на смешанное число Ахмес заменяет умножением смешанного числа на 7. В третьем столбце выписаны: часть искомой кучи есть , удвоенное это число: и учетверенное: . Сумма этих трех чисел, равная числу , есть произведение первоначального предположения 7 на .

Итак, куча равна .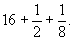

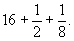
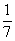
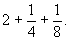
В последнем столбце Ахмес делает проверку, складывая полученное значение для кучи и его части . В сумме получается 19, и решение заканчивается обычным для автора заключением: “Будет хорошо”.

Способ решения, примененный Ахмесом, называется методом одного ложного положения. При помощи этого метода решаются уравнения вида ах == b. Его применяли как египтяне, так и вавилоняне.

У разных народов применялся метод двух ложных положений. Арабами этот метод был механизирован и получил ту форму, в которой он перешел в учебники европейских народов, в том числе в “Арифметику” Магницкого. Магницкий называет способ решения “фальшивым правилом” и пишет о части своей книги, излагающей этот метод:

Зело бо хитра есть сия часть,

Яко можеши ею все класть (вычислить. — И . Д.)

Не токмо что есть во гражданстве,

Но и высших наук в пространстве,

Яже числятся в сфере неба,

Якоже мудрым есть потреба.

Содержание стихов Магницкого можно вкратце передать так: эта часть арифметики весьма хитрая. При помощи ее можно вычислить не только то, что понадобится в житейской практике, но она решает и вопросы “высшие”, которые встают перед “мудрыми”.

Магницкий пользуется “фальшивым правилом” в форме, какую ему придали арабы, называя его “арифметикой двух ошибок” или “методой весов”.

Квадратные уравнения в Древнем Вавилоне

Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:

Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.

Несмотря на высокий уровень развития алгебры в Вавилоне, • в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.

. Как составлял и решал Диофант квадратные уравнения ,

В “Арифметике” Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.

При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.

Вот, к примеру, одна из его задач.

“Найти два числа, зная, что их сумма равна 20, а произведение — 96”.

Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т. е. 10 + х, другое же меньше, т. е. 10 — х. Разность между ними 2х. Отсюда уравнение

Отсюда х = 2. Одно из искомых чисел равно 12, другое 8. Решение х = —2 для Диофанта не существует, так как греческая математика знала только положительные числа.

Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения

Ясно, что, выбирая в качестве неизвестного полу разность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).

Квадратные уравнения в Индии.

Задачи на уравнения встречаются уже в астрономическом трактате “Ариабхаттаим”, составленном в 449 г. индийским математиком и астрономом Арибхаттой. Но это уже раннее средневековье.

В Алгебраическом трактате ал-Хорезми даётся классификация линейных и квадратных уравнений.

Индий учёные знали решения неопределённых уравнений в целых числах (в том числе и в отрицательных, чего сам Диофант избегал).

Формула решений квадратного уравнения.

Греческий математик Герон (I или II век нашего летоисчисления) вывел формулу для решения квадратного равнения ax 2 + bx = c умножением всех членов на а и

прибавлением к обеим половинам уравнения :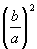

В индии пришли к более простому способу вывода, который встречается в школьных учебниках: они умножали на 4a и к обеим половинам по b 2 . Это даёт:

Индийские математики часто давали задачи в стихах.

Задача о лотосе.

Над озером тихим, с полмеры над водой,

Был виден лотоса цвет.

Он рос одиноко, и ветер волной

Нагнул его в сторону – и уж нет

Цветка над водой.

Нашёл его глаз рыбака

В двух мерах от места, где рос.

Сколько озера здесь вода глубока?

Тебе предложу я вопрос.

Ответ:

Из истории решения системы уравнений, содержащей одно уравнение второй степени и одно линейное

В древневавилонских текстах, написанных в III—II тысячелетиях до н. э., содержится немало задач, решаемых с помощью составления систем уравнений, в которые входят и уравнения второй степени. Вот одна из них.

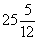
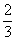
. “Площади двух своих квадратов я сложил: .Сторона второго квадрата равна стороны первого и еще 5”.

Соответствующая система уравнений в современной записи имеет вид:

Для решения системы (1) вавилонский автор возводит во втором уравнении у в квадрат и согласно формуле квадрата суммы, которая ему, видимо, была известна, получает:

Подставляя это значение у в первое из системы уравнений (1), автор приходит к квадратному уравнению:

Решая это уравнение по правилу, применяемому нами в настоящее время, автор находит х, после чего определяет у. Итак, хотя вавилоняне и не имели алгебраической символики, они решали задачи алгебраическим методом.

Диофант, который не имел обозначений для многих неизвестных, прилагал немало усилий для выбора неизвестного таким образом, чтобы свести решение системы к решению одного уравнения. Вот один пример из его “Арифметики”.

Задача 21. “Найти два числа, зная, что их сумма равна 20, а сумма их квадратов — 208”.

Эту задачу мы решили бы путем составления системы уравнений:

Диофант же, выбирая в качестве неизвестного половину разности искомых чисел, получает (в современных обозначениях):

Складывая эти уравнения, а затем вычитая одно из другого (все это Диофант производит устно), получаем

x = 2 + 10; у = 10 —2.

х 2 + у 2 = (г + lO) 2 + (10 — г) 2 == 2z 2 + 200.

z = 2; х = 2 + 10 = 12; у = 10 — 2 = 8.

Задача Диофанта №80 (Из II книги его “Арифметики”)

Найти 2 таких числа, чтобы сумма квадрата каждого из них с другим искомым числом дала полный квадрат,

Пусть первое число (I) будет s. Чтобы квадрат его •при прибавлении второго числа дал квадрат, второе число должно быть 2s + 1, так как в таком случае выполняется требование задачи: квадрат первого числа. сложенный со вторым, дает

s 2 + 2s + 1, то есть полный квадрат (s + 1) 2 .

Квадрат второго числа, сложенный с первым, должен также дать квадрат, то есть число (2s + I) 2 + s, равное

4s 2 + 5s + 1 == t 2

Положим, что t = 2s — 2; тогда t 2 = 4s 2 — 8s + 4. Это выражение должно равняться 4s 2 + 5s + 1. Итак, должно быть:

4s 2 — 8s + 4 == 4s 2 + 5s + l откуда s=

Значит, задаче удовлетворяют числа:

.

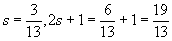
Почему Диофант делает предположение, что t==2s—2, он не объясняет. Во всех своих задачах (в дошедших до нас шести книгах его их 189) он делает то или другое предположение, не давая никакого обоснования.

Вообще содержание 6 книг таково:

В “Арифметике” 189 задач, каждая снабжена одним или несколькими решениями. Задачи ставятся в общем виде, затем берутся конкретные значения входящих в нее величин и даются решения.

Задачи книги I в большинстве определенные. В ней имеются и такие, которые решаются с помощью систем двух уравнений с двумя неизвестными, эквивалентных квадратному уравнению. Для его разрешимости Диофант выдвигает условие, чтобы дискриминант был полным квадратом. Так, задача 30— найти таких два числа, чтобы их разность и произведение были заданными числами,— приводится к системе

Диофант выдвигает “условие формирования”: требуется, чтобы учетверенное произведение чисел, сложенное с квадратом разности их, было квадратом, т. е. 4b + а 2 = с 2 .

В книге II решаются задачи, связанные с неопределенными уравнениями и системами таких уравнений с 2, 3, 4, 5, 6 неизвестными степени не выше второй.

Диофант применяет различные приемы. Пусть необходимо решить неопределенное уравнение второй степени с двумя неизвестными f 2 (х, у) ==0. Если у него есть рациональное решение (x 0 , y 0 ), то Диофант вводит подстановку

в которой k рационально. После этого основное уравнение преобразуется в квадратное относительно t, у которого свободный член f 2 ( x 0 , у 0 ) = 0. Из уравнения получается t 1 == 0 (это значение Диофант отбрасывает), t 2 — рациональное число. Тогда подстановка дает рациональные х и у.

В случае, когда задача приводилась к уравнению у 2 = ax 2 + bx + с, очевидно рациональное решение x 0 = О, y 0 =±C . Подстановка Диофанта выглядит так:

Другим методом при решении задач книги II Диофант пользовался, когда они приводили к уравнению у 2 == = a 2 x 2 + bx + с. Он делал подстановку

после чего х и у выражались рационально через параметр k:

Диофант, по существу, применял теорему, состоящую в том,; что если неопределенное уравнение имеет хотя бы одно рациональное решение, то таких решений будет бесчисленное множество, причем значения х и у могут быть представлены в виде рациональных функций некоторого параметра”

В книге II есть задачи, решаемые с помощью “двойного неравенства”, т. е. системы

Диофант рассматривает случай а = с, но впоследствии пишет, что метод можно применить и при а : с = т 2 , Когда а == с, Диофант почленным вычитанием одного равенства из другого получает и 2 — и 2 = b — d. Затем разность b — d раскладывается на множители b — d = п1 и приравнивает и + v = I, и — v = п, после чего находит

и = (I + п)/2, v = (I — n)/2, х — ( l 2 + п 2 >/4a —

Если задача сводится к системе из двух или трех уравнений второй степени, то Диофант находит такие рациональные выражения неизвестных через одно неизвестное и параметры, при которых все уравнения, кроме одного, обращаются в тождества. Из оставшегося уравнения он выражает основное неизвестное через параметры, а затем находит и другие неизвестные.

Методы, разработанные в книге II, Диофант применяет к более трудным задачам книги III, связанным с системами трех, четырех и большего числа уравнений степени не выше второй. Он, кроме того, до формального решения задач проводит исследования и находит условия, которым должны удовлетворять параметры, чтобы решения существовали.

В книге IV встречаются определенные и неопределенные уравнения третьей и более высоких степеней. Здесь дело обстоит значительно сложнее, потому что, вообще говоря, неизвестные невозможно выразить как рациональные функции одного параметра. Но, как и раньше, если известны одна или две рациональные точки кубической кривой fз (х, у) == 0, то можно найти и другие точки. Диофант при решении задач книги IV применяет новые методы”

Книга V содержит наиболее сложные задачи; некоторые из них решаются с помощью уравнений третьей и четвертой степеней от трех и более неизвестных. Есть и такие, в которых требуется разложить данное целое число на сумму двух, трех или четырех квадратов, причем эти квадраты должны удовлетворить определенным неравенствам.,

При решении задач Диофант дважды рассматривает уравнение Пелля ax 2 + 1 = у 2 .

Задачи книги VI касаются прямоугольных треугольников с рациональными сторонами. К условию х 2 + у 2 == z 2 в них добавляются еще условия относительно площадей, периметров, сторон треугольников.

В книге VI доказывается, что если уравнение ax 2 + b == у 2 имеет хотя бы одно рациональное решение, то их будет бесчисленное множество. Для решения задач книги VI Диофант применяет все употребляемые им способы.

Кстати, в одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраиче-юй загадки, представляющей надгробную надпись на его могиле

Прах Диофанта гробница покоит; дивись ей—и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругою он обручился.

С нею пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей.

Задача-загадка сводится к составлению и решению уравнения:

откуда х = 84 = вот сколько лет жил Диофант.

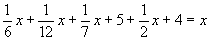
Неопределённое уравнение x 2 + y 2 = z 2

Такое неопределённое уравнение исследовали пиффагорийцы, целые решения которого поэтому называют “пифагоровыми тройками”, они нашли бесконечно много таких троек, имеющих вид:

Более систематическое исследование задач, эквивалентных кубическим уравнениям, относится только к эпохе эллинизма. Архимед в сочинении “О шаре и цилиндре” (книга II, предложение 4) свел задачу о рассечении шара плоскостью на два сегмента, объемы которых имели бы заданное отношение т : п (т > п), к нахождению высоты х большего сегмента из пропорции

(1)

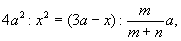
где а — радиус шара.

Архимед обобщает задачу: рассечь заданный отрезок а на две части х и а — х так, чтобы

(а — х) : с = S : х 2 , (2)

где с и S — заданные отрезок и площадь.

Заметив, что при такой общей постановке задача не всегда разрешима (имеются в виду только положительные действительные решения), Архимед приступает к ее исследованию с тем, чтобы наложить ограничения на с и S. Он говорит, что изложит полное решение задачи “в конце”, однако соответствующее место не сохранилось. Жившие на столетие позже Архимеда греческие геометры Диокл и Дионисодор уже не знали его. Они предложили собственные, гораздо более сложные решения, но никто из них не сумел провести анализ общего случая.

Только в VI в. н. э. комментатор Архимеда Евтокий нашел утраченное место. Архимед решает задачу с помощью двух конических сечений:

(3)

(4)

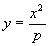
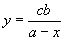
(здесь положено S = pb ). Оба уравнения легко получить из пропорции (2). Для выяснения необходимых условий Архимед переходит от пропорции (2) к кубическому уравнению

которое он выражает словесно как соотношение между объемами. Ясно, что уравнение (5) может иметь положительные корни, если

Итак, проблема сводится к нахождению экстремума х 2 (а — х).

Оставим пока в стороне вопрос о методе экстремумов Архимеда, мы вернемся к этому, когда будем говорить об инфинитезимальных методах древних. Скажем только, что Архимед полностью исследовал условия существования положительных вещественных корней уравнения (5), а именно:

1) если Sc 3 /27, то на участке (0, а) имеются два таких корня;

2) если Sc = 4a з /27, то имеется один корень (как сказали бы мы,— двукратный);

3) если Sc > 4a з /27, то корня нет.

Здесь 4а 3 /27 есть максимум х 2 (а — х) , достигаемый при х = 2а/3 . В конце письма, предпосланного книге “О коноидах и сфероидах” (греки называли сфероидами эллипсоиды вращения, прямоугольными коноидами — параболоиды вращения, а тупоугольными коноидами — полости двуполостных гиперболоидов вращения), Архимед пишет, что с помощью доказанных в книге теорем можно решить ряд задач, как, например: от данного сфероида или коноида отсечь сегмент плоскостью, проведенной параллельно заданной, так, чтобы отсеченный сегмент был равен данному конусу, цилиндру или шару. Перечисленные задачи, так же как и задачи о делении шара, сводятся к кубическим уравнениям, причем в случае тупоугольного коноида уравнение будет иметь вид

Из текста Архимеда можно заключить, что он проанализировал и решил это уравнение. Таким образом, Архимед рассмотрел кубические уравнения вида х 3 + ax + b = 0 при различных значениях a и b и дал метод их решения. Однако исследование кубических уравнений оставалось для греков трудной задачей, с которой, в ее общем виде никто, кроме Архимеда, не мог справиться. Решение отдельных задач, эквивалентных кубическим уравнениям, греческие математики получали с помощью нового геометрического аппарата конических сечений. Этот метод впоследствии восприняли математики стран ислама, которые сделали попытку провести полный анализ всех уравнений третьей степени.

Но еще до этого, и притом греческими математиками, был сделан новый решительный шаг в развитии алгебры: геометрическая оболочка была сброшена, и началось построение буквенной алгебры на основе арифметики. Это произошло в первые века нашей эры.

“История математики в древности” Э. Кольман.

“Решение уравнений в целых числах” Гельфонд.

“В мире уравнений” В.А.Никифоровский.

“История математики в школе” Г.И.Глейзер.

“Рассказы о старой и новой алгебре” И.Депман.

“Пифагор: рассказы о математике” Чистаков.

“Краткий очерк истории математики” Стройк Д.Я.

“Очерки по истории математики” Болгарский Б.В.

“История математики” (энциклопедия) под редакцией Юшкевича.

“Энциклопедический словарь юного математика” под редакцией Гнеденко.