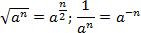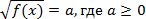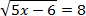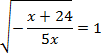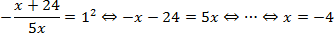Как решаются показательные логарифмические уравнения

Решение показательных уравнений методом логарифмирования

Знакомство с логарифмом числа открывает возможность использования метода логарифмирования для решения уравнений. Преимущественно методом логарифмирования решаются показательные уравнения. В этой статье мы подробно разберем, как проводится решение показательных уравнений методом логарифмирования. Здесь мы дадим необходимую теорию и, конечно же, рассмотрим характерный пример решения показательного уравнения методом логарифмирования.

Теория

Решение каких показательных уравнений проводится методом логарифмирования

В основном, методом логарифмирования решаются показательные уравнения в двух следующих случаях:

• В одной части уравнения находится степень, произведение или частное степеней, а в другой – положительное число. Например, 2 x−1 =10 , и др.
• И в одной, и в другой части уравнения находится степень, произведение или частное степеней, возможно с положительным числовым коэффициентом. Например, 3 x 2 −1 =5·2 x+1 и др.

Как проводится решение

Во-первых, нужно убедиться, что обе части показательного уравнения принимают только положительные значения на ОДЗ для исходного уравнения. Во-вторых, проводится логарифмирование обеих частей уравнения по одному и тому же положительному и отличному от единицы основанию. В-третьих, решается уравнение, полученное в результате логарифмирования. Это дает решение исходного уравнения.

По какому основанию логарифмировать

В принципе, в качестве основания логарифма можно брать любое положительное и отличное от единицы число. Обычно логарифмирование проводят по основанию, равному основанию одной из степеней, фигурирующих в исходном уравнении. Также в ходу основание 10 . Это удобно тем, что дает возможность проводить некоторые попутные вычисления при помощи таблицы десятичных логарифмов.

Пример решения показательного уравнения

Рассмотрим характерный пример решения показательного уравнения методом логарифмирования.

Решите показательное уравнение .

Алгебра

План урока:

Задание. Укажите корень логарифмического уравнения

Задание. Решите урав-ние

В чуть более сложных случаях под знаком логарифма может стоять не сама переменная х, а выражение с переменной. То есть урав-ние имеет вид

Задание. Найдите решение логарифмического уравнения

Задание. Решите урав-ние

Задание. Решите урав-ние

Получили показательное уравнение. Показатели степеней можно приравнять, если равны их основания:

Уравнения вида log_af(x) = log_ag(x)

Порою логарифм стоит в обеих частях равенства, то есть и слева, и справа от знака «равно». Если основания логарифмов совпадают, то должны совпадать и аргументы логарифмов.

Задание. Решите урав-ние

Задание. Найдите корень урав-ния

Ситуация несколько усложняется в том случае, когда, под знаком логарифма в обоих частях равенства стоят выражения с переменными, то есть оно имеет вид

С одной стороны, очевидно, что должно выполняться равенство f(x) = g(x). Но этого мало, ведь под знаком логарифма не должно стоять отрицательное число. Поэтому после получения корней следует подставить их в урав-ние и убедиться, что они не являются посторонними корнями.

Задание. Решите урав-ние

Получили квадратное уравнение, которое решаем с помощью дискриминанта:

Получили два корня, (– 3) и 4. Однако теперь подставим их в исходное урав-ние и посмотрим, что у нас получится. При х = – 3 имеем:

Это верное равенство, поэтому х = – 3 действительно является корнем урав-ния. Теперь проверяем х = 4:

Хотя выражения и справа, и слева одинаковы, равенство верным считать нельзя, ведь выражение log₃ (– 1) не имеет смысла! Действительно, нельзя вычислять логарифм от отрицательного числа. Поэтому корень х = 4 оказывается посторонним, и у нас остается только один настоящий корень – число (– 3).

Уравнения, требующие предварительных преобразований

Естественно, не всегда в обоих частях логарифмических уравнений и неравенств стоят только логарифмы с совпадающими основаниями. Часто требуется выполнить некоторые предварительные преобразования, чтобы привести урав-ние к виду log_af(x) = log_ag(x).

Задание. Решите урав-ние

с помощью которой любой множитель можно внести под знак логарифма. Сделаем это и в нашем случае:

Теперь в обеих частях равенства не стоит ничего, кроме логарифмов с одинаковыми основаниями. Поэтому мы можем приравнять их аргументы:

Задание. Решите урав-ние

Снова проверяем каждый из корней, подставляя его в исходное ур-ние. Прих = –1 получаем

Задание. Решите урав-ние

Решение. В правой части снова стоит сумма, но на этот раз не логарифмов. Однако число 1 можно представить как log₅ 5. Тогда урав-ние можно преобразовать:

Задание. Решите урав-ние

Решение. Данный пример похож на простейшее логарифмическое уравнение, однако переменная находится в основании логарифма, а не в аргументе. По определению логарифма мы можем записать, что

Первый вариант придется отбросить, так как основание логарифма, (а в данном случае это выражение х – 5) не может быть отрицательным числом. Получается, что

Задание. Решите урав-ние

Решение. Здесь ситуация осложняется тем, что основания логарифмов разные. Поэтому один из них необходимо привести к новому основанию. Попробуем привести log₂₅x 4 к основанию 5, используя известную нам формулу

Мы добились того, что у логарифмов одинаковые основания, а потому мы можем приравнять их аргументы:

Логарифмические уравнения с заменой переменных

Иногда приходится делать некоторые замены, чтобы уравнение приняло более привычный вид.

Задание. Решите уравнение методом замены переменной

Задание. Найдите решение уравнения методом замены переменной

Решение. Для начала напомним, что символ lg означает десятичный логарифм. Отдельно знаменатель дроби в правой части:

Логарифмирование уравнений

Ясно, что если от равных величин взять логарифмы по одному и тому же основанию, то тогда эти логарифмы окажутся также равными. Если подобный прием применяют при решении урав-ния, то, говорят, что производится логарифмирование уравнения. Иногда оно позволяет решить некоторые особо сложные примеры.

Задание. Укажите корни урав-ния

Здесь переменная величина находится одновременно и в основании степени, и в ее показателе. Возьмем от правой и левой части урав-ния логарифм по основанию 5:

Возвращаемся от переменной t к переменной х:

Переход от логарифмических неравенств к нелогарифмическим

Рассмотрим график логарифмической функции у = log_ax при условии а > 1. Она является возрастающей функцией. Если на оси Ох отложить два числа tи s так, чтобы t располагалось левее s (то есть t 1). Но это не совсем так. Дело в том, что надо учесть ещё и тот факт, что под знаком логарифма может стоять исключительно положительное число. Получается, что от простейшего логарифмического неравенства

Естественно, вместо величин t и s могут стоять как числа, так и выражения с переменными.

Задание. Найдите решение логарифмического неравенства

Ответ можно оставить и в такой форме, однако всё же принято записывать его в виде промежутка. Очевидно, что нерав-во 0 log_as:

Но, снова-таки, мы должны учесть, числа t может быть лишь положительным (тогда s, которое больше t, автоматически также окажется положительным). Получается, что при 0 log_a s можно перейти к двойному нерав-ву 0 2 – 45х + 200 имеет решение

Однако в системе (5) есть ещё два неравенства, х > 0 и 45 >x. Их решениями являются промежутки (0; + ∞) и (– ∞; 45). Чтобы определить решение всей системы, отметим на одной прямой решения каждого отдельного нерав-ва и найдем область их пересечения:

Видно, что решениями нерав-ва будут являться промежутки (0; 5) и (40; 45), на которых справедливы все три нерав-ва, входящих в систему (5).

Задача B7 — логарифмические, показательные и иррациональные уравнения

Все задачи B7, которые мне доводилось видеть, были сформулированы примерно одинаково: решить уравнение. При этом сами уравнения относятся к одному из трех видов:

1. Логарифмические;
2. Показательные;
3. Иррациональные.

Вообще говоря, полноценное руководство по каждому типу уравнений займет не один десяток страниц, выходя далеко за рамки ЕГЭ. Поэтому мы рассмотрим лишь самые простые случаи, требующие незатейливых рассуждений и выкладок. Этих знаний будет вполне достаточно, чтобы решить любую задачу B7.

В математике термин «решить уравнение» означает найти множество всех корней данного уравнения, либо доказать, что это множество пусто. Но в бланк ЕГЭ можно вписывать только числа — никаких множеств. Поэтому, если в задании B7 оказалось больше одного корня (или, наоборот, ни одного) — в решении была допущена ошибка.

Логарифмические уравнения

— это любое уравнение, которое сводится к виду log _a f ( x ) = k , где a > 0, a ≠ 1 — основание логарифма, f ( x ) — произвольная функция, k — некоторая постоянная.

Такое уравнение решается внесением постоянной k под знак логарифма: k = log _a a k . Основание нового логарифма равно основанию исходного. Получим уравнение log _a f ( x ) = log _a a k , которое решается отбрасыванием логарифма.

Заметим, что по условию a > 0, поэтому f ( x ) = a k > 0, т.е. исходный логарифм существует.

Решение. log₇ (8 − x ) = 2 ⇔ log₇ (8 − x ) = log₇ 7 2 ⇔ 8 − x = 49 ⇔ x = −41.

Решение. log_0,5 (6 − x ) = −2 ⇔ log_0,5 (6 − x ) = log_0,5 0,5 −2 ⇔ 6 − x = 4 ⇔ x = 2.

Но что делать, если исходное уравнение окажется сложнее, чем стандартное log _a f ( x ) = k ? Тогда сводим его к стандартному, собирая все логарифмы в одной стороне, а числа — в другой.

Если в исходном уравнении присутствует более одного логарифма, придется искать область допустимых значений (ОДЗ) каждой функции, стоящей под логарифмом. Иначе могут появиться лишние корни.

Поскольку в уравнении присутствуют два логарифма, найдем ОДЗ:

1. x + 1 > 0 ⇔ x > −1
2. x + 5 > 0 ⇔ x > −5

Получаем, что ОДЗ — это интервал (−1, +∞). Теперь решаем уравнение:

log₅ ( x + 1) + log₅ ( x + 5) = 1 ⇒ log₅ ( x + 1)( x + 5) = 1 ⇔ log₅ ( x + 1)( x + 5) = log₅ 5 1 ⇔ ( x + 1)( x + 5) = 5 ⇔ x 2 + 6 x + 5 = 5 ⇔ x ( x + 6) = 0 ⇔ x ₁ = 0, x ₂ = −6.

Но x ₂ = −6 не подходит по ОДЗ. Остается корень x ₁ = 0.

Показательные уравнения

— это любое уравнение, которое сводится к виду a f ( x ) = k , где a > 0, a ≠ 1 — основание степени, f ( x ) — произвольная функция, k — некоторая постоянная.

Это определение почти дословно повторяет определение логарифмического уравнения. Решаются показательные уравнения даже проще, чем логарифмические, ведь здесь не требуется, чтобы функция f ( x ) была положительна.

Для решения сделаем замену k = a t , где t — вообще говоря, логарифм ( t = log _a k ), но в ЕГЭ числа a и k будут подобраны так, что найти t будет легко. В полученном уравнении a f ( x ) = a t основания равны, а значит, равны и показатели, т.е. f ( x ) = t . Решение последнего уравнения, как правило, не вызывает проблем.

Задача. Решить уравнение: 7 x − 2 = 49.

Решение. 7 x − 2 = 49 ⇔ 7 x − 2 = 7 2 ⇔ x − 2 = 2 ⇔ x = 4.

Задача. Решить уравнение: 6 16 − x = 1/36.

Решение. 6 16 − x = 1/36 ⇔ 6 16 − x = 6 −2 ⇔ 16 − x = −2 ⇔ x = 18.

Немного о преобразовании показательных уравнений. Если исходное уравнение отличается от a f ( x ) = k , применяем правила работы со степенями:

1. a n · a m = a n + m ,
2. a n / a m = a n − m ,
3. ( a n ) m = a n · m .

Кроме того, надо знать правила замены корней и дробей на степени с рациональным показателем:

Такие уравнения встречаются в ЕГЭ крайне редко, но без них разбор задачи B7 был бы неполным.

Задача. Решить уравнение: (5/7) x − 2 · (7/5) 2 x − 1 = 125/343

1. (7/5) 2 x − 1 = ((5/7) −1 ) 2 x − 1 = (5/7) 1 − 2 x ,
2. 125/343 = (5 3) /(7 3 ) = (5/7) 3 .

Имеем: (5/7) x − 2 · (7/5) 2 x − 1 = 125/343 ⇔ (5/7) x − 2 · (5/7) 1 − 2 x = (5/7) 3 ⇔ (5/7) x − 2 + 1 − 2 x = (5/7) 3 ⇔ (5/7) − x − 1 = (5/7) 3 ⇔ − x − 1 = 3 ⇔ x = −4.

Иррациональные уравнения

Под иррациональным понимается любое уравнение, содержащее знак корня. Из всего многообразия иррациональных уравнений мы рассмотрим лишь простейший случай, когда уравнение имеет вид:

Чтобы решить такое уравнение, возведем обе стороны в квадрат. Получим уравнение f ( x ) = a 2 . При этом автоматически выполняется требование ОДЗ: f ( x ) ≥ 0, т.к. a 2 ≥ 0. Остается решить несложное уравнение f ( x ) = a 2 .

Возводим обе стороны в квадрат и получим: 5 x − 6 = 8 2 ⇔ 5 x − 6 = 64 ⇔ 5 x = 70 ⇔ x = 14.

Сначала, как и в прошлый раз, возводим обе стороны в квадрат. А затем внесем знак «минус» в числитель. Имеем:

Заметим, что при x = −4 под корнем будет положительное число, т.е. требование ОДЗ выполнено.