Как решить дифференциальное уравнение первого порядка

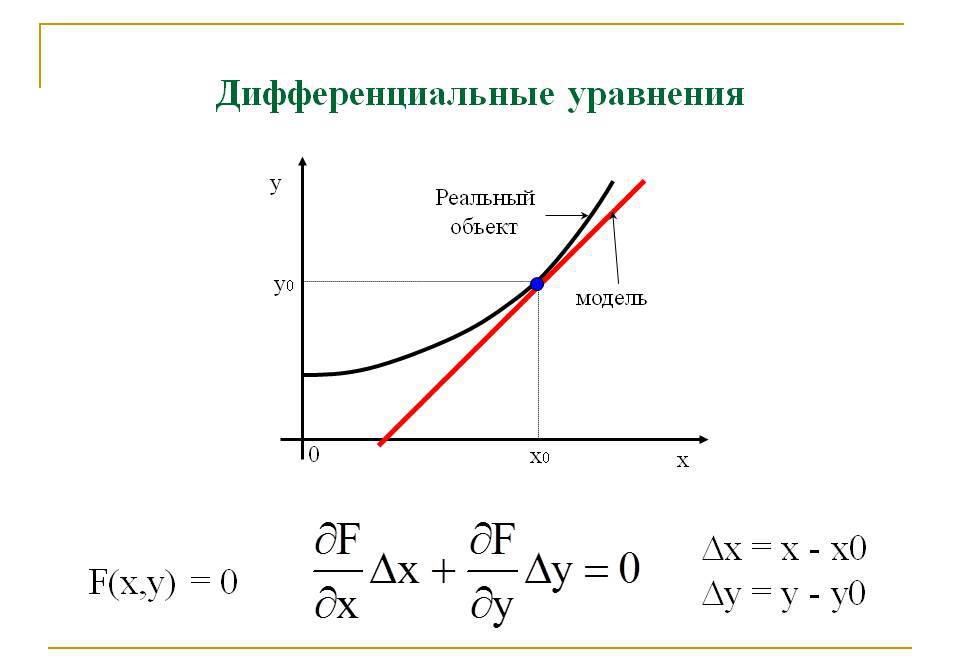
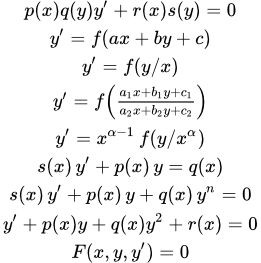Дифференциальные уравнения первого порядка

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Как решать дифференциальные уравнения первого порядка

Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .

Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.

Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.

Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.

Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.

Уравнения с разделяющимися переменными

Уравнения, приводящиеся к уравнениям с разделяющимися переменными

Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>

Однородные уравнения

Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>

Уравнения, приводящиеся к однородным

Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>

Обобщенные однородные уравнения

Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>

Линейные дифференциальные уравнения

Есть три метода решения линейных уравнений.

1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>

2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>

3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:

Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>

Уравнения Бернулли

Подстановкой уравнение Бернулли приводится к линейному уравнению.

Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .

Уравнения Риккати

Оно не решается в общем виде. Подстановкой

уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:

оно приводится к виду:
,
где .

Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>

Уравнения Якоби

Уравнения в полных дифференциалах

При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.

Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция , при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>

Уравнения, не решенные относительно производной y’

Уравнения, допускающие решение относительно производной y’

Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, допускающие разложение на множители

Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;

;
Подробнее >>>

Уравнения, не содержащие x и y

Уравнения, не содержащие x или y

или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .

Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>

Уравнения, разрешенные относительно y

Уравнения Клеро

Такое уравнение имеет общее решение

Подробнее >>>

Уравнения Лагранжа

Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>

Уравнения, приводящиеся к уравнению Бернулли

Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 20-05-2016

Дифференциальные уравнения первого порядка — особенности решения и примеры

Одной из самых сложных и непонятных тем вузовской математики становятся интегрирование и дифференциальное исчисление. Необходимо знать и разбираться в этих понятиях, а также уметь их применять. Многие вузовские технические дисциплины завязаны на дифференциалах и интегралах.

Краткая информация про уравнения

Данные уравнения являются одним из важнейших математических понятий в образовательной системе. Дифференциальное уравнение — это уравнение, которое связывает независимые переменные, функцию, которую необходимо отыскать и производные этой функции переменным, которые считаются независимыми. Дифференциальное исчисление для отыскания функции одной переменной называется обыкновенным. Если искомая функция зависит от нескольких переменных, то говорят об уравнении в частных производных.

По сути, нахождение некого ответа уравнения сводится к интегрированию, а метод решения определяется видом уравнения.

Уравнения 1-го порядка

Дифференциальное уравнение первого порядка — такое уравнение, которое способно описать переменную, нужную функцию и ее первую производную. Такие уравнения могут быть заданы в трех видах: явная, неявная, дифференциальная.

Понятия, необходимые для решения

Начальное условие — задание значения искомой функции при заданном значении переменной, которая является независимой.

Решение дифференциального уравнения — любая дифференцируемая функция, точно подставленная в исходное уравнение, обращает его в тождественно равное. Решение полученное, не являющееся явным, есть интеграл уравнения.

Общее решение дифференциальных уравнений — это функция y = y(x;C), которая может удовлетворять следующим суждениям:

1. Функция может иметь только одну произвольную постоянную С.
2. Полученная функция должна быть решением уравнения при любых произвольных значениях произвольной постоянной.
3. При заданном начальном условии произвольную постоянную можно определить единственным образом так, что полученное частное решение будет согласовываться с заданным раннее начальным условием.

На практике часто используется задача Коши — отыскание такого решения, которое является частным и может сравниться с условием, поставленным в начале.

Теорема Коши — теорема, которая подчеркивает существование и единственность частного решения в дифференциальных исчислениях.

• Общее решение y = y(x;C) уравнения есть общее количество интегральных кривых.
• Дифференциальное исчисление позволяет связать координаты точки плоскости XOY и касательную, которая проведена к интегральной кривой.
• Задание исходного условия означает задание точки на плоскости.
• Решить задачу Коши означает, что из всего множества интегральных кривых, представляющих одинаковое решение уравнения, необходимо отобрать ту единственную, проходящую через единственную возможную точку.
• Выполнение условий теоремы Коши в точке означает, что через выбранную точку в плоскости обязательно проходит (притом, только одна) интегральная кривая.

Уравнение с разделяющимися переменными

По определению, дифференциальное уравнение — это такое уравнение, где его правая часть описывает собой или отражена в виде произведения (иногда отношения) двух функций, одна, зависящая только от «х», а другая — только от «y». Ясный пример для такого вида: y’ = f1(x)*f2(y).

Чтобы решить уравнения конкретной формы, требуется сначала преобразовать производную y’ = dy/dx. Затем нужно с помощью манипуляций с уравнением привести его к такому виду, когда можно интегрировать две части уравнения. После необходимых преобразований интегрируем обе части и упрощаем полученный результат.

Однородные уравнения

По определению, дифференциальное уравнение можно именовать однородным, если оно имеет следующую форму: y’ = g(y/x).

При этом чаще всего используется замена y/x = t(x).

Для решения подобных уравнений необходимо свести однородное уравнение к виду с разделяющимися переменными. Для этого необходимо произвести следующие операции:

1. Отобразить, выражая производную изначальной функции, из любой исходной в виде нового уравнения.
2. Следующим шагом необходимо преобразовать полученную функцию в вид f(x;y) = g(y/x). Более простыми словами — сделать так, чтобы уравнение содержало только отношение y/x и константы.
3. Произвести следующую замену: y/x = t(x); y = t(x)*x; y’ = t’*x + t. Произведенное замещение поможет поделить в уравнении переменные, постепенно приводя его к более простой форме.

Линейные уравнения

Определение таких уравнений выглядит следующим образом: линейное дифференциальное уравнение — это такое уравнение, где его правая часть выражается как линейное выражение относительно изначальной функции. Искомая функция в этом случае: y’ = a(x)*y + b(x).

Перефразируем определение следующим образом: любое уравнение 1-го порядка станет линейным по своему виду, если изначальная функция и ее производная от нее включены в уравнение первых степенях и не умножаются на друг друга. «Классический вид» линейного диф-уравнения имеет следующую структуру: y’ + P(x)y = Q(x).

Прежде чем решать такое уравнение, следует преобразовать его к «классической форме». Следующим этапом станет выбор способа решений: способ Бернулли или методика Лагранжа.

Решение уравнения с помощью метода, который ввел Бернулли, подразумевает собой подстановку и сведение линейного дифференциального уравнения к двум уравнениям с раздельными переменными сравнительно функций U(x), а также V(x), которые были даны в первоначальном виде.

Метод Лагранжа заключается в поиске общего решения исходного уравнения.

1. Следует отыскать одинаковое решение однородного уравнения. После поиска имеем функцию y = y(x,C), где C — произвольная постоянная.
2. Ведем поиск решения изначального уравнения в той же форме, но считаем C = C(x). Подставляем функцию y = y(x,C(x)) в изначальное уравнение, отыскиваем функцию C(x) и записываем решение общего исходного уравнения.

Уравнение Бернулли

Уравнение Бернулли — если правая часть исчисления принимает вид f(x;y) = a(x)y + b(x)yk, где k — любое возможное рациональное числовое значение, не беря в пример случаи, когда k = 0 и k = 1.

Если k = 1, то исчисление принимает вид с разделяющимися переменными, а при k = 0 уравнение остается линейным.

Рассмотрим общий случай решения данного типа уравнения. Имеем стандартное уравнение Бернулли. Его необходимо свести к линейному, для этого нужно поделить уравнение на yk. После этой операции произвести замену z(x) = y1-k. После ряда преобразований уравнение будет сводиться к линейному, чаще всего методом подстановки z = U*V.

Уравнения в полных дифференциалах

Определение. Уравнение, имеющее структуру P(x;y)dx + Q(x;y)dy = 0 именуется уравнением в полных дифференциалах, в том случае, если соблюдается следующее условие (в этом условии «d» — частный дифференциал): dP(x;y)/dy = dQ(x;y)/dx.

Все раннее рассмотренные первого порядка дифференциальные уравнения можно отобразить в виде дифференциалов.

Такие исчисления решаются несколькими способами. Но, однако, все они начинаются с проверки выполнения условия. Если условие выполнено, то крайняя левая область уравнения есть полный дифференциал, пока неизвестной функции U(x;y). Тогда, в соответствии с уравнением, dU(x;y) будет равно нулю, и поэтому одинаковый интеграл уравнения в полных дифференциалах будет отображаться в виде U(x;y) = С. Поэтому решение уравнения приводится к отысканию функции U(x;y).

Интегрирующий множитель

Если в уравнении условие dP(x;y)/dy = dQ(x;y)/dx не выполняется, то уравнение не имеет вид, который мы рассмотрели пунктом выше. Но иногда можно подобрать некоторую функцию M(x;y), при умножении на которую уравнение принимает вид уравнения в полных «диффурах». Функция M (x;y) именуется как интегрирующий множитель.

Интегрирующий можно найти только в тех случаях, когда он становится функцией исключительно для одной переменной.

Примеры решения дифференциальных уравнений с ответами

Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения дифференциальных уравнений

Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.

Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.

Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.

Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).

Примеры решения дифференциальных уравнений

Задание

Решить дифференциальное уравнение xy’=y.

Решение

В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь

переписываем дифференциальное уравнение, получаем

Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем

Далее интегрируем полученное уравнение:

В данном случае интегралы берём из таблицы:

После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.

– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const

Ответ

Задание

Найти частное решение дифференциального уравнения

Решение

Действуем по тому же алгоритму, что и в предыдущем решении.

Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:

Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:

Если – это константа, то

0\]» title=»Rendered by QuickLaTeX.com» />

– тоже некоторая константа, заменим её буквой С:

– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.

Получаем общее решение:

Ответ

Задание

Решить дифференциальное уравнение

Решение

В первую очередь необходимо переписать производную в необходимом виде:

Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:

После разделения переменных, интегрируем уравнение, как в примерах выше.

Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:

В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.

Далее упрощаем общий интеграл:

Приводим полученный общий интеграл к виду: F(x,y)=C:

Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(0)=ln2.

Решение

Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.

Начинаем разделять переменные и интегрировать уравнение:

Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.

Получаем общее решение:

Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.

В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Задание

Решить дифференциальное уравнение

Решение

При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:

В данном случае константу C считается не обязательным определять под логарифм.

Ответ

Задание

Найти частное решение дифференциального уравнения

удовлетворяющее начальному условию y(1)=e. Выполнить проверку.

Решение

Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:

Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:

можно выразить функцию в явном виде.

Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.

Подставляем найденное значение константы C=1 в общее решение.

Ответ

Проверка

Необходимо проверить, выполняется ли начальное условие:

Из равенства выше видно, что начальное условие y(1)=e выполнено.

Далее проводим следующую проверку: удовлетворяет ли вообще частное решение

дифференциальному уравнению. Для этого находим производную:

Подставим полученное частное решение

и найденную производную в исходное уравнение

Получено верное равенство, значит, решение найдено правильно.

Задание

Найти общий интеграл уравнения

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Ответ

Задание

Найти частное решение ДУ.

Решение

Данное ДУ допускает разделение переменных. Разделяем переменные:

Найдем частное решение (частный интеграл), соответствующий заданному начальному условию

Подставляем в общее решение

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:

Левую часть интегрируем по частям:

В интеграле правой части проведем замену:

(здесь дробь раскладывается методом неопределенных коэффициентов)

Ответ

Задание

Решить дифференциальное уравнение

Решение

Данное уравнение допускает разделение переменных.

Разделяем переменные и интегрируем:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей: