Урок тригонометрии «Различные способы решения уравнения sinx + cosx = 1»
Разделы: Математика
Образовательные, развивающие и воспитательные цели урока:
Техническая оснащенность урока: компьютеры.
План сдвоенного урока.
I. Повторение по теме “Уравнения”.
Вопросы для повторения.
II. Сообщение темы урока, знакомство с целями.
Урок посвящён способам решения уравнения sin x + cos x = 1.
III. Ход работы.
Я буду ставить перед вами задачу, определив способ решения, а вы будете именно этим способом решать данное уравнение, используя различные приёмы. Работать будете на листочках. Кто раньше решит, выйдет и приведёт своё решение на обороте доски (такую возможность будут иметь одновременно 4 ученика).
По окончанию работы и сдачи листочков на проверку класс обсудит приведённые на доске варианты решений. Затем начнётся следующий этап работы. Не забывайте каждый раз подписывать листочки.
Различные способы решения тригонометрического уравнения sin x + cos x = 1.
I способ. Введение вспомогательного угла.
Рассмотрим два приёма:
Разделим обе части уравнения на 
Воспользуемся алгоритмом решения уравнений вида а sin x + b cos x = c.

Подпишите листочки.
- Изложите на листочках алгоритм использования вспомогательного угла при решении уравнений вида a sin x + b cos x =0.
- Запишите формулу применения синуса дополнительного угла для выражения sin x + cos x.
- Теперь выразите sin x + cos x через косинус дополнительного угла.
- Кто раньше закончит работу, покажет свои варианты ответов на доске.
II способ. С помощью универсальной тригонометрической подстановки.
Запишите формулы универсальной подстановки для sin x, cos x . Кто первый закончит, покажет на доске.

Выводы: Обращение к функции tgx / 2 предполагает, что cosx / 2 



При таком переходе возможна потеря решений, т.к. исходное уравнение имело смысл при всех значениях переменной х, в том числе и при x = 


Есть вероятность того, что они могут оказаться корнями исходного уравнения,
поэтому надо проверить, не являются ли значения x = 


sin ( 



-1 
Следовательно, x = 


Решением уравнения не является и переход к функции tgx / 2, в данном случае потери решения за собой не повлечёт. Итак, по формулам (1) из исходного уравнения sin x + cos x = 1, получаем:
III способ. Сведение к однородному уравнению.
Возможно, ли получить из данного уравнения однородное уравнение?
Надо перейти к аргументу x/2 и применить формулы половинного аргумента к функциям в левой и правой частях уравнения sin x + cos x = 1.
Написать на листочках формулы, которые при этом используются, и то однородное уравнение, которое получится. Получили однородное уравнение второй степени.
2sinx/2*cosx/2 + cos 2 x/2- sin 2 x/2 = sin 2 x/2 + cos 2 x/2 (2)
Подпишите листочки и решите данное однородное тригонометрическое уравнение второй степени
2sinx/2*cosx/2 + cos 2 x/2- sin 2 x/2 = sin 2 x/2 + cos 2 x/2,
2sinx/2*cosx/2 + cos 2 x/2- sin 2 x/2 — sin 2 x/2 — cos 2 x/2 = 0
sinx/2*cosx/2 — sin 2 x/2 = 0
Это уравнение можно решить, используя различные приёмы.
Разделим обе части уравнения на cos 2 x/2, т.к. cos 2 x/2 





Рассмотрим решение уравнения (2) способом разложения на множители:
sinx/2*cosx/2 — sin 2 x/2 = 0,
sinx/2*(cosx/2 — sinx/2) = 0,
x = 2

b) cosx/2 – sinx/2 = 0
x = 


Ответ : <2



IV способ. Преобразование суммы в произведение.
Запишите формулы преобразования суммы и разности тригонометрических функций в произведение. Кто первый закончит работу, воспроизведёт её на доске. Используя формулы преобразования суммы тригонометрических функций в произведение, решить данное уравнение:
а) Выразим cos x через sin(
О т в е т : <2



sin x + cos x = 1
б) Выразим sin x через cos (
V способ. Применение формул половинного и двойного аргумента.
Напишите формулы тригонометрических функций двойного аргумента и половинного аргумента.
Запишите: sin x + cos x = 1; sin x = 1- cos x, приведите левую и правую части уравнения к аргументу х/2, используя формулы двойного и половинного угла, и решите получившееся уравнение.
2sinx/2 * cosx/2 = 2 sin 2 x/2 ,
sinx/2 * cosx/2 = sin 2 x/2 ,
x = 


x = 2

Ответ: <2



Или это уравнение можно решить делением обеих частей на cos 2 x/2.
VI способ. Возведение обеих частей уравнения в квадрат:
sin x + cos x = 1,
(sin x + cos x) 2 = 1,
2 sin x cos x + 1= 1,
2 sin x cos x = 0,
При возведении в степень возможно появление посторонних решений уравнения, но не возможна потеря корней, т.е. получается уравнение-следствие. Причина приобретения корней состоит в том, что при возведении в квадрат чисел, равных по абсолютной величине, но разных по знаку, получается один и тот же результат.
При возведении в квадрат обеих частей уравнения sin x + cos x = 1, мы производим эту же операцию и с частями «теневого» уравнения (- sin x — cos x = 1), поскольку результат этих действий будет один и тот же.
Следовательно, по окончании решения, обязательно следует производить отбор корней.
1. Проверим корни вида x = 
Значит, значения x = 2

х= 

следовательно, значения x = 2

2. Проверяем корни вида x = 


j = 2n : x = 


Значит, значения x = 


x = 


следовательно, значения x = 


Ответ : <2



VII способ. Замена cos x выражением 
Проверив результат, убеждаемся, что из серии x = 



Ответ : <2



VIII способ. Графическое решение уравнения sin x + cos x = 1.
Предварительно проводится фронтальная беседа.
1. Что значит решить уравнение графически?
2. Как можно решить графически данное уравнение?
1. Построить в одной системе координат графики функций:
Абсциссы точек пересечения графиков функций и являются решением данного уравнения.
2. Построить график функции y = sin x+ cos x –1.
Абсциссы точек пересечения графика с осью абсцисс являются решением исходного уравнения.
3. Построение графиков на экране компьютера:
Прежде чем приступить к работе на компьютере, повторим элементы компьютерной грамотности, позволяющие построение графиков.
Что такое масштаб применительно к ЭВМ?
Масштаб – количество точек на экране, приходящееся на единицу значения.
Что называется пикселем?
Пиксель – наименьший объект графической среды, характеризующийся координатой Х и У (это точка на экране).
С помощью какого оператора можно построить точку на экране?
C помощью, какого оператора устанавливается новая система координат?
Window (x1, y1) – (x2, y2).
Рассказать о порядке построения линий осей координат на экране.
Line (x, y) – (x2, y2), c
Назовите операторы, которые обеспечивают надписи на осях координат.
Locate x, y: PRINT «Y».
Что собой представляет график на экране?
Что обеспечивает развёртку графика по осям координат?
Выполняем решение систем (1) на компьютере по соответствующим программам.
IV. Домашнее задание:
Решить различными способами уравнение sinx – cosx = 1 или любое другое уравнение.
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение тригонометрических уравнений.
Этот математический калькулятор онлайн поможет вам решить тригонометрическое уравнение. Программа для решения тригонометрического уравнения не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс получения ответа.
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите тригонометрическое уравнение
Решить уравнение
Немного теории.
Тригонометрические уравнения
Уравнение cos(х) = а
Из определения косинуса следует, что \( -1 \leqslant \cos \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение cos x = a не имеет корней. Например, уравнение cos х = -1,5 не имеет корней.
Уравнение cos x = а, где \( |a| \leqslant 1 \), имеет на отрезке \( 0 \leqslant x \leqslant \pi \) только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если a
Уравнение sin(х) = а
Из определения синуса следует, что \( -1 \leqslant \sin \alpha \leqslant 1 \). Поэтому если |a| > 1, то уравнение sin x = а не имеет корней. Например, уравнение sin x = 2 не имеет корней.
Уравнение sin х = а, где \( |a| \leqslant 1 \), на отрезке \( \left[ -\frac<\pi><2>; \; \frac<\pi> <2>\right] \) имеет только один корень. Если \( a \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right] \); если а
Уравнение tg(х) = а
Из определения тангенса следует, что tg x может принимать любое действительное значение. Поэтому уравнение tg x = а имеет корни при любом значении а.
Уравнение tg x = а для любого a имеет на интервале \( \left( -\frac<\pi><2>; \; \frac<\pi> <2>\right) \) только один корень. Если \( |a| \geqslant 0 \), то корень заключён в промежутке \( \left[ 0; \; \frac<\pi> <2>\right) \); если а
Решение тригонометрических уравнений
Выше были выведены формулы корней простейших тригонометрических уравнений sin(x) = a, cos(x) = а, tg(x) = а. К этим уравнеииям сводятся другие тригонометрические уравнения. Для решения большинства таких уравнений требуется применение различных формул и преобразований тригонометрических выражений. Рассмотрим некоторые примеры решения тригонометрических уравнений.
Уравнения, сводящиеся к квадратным
Решить уравнение 2 cos 2 (х) — 5 sin(х) + 1 = 0
Заменяя cos 2 (х) на 1 — sin 2 (х), получаем
2 (1 — sin 2 (х)) — 5 sin(х) + 1 = 0, или
2 sin 2 (х) + 5 sin(х) — 3 = 0.
Обозначая sin(х) = у, получаем 2у 2 + 5y — 3 = 0, откуда y1 = -3, y2 = 0,5
1) sin(х) = — 3 — уравнение не имеет корней, так как |-3| > 1;
2) sin(х) = 0,5; \( x = (-1)^n \text
Ответ \( x = (-1)^n \frac<\pi> <6>+ \pi n, \; n \in \mathbb
Решить уравнение 2 cos 2 (6х) + 8 sin(3х) cos(3x) — 4 = 0
Используя формулы
sin 2 (6x) + cos 2 (6x) = 1, sin(6х) = 2 sin(3x) cos(3x)
преобразуем уравнение:
3 (1 — sin 2 (6х)) + 4 sin(6х) — 4 = 0 => 3 sin 2 (6х) — 4 sin(6x) + 1 = 0
Обозначим sin 6x = y, получим уравнение
3y 2 — 4y +1 =0, откуда y1 = 1, y2 = 1/3
Уравнение вида a sin(x) + b cos(x) = c
Решить уравнение 2 sin(x) + cos(x) — 2 = 0
Используя формулы \( \sin(x) = 2\sin\frac
Поделив это уравнение на \( \cos^2 \frac
Обозначая \( \text
В общем случае уравнения вида a sin(x) + b cos(x) = c, при условиях \( a \neq 0, \; b \neq 0, \; c \neq 0, \; c^2 \leqslant b^2+c^2 \) можно решить методом введения вспомогательного угла.
Разделим обе части этого уравнения на \( \sqrt
Решить уравнение 4 sin(x) + 3 cos(x) = 5
Здесь a = 4, b = 3, \( \sqrt
Уравнения, решаемые разложением левой части на множители
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются разложением их левой части на множители.
Решить уравнение sin(2х) — sin(x) = 0
Используя формулу синуса двойного аргумента, запишем уравнепие в виде 2 sin(x) cos(x) — sin(x) = 0. Вынося общий множитель sin(x) за скобки, получаем sin(x) (2 cos x — 1) = 0
Решить уравнение cos(3х) cos(x) = cos(2x)
cos(2х) = cos (3х — х) = cos(3х) cos(x) + sin(3х) sin(x), поэтому уравнение примет вид sin(x) sin(3х) = 0
Решить уравнение 6 sin 2 (x) + 2 sin 2 (2x) = 5
Выразим sin 2 (x) через cos(2x)
Так как cos(2x) = cos 2 (x) — sin 2 (x), то
cos(2x) = 1 — sin 2 (x) — sin 2 (x), cos(2x) = 1 — 2 sin 2 (x), откуда
sin 2 (x) = 1/2 (1 — cos(2x))
Поэтому исходное уравнение можно записать так:
3(1 — cos(2x)) + 2 (1 — cos 2 (2х)) = 5
2 cos 2 (2х) + 3 cos(2х) = 0
cos(2х) (2 cos(2x) + 3) = 0
Решение тригонометрических уравнений графически
Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.
Пусть, например, нужно решить уравнение
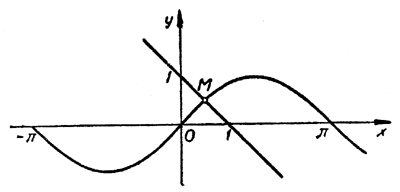
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х
Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:
Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5
следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x0 должен быть меньше, чем 0,6. Теперь уже мы знаем, что x0 находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1
С помощью таблиц можно найти приближенное значение x0 и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала
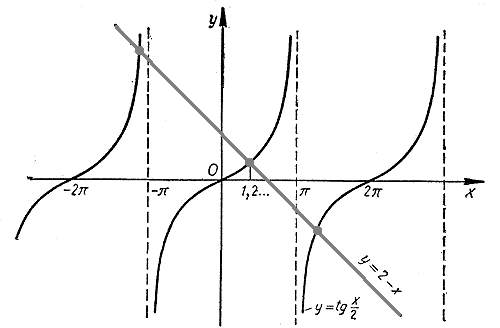
Графики функций у = tg x /2 и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х0. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.
Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /2 и у = 2 — х в окрестности точки х = 1,2.
| x | 1,2 | 1,3 |
| y=tg x/2 | 0,6841 | 0,7602 |
| y=2-x | 0,8000 | 0,7000 |
| tg x/2-(2-x) | -0,1159 | 0,0602 |
Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /2 — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х0 ≈ 1,2 (с недостатком) или х0 ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25
http://www.math-solution.ru/math-task/trigonometry-equality
http://razdupli.ru/teor/77_reshenie-trigonometricheskih-uravnenij-graficheski.php