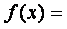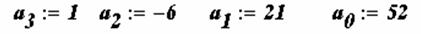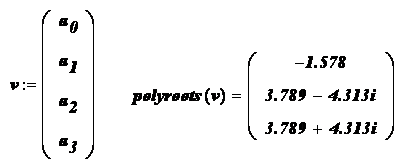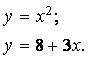Как решить нелинейное уравнение в маткаде

Решение нелинейных уравнений и систем уравнений в пакете MathCAD

Решение нелинейных уравнений

Вычисление корней численными методами включает два основных этапа:

· уточнение корней до заданной точности.

Рассмотрим эти два этапа подробно.

Отделение корней нелинейного уравнения

Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.

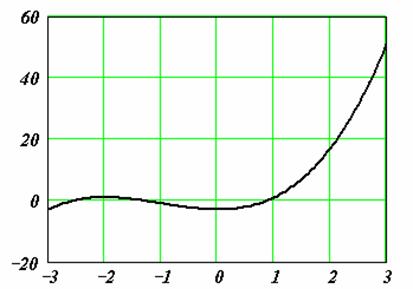
Пример. Дано алгебраическое уравнение

.

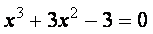
Определить интервалы локализации корней этого уравнения.

Пример. Дано алгебраическое уравнение

.

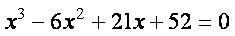
Определить интервалы локализации корней этого уравнения.

На рисунке приведен график функции 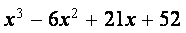, построенный в MathCAD . Видно, что в качестве интервала изоляции можно принять интервал . Однако уравнение имеет три корня. Следовательно, можно сделать вывод о наличии еще двух комплексных корней. ¨

Уточнение корней нелинейного уравнения

Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.

Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. или , где – имя функции или арифметическое выражение, соответствующее решаемому нелинейному уравнению, – скалярная переменная, относительно которой решается уравнение, – границы интервала локализации корня.

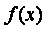
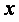
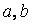
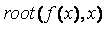
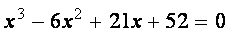
Пример. Используя функцию , найти все три корня уравнения , включая и два комплексных.

Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨

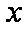
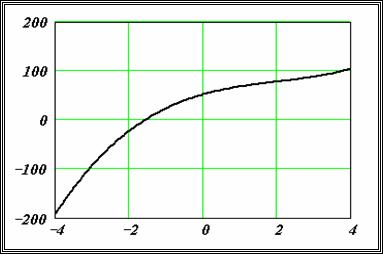
Функция root с двумя аргументами требует задания (до обращения к функции) переменной начального значения корня из интервала локализации.

Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения при изменении коэффициента а от 1 до 10 с шагом 1.

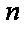
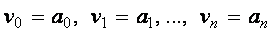
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка (не выше 5) рекомендуется использовать функцию polyroots . Обращение к этой функции имеет вид polyroots (v) , где v – вектор, состоящий из n +1 проекций, равных коэффициентам алгебраического уравнения, т.е. . Эта функция не требует проведения процедуры локализации корней.

Пример. Используя функцию polyroots , найти все три корня уравнения 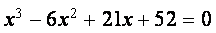, включая и два комплексных

Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:

Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логичес­кий .

Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.

Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.

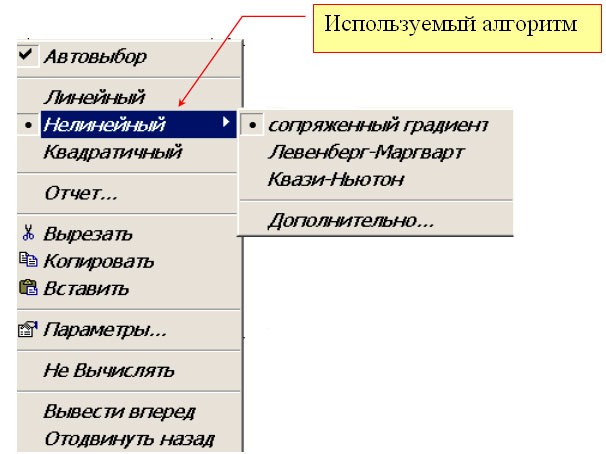
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.

Аналогично можно задать алгоритм решения и для функции Minerr ( x ).

Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.

Пример. Используя блок Given , вычислите корень уравнения 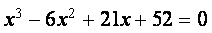в интервале отделения .

Решение систем уравнений

В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:

· алгебраические системы уравнений;

· трансцендентные системы уравнений.

Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).

Системы линейных алгебраических уравнений

Системой линейных алгебраических уравнений (СЛАУ) называется система вида:

В матричном виде систему можно записать как

,

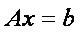
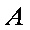
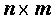
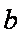
где – матрица размерности , – вектор с проекциями.

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 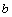– вектор правой части.

Решение систем нелинейных уравнений

MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.

Для решения системы уравнений необходимо выполнить следующие этапы.

Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.

Пример. Дана система уравнений:

Определить начальные приближения для решений этой системы.

Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨

Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .

Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.

Следующие выражения недопустимы внутри блока решения:

· ограничения со знаком ¹ ;

· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;

· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).

Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.

Пример. Используя функцию 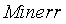, вычислите решение системы уравнений

MathCAD — это просто! Часть 5. Системы нелинейных уравнений

Добрый день, уважаемые читатели и читательницы, мы с вами продолжаем грызть гранит науки. Делаем мы это с целью — напомню, если кто вдруг успел позабыть — овладеть замечательным математическим пакетом под названием MathCAD. И в прошлый раз мы с вами закончили на решении систем линейных алгебраических уравнений, для простоты также обозначаемых как СЛАУ. Что ж, линейные уравнения — это, конечно же, спору нет, замечательно. Однако на них, к величайшему сожалению многих поколений школьников и студентов, математические задачи далеко не заканчиваются, а даже, я бы сказал, напротив. То есть СЛАУ — это только частный случай систем уравнений, которые могут в обыкновенной вычислительной практике оказаться совсем даже и не линейными, а, напротив, нелинейными (да, именно так их и называют математики). Системы нелинейных уравнений без использования MathCAD или какого-либо другого математического пакета решать обычно не просто трудно, а очень трудно, но в MathCAD подход к ним не слишком отличается от подхода к СЛАУ — в этом вы сейчас получите возможность убедиться лично.

В общем-то, основные аспекты аналитического решения систем уравнений мы с вами уже, по большому счету, обсудили. Когда это мы так лихо успели? А вот именно тогда, когда обсуждали аналитическое решение систем линейных уравнений с помощью оператора solve. Оказывается, все те же методы вполне применимы для решения систем нелинейных уравнений. Тем не менее, чтобы вы лучше их усвоили, повторю еще раз кратко алгоритм их решения с помощью MathCAD’а и приведу небольшой пример решения подобной системы. Давайте попробуем решить следующую систему уравнений: ex + y + z(xyz)1/2 = 0
(x + y+ z)1/2 = c
x +y + cz = 0

Система выглядит несложной, но для того, чтобы решить ее без использования MathCAD’а, даже очень хорошему математику потребуется не такое уж малое количество времени. Естественно, MathCAD с этой системой справится в два счета. Для ее решения создайте матрицу размером 3 на 1 (3 строки, 1 столбец), в которую и поместите уравнения нашей системы. Напомню, что для того, чтобы MathCAD распознавал уравнения как уравнения, знак «равно» нужно нажимать, удерживая клавишу Ctrl. После того, как система будет введена в виде матрицы, найдите на панели Symbolic оператор solve — мы им уже неоднократно пользовались для решения и простых уравнений, и СЛАУ, так что вы, по идее, уже должны были запомнить, где именно он находится. После оператора через запятые укажите переменные, которые входят в нашу систему уравнений — это пусть будут для начала x, y и z. Поскольку при вводе solve с панели Symbolic MathCAD сам добавляет нужную стрелочку для аналитического решения нашей с вами системы уравнений, то больше ничего, в общем-то, делать не нужно — дальше MathCAD будет решать систему. Сколько это времени у него займет, зависит, конечно же, от мощности вашего компьютера, ну и от самой системы. Нашу систему он решит быстро, а вот если поизвращаться и написать какую-нибудь систему тригонометрических и логарифмических уравнений, да еще и с комплексными переменными (о них мы потом еще поговорим отдельно), то решать такое MathCAD может на слабых компьютерах и не один час.

Для чистоты эксперимента поменяем переменные: пусть теперь произвольной константой в нашей системе будет не c, а z. В этом случае нас ожидает совершенно другое, куда как более громоздкое, решение этой самой системы.

Как видите, аналитическое решение систем нелинейных уравнений с помощью MathCAD’а — вещь несложная, только, к сожалению, возможная далеко не всегда. Как обычно, на помощь символьному процессору MathCAD, который опускает в бессилии руки перед сложными системами, спешат численные методы. Вот здесь уже начинаются различия с системами линейных уравнений.

Численное решение нелинейных систем

В целом алгоритм решения систем нелинейных уравнений в MathCAD для пользователя мало чем отличается от него же для СЛАУ. Мы точно так же задаем начальные приближения, пишем «Given», записываем под этим словом наши уравнения и запрягаем функцию Find, которая должна вывести эти самые уравнения на чистую воду. Все точно так же, как тогда, когда мы решали СЛАУ.

Почему же я так пугал вас буквально двумя абзацами выше, говоря о том, что решать системы нелинейных уравнений намного сложнее, чем СЛАУ? Дело в том, что в случае нелинейных уравнений намного сложнее подобрать такие начальные значения, чтобы численное решение сходилось к реальным значениям корней уравнений. Честно говоря, со СЛАУ тоже не всегда все так просто, как я в прошлый раз сказал, однако в крайнем случае можно заставить MathCAD решить СЛАУ аналитически, а затем просто подставить конкретное численное значение какого-нибудь коэффициента. С нелинейными системами такой прием, что называется, «не покатит». Именно поэтому для получения максимального точного решения многих из таких систем придется озадачиться такими вещами, как задание начальных значений для наших переменных.

Первый способ, который я вам предложу, сразу предупреждаю, для людей неленивых. Заключается он в банальном подборе значений переменных собственными руками. То есть для начала берем начальные значения «с потолка» и решаем систему с помощью Find’а. Подставляем значения, выданные этой функцией, в исходные уравнения и смотрим, насколько они похожи на истинные решения. Если уравнения обращаются при подстановке в верные равенства, то все хорошо: либо система была простой, либо в вас дремлет талант подбирателя корней уравнений. Но если равенством после подстановки и близко не пахнет, то придется попотеть. Нужно начать изменять значения начальных приближений для каждой переменной и смотреть, как это отразится на близости выражений, получившихся после подстановки решений в уравнения, к равенствам. Таким нехитрым методом можно за не столь долгое время, как может сначала показаться, добиться хорошего приближения начальных значений к реальным решениям. И, несмотря на явный садомазохистский характер данного метода, он имеет то неоспоримое преимущество, что действует железно на любые системы и любые переменные — было бы терпение.

Второй метод, который я хочу предложить, этим достоинством не обладает, но зато и не требует от пользователя столь деятельного участия в решении. Думаю, вы сами сможете сформулировать главный его недостаток, если я скажу, что с этим методом мы уже сталкивались, и заключается он в построении графиков для уравнений, входящих в систему. Да, главный недостаток — это сложность в применении к системам уравнений, содержащим более трех переменных. Сложно, сами понимаете, изобразить на мониторе компьютера 25-мерное пространство для отображения решений системы с 25-ю переменными. Но для тех систем, которые содержат две или три переменные, построить график мы вполне сможем. Однако для этого сначала нужно научиться строить графики уравнений.

Построение графиков параметрических кривых

Наиболее простым способом построения графика уравнения в MathCAD’е является параметризация входящих в него переменных друг через друга или через какую-то третью переменную. Что это означает? Поясню на примере. Например, у нас есть уравнение окружности x2 + y2 = 5. Если вы попытаетесь записать функцию f(x, y) = x2 + y2 — 5, а потом построить ее график от x или от y, то вас ожидает разочарование. То, что в итоге выдаст на экран MathCAD, будет так же мало похоже на окружность, как сам MathCAD — на пасьянс «Косынка». Придется придумывать что-то другое. Например, можно подобрать такие функции переменной t, которые, будучи возведенными в квадрат, в сумме тоже дадут пять. Естественно, такими функциями будут тригонометрические — синус и косинус от переменной t, помноженные на корень из пяти. Если мы выразим таким образом x и y через t, то мы параметризуем наше уравнение и уже сможем успешно построить график x(t) от y(t) или же y(t) от x(t) — впрочем, в данном случае в силу симметричности это будет уже не столь важно.

Для того, чтобы решить систему уравнений, нужно просто подобным образом параметризовать и второе уравнение. Вполне возможно, что, как и в нашем примере, оно вполне подойдет для того, чтобы банально выразить x через y или наоборот, после чего построение графика окажется особенно простым (см. соответствующий скриншот). Для нахождения начальных приближений достаточно воспользоваться уже знакомой нам с вами трассировкой — само собой, решением будет точка пересечения двух кривых на уравнении. Для того, чтобы получить более точное значение решения, чем предлагает нам трассировка, нужно, конечно же, подставить полученные с ее помощью координаты точки пересечения графиков в численное решение системы перед Given’ом. Последний скриншот иллюстрирует, что графики мы с вами построили правильно, и с его помощью действительно намного легче искать решение системы двух исходных уравнений. А легче хотя бы уже просто потому, что видно, какого количества корней мы вправе ожидать от нашей системы.

Но работа с трехмерными графиками в MathCAD’е не так проста, как с двумерными, поскольку и сама по себе поверхность — более сложный объект, чем кривая. С поверхностями можно ожидать немалого количества не самого приятного рода сюрпризов, так что лучше о них поговорить более подробно. Этим мы с вами и займемся в следующей статье из цикла о MathCAD’е.

Компьютерная газета. Статья была опубликована в номере 17 за 2008 год в рубрике soft

Нелинейные уравнения в MathСad

Mathcad отменно справляется с обчислениями нелинейных уравнений благодаря специальным алгоритмам.

Изучая решения, предлагаемые программой, попробуем стартовать с примера с одной переменной. Поэтому пытаемся возвести график для наглядности. Далее нам предстоит рассмотреть систему уравнения.

Уравнения с одной переменной

Сейчас мы попробуем решить максимально простой пример.

Учтем, что это уравнение представляет собой пересекающиеся параболу и прямую линию. Нарисуем график из трёх прямых линий и смотрим на результаты.

Верхняя линия имеет два пересечения с параболой. Обратите внимание на верхнюю линию. Запускаем блок решения для того, чтобы перейти к развязке уравнения.

На данном этапе появляются три части для ведения записи.

В область ограничения уже записано актуальное уравнение. Слева задано его приблизительное значение. Решателем является функция find.

Очевидно, что 1.366. Оно представляет собой первую стычку параболы и прямой линии.

Пробуем поменять изначальное приближение к обозначению, более близкому к пересечению с левой стороны. Решение автоматически принимает показатель в -0.366.

Начальное приближен снова устанавливаем на 1.3. Пробуем поменять константу 0.5 на -0.25. посмотрите, что стало с решением.

Примерно такой же ответ станет окончательным для абсолютно любого обозначения изначального приближения.

Теперь переходим в последнее уравнение и ставим константу на -1. Кликните по полю за пределами блока. Программа автоматически выдаст информацию о наличии ошибки.

Решения не существует. Ставим константу снова на 0.5.

Вывод решения

Решения, находящиеся в рассматриваемом нами блоке, являются локальными. Соответственно, их нельзя использовать за пределами блока. Теперь переходим к уравнению, в котором мы установили приближенное значение на отметке в 1.3. Решение данного уравнения помогает отыскать максимально точное значение х=1.366. Если же попытаться внести значение х, у нас отобразится вектор, который оптимально определится нашим графиком.

Чтобы пользоваться полученными данными в дальнейшем, понадобится установить функцию решателя переменной.

Так мы сможем получить правильный результат.

Решение систем уравнений

Попытаемся разобраться с системой из трёх уравнений. Два из них линейные, одно — кубическое. Соответственно у нас есть сразу три неизвестных.

Полученные ответы оформляем как векторы.

Удаляем третье уравнение. Его отсутствие не помешает системе найти правильный ответ.

Обратите внимание, что полученное решение может оказаться не тем, что вы искали.

Также вам понадобится учесть ещё некоторые особенности данных исчислений. Блок решения отображает сразу два знака равнения. Также там можно увидеть знак присваивания и символ булева равенства. Данная разница имеет колоссальную значимость. Теперь нажмите дважды по опции «find». Далее нам нужно открыть вкладку математики. В опции обозначения автоматически активировано «ключевое». Более подробную информацию о таких функциях мы расскажем в остальных уроках.

Растворимость вещества

Теперь посвятим время изучению процесса растворения такого вещества, как DOH. Этот процесс производится двумя этапами. Сначала нужно растворить твердую фазу. После этого оставшуюся часть нужно диссоциировать на D и OH. Невысокий уровень растворимости можно увеличить, подмешав немного кислоты НА. После этого ионы водорода начинают взаимодействовать с гидроксильной группой.

В чем же проявляется зависимость растворимости D от количества кислоты? Давайте посчитаем концентрацию в моль/л. Формула данной реакции выглядит таким образом:

Уровень концентрации кислоты:

Константа равновесия реакции:

Начало блока решения стартует с трех неизвестных и их первоначальных приближений:

Полученная концентрация вещества:

А так будет выглядеть расчет, предназначенный для возведения графика.

График наглядно отображает концентрирование в виде функцию с учетом количества добавленной кислоты. Концентрация водорода оказалась значительно ниже, чем концентрация иных элементов. С учетом этого фактора, мы приняли решение снизить масштабирование в 1000000 раз и отобразить данный график в этих же осях.

Когда концентрирование кислоты чрезмерно низко, в решении будет отображена минимальная концентрация, диссоциируемая лишь частично. Увеличив концентрацию, можно просмотреть за тем, как диссоциируется все больше вещества.

Уважаемые пользователи, хотим Вас проинформировать о том, что некоторые антивирусные программы и браузеры ложно срабатывают на дистрибутив программы MediaGet, считая его зараженным. Данный софт не содержит никаких вредоносных программ и вирусов и многие из антивирусов просто Вас предупреждают, что это загрузчик (Downloader). Если хотите избежать подобных проблем, просто добавьте MediaGet в список доверенных программ Вашей антивирусной программы или браузера.

Выбрав нужную версию программы и кликнув ссылку, Вам на компьютер скачивается дистрибутив приложения MediaGet, который будет находиться в папке «Загрузки» для Вашего браузера. Находим этот файл с именем программы и запускаем его. И видим первый этап установки. Нажимаем унопку «Далее»

Далее Вам предлагается прочитать и одобрить лицензионное соглашение. Нажимаем кнопку «Принимаю»

В следующем окне Вам предлагается бесплатное полезное дополнительное программоное обеспечение, будь то антивирус или бразуер. Нажимаем кнопку «Принимаю». Также Вы можете отказаться от установки дополнительного ПО, нажав кнопку «Отклоняю»

Далее происходит процесс установки программы. Вам нужно выбрать папку, в которую будут скачиваться нужные Вам файлы.

Происходит завершение установки. Программа автоматически открывается и скачивает нужные Вам исходные файлы.

Обратите внимание, что предоставляемое программное обеспечение выкладывается исключительно для личного использования и ознакомления. Все файлы, доступные для скачивания, не содержат вирусов и вредоносных программ.