Квадратные неравенства, примеры, решения
В данном разделе мы собрали информацию о квадратных неравенствах и основных подходах к их решению. Закрепим материал разбором примеров.
Что представляет собой квадратное неравенство
Давайте посмотрим, как по виду записи различать неравенства различных видов и выделять среди них квадратные.
Квадратное неравенство – это такое неравенство, которое имеет вид a · x 2 + b · x + c 0 , где a , b и c – некоторые числа, причем a не равно нулю. x – это переменная, а на месте знака может стоять любой другой знак неравенства.
Вторым названием квадратных уравнений является название «неравенства второй степени». Объяснить наличие второго названия можно следующим образом. В левой части неравенства находится многочлен второй степени – квадратный трехчлен. Применение к квадратным неравенствам термина «квадратичные неравенства» некорректен, так как квадратичными являются функции, которые задаются уравнениями вида y = a · x 2 + b · x + c .
Приведем пример квадратного неравенства:
Возьмем 5 · x 2 − 3 · x + 1 > 0 . В этом случае a = 5 , b = − 3 и c = 1 .
Или вот такое неравенство:
− 2 , 2 · z 2 − 0 , 5 · z − 11 ≤ 0 , где a = − 2 , 2 , b = − 0 , 5 и c = − 11 .
Покажем несколько примеров квадратных неравенств:
Здесь коэффициенты этого квадратного неравенства есть ; 1 2 3 · x 2 — x + 5 7 0 , в этом случае a = 1 2 3 , b = — 1 , c = 5 7 .
Особое внимание нужно обратить на тот факт, что коэффициент при x 2 считается неравным нулю. Объясняется это тем, что иначе мы получим линейное неравенство вида b · x + c > 0 , так как квадратная переменная при умножении на ноль сама станет равной нулю. При этом, коэффициенты b и c могут быть равны нулю как вместе, так и по отдельности.
Пример такого неравенства x 2 − 5 ≥ 0 .
Способы решения квадратных неравенств
Основным метода три:
- графический;
- метод интервалов;
- через выделение квадрата двучлена в левой части.
Графический метод
Метод предполагает проведение построения и анализа графика квадратичной функции y = a · x 2 + b · x + c для квадратных неравенств a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) . Решением квадратного неравенства являются промежутки или интервалы, на которых указанная функция принимает положительные и отрицательные значения.
Метод интервалов
Решить квадратное неравенство с одной переменной можно методом интервалов. Метод применим для решения любого вида неравенств, не только квадратных. Суть метода в том, чтобы определить знаки промежутков, на которые разбивается ось координат нулями трехчлена a · x 2 + b · x + c при их наличии.
Для неравенства a · x 2 + b · x + c 0 решениями являются промежутки со знаком минус, для неравенства a · x 2 + b · x + c > 0 , промежутки со знаком плюс. Если мы имеем дело с нестрогими неравенствами, то решением становится интервал, который включает точки, которые соответствуют нулям трехчлена.
Выделение квадрата двучлена
Принцип выделения квадрата двучлена в левой части квадратного неравенства состоит в выполнении равносильных преобразований, которые позволяют перейти к решению равносильного неравенства вида ( x − p ) 2 q ( ≤ , > , ≥ ) , где p и q – некоторые числа.
Неравенства, сводящиеся к квадратным
К квадратным неравенствам с помощью равносильных преобразований можно прийти от неравенств других видов. Сделать это можно разными способами. Например, перестановкой в данном неравенства слагаемых или переносом слагаемых из одной части в другую.
Приведем пример. Рассмотрим равносильное преобразование неравенства 5 ≤ 2 · x − 3 · x 2 . Если мы перенесем все слагаемые из правой части в левую, то получим квадратное неравенство вида 3 · x 2 − 2 · x + 5 ≤ 0 .
Необходимо найти множество решений неравенства 3 · ( x − 1 ) · ( x + 1 ) ( x − 2 ) 2 + x 2 + 5 .
Решение
Для решения задачи используем формулы сокращенного умножения. Для этого соберем все слагаемые в левой части неравенства, раскроем скобки и приведем подобные слагаемые:
3 · ( x − 1 ) · ( x + 1 ) − ( x − 2 ) 2 − x 2 − 5 0 , 3 · ( x 2 − 1 ) − ( x 2 − 4 · x + 4 ) − x 2 − 5 0 , 3 · x 2 − 3 − x 2 + 4 · x − 4 − x 2 − 5 0 , x 2 + 4 · x − 12 0 .
Мы получили равносильное квадратное неравенство, которое можно решить графическим способом, определив дискриминант и точки пересечения.
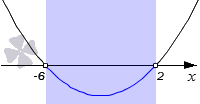
D ’ = 2 2 − 1 · ( − 12 ) = 16 , x 1 = − 6 , x 2 = 2
Построив график, мы можем увидеть, что множеством решений является интервал ( − 6 , 2 ) .
Ответ: ( − 6 , 2 ) .
Примером неравенств, которые часто сводятся к квадратным, могут служить иррациональные и логарифмические неравенства. Так, например, неравенство 2 · x 2 + 5 x 2 + 6 · x + 14
равносильно квадратному неравенству x 2 − 6 · x − 9 0 , а логарифмическое неравенство log 3 ( x 2 + x + 7 ) ≥ 2 – неравенству x 2 + x − 2 ≥ 0 .
Квадратные неравенства
Чтобы решить квадратные неравенства вспомним, что такое квадратичная функция?
Квадратичная функция – это функция записанная формулой : y=ax 2 +bx+c, где x – независимая переменная, a, b и c – некоторые числа, при этом a≠0.
Графиком квадратичной функции является парабола.
В зависимости от значения a ветви графика направлены вверх или вниз:
- если a>0, то ветви параболы направлены вверх;
- если a 2 +bx+c=0
Квадратные неравенства имеют вид.
ax 2 +bx+c>0
ax 2 +bx+c 2 +bx+c≥0
ax 2 +bx+c≤0
Чтобы начать решать квадратные неравенства, необходимо знать как решаются квадратные уравнения?
А также для графического метода решения неравенства, необходимо знать алгоритм построения квадратичной функции или параболы?
Как решать квадратные неравенства?
Решение квадратных неравенств рассмотрим на примерах. Для начала разберем случаи, когда у квадратного уравнения дискриминант меньше нуля (нет корней).
Пример:
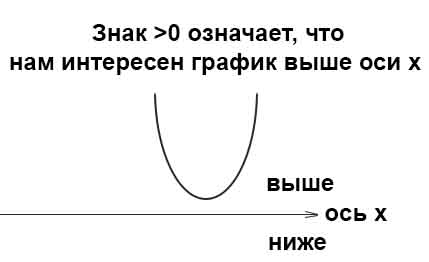
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, а это значит, что весь график параболы находится выше оси х, потому что а=3>0 (ветви параболы смотрят вверх)
Можно проверить себя взяв любое число с числовой прямой, например число 1. Подставить число 1 вместо переменой х в неравенство 3x 2 +2x+20>0.
Получили верное неравенство 25>0, следовательно так как у нас нет корней уравнения нам подойдут все точки числовой прямой.
Пример:
Рассмотрим этот же пример со знаком неравенства меньше 0
3x 2 +2x+20 2 +2x+20=0
Дискриминант меньше нуля —236, следовательно у уравнения нет корней, значит парабола не пересекает ось x. Весь график параболы находится выше оси х, потому что а=3>0.
А знак уравнения меньше 2 +2x+20 2 +2•1+20 2 +x-2 2 +x-2=0
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения меньше 2 +x-2 2 +(-3)-2 2 +(0)-2 2 +(2)-2 2 +x-2>0
Дискриминант больше нуля, следовательно у уравнения два корня, значит парабола пересекает ось x в точка x=1 и x=-2. Ветви параболы смотрят вверх, потому что а=1>0.
Знак уравнения больше >0. Нам в ответ необходимо записать часть параболы, которая находится выше оси x. Визуально графически можно оценить по картинке, нам подходят интервалы (-∞;-2) и (1;+∞).

Первый участок (-∞;-2). На этом участке можно взять любое число меньше -2, например возьмем число -3 и подставим в неравенство x 2 +x-2 2 +(-3)-2>0
Получили верное неравенство 4>0, следовательно этот интервал (-∞; 2) подходит.
Второй участок (-2; 1). На этом участке можно взять число 0.
Получили неверное неравенство -2>0, следовательно этот интервал (-2; 1) не подходит.
Третий участок (1; +∞). На этом участке возьмем число 2.
Получили верное неравенство 4>0, следовательно этот интервал (1; +∞) подходит.
Метод интервалов, решение неравенств
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax 2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
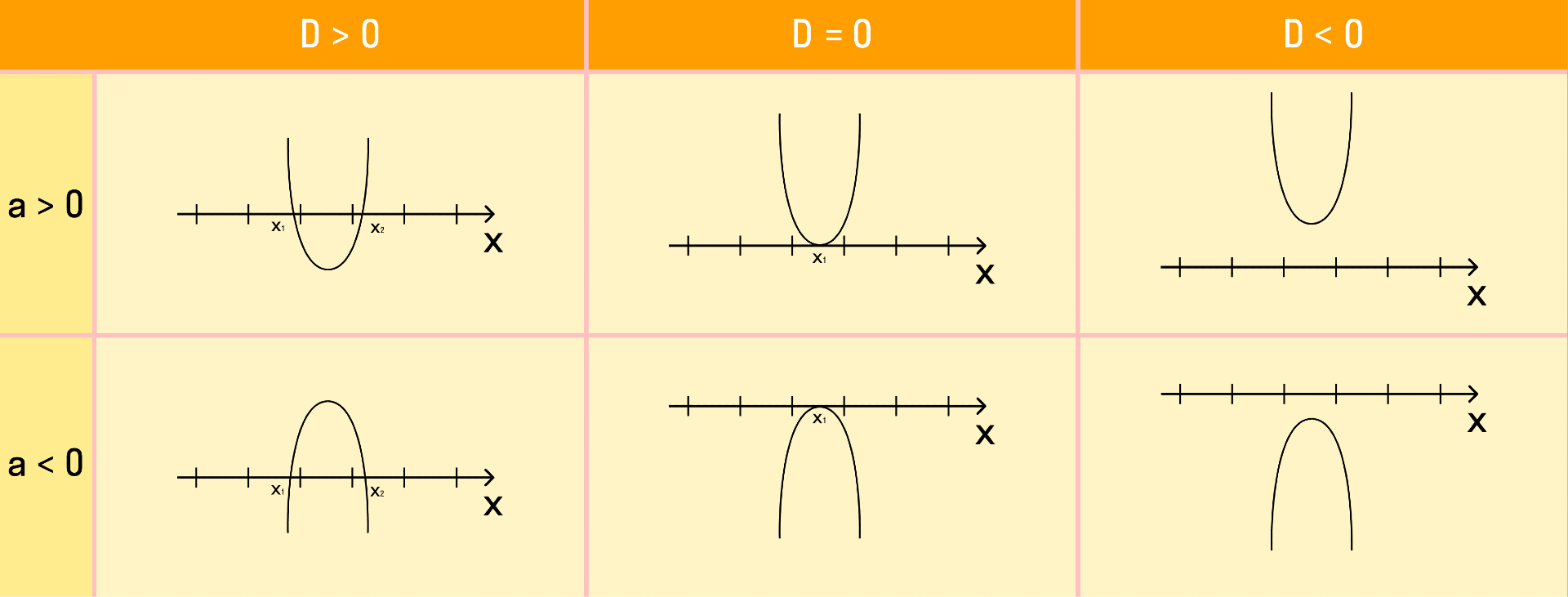
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два различных корня;
- D 2 + bx + c.
Если требуется найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.
Если нужно найти числовой промежуток, на котором квадратный трехчлен ax 2 + bx + c меньше нуля — это числовой промежуток, где парабола лежит ниже оси ОХ.
Если квадратное неравенство нестрогое, то корни входят в числовой промежуток. А если строгое — не входят.
Обучение на курсах по математике в онлайн-школе Skysmart сделает сложные темы понятными, а высокий балл на экзаменах — достижимым!
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, 2 + bx + c из левой части квадратного неравенства.
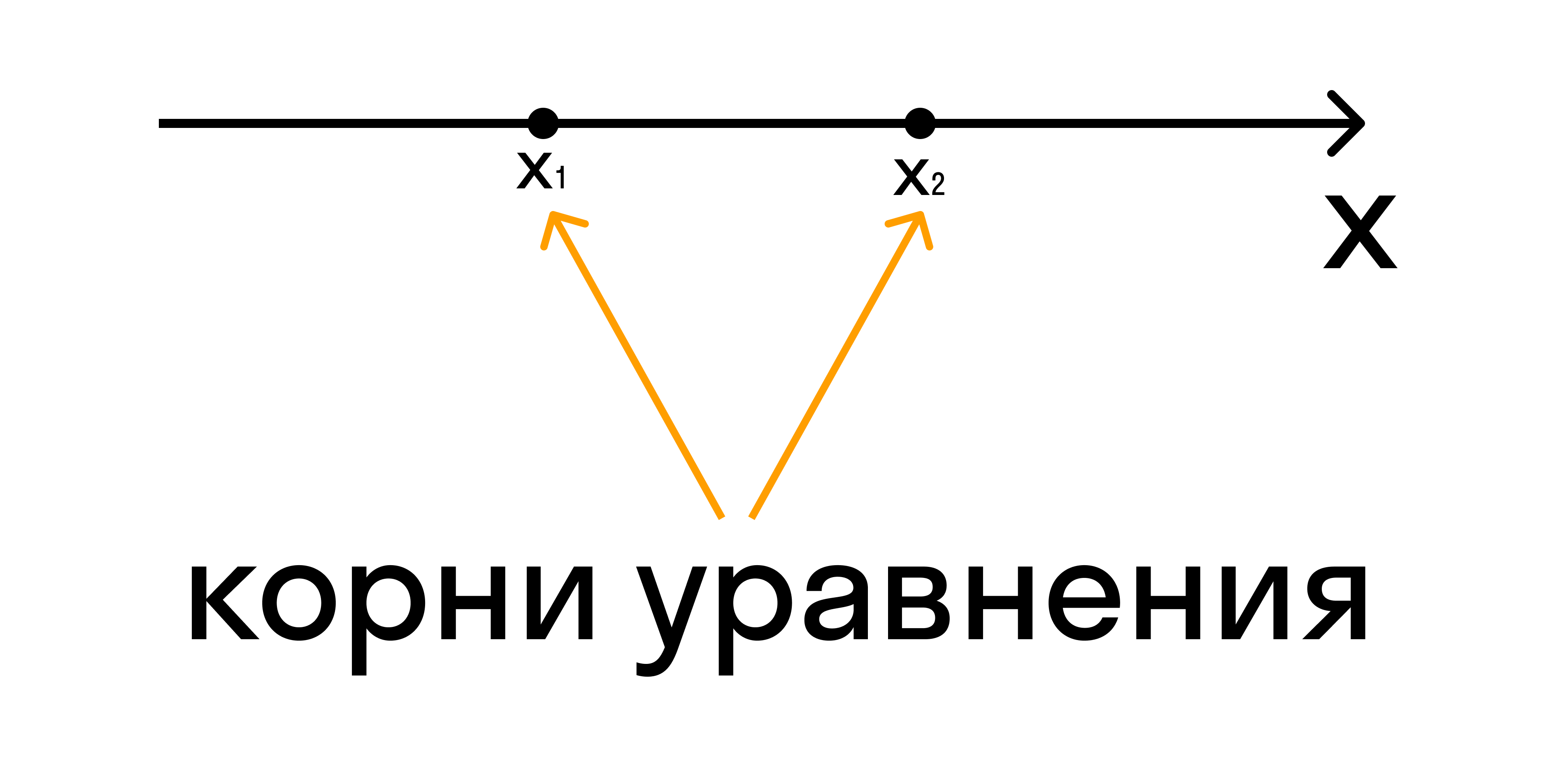
Изобразить координатную прямую и при наличии корней отметить их на ней.
Если неравенство строгое, нужно отметить корни пустыми (выколотыми) точками. Если нестрогое — обычными точками. Именно эти точки разбивают координатную ось на промежутки.
Если неравенство со знаком 2 + 4x — 5, его корнями являются числа -5 и 1, они разбивают числовую ось на три промежутка: (-∞, -5), (-5, 1) и (1, +∞).
Определим знак трехчлена x 2 + 4x — 5 на промежутке (1, +∞). Для этого вычислим значение данного трехчлена при некотором значении x из этого промежутка. Можно брать любое значение переменной, главное — чтобы вычисления были простыми. В нашем случае, возьмем x = 2. Подставим его в трехчлен вместо переменной x:
- 2 2 + 4 * 2 — 5 = 4 + 8 — 5 = 7.
7 — положительное число. Это значит, что любое значение квадратного трехчлена на интервале (1, +∞) будет положительным. Так мы определили знак плюс.
Определим знаки на оставшихся двух промежутках. Начнем с интервала (-5, 1). Из этого интервала можем взять x = 0 и вычислить значение квадратного трехчлена при этом значении переменной:
- 0 2 + 4 * 0 — 5 = 0 + 0 — 5 = -5.
Так как -5 — отрицательное число, то на этом интервале все значения трехчлена будут отрицательными. Так мы определили знак минус.
Осталось определиться со знаком на промежутке (-∞, -5). Возьмем x = -6, подставляем:
- (-6) 2 + 4 * (-6) — 5 = 36 — 24 — 5 = 7.
Следовательно, искомый знак — плюс.
Можно расставить знаки быстрее, если запомнить эти факты:
Плюс или минус: как определить знаки
Можно сделать вывод о знаках по значению старшего коэффициента a:
если a > 0, последовательность знаков: +, −, +,
если a 0, последовательность знаков: +, +,
если a 2 — 7 не имеет корней и на промежутке (−∞, +∞) его значения отрицательны, так как коэффициент при x 2 есть отрицательное число -4, и свободный член -7 тоже отрицателен.
- Когда квадратный трехчлен при D > 0 имеет два корня, то знаки его значений на промежутках чередуются. Это значит, что достаточно определить знак на одном из трех промежутков и расставить знаки над оставшимися промежутками, чередуя их. В результате возможна одна из двух последовательностей: +, −, + или −, +, −.
- Если квадратный трехчлен при D = 0 имеет один корень, то этот корень разбивает числовую ось на два промежутка, а знаки над ними будут одинаковыми. Это значит, что достаточно определить знак над одним из них и над другим поставить такой же. При этом получится, либо +, +, либо −, −.
- Когда квадратный трехчлен корней не имеет (D
Теперь мы знаем пошаговый алгоритм. Чтобы закрепить материал потренируемся на примерах и научимся использовать метод интервалов для квадратных неравенств.
Пример 1. Решить неравенство методом интервалов: x^2 — 5x + 6 ≥ 0.
Разложим квадратный трехчлен на множители.
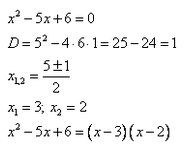
Неравенство примет вид:
Проанализируем два сомножителя:
Первый: х — 3. Этот сомножитель может поменять знак при х = 3, значит при х 0 принимает положительные значения: х — 3 > 0.
Второй: х — 2. Для этого сомножителя такая «знаковая» точка: х = 2.
Вывод: знак произведения (х — 3) * (х — 2) меняется только при переходе переменной через значения х = 3 и х = 2.
В этом весь смысл метода интервалов: определить интервалы значений переменной, на которых ситуация не меняется и рассматривать их как единое целое.
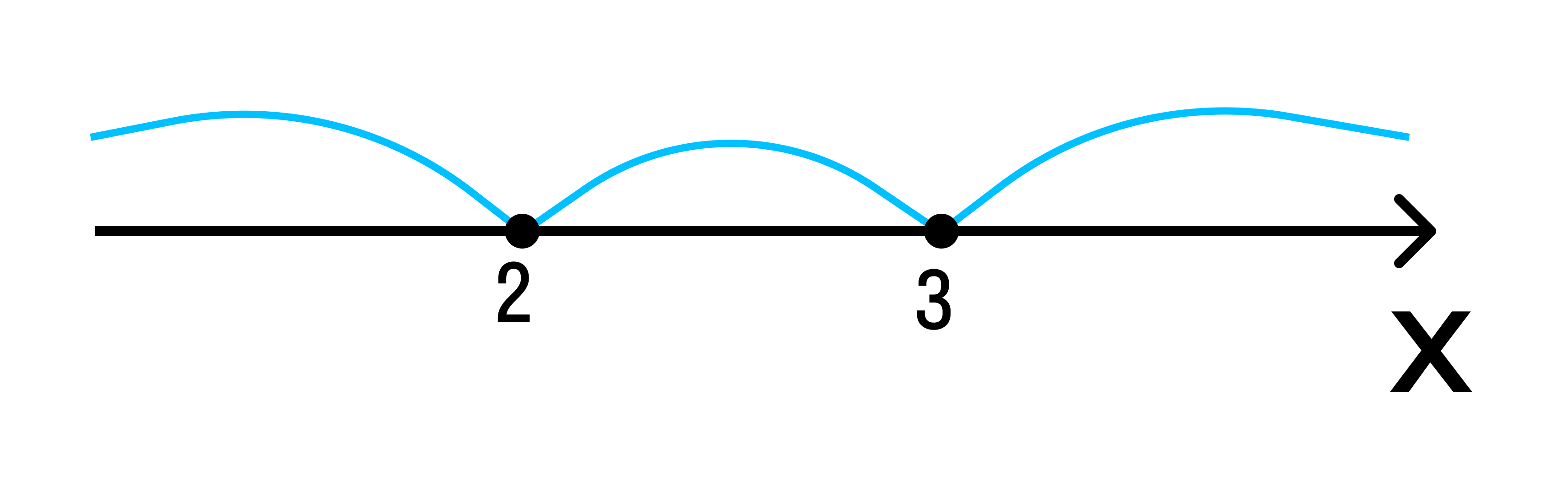
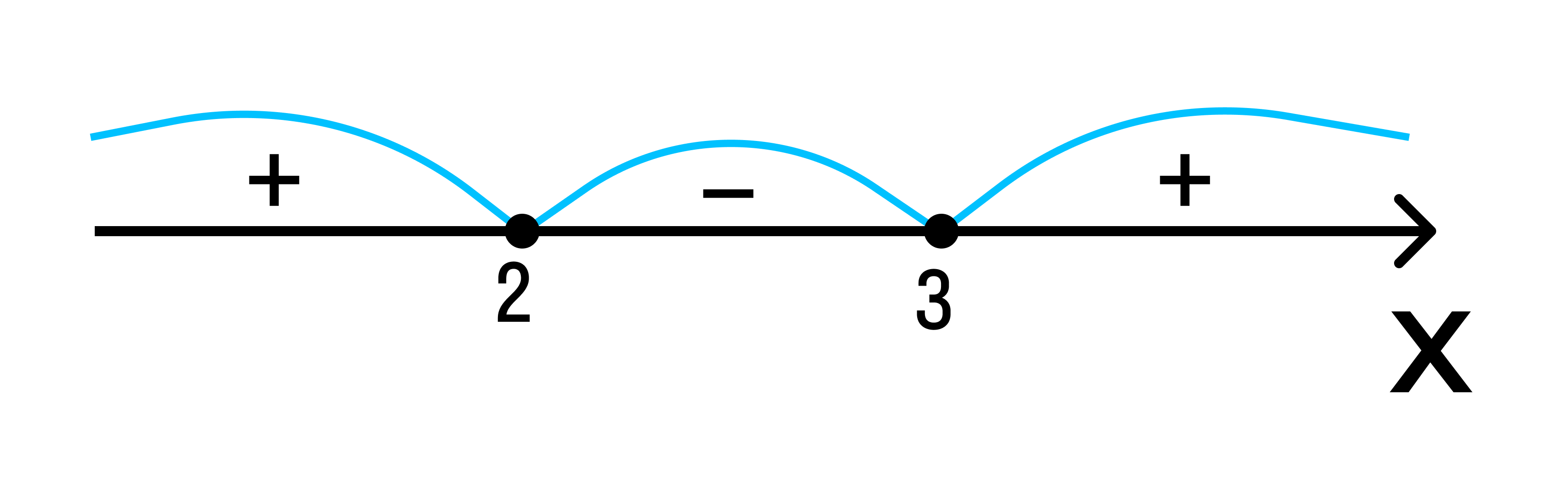
Отобразим эти данные на чертеже:
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.
Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
http://tutomath.ru/9-klass/kvadratnie-neravenstva.html
http://skysmart.ru/articles/mathematic/metod-intervalov-reshenie-neravenstv