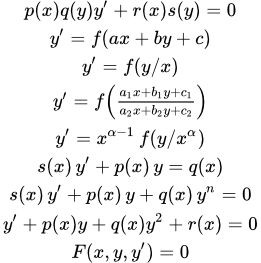Как решить разностное уравнение первого порядка

Решения разностных уравнений

Разностные уравнения для чайников

На этой странице мы рассмотрим примеры решения типовых задач, встречающихся в курсе дифференциальных и разностных уравнений, а именно нахождение общего или частного решения линейного разностного уравнения с постоянными коэффициентами. Чаще всего в контрольных встречаются уравнения второго или третьего порядка:

$$ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)=f(x), \\ a_0 y(x) + a_1 y(x+1) + a_2 y(x+2)+ a_3 y(x+3)=f(x). $$

Здесь $a_i$ — постоянные коэффициенты, $f(x)$ — правая часть (неоднородность уравнения), $y(x)$ — искомая неизвестная функция.

Решение разностных уравнений практически полностью аналогично решению линейных дифференциальных уравнений с постоянными коэффициентами (см. тут примеры): ищется решение однородного уравнения через составление характеристического уравнения, и частное решение неоднородного уравнения по виду правой части.

Примеры решений разностных уравнений

Задача 1. Решить разностное уравнение: $y(x+2)-4y(x+1)+4y(x)=2^x$

Задача 2. Найти общее решение линейного разностного неоднородного уравнения второго порядка с постоянными коэффициентами.

Задача 3. Решить разностное уравнение третьего порядка

$$ y(x+3)-16y(x+2)+83y(x+1)-140y(x)=0, \quad y(0)=3, y(1)=18, y(2)=120. $$

Задача 4. Найти частное решение однородного разностного уравнения:

Помощь с разностными уравнениями

Если вам нужна помощь с решением задач и контрольных по дифференциальным и разностным уравнениям (и другим разделам математического анализа), обращайтесь в МатБюро. Стоимость подробной консультации от 100 рублей , оформление производится в Word, срок от 1 дня.

Разностные уравнения

Содержание:

Разностные уравнения

Понятие разницы и разностного уравнения

Если для значений переменной x₁, x₂, x₃, . функция f (x) принимает значения f (x₁), f (x₂), f (x₃) . , то приращения функции составляют f (x₂) – f (x₁), f (x₃) – f (x₂), .

Приращение функции при переходе от значения x_i к значению x_i+1 будем обозначать: В частности можно взять в качестве значения независимых переменных x и x + 1 . Разность Δf (x) = f (x + 1) — f (x) называется первой разностью или разностью первого порядка. Она может рассматриваться в свою очередь как функция от x, а потому и для нее можно определить разницу:

Введем обозначения ΔΔf (x) = Δ 2 f (x), тогда Δ 2 f (x) = f (x + 2) — 2 f (x + 1) + f (x) и называется разностью второго порядка.

Аналогично можно найти разности третьего, четвертого и т. д. порядков.

Определим разности некоторых важнейших функций.

1) Если f (x) = С, где С — постоянная величина, то
Δf (x) = f (x + 1) – f (x) = С – С = 0.

Понятно, что и все разности следующих порядков будут также равняться нулю.

2) Если f (x) = ax + b, то
Δf = Δf (x + 1) — f (x) = a (x + 1) + b — ax — b = a.

Разница первого порядка линейной функции равна постоянной, а все остальные будут равны нулю.

3) Если f (x) = ax 2 + bx + c, то

Поскольку разница первого порядка является линейной функцией, то разница второго порядка — постоянная, а все последующие разности равны нулю.

4) Если f (x) = a x , то

В экономических исследованиях часто встречаются задачи, в которых время t является независимой переменной, а зависимая переменная определяется для времени t, t + 1, t + 2 и т. д.

Обозначим y_t — значение функции y в момент времени t; y_t+1 — значение функции в момент, сдвинутый на одну единицу, например, на следующий час, на следующую неделю и т. д., y_t+2 — значение функции y в момент, сдвинутый на две единицы и т. д.

Очевидно, что

Откуда:

За разность второго порядка, имеем или
поэтому

Аналогично можно доказать, что

Итак, любую функцию

можно представить в виде: (7.50)
и наоборот.

Определение. Уравнение
(7.51)
называется разностным уравнением n-го порядка.

Решить разностное уравнение n-го порядка — это значит найти такую ​​функцию y_t, которая превращает уравнение (7.50) или (7.51) в тождество.

Решение, в котором есть произвольная постоянная, называется общим; решение, в котором постоянная отсутствует, называется частным.

Определение. Уравнение
(7.52)
где a₀, a₁, . a_n — постоянные числа, называется неоднородным разностным
уравнением n-го порядка с постоянными коэффициентами.

Если в уравнении (7.52) f (t) = 0, то уравнение называется однородным разностным уравнением n-го порядка с постоянными коэффициентами:
(7.53)

Уравнение есть однородное разностное уравнение первого порядка с постоянными коэффициентами a и b, а уравнение — неоднородное разностное уравнение второго порядка с постоянными коэффициентами a, b, c.

ТЕОРЕМА 1. Если решениями однородного разностного уравнения (7.53) является y₁ (t) и y₂ (t), то его решением будет также функция y₁ (t) + y₂ (t).

ТЕОРЕМА 2. Если y (t) является решением однородного разностного уравнения (7.53), то его решением будет также функция Ay (t), где А — произвольная постоянная.

ТЕОРЕМА 3. Если y (t) — частное решение неоднородного уравнения (7.52) и y (t, A₁, A₂, . A_n) — общее решение однородного уравнения (7.53), то общим решением неоднородного разностного уравнения будет функция: y (t) + y (t, A₁, A₂, . A_n).

Эти теоремы схожи с теоремами для дифференциальных уравнений, которые были приведены нами в предыдущем разделе.

Разностные уравнения первого порядка с постоянными коэффициентами

Рассмотрим неоднородное разностное уравнение
(7.54)

Соответствующее ему однородное уравнение будет:
(7.55)

Возьмем функцию и убедимся, что она будет решением уравнения (7.55). Поскольку , тогда . Подставим y_t и y_t-1 в уравнение (7.55):
Итак, является решением уравнения (7.55).

По теореме (2) общее решение однородного разностного уравнения (7.55) является функция , где А — произвольная постоянная.

Пусть — частное решение неоднородного разностного уравнения (7.54). По теореме (3) общим решением неоднородного разностного уравнения (7.54) будет функция

Частное решение найти нетрудно, если f (t) = α, где α — некоторая постоянная. На самом деле, если где u — постоянная. Подставим в уравнение (7.54), имеем: u — au = α, откуда
Итак, общее решение уравнения (7.54) запишем в виде: .

Разностные уравнения второго порядка с постоянными коэффициентами

Пусть задано неоднородное разностное уравнение второго порядка с постоянными коэффициентами:
(7.56)
и соответствующее ему однородное уравнение
(7.57)

Убедимся, что функция будет решением уравнения (7.58). Подставим в уравнение (7.57) (λ ≠ 0), получим Поскольку λ ≠ 0, то поделим на λ t-2 , имеем λ 2 + aλ + b = 0 (7.58)

Это уравнение называется характеристическим уравнением для уравнения (7.57).

Здесь могут иметь место следующие три случая:

1. D = a 2 – 4b > 0, тогда уравнение (7.58) будет иметь два действительных различных корня.
Общее решение уравнения (7.57) запишется в виде:

а общее решение неоднородного уравнения (7.56) запишется так:

2. D = a 2 – 4b = 0, тогда и и

В этом случае однородное уравнение (7.57) примет вид:
(7.59)
Тогда

Легко убедиться, что решением уравнения (7.59) является также функция
Поэтому общим решением уравнения (7.59) является функция а общим решением неоднородного уравнения (7.56) функция

3. D = a 2 – 4b 2 – 5λ + 6 = 0 будет иметь действительные разные корни (D = 25 – 24 = 1 > 0), λ1 =2, λ2 = 3.
Общим решением однородного уравнения является функция

Далее положим, что y_t = y — частное решение неоднородного уравнения, тогда

Таким образом, общим решением неоднородного уравнения является функция Постоянные A₁ и A₂ определим из начальных условий: y₀ = 5, y₁ = 9. Тогда для t = 0 и t = 1 соответственно будем иметь:

Решим эту систему уравнений относительно A₁ и A₂:

Откуда

Итак, — общее решение заданного в условии разностного уравнения.

Примеры применения разностных уравнений в экономических задачах

Пример 1. Пусть некоторая сумма средств выдается под сложный процент p, то к концу t-го года ее размер будет составлять:
Это однородное разностное уравнение первого порядка. Его решением будет функция , где A — некоторая постоянная, которую можно найти из начальных условий.

Если положить y₀ = F , то A = F, откуда

Это известная формула величины фонда F, который выдается под сложный процент.

Пример 2. Пусть величина предложения сельскохозяйственной продукции в t-м году есть функция цены прошлого года а спрос на эту продукцию есть функция цены в этом году. Следовательно, спрос: а предложение

Цена равновесия для данной продукции определяется равенством:
а это разностное уравнение первого порядка.

Положим, что функция спроса определяется формулой а функция предложения — формулой

Цена равновесия запишется: то есть Решением этого уравнения является функция Постоянная A определяется из начальных условий, для t = 0 цена составляет p₀.

Тогда p₀ = A и решением уравнения является функция
Если начальная цена p₀ = 0, то p_t = 0 для всех значений t.

Следовательно, цена не подлежит изменению.

Вообще говоря, функция предложения — возрастающая, а потому b > 0; а функция спроса — убывающая, и поэтому a

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Дифференциальные уравнения первого порядка

Далее в тексте – функции своих аргументов. Штрих ′ означает производную по аргументу. – постоянные.

Дифференциальные уравнения первого порядка, разрешенные относительно производной

Как решать дифференциальные уравнения первого порядка

Пусть мы имеем дифференциальное уравнение первого порядка, разрешенное относительно производной:
.
Разделив это уравнение на , при , мы получим уравнение вида:
,
где .

Далее смотрим, не относятся ли эти уравнения к одному из перечисленных ниже типов. Если нет, то перепишем уравнение в форме дифференциалов. Для этого пишем и умножаем уравнение на . Получаем уравнение в форме дифференциалов:
.

Если это уравнение не является уравнением в полных дифференциалах, то считаем, что в этом уравнении – независимая переменная, а – это функция от . Разделим уравнение на :
.
Далее смотрим, не относится ли это уравнение к одному из, перечисленных ниже типов учитывая, что и поменялись местами.

Если и для этого уравнения не найден тип, то смотрим, нельзя ли упростить уравнение простой подстановкой. Например, если уравнение имеет вид:
,
то замечаем, что . Тогда делаем подстановку . После этого уравнение примет более простой вид:
.

Если и это не помогает, то пытаемся найти интегрирующий множитель ⇓.

Уравнения с разделяющимися переменными

Уравнения, приводящиеся к уравнениям с разделяющимися переменными

Делаем подстановку . Тогда
;
.
Далее разделяем переменные и интегрируем.
Подробнее >>>

Однородные уравнения

Решаем подстановкой:
,
где – функция от . Тогда
;
.
Разделяем переменные и интегрируем.
Подробнее >>>

Уравнения, приводящиеся к однородным

Вводим переменные и :
;
.
Постоянные и выбираем так, чтобы свободные члены обратились в нуль:
;
.
В результате получаем однородное уравнение в переменных и .
Подробнее >>>

Обобщенные однородные уравнения

Делаем подстановку . Получаем однородное уравнение в переменных и .
Подробнее >>>

Линейные дифференциальные уравнения

Есть три метода решения линейных уравнений.

1) Метод интегрирующего множителя.
Умножаем уравнение на интегрирующий множитель :
;
.
Далее интегрируем.
Подробнее >>>

2) Метод Бернулли.
Ищем решение в виде произведения двух функций и от переменной :
.
;
.
Одну из этих функций мы можем выбрать произвольным образом. Поэтому в качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .
Подробнее >>>

3) Метод вариации постоянной (Лагранжа).
Здесь мы сначала решаем однородное уравнение:

Общее решение однородного уравнения имеет вид:
,
где – постоянная. Далее мы заменяем постоянную на функцию , зависящую от переменной :
.
Подставляем в исходное уравнение. В результате получаем уравнение, из которого определяем .
Подробнее >>>

Уравнения Бернулли

Подстановкой уравнение Бернулли приводится к линейному уравнению.

Также это уравнение можно решать методом Бернулли. То есть ищем решение в виде произведения двух функций, зависящих от переменной :
.
Подставляем в исходное уравнение:
;
.
В качестве выбираем любое не нулевое решение уравнения:
.
Определив , получаем уравнение с разделяющимися переменными для .

Уравнения Риккати

Оно не решается в общем виде. Подстановкой

уравнение Риккати приводится к виду:
,
где – постоянная; ; .
Далее, подстановкой:

оно приводится к виду:
,
где .

Свойства уравнения Риккати и некоторые частные случаи его решения представлены на странице
Дифференциальное уравнение Риккати >>>

Уравнения Якоби

Уравнения в полных дифференциалах

При условии
.
При выполнении этого условия, выражение в левой части равенства является дифференциалом некоторой функции:
.
Тогда
.
Отсюда получаем интеграл дифференциального уравнения:
.

Для нахождения функции , наиболее удобным способом является метод последовательного выделения дифференциала. Для этого используют формулы:
;
;
;
.
Подробнее >>>

Интегрирующий множитель

Если дифференциальное уравнение первого порядка не приводится ни к одному из перечисленных типов, то можно попытаться найти интегрирующий множитель . Интегрирующий множитель – это такая функция , при умножении на которую, дифференциальное уравнение становится уравнением в полных дифференциалах. Дифференциальное уравнение первого порядка имеет бесконечное число интегрирующих множителей. Однако, общих методов для нахождения интегрирующего множителя нет.
Подробнее >>>

Уравнения, не решенные относительно производной y’

Уравнения, допускающие решение относительно производной y’

Сначала нужно попытаться разрешить уравнение относительно производной . Если это возможно, то уравнение может быть приведено к одному из перечисленных выше типов.

Уравнения, допускающие разложение на множители

Если удастся уравнение разложить на множители:
,
то задача сводится к последовательному решению более простых уравнений:
;
;

;
Подробнее >>>

Уравнения, не содержащие x и y

Уравнения, не содержащие x или y

или
Ищем решение в параметрическом виде. Вводим параметр . Полагаем . Тогда
или .
Далее интегрируем уравнение:
;
.
В результате получаем выражение второй переменной через параметр .

Более общие уравнения:
или
также решаются в параметрическом виде. Для этого нужно подобрать такую функцию , чтобы из исходного уравнения можно было выразить или через параметр .
Чтобы выразить вторую переменную через параметр , интегрируем уравнение:
;
.
Подробнее >>>

Уравнения, разрешенные относительно y

Уравнения Клеро

Такое уравнение имеет общее решение

Подробнее >>>

Уравнения Лагранжа

Решение ищем в параметрическом виде. Полагаем , где – параметр.
Подробнее >>>

Уравнения, приводящиеся к уравнению Бернулли

Эти уравнения приводятся к уравнению Бернулли, если искать их решения в параметрическом виде, введя параметр и делая подстановку .
Подробнее >>>

Использованная литература:
В.В. Степанов, Курс дифференциальных уравнений, «ЛКИ», 2015.
Н.М. Гюнтер, Р.О. Кузьмин, Сборник задач по высшей математике, «Лань», 2003.

Автор: Олег Одинцов . Опубликовано: 20-05-2016