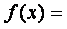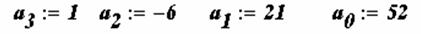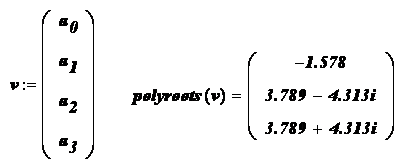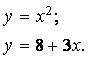Графический метод решения систем нелинейных уравнений, 8-й класс
Разделы: Математика
Класс: 8
Цель урока:
- совершенствование навыки построения графиков функций;
- применение умений, полученных на уроках информатики (графики в Ехсе1);
- развитие современной функциональной грамотности.
Задачи урока:
- Обучающие: знакомство с графическим способом решения систем нелинейных уравнений; развитие умения применять теоретические знания в процессе
решения систем уравнений; - Развивающие: развитие познавательного интереса к предмету; развитие навыка самостоятельного поиска необходимой
информации; развитие навыка самоконтроля. - Воспитательные: развитие культуры общения; желания помочь товарищу в затруднительных ситуациях.
- Здоровье-сберегающие: соблюдение гигиены умственного труда при работе с компьютером.
Виды используемых на уроке средств ИКТ: СD, универсальные, ресурсы Интернет.
Необходимое аппаратное и программное обеспечение: Мультимедийный компьютер, программные средства, наушники/
Оборудование: Чертежные инструменты.
Ход урока
I. Организационный момент
Приветствие и размещение на рабочих местах.
Учитель. Мы продолжаем изучение большой темы “Решение систем нелинейных уравнений”. Какие способы решения нами были рассмотрены? (Метод постановки, метод сложения, метод введения новых неизвестных, метод решения однородных уравнений.)
Какой еще способ нам известен из курса алгебры седьмого класса? (Графический.)
Почему он так называется? (В одной и той же системе координат строим графики обоих уравнений и находим координаты точек их пересечения.)
! Цель сегодняшнего урока: научиться решать нелинейные системы уравнений графическим методом, Используя чертежные инструменты и программу построения графиков на компьютере.
Систему координат, в которой мы будем строить графики, называют декартовой,. Почему? Ответ на этот вопрос вы узнаете, посмотрев диск.
Учащиеся переходят к компьютерам, надевают наушники и читают и слушают информацию из диска “Алгебра Кирилла и Мефодия 7–8”, тема “Графики функций” о Рене Декарте и созданной им системе координат.
П. Актуализация опорных знаний
Фронтальная беседа. Презентация “Графики функций”.
1. Какие функции нам известны? Как называются их графики?
а) у = кх + Ь – линейная функция. Графиком является прямая, которую строим по двум точкам.
Если к > 0, то угол наклона прямой к положительному направлению от Ох острый.
Если к 2 квадратная функция. Графиком является парабола. Для построения графика используем таблицу значений.
в) обратная пропорциональность: y = k/x, графиком является гипербола В(f)=x
г) y = 

д) уравнение окружности
х 2 + у 2 = R 2
(х – а) 2 + (у – b) 2 = R 2
0(а; b)
III. Объяснение нового материала
В чем состоит графический метод решения систем уравнений? (В одной и той же системе координат строим графики уравнений.)
Координаты точки пересечения и будут являться решением данной системы.
IV. Закрепление темы
1) Решить систему уравнений:
в) 

V. Работа на компьютере
№ 130 из учебника Виленкин:
а) 

г) 

а) 

Д/з на стр. 205 № 162 (а,б)
VI. Итог урока
Применение современной техники позволяет сделать процесс решения систем уравнений графическим методом значительно быстрее, но необходимо уметь строить графики функций.
Учебник: Н.Я. Виленкин Н.Я. Алгебра. 8. – М.: Просвещение, 2001.
Системы уравнений с двумя переменными
п.1. Понятие системы уравнений с двумя переменными и её решения
п.2. Графический метод решения системы уравнений с двумя переменными
Поскольку каждое из уравнений с двумя переменными можно изобразить в виде графика на плоскости, графический метод решения систем таких уравнений достаточно удобен.
п.3. Примеры
Пример 1. Решите графическим способом систему уравнений:
а) \( \left\< \begin
\( \mathrm
\( \mathrm <4x+3y=0>\) – прямая \( \mathrm
Система имеет два решения (–3; 4) и (3; –4)
Ответ: <(–3; 4) ; (3; –4)>.
б) \( \left\< \begin
\( \mathrm
y – x = 4 – прямая y = x + 4
Система имеет два решения (–5; –1) и (1; 5)
Ответ: <(–5; –1) ; (1; 5)>.
в) \( \left\< \begin
x 2 + y = 1 – парабола y = –x 2 + 1
x 2 – y = 7 – парабола y = x 2 – 7
Система имеет два решения (–2; –3) и (2; –3)
Ответ: <(–2; –3) ; (2; –3)>.
г) \( \left\< \begin
xy = 1 – гипербола \( \mathrm
x 2 + y 2 = 2 – окружность с центром в начале координат, радиусом \( \mathrm<\sqrt<2>> \)
Система имеет два решения (–1; –1) и (1; 1)
Ответ: <(–1; –1) ; (1; 1)>.
Пример 2*. Решите графическим способом систему уравнений
a) \( \left\< \begin
x 3 – y = 1 – кубическая парабола y = x 3 – 1, смещённая на 1 вниз.
\( \mathrm <\frac1x-y=1>\) – гипербола \( \mathrm
Система имеет два решения (–1; –2) и (1; 0)
Ответ: <(–1; –2) ; (1; 0)>.
б) \( \left\< \begin
|x| + |y| = 2 – квадрат с диагоналями 4, лежащими на осях
x 2 + y 2 = 4 – окружность с центром в начале координат, радиусом 2
Система имеет четыре решения (2; 0), (0; 2) , (–2; 0) и (0; –2)
Ответ: <(2; 0) ; (0; 2) ; (–2; 0) ; (0; –2)>.
в) \( \left\< \begin
y – x 2 = 4x + 6 – парабола y = (x 2 + 4x + 4) + 2 = (x + 2) 2 + 2, ветками вверх, смещённая на 2 влево и на 2 вверх
y + |x| = 6 – ломаная, y = –|x| + 6. Для x > 0, y = –x + 6, для x 0, y = x, для x
Решение нелинейных уравнений и систем уравнений в пакете MathCAD
Решение нелинейных уравнений
Вычисление корней численными методами включает два основных этапа:
· уточнение корней до заданной точности.
Рассмотрим эти два этапа подробно.
Отделение корней нелинейного уравнения
Учитывая легкость построения графиков функций в MathCAD , в дальнейшем будет использоваться графический метод отделения корней.
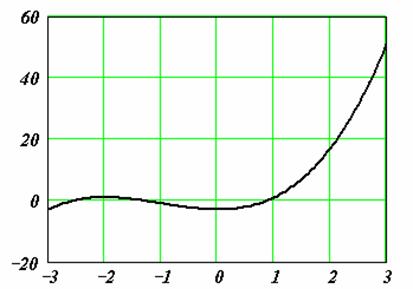
Пример. Дано алгебраическое уравнение
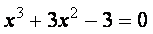
Определить интервалы локализации корней этого уравнения.
Пример. Дано алгебраическое уравнение
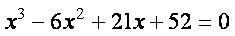
Определить интервалы локализации корней этого уравнения.
На рисунке приведен график функции 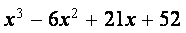
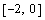
Уточнение корней нелинейного уравнения
Для уточнения корня используются специальные вычислительные методы такие, как метод деления отрезка пополам, метод хорд, метод касательных (метод Ньютона) и многие другие.
Функция root . В MathCAD для уточнения корней любого нелинейного уравнения (не обязательно только алгебраического) введена функция root , которая может иметь два или четыре аргумента, т.е. 

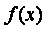
Пример. Используя функцию 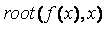
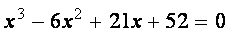
Заметим, что для вычисления всех трех корней использовался прием понижения порядка алгебраического уравнения, рассмотренный в п. 8.1.1. ¨
Функция root с двумя аргументами требует задания (до обращения к функции) переменной 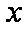
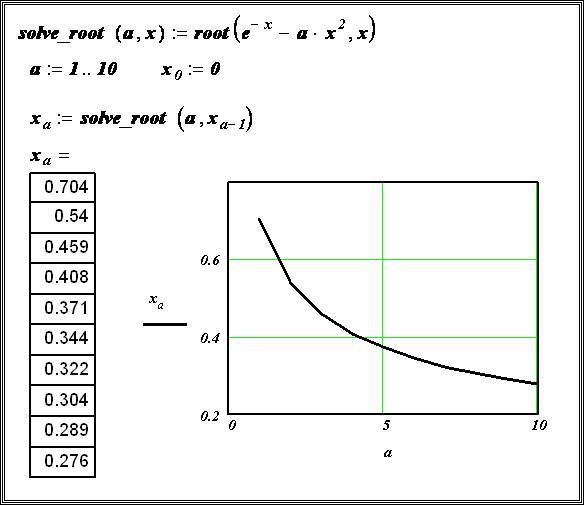
Пример 8.1.5. Используя функцию root , вычислить изменения корня нелинейного уравнения 
Функция polyroots . Для вычисления всех корней алгебраического уравнения порядка 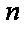
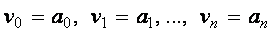
Пример. Используя функцию polyroots , найти все три корня уравнения 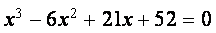
Блок Given . При уточнении корня нелинейного уравнения можно использовать специальный вычислительный блок Given , имеющий следующую структуру:
Решаемое уравнение задается в виде равенства, в котором используется «жирный» знак равно, вводимый с палитры Логический .
Ограничения содержат равенства или неравенства, которым должен удовлетворять искомый корень.
Функция Find уточняет корень уравнения, вызов этой функции имеет вид Find ( x ), где x – переменная, по которой уточняется корень. Если корня уравнения на заданном интервале не существует, то следует вызвать функцию Minerr ( x ), которая возвращает приближенное значение корня.
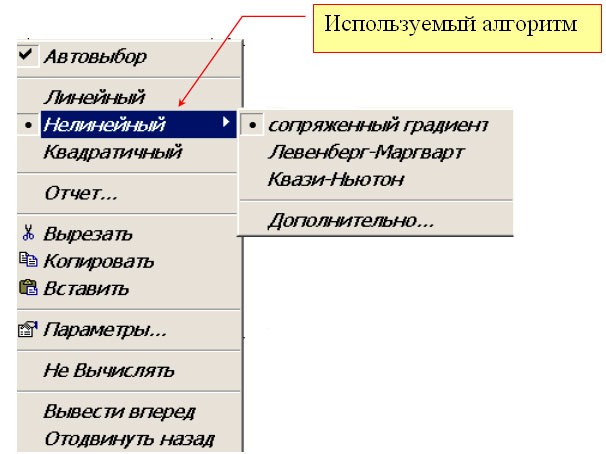
Для выбора алгоритма уточнения корня необходимо щелкнуть правой кнопкой мыши на имени функции Find ( x ) и в появившемся контекстном меню (см. рисунок) выбрать подходящий алгоритм.
Аналогично можно задать алгоритм решения и для функции Minerr ( x ).
Использование численных методов в функциях Find ( x ), Minerr ( x ) требует перед блоком Given задать начальные значения переменным, по которым осуществляется поиск корней уравнения.
Пример. Используя блок Given , вычислите корень уравнения 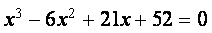
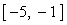
Решение систем уравнений
В зависимости от того, какие функции входят в систему уравнений, можно выделить два класса систем:
· алгебраические системы уравнений;
· трансцендентные системы уравнений.
Среди алгебраических систем уравнений особое место занимают системы линейных алгебраических уравнений (СЛАУ).
Системы линейных алгебраических уравнений
Системой линейных алгебраических уравнений (СЛАУ) называется система вида:
В матричном виде систему можно записать как
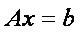
где 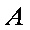
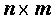
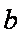

Для вычисления решения СЛАУ следует использовать функцию lsolve , обращение к которой имеет вид: lsolve (А, b ), где А – матрица системы, 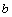
Решение систем нелинейных уравнений
MathCAD дает возможность находить решение системы уравнений численными методами, при этом максимальное число уравнений в MathCAD 2001 i доведено до 200.
Для решения системы уравнений необходимо выполнить следующие этапы.
Задание начального приближения для всех неизвестных, входящих в систему уравнений. При небольшом числе неизвестных этот этап можно выполнить графически, как показано в примере.
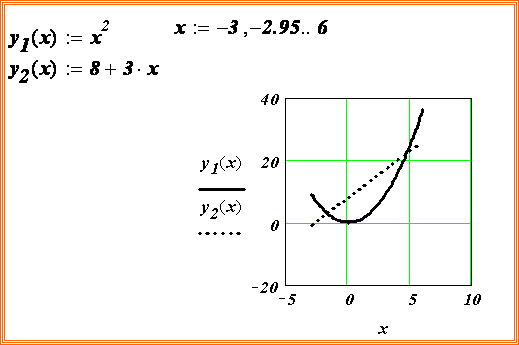
Пример. Дана система уравнений:
Определить начальные приближения для решений этой системы.
Видно, что система имеет два решения: для первого решения в качестве начального приближения может быть принята точка (-2, 2), а для второго решения – точка (5, 20). ¨
Вычисление решения системы уравнений с заданной точностью . Для этого используется уже известный вычислительный блок Given .
Функция Find вычисляет решение системы уравнений с заданной точностью, и вызов этой функции имеет вид Find ( x ), где x – список переменных, по которым ищется решение. Начальные значения этим переменным задаются в блоке . Число аргументов функции должно быть равно числу неизвестных.
Следующие выражения недопустимы внутри блока решения:
· ограничения со знаком ¹ ;
· дискретная переменная или выражения, содержащие дискретную переменную в любой форме;
· блоки решения уравнений не могут быть вложены друг в друга, каждый блок может иметь только одно ключевое слово Given и имя функции Find (или Minerr ).
Пример. Используя блок Given , вычислить все решения системы предыдущего примера. Выполнить проверку найденных решений.
Пример. Используя функцию 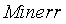
http://reshator.com/sprav/algebra/9-klass/sistemy-uravnenij-s-dvumya-peremennymi/
http://pers.narod.ru/study/mathcad/07.html