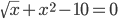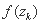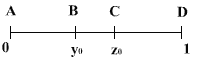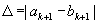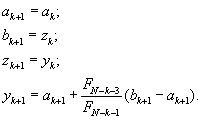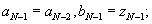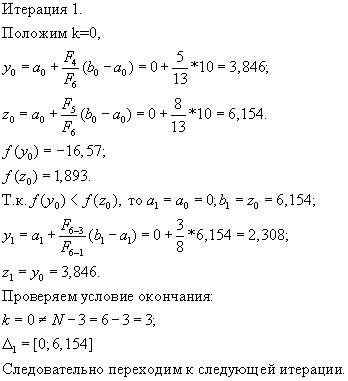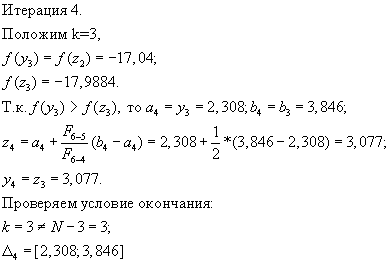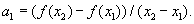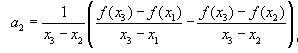Метод половинного деления (метод дихотомии или метод бисекции)
Теорема 2. Итерационный процесс половинного деления сходится к искомому корню ξ с любой наперед заданной точностью ε.
Доказательство: Рассмотрим последовательность чисел ξi являющихся приближением корня на i -ом шаге.
ξi=½(bi+ai), i=0,1.
где a0=a; b0=b; ai;bi — границы подынтервалов, в которых f(ai)f(bi) 0 мы ни задали, всегда можно найти такое n , что 
Графически метод дихотомии выглядит следующим образом
|f(c)|≤δ f(a)f(c) 10 = 1024 ≈ 10 3 раз. За 20 итераций (n=2) уменьшается в 2 20 ≈ 10 6 раз.
Пример №1 . Найти экстремум функции: y=5x 2 -4x+1 методом дихотомии, если ε=0.1, а исходный интервал [0,10].
- Решение
- Видео решение
Пример №3 . Методом бисекции найти решение нелинейного уравнения на отрезке [a,b] с точностью ε = 10 -2 . Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε = 10 -4 . Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности число итераций.
sqrt(t)+x 2 = 10, a = 2.6, b = 3
Найдем корни уравнения:
Используем для этого Метод половинного деления (метод дихотомии)..
Считаем, что отделение корней произведено и на интервале [a,b] расположен один корень, который необходимо уточнить с погрешностью ε.
Итак, имеем f(a)f(b) 1 /2(a+b) и вычисляем f(c). Проверяем следующие условия:
1. Если |f(c)| 1 /2 n (b-a)
В качестве корня ξ. возьмем 1 /2(an+bn). Тогда погрешность определения корня будет равна (bn – an)/2. Если выполняется условие:
(bn – an)/2 1 /2(an+bn).
Решение.
Поскольку F(2.6)*F(3) 0, то a=2.8
Итерация 2.
Находим середину отрезка: c = (2.8 + 3)/2 = 2.9
F(x) = 0.113
F(c) = -0.487
Поскольку F(c)•F(x) 0, то a=2.825
Остальные расчеты сведем в таблицу.
| N | c | a | b | f(c) | f(x) |
| 1 | 2.6 | 3 | 2.8 | -1.6275 | -0.4867 |
| 2 | 2.8 | 3 | 2.9 | -0.4867 | 0.1129 |
| 3 | 2.8 | 2.9 | 2.85 | 0.1129 | -0.1893 |
| 4 | 2.8 | 2.85 | 2.825 | -0.1893 | -0.3386 |
| 5 | 2.825 | 2.85 | 2.8375 | -0.3386 | -0.2641 |
| 6 | 2.8375 | 2.85 | 2.8438 | -0.2641 | -0.2267 |
Ответ: x = 2.8438; F(x) = -0.2267
Решение было получено и оформлено с помощью сервиса Метод Ньютона онлайн
Пример №2 . Локализовать корень нелинейного уравнения f(x) = 0 и найти его методом бисекции с точностью ε1 = 0,01. Выбрав полученное решение в качестве начального приближения, найти решение уравнения методом простой итерации с точностью ε2 = 0,0001. Для метода простой итерации обосновать сходимость и оценить достаточное для достижения заданной точности ε2 число итераций.
Метод дихотомии решения нелинейных уравнений
На практике очень часто приходится решать задачи, связанные с решением нелинейных уравнений. Дихотомия или метод деления пополам — наиболее простой и надежный метод вычисления корней уравнения f (х) = 0, основанный на пошаговом сужении промежутка, в котором находится единственный корень уравнения, пока не добиться заданной точности.
Возьмем две точки х0 и х1, в которых значения функции f (х0) и f (х1) имеют разные знаки. В этом случае между ними имеется хоть один корень функции f.
Разделим промежуток между точками х0 и х1 пополам, обозначим середину отрезка точкой х2, которая равняется: х2 = (х0 + х1) / 2. Тогда f (х2) f (х0)
Метод дихотомии решения нелинейных уравнений f (x)=0
| a = | b = |
Введите левую часть уравнения (неизвестная — x):
Метод половинного деления (дихотомии)
Постановка задачи.
Тебуется наути безусловный минимум функции f(x) одной переменной, т.е. такую точку 
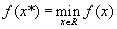
Стратегия поиска.
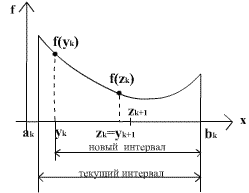
Метод относится к последовательным стратегиям и позволяет исключить из дальнейшего рассмотрения на каждой итерации ровно половину текущего интервала неопределенности. Задается начальный интервал неопределенности и требуемая точность.
Алгоритм основан на анализе значений функции в трех точках, равномерно распределенных на текущем интервале (делящих его на четыре равные части). Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1.Задать начальный интервал неопределенности 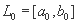

Шаг 2.Положить k=0.
Шаг 3.Вычислить среднюю точку 
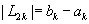

Шаг 4.Вычислить точки: 

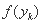
Шаг 5.Сравнить значения 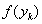
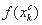
а) если
Определение. Точка производит «золотое сечение» отрезка, если отношение длины всего отрезка к большей части равно отношению большей части к меньшей.
Рассмотрим для простоты отрезок [0,1] единичной длины.
Ясно, что на отрезке имеется две таких точки 
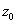

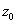
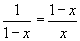

Стратегия поиска.
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и требуемая точность. Алгоритм основан на анализе величин функции в двух точках. В качестве точек вычисления функции выбираются точки золотого сечения. Тогда учетом свойств золотого сечения на каждой итерации, кроме первой, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1.Задать начальный интервал неопределенности 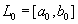

Шаг 2.Положить k=0.
Шаг 3.Вычислить точки 
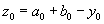
Шаг 4.вычислить значения : 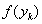
Шаг 5.Сравнить значения 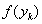
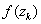
а) если 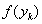
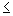
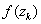
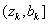
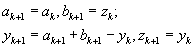
Перейти к шагу 6.
б) если 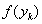
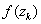
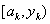
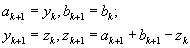
Перейти к шагу 6.
Шаг 6.Вычислить
а) если 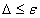
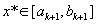

б) если 
Сходимость.
Для метода золотого сечения характеристика относительного уменьшения начального интервала неопределенности находится по формуле 
Пример.
Задание.
Определить методом Золотого сечения минимум функции 


Метод Фибоначчи.
Постановка задачи.
Тебуется найти безусловный минимум функции f(x) одной переменной, т.е. такую точку 
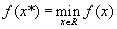
В методе Фибоначчи реализована стратегия, обеспечивающая максимальное гарантированное сокращение интервала неопределенности при заданном количестве вычислений функции. Эта стратегия опирается на числа Фибоначчи.
Определение. Числа Фибоначчи определяются следующим образом:
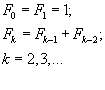
Последовательность чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,… .
Стратегия поиска.
Метод относится к последовательным стратегиям. Задается начальный интервал неопределенности и количество N вычислений функции. Алгоритм основан на анализе величин функции в двух точках. Точки вычисления функции находятся с использованием последовательности из N+1 чисел Фибоначчи. Как и в методе золотого сечения, на первой итерации требуется два вычисления функции, а на каждой последующей итерации, требуется только одно новое вычисление функции. Поиск заканчивается, когда длина текущего интервала неопределенности оказывается меньше установленной величины.
Алгоритм.
Шаг 1.Задать начальный интервал неопределенности 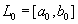

Шаг 2.Найти количество N вячислений функции как наименьшее целое число, при котором удовлетворяется условие 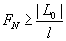

Шаг 3.Положить k=0.
Шаг 4.Вычислить значения :
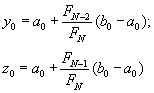
Шаг 5.Вычислить 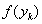
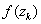
Шаг 6.Сравнить 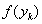
а) если 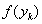
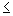
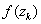
Перейти к шагу 7;
б) если 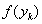
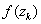
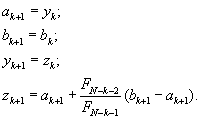
Шаг 7.Проверить условие окончания и в случае необходимости сделать заключительное N-е вычисление функции для получения решения:
а) если 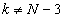
б) если k=N-3, то всегда 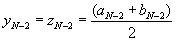

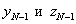
o Если 
o Если 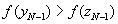
Поиск завершен и 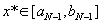
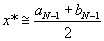
Сходимость.
Для метода Фибоначчи характеристика относительного уменьшения начального интервала неопределенности находится по формуле 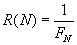
Пример.
Определить методом Фибоначчи минимум функции 

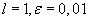
Метод Пауэлла.
Основная идея методов полиномиальной аппроксимации связана с возможностью аппроксимации гладкой функции полиномом и последующего использования аппроксимирующего полинома для оценивания координаты точки оптимума. Необходимыми условиями эффективной реализации такого подхода являются унимодальность и непрерывность исследуемой функции.
Согласно теореме Вейерштрасса об аппроксимации, непрерывную функцию в некотором интервале можно аппроксимировать полиномом достаточно высокого порядка. Следовательно, если функция унимодальна и найден полином, который достаточно точно ее аппроксимирует, то координаты точки оптимума функции можно оценить путем вычисления координаты точки оптимума полинома.
Простейшим вариантом полиномиальной аппроксимации является квадратичная аппроксимация, которая основана на том факте, что функция, принимающая минимальное значение во внутренней точке интервала, должна быть, по крайней мере, квадратичной. Если же функция линейная, то ее оптимальное значение может достигаться только в одной из двух граничных точек интервала. Таким образом, при реализации метода оценивания с использованием квадратичной аппроксимации предполагается, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, а затем использовать построенный полином для оценивания координаты точки истинного минимума функции.
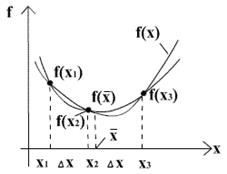
Пусть известны значения функции f(x) в трех разных точках 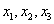

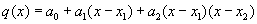
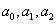
Аналогично получаем 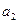
Квадратичная функция q(x) достигает минимума в точке 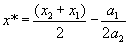
Поскольку функция f(x) на рассматриваемом интервале обладает свойством унимодальности, а аппроксимирующий квадратичный полином также является унимодальной функцией, то можно ожидать, что величина 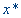
Стратегия поиска.
Метод Пауэлла относится к последовательным стратегиям. Задается начальная точка и с помощью пробного шага находится три точки так, чтобы они были как можно ближе к искомой точке минимума. В полученных точках вычисляются значения функции. Затем строится интерполяционный полином второй степени, проходящий через эти точки. В качестве приближения точки минимума берется точка минимума полинома. Поиск заканчивается, когда полученная точка отличается от лучшей из трех опорных точек не более чем на заданную величину.
Алгоритм.
Шаг 1.Задать начальную точку 
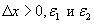
Шаг 2.
Шаг 3.Вычислить 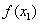
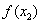
Шаг 4.Сравнить 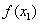
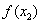
o Если 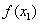
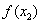

o Если
http://infofaq.ru/metod-dihotomii-resheniya-nelinejnyh-uravnenij.html
http://poisk-ru.ru/s81020t1.html