Как решить уравнение с интегралом калькулятор

Калькулятор Интегралов. Решение Определенных и Неопределенных Интегралов (первообразных)

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Вычислить неопределенный интеграл (первообразную).

Этот математический калькулятор онлайн поможет вам вычислить неопределенный интеграл (первообразную). Программа для вычисления неопределенного интеграла (первообразной) не просто даёт ответ задачи, она приводит подробное решение с пояснениями, т.е. отображает процесс интегрирования функции.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> С 9 января 2019 года вводится новый порядок получения подробного решения некоторых задач. Ознакомтесь с новыми правилами >> —> Введите подинтегральную функцию Вычислить

Немного теории.

Первообразная (неопределенный интеграл)

Ранее мы по заданной функции, руководствуясь различными формулами и правилами, находили ее производную. Производная имеет многочисленные применения: это скорость движения (или, обобщая, скорость протекания любого процесса); угловой коэффициент касательной к графику функции; с помощью производной можно исследовать функцию на монотонность и экстремумы; она помогает решать задачи на оптимизацию.

Но наряду с задачей о нахождении скорости по известному закону движения встречается и обратная задача — задача о восстановлении закона движения по известной скорости. Рассмотрим одну из таких задач.

Пример 1. По прямой движется материальная точка, скорость ее движения в момент времени t задается формулой v=gt. Найти закон движения.
Решение. Пусть s = s(t) — искомый закон движения. Известно, что s'(t) = v(t). Значит, для решения задачи нужно подобрать функцию s = s(t), производная которой равна gt. Нетрудно догадаться, что \( s(t) = \frac <2>\). В самом деле
\( s'(t) = \left( \frac <2>\right)’ = \frac<2>(t^2)’ = \frac <2>\cdot 2t = gt \)
Ответ: \( s(t) = \frac <2>\)

Сразу заметим, что пример решен верно, но неполно. Мы получили \( s(t) = \frac <2>\). На самом деле задача имеет бесконечно много решений: любая функция вида \( s(t) = \frac <2>+ C \), где C — произвольная константа, может служить законом движения, поскольку \( \left( \frac <2>+C \right)’ = gt \)

Чтобы задача стала более определенной, нам надо было зафиксировать исходную ситуацию: указать координату движущейся точки в какой-либо момент времени, например при t = 0. Если, скажем, s(0) = s₀, то из равенства s(t) = (gt 2 )/2 + C получаем: s(0) = 0 + С, т. е. C = s₀. Теперь закон движения определен однозначно: s(t) = (gt 2 )/2 + s₀.

В математике взаимно обратным операциям присваивают разные названия, придумывают специальные обозначения, например: возведение в квадрат (х 2 ) и извлечение квадратного корня ( \( \sqrt \) ), синус (sin x) и арксинус (arcsin x) и т. д. Процесс нахождения производной по заданной функции называют дифференцированием, а обратную операцию, т. е. процесс нахождения функции по заданной производной, — интегрированием.

Сам термин «производная» можно обосновать «по-житейски»: функция у = f(x) «производит на свет» новую функцию у’ = f'(x). Функция у = f(x) выступает как бы в качестве «родителя», но математики, естественно, не называют ее «родителем» или «производителем», они говорят, что это, по отношению к функции у’ = f'(x), первичный образ, или первообразная.

Определение. Функцию y = F(x) называют первообразной для функции y = f(x) на промежутке X, если для \( x \in X \) выполняется равенство F'(x) = f(x)

На практике промежуток X обычно не указывают, но подразумевают (в качестве естественной области определения функции).

Приведем примеры.
1) Функция у = х 2 является первообразной для функции у = 2х, поскольку для любого х справедливо равенство (x 2 )’ = 2х
2) Функция у = х 3 является первообразной для функции у = 3х 2 , поскольку для любого х справедливо равенство (x 3 )’ = 3х 2
3) Функция у = sin(x) является первообразной для функции y = cos(x), поскольку для любого x справедливо равенство (sin(x))’ = cos(x)

При нахождении первообразных, как и производных, используются не только формулы, но и некоторые правила. Они непосредственно связаны с соответствующими правилами вычисления производных.

Мы знаем, что производная суммы равна сумме производных. Это правило порождает соответствующее правило нахождения первообразных.

Правило 1. Первообразная суммы равна сумме первообразных.

Мы знаем, что постоянный множитель можно вынести за знак производной. Это правило порождает соответствующее правило нахождения первообразных.

Правило 2. Если F(x) — первообразная для f(x), то kF(x) — первообразная для kf(x).

Теорема 1. Если y = F(x) — первообразная для функции y = f(x), то первообразной для функции у = f(kx + m) служит функция \( y=\frac<1>F(kx+m) \)

Теорема 2. Если y = F(x) — первообразная для функции y = f(x) на промежутке X, то у функции у = f(x) бесконечно много первообразных, и все они имеют вид y = F(x) + C.

Методы интегрирования

Метод замены переменной (метод подстановки)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.
Пусть требуется вычислить интеграл \( \textstyle \int F(x)dx \). Сделаем подстановку \( x= \varphi(t) \) где \( \varphi(t) \) — функция, имеющая непрерывную производную.
Тогда \( dx = \varphi ‘ (t) \cdot dt \) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой:
\( \int F(x) dx = \int F(\varphi(t)) \cdot \varphi ‘ (t) dt \)

Интегрирование выражений вида \( \textstyle \int \sin^n x \cos^m x dx \)

Если m нечётное, m > 0, то удобнее сделать подстановку sin x = t.
Если n нечётное, n > 0, то удобнее сделать подстановку cos x = t.
Если n и m чётные, то удобнее сделать подстановку tg x = t.

Интегрирование по частям

Интегрирование по частям — применение следующей формулы для интегрирования:
\( \textstyle \int u \cdot dv = u \cdot v — \int v \cdot du \)
или:
\( \textstyle \int u \cdot v’ \cdot dx = u \cdot v — \int v \cdot u’ \cdot dx \)

источники:

http://www.integral-calculator.ru/

http://www.math-solution.ru/math-task/indefinite-integral

Верхний предел

∫

Нижний предел

Ввод распознает различные синонимы функций, как asin , arsin , arcsin

Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)

Список математических функций и констант :

• ln(x) — натуральный логарифм

• sh(x) — гиперболический синус

• ch(x) — гиперболический косинус

• th(x) — гиперболический тангенс

• cth(x) — гиперболический котангенс

• sch(x) — гиперболический секанс

• csch(x) — гиперболический косеканс

• arsh(x) — обратный гиперболический синус

• arch(x) — обратный гиперболический косинус

• arth(x) — обратный гиперболический тангенс

• arcth(x) — обратный гиперболический котангенс

• arsch(x) — обратный гиперболический секанс

• arcsch(x) — обратный гиперболический косеканс

Калькулятор Интегралов

Вычисление интегралов онлайн
— по шагам и с графиками!

Калькулятор Интегралов позволяет вычислять интегралы и первообразные функций онлайн — совершенно бесплатно!

Наш Калькулятор позволяет проверить решение Ваших математических заданий. Он поможет вам с решением задачи показывая весь ход решения шаг за шагом. Поддерживаются все виды интегрирования включая специальные функции.

Калькулятор Интегралов поддерживает вычисление определённых и неопределённых (первообразных функций) интегралов включая интегрирование функций с несколькими переменными. Кроме этого Вы можете проверить результат своего решения! Интерактивные графики помогут представить и лучше понять функции интегралов.

Чтобы узнать больше о том как пользоваться Калькулятором Интегралов, загляните в раздел «Справка» или ознакомьтесь с примерами.

Ну что ж, теперь — вперед! Успешного интегрирования!

Введите функцию, которую вы хотите проинтегрировать в Калькулятор Интегралов. Не вводите «f(x) =» часть и дифференциал «dx«! Калькулятор Интегралов сразу показывает математическое выражение в графическом виде, прямо в процессе ввода. Убедитесь, что это выражение соответствует тому, что Вы хотели ввести. Используйте скобки если понадобится, например «a/(b+c)«.

В разделе «Примеры», приведены некоторые из функций которые Калькулятор Интегралов способен вычислять.

После того как Вы закончили вводить вашу функцию, нажмите «=» и Калькулятор Интегралов выдаст результат.

В разделе «Настройки» переменная интегрирования и пределы интегрирования могут быть установлены/изменены. Если пределы интегрирования не будут указаны, то будет вычислена только лишь первообразная функция.

Щелчок мышки на примере вводит его в Калькулятор Интегралов. Простое наведение мышки — показывает текст выражения.

Настройте параметры калькулятора:

Переменная интегрирования:
Верхний предел (до):	+∞
Нижний предел (от):	–∞
Использовать только численное интегрирование?
Упрощать выражения интенсивнее?
Упрощать все корни? (√ x² станет x, а не \|x\|)
Использовать комплексные числа (ℂ)?
Использовать числа с запятой вместо дробей?

Генератор заданий для тренировки позволяет сгенерировать сколько угодно различных случайных заданий.

Ниже Вы найдете настройки конфигурации и один из предложенных вариантов задания. Вы можете взяться за его решение (тогда оно будет введено в Калькулятор) или сгенерировать новое.

Вычисляем интеграл: Введите Ваш результат:

Следующее выражение будет вычислено:

Загрузка … пожалуйста подождите!
Это займет несколько секунд.

Это не то, что Вы имели ввиду? Используйте скобки! В случае необходимости, выберите переменную и пределы интегрирования в разделе «Настройки«.

Поддержка

Вам помог мой калькулятор? Расскажите своим друзьям об этом Калькуляторе и Вы тоже сможете мне помочь!

Результаты вычислений

Как работает Калькулятор Интегралов

Для тех кому интересны технические подробности, в этой части рассказывается как устроен и работает Калькулятор Интегралов.

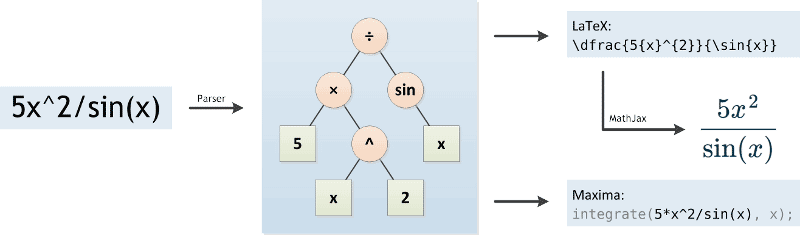
Сначала синтаксический анализатор (па́рсер) анализирует исходное математическое выражение. Он преобразует его в форму более удобную для компьютера, а именно в форму дерева (см. картинку ниже). В процессе такого преобразования, Интегральный Калькулятор должен соблюдать порядок операций с учетом их приоритета. Так же, как и то, что в математических выражениях знак умножения часто опускается, например, мы обычно пишем «5x» вместо «5*x». Калькулятор Интегралов должен уметь понимать такие случаи и сам добавлять знак умножения.

Па́рсер написан на JavaScript, и основывается на алгоритме сортировочной станции, поэтому может исполняться прямо в браузере. Это дает возможность генерировать удобочитаемое выражение на ходу, преобразуя получающееся дерево в код для LaTeX (Ла́тех). С помощью MathJax происходит генерация картинки и ее отображение в браузере.

По нажатию кнопки «=», Калькулятор Интегралов отправляет математическое выражение вместе с параметрами (переменной интегрирования и пределами интегрирования) на сервер, где оно анализируется еще раз. В этот раз выражение преобразуется в форму которая будет понятна системе компьютерной алгебры Maxima (Ма́ксима).

Ма́ксима вычисляет интеграл математической функции. Результат Ма́ксимы снова преобразуется в Ла́тех а затем показывается пользователю. Первообразная вычисляется с помощью алгоритма Ри́ша, который достаточно замысловат для понимания человеком. Именно поэтому задача показывать промежуточные шаги решения интегралов является такой сложной.

Для того чтобы всё-таки показать пошаговое решение, Калькулятор Интегралов использует такие же методы, которыми бы воспользовался человек. Алгоритм, который это осуществляет, разрабатывался в течении нескольких лет и был написан на собственном языке программирования Ма́ксимы. Программа содержит более чем 17000 строк кода. Если интегрируемое выражение совпадает по форме с уже известным, алгоритм применяет заранее определённые правила для решения интеграла (например, метод неопределённых коэффициентов для рациональных функций, тригонометрическую подстановку в интегралах с квадратным корнем из квадратичной функции или интегрирование по частям для продуктов определенных функций). Если же оно не совпадает с уже известным, тогда алгоритм пробует разные подстановки и преобразования пока интеграл не будет решен или пока не закончится отведённое для этого время или же пока не кончатся все возможные варианты. С одной стороны, у Калькулятора нет математической интуиции, которая бы очень помогла в поисках первообразной, но зато, с другой стороны, Калькулятор в состоянии перепробовать большое количество разных вариантов за очень короткое время. Такое пошаговое вычисление первообразной по правилам, зачастую, более компактно и элегантно чем вычисленное Ма́ксимой.

Еще один режим работы «Проверка решения» должен решить сложную задачу по определению являются ли два математических выражения равными друг другу. Разница между выражениями вычисляется и упрощается с помощью Ма́ксимы настолько, насколько это возможно. К примеру, это может быть переписывание тригонометрических/гиперболических функций в их экспоненциальные формы. Если удается упростить разницу до нуля — задача выполнена. В противном случае, применяется вероятностный алгоритм, который вычисляет и сравнивает оба выражения в случайно выбранных местах. В случае с первообразной, вся процедура повторяется для каждой производной, т.к. первообразная может отличаться константой.

Интерактивные графики функций вычисляются в браузере и отрисовываются на Сanvas («Холст») из HTML5. Для каждой математической функции, которая должна быть отрисована, Калькулятор создает функцию JavaScript, которая затем вычисляется с шагом, необходимым для правильного отображения графика. Все сингулярности (например полюса) функции обнаруживаются в процессе отрисовки и обрабатываются отдельно. Управление жестами для мобильных устройств сделано на основе hammer.js.

Если у Вас есть вопросы или пожелания, а так же идеи как улучшить Калькулятор Интегралов, пожалуйста пишите мне на e-mail.