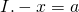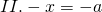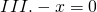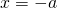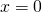Как решить уравнение с минусом

Почему минус на минус всегда даёт плюс?

Польза натуральных чисел

Для начала немного окунёмся в историю арифметики. Совершенно естественно, что в самом начале люди пользовались только натуральными числами — один, два, три и так далее. Их использовали для того, чтобы посчитать реальное количество предметов. Просто так, в отрыве от всего, цифры были бесполезны, поэтому стали появляться и действия, с помощью которых стало возможно оперировать числами. Абсолютно логично, что самым необходимым для человека стало сложение. Эта операция проста и естественна — подсчитать количество предметов становилось проще, теперь не нужно было каждый раз считать заново — «один, два, три». Заменить счёт теперь стало возможным с помощью действия «один плюс два равно три». Натуральные числа складывались, ответ тоже был натуральным числом.

Умножение представляло собой, по сути, такое же сложение. На практике мы и сейчас, например, совершая покупки, так же используем сложение и умножение, как это делали давным-давно наши предки. Однако порой приходилось совершать операции вычитания и деления. И числа не всегда были равнозначны — иногда число, от которого отнимали, было меньше числа, которое вычитали. То же и с делением. Таким образом и появились дробные числа.

Появление отрицательных чисел

В документах Индии записи об отрицательных числах появились в VII веке нашей эры. В китайских документах существуют более древние отметки об этом математическом «факте».

В жизни мы чаще всего отнимаем от большего числа меньшее. Например: у меня есть 100 рублей, хлеб и молоко стоят 65 рублей; 100 — 65 = 35 рублей сдачи. Если же я захочу купить ещё какой-то товар, стоимость которого превышает мои оставшиеся 35 рублей, например ещё одно молоко, то как бы я ни хотел его приобрести, а больше денег у меня нет, следовательно, отрицательные числа мне ни к чему.

Однако, продолжая говорить о современной жизни, упомянем кредитные карты или возможность от мобильного оператора «входить в минус» при звонках. Появляется возможность тратить большую сумму денег, чем имеешь, но те деньги, что ты остался должен, не исчезают, а записываются в долг. И вот здесь уже приходят на помощь отрицательные числа: на карте есть 100 рублей, хлеб и два молока обойдутся мне в 110 рублей; после покупки мой баланс по карте составляет -10 рублей.

Практически для таких же целей и начали впервые использовать отрицательные числа. Китайцы первыми использовали их для записи долгов или в промежуточных решениях уравнений. Но использование это было всё равно лишь для того, чтоб прийти к положительному числу (впрочем, как и наше погашение кредитки). Долгому отвержению отрицательных чисел способствовало то, что они не выражали конкретных предметов. Десять монет — это десять монет, вот они, их можно потрогать, на них можно купить товар. А что значит «минус десять монет»? Они предполагаются, даже если это долг. Неизвестно, вернётся ли этот долг, и превратятся ли «записанные» монеты в реальные. Если при решении какой-нибудь задачи получалось отрицательное число, считалось, что вышел неверный ответ или ответа вообще не существует. Такое недоверчивое отношение сохранялось у людей достаточно долго, даже Декарт (XVII век), совершивший прорыв в математике, считал отрицательные числа «ложными».

Формирование правил действий с отрицательными числами

Рассмотрим уравнение 9х-12=4х-2. Для решения уравнения нужно перенести члены с неизвестным в одну сторону, а известные числа — в другую. Это можно выполнить двумя способами.

Переносим часть уравнения с неизвестным в левую сторону, а другие числа — в правую. Получается:

Ответ найден. За все действия, что нам потребовалось выполнить, мы ни разу не прибегнули к использованию отрицательных чисел.

Теперь переносим часть уравнения с неизвестным в правую сторону, а остальные слагаемые — в левую. Получаем:

Чтобы найти решение, нам нужно одно отрицательное число разделить на другое. Однако верный ответ мы уже получили в предыдущем решении — это х, равное двум. Следовательно, остаётся вывести, что (-10)/(-5)=2.

Что доказывают нам эти два способа решения одного уравнения? Первое, что становится ясно – это то, каким образом выводилась адекватность оперирования отрицательными числами — полученный ответ должен быть таким же, что и при решении с использованием только натуральных чисел. Второй момент — это тот факт, что не нужно больше задумываться над величинами, чтобы получать непременно неотрицательное число. Можно выбирать наиболее удобный способ решения, особенно это касается сложных уравнений. Действия, которые позволили не задумываться над некоторыми операциями (что нужно сделать, чтоб были только натуральные числа; какое число больше, чтоб вычитать именно от него и т.д.), стали первыми шагами к «абстракцианизации» математики.

Естественно, не все правила действий с отрицательными числами сформировались единовременно. Копились решения, обобщались примеры, на основе чего и стали понемногу «вырисовывать» основные аксиомы. С развитием математики, с выделением новых правил, появлялись новые уровни абстракции. Например, в девятнадцатом веке стало доказано, что целые числа и многочлены имеют много общего, хотя внешне отличаются. Все их можно складывать, вычитать и перемножать. Правила, которым они подчиняются, влияют на них одним образом. Что же касается деления одних целых чисел на другие, то здесь «поджидает» занимательный факт — ответом не всегда будет целое число. Этот же закон распространяется и на многочлены.

Затем было выявлено множество других совокупностей математических объектов, над которыми возможно было производить такие операции: формальные степенные ряды, непрерывные функции. Со временем математики установили, что после исследования свойств операций результаты станет возможно применять ко всем этим совокупностям объектов. Точно так же работают и в современной математике.

Больше интересных материалов:

Сугубо математический подход

С течением времени математики выявили новый термин — кольцо. Под кольцом подразумевают множество элементов и операции, которые можно над ними производить. Основополагающими становятся правила (те самые аксиомы), которым подчиняются действия, а не природа элементов множества. Для того, чтоб выделить первостепенность структуры, возникающую после введения аксиом, как раз обычно и употребляют термин «кольцо»: кольцо целых чисел, кольцо многочленов и т. п. Используя аксиомы и исходя из них, можно выявлять новые свойства колец.

Сформулируем правила кольца, похожие на аксиомы операций с целыми числами, и докажем, что в любом кольце при умножении минуса на минус выходит плюс.

Под кольцом понимается множество с двумя бинарными операциями (в каждом действии участвуют два элемента кольца), традиционно именуемыми сложением и умножением, и следующими аксиомами:

— сложение элементов кольца подчиняется переместительному (A + B = B + A для любых элементов A и B) и сочетательному (A + (B + C) = (A + B) + C) законам; в кольце есть специальный элемент 0 (нейтральный элемент по сложению) такой, что A + 0 = A, и для любого элемента A есть противоположный элемент (обозначаемый (—A)), что A + (—A) = 0;

— умножение подчиняется сочетательному закону: A · (B · C) = (A · B) · C;

— сложение и умножение связаны следующими правилами раскрытия скобок:

(A + B) · C = A · C + B · C

A · (B + C) = A · B + A · C.

Уточним, что кольца, в самой общей конструкции, не требуют ни перестановочности умножения, ни его обратимости (операция деления не всегда возможна), ни существования единицы — нейтрального элемента по умножению. Если ввести данные аксиомы, получим другие алгебраические структуры, однако со всеми действующими теоремами, доказанными для колец.

Следующим этапом станет доказательство того, что для любых элементов A и B произвольного кольца верно: (-A) · B = -(A · B) и (-(-A)) = A.

Из этого получим утверждения про единицы:

Далее следует доказать некоторые моменты. Во-первых, нужно установить существование лишь одной противоположности для каждого элемента. Допустим, наличие у элемента А два противоположных элемента: B и С. То есть A + B = 0 = A + C. Разберём сумму A + B + C. Используя переместительный и сочетательный законы, а также свойства нуля, получим, что сумма равна:

B: B = B + 0 = B + (A + C) = A + B + C

C: A + B + C = (A + B) + C = 0 + C = C.

Следовательно, B = C.

Отметим, что и A, и (-(-A)) противоположны к элементу (-A). Отсюда заключаем, что элементы A и (-(-A)) должны быть равны.

Далее, 0 = 0 · B = (A + (-A)) · B = A · B + (-A) · B,

т.е. (-A) · B противоположно A · B, следовательно, оно равно -(A · B).

Заметим, что 0 · B = 0 для любого элемента B.

0·B = (0 + 0) B = 0·B + 0·B,

таким образом, прибавление 0·B не изменяет сумму. Получается, это произведение равно нулю.

Уравнения вида -х равен a

Уравнения вида «-x равен а» появляются в 6 классе с началом изучения отрицательных чисел.

Поскольку такие уравнения в дальнейшем будут встречаться довольно часто, желательно сразу же научиться их решать правильно и быстро.

В общем виде уравнения вида «минус икс равен а» можно разбить на три случая:

Рассмотрим каждый из вариантов в общем виде и на примерах.

Решить это уравнение — значит, найти x. x и -x — противоположные числа. Поэтому икс равен числу, противоположному числу, стоящему в правой части уравнения, то есть числу которое отличается только знаком:

Рассуждая аналогично, приходим к выводу, что

Здесь минус икс равен нулю. Нуль не является ни положительным, ни отрицательным числом и противоположен самому себе, поэтому корень этого уравнения

Итак, в общем виде решение уравнений вида минус икс равен а можно записать так:

Как объяснить уравнения с х (икс) школьнику в 4 классе?

Автор: Творческая Анна

Недавно звонит мама школьника, с которым я занимаюсь и просит объяснить математику ребёнку, т.к он не понимает, а она не него кричит и разговор с сыном не выходит.

У меня не математический склад ума, творческим людям это не свойственно, но я сказала, что посмотрю что они проходят и попробую. И вот что получилось.

Я взяла лист бумаги формата А4, обычный белый, фломастеры, карандаш в руки и начала выделять, то что стоит понять, запомнить, обратить внимание. И чтобы было видно, куда эта цифра переходит и как меняется.

Объяснение примеров с левой стороны, на правую сторону.

Пример № 1

Пример уравнения для 4 класса со знаком плюс.

Самым первым действием смотрим, что мы можем сделать в этом уравнении? Тут мы можем выполнить умножение. Умножаем 80*7 получаем 560. Переписываем ещё раз.

Х + 320 = 560 (выделила цифры зеленым маркером).

Теперь мы видим, что у нас есть х (неизвестное) и числа, только не рядом, а разделяет их знак равно. Х в одну сторону, цифры в другую.

Х = 560 – 320. Минус ставим потому что при переносе числа, знак что перед ним меняется на противоположный. Выполняем вычитание.

Х = 240 Обязательно делаем проверку. Проверка покажет правильно ли мы решили уравнение. Вместо х вставляем число, которое получили.

Проверка:

240 + 320 = 80*7 Складываем числа, с другой стороны умножаем.

Всё верно! Значит мы решили уравнение правильно!

Пример № 2

Пример уравнения для 4 класса со знаком минус.

Первым действием смотрим, что мы можем сделать в этом уравнении? В данном примере мы можем разделить. Производим деление 240 разделить на 3 получаем 80. Переписываем уравнение ещё раз.

Х – 180 = 80 (выделила цифры зеленым маркером).

Теперь мы видим, что у нас есть х (неизвестное) и числа, только не рядом, а разделяет их знак равно. Х в одну сторону, цифры в другую.

Х = 80 + 180 Знак плюс ставим потому что при переносе числа, знак что был перед цифрой меняется на противоположный. Считаем.

Х = 260 Выполняем проверочную работу. Проверка покажет правильно ли мы решили уравнение. Вместо х вставляем число, которое получили.

Проверка:

Пример № 3

Пример уравнения для 4 класса со знаком минус, где х в середине, другими словами пример уравнения, где х отрицательный в середине.

400 – х = 275 + 25 Складываем числа.

400 – х = 300 Числа разделены знаком равенства, х является отрицательным. Чтобы сделать его положительным, нам нужно перенести его через знак равно, собираем числа в одной стороне, х в другой.

400 — 300 = х Цифра 300 была положительной, при переносе в другую сторону поменяла знак и стал минус. Считаем.

Т.к не принято так писать, а первым в уравнении должен быть х, просто меняем их местами.

Проверка:

400 – 100 = 275 + 25 Считаем.

Пример № 4

Пример уравнения для 4 класса со знаком минус, где х в середине, другими словами пример уравнения, где х отрицательный в середине.

72 – х = 18 * 3 Выполняем умножение. Переписываем пример.

72 – х = 54 Выстраиваем числа в одну сторону, х в другую. Цифра 54 меняет знак на противоположный, т.к перепрыгивает через знак равно.

72 – 54 = х Считаем.

18 = х Меняем местами, для удобства.

Проверка:

Пример № 5

Пример уравнения с х с вычитанием и сложением для 4 класса.

Х – 290 = 470 + 230 Складываем.

Х – 290 = 700 Выставляем числа с одной стороны.

Х = 700 + 290 Считаем.

Проверка:

990 – 290 = 470 + 230 Выполняем сложение.

Пример № 6

Пример уравнения с х на умножение и деление для 4 класса.

15 * х = 630/70 Выполняем деление. Переписываем уравнение.

15 * х = 90 Это тоже самое, что 15х = 90 Оставляем х с одной стороны, числа с другой. Данное уравнение принимает следующий вид.

Х = 90/15 при переносе цифры 15 знак умножения меняется на деление. Считаем.

Проверка:

15*6 = 630 / 7 Выполняем умножение и вычитание.

Теперь озвучиваем основные правила:

1. Умножаем, складываем, делим или вычитаем;

Выполняем то, что можно сделать, уравнение станет немного короче.

Х в одну сторону, цифры в другую.

Неизвестную переменную в одну сторону (не всегда это х, может быть и другая буква), числа в другую.

При переносе х или цифры через знак равенства, их знак меняется на противоположный.

Если было число положительным, то при переносе перед цифрой ставим знак минус. И наоборот, если число или х было со знаком минус, то при переносе через равно ставим знак плюс.

При выполнении домашнего задания, классной работы, тестов, всегда можно взять лист и написать вначале на нём и сделать проверку.

Дополнительно находим подобные примеры в интернете, дополнительных книгах, методичках. Проще не менять цифры, а брать уже готовые примеры.

Чем больше ребёнок будет решать сам, заниматься самостоятельно, тем быстрее усвоит материал.

Если ребенок не понимает примеры с уравнением, стоит объяснить пример и сказать, чтобы остальные делал по образцу.

Данное подробное описание, как объяснить уравнения с х школьнику для:

• родителей;
• школьников;
• репетиторов;
• бабушек и дедушек;
• учителей;

Детям нужно все делать в цвете, разными мелками на доске, но увы не все так делают.

Из своей практики

Мальчик писал так, как хотел, вопреки существующим правилам по математике. При проверке уравнения были разные цифры и одно число (с левой стороны) не равнялось другому (то что с правой стороны), он тратил время на поиски ошибки.

При вопросе, почему он так делает? Был ответ, что он пытается угадать и думает, а вдруг сделает правильно.

В данном случае нужно каждый день (через день) решать подобные примеры. Довести действия до автоматизма и конечно все дети разные, дойти может не с первого занятия.

Если у родителей нет времени, а часто это так, потому что родители зарабатывают денежные средства, то лучше найти репетитора в своём городе, который сможет объяснить пройденный материал ребёнку.

Сейчас век ЕГЭ, тестов, контрольных работ, есть дополнительные сборники и методички. Делая за ребёнка домашние задания, родители должны помнить, что на экзамене в школе их не будет. Лучше объяснить доходчиво ребёнку 1 раз, чтобы ребёнок смог самостоятельно решать примеры.