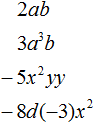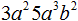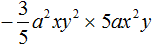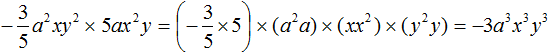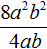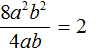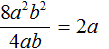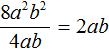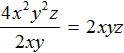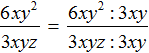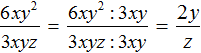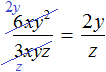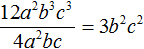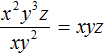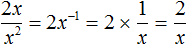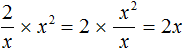Как решить уравнение с одночленами

Одночлены

Определения и примеры

Одночлен — это произведение чисел, переменных и степеней. Например, выражения 5a , 3ab 2 и −6 2 aa 2 b 3 являются одночленами.

Приведём ещё примеры одночленов:

Одночленом также является любое отдельное число, любая переменная или любая степень. Например, число 9 является одночленом, переменная x является одночленом, степень 5 2 является одночленом.

Приведение одночлена к стандартному виду

Рассмотрим следующий одночлен:

Этот одночлен выглядит не очень аккуратно. Чтобы сделать его проще, нужно привести его к так называемому стандартному виду.

Приведение одночлена к стандартному виду заключается в перемножении однотипных сомножителей, входящих в этот одночлен. То есть числа нужно перемножать с числами, переменные с переменными, степени со степенями. В результате этих действий получается упрощённый одночлен, который тождественно равен предыдущему.

Ещё один нюанс заключается в том, что в одночлене степени можно перемножать только в том случае, если они имеют одинаковые основания.

Итак, приведём одночлен 3a 2 5a 3 b 2 к стандартному виду. В этом одночлене содержатся числа 3 и 5. Перемножим их, получим число 15. Записываем его:

Далее в одночлене 3a 2 5a 3 b 2 содержатся степени a 2 и a 3 , которые имеют одинаковое основание a . Из тождественных преобразований со степенями известно, что при перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают. Тогда перемножение степеней a 2 и a 3 даст в результате a 5 . Записываем a 5 рядом с числом 15

Далее в одночлене 3a 2 5a 3 b 2 содержится степень b 2 . Её не с чем перемножать, поэтому она остаётся без изменений. Записываем её как есть к новому одночлену:

Мы привели одночлен 3a 2 5a 3 b 2 к стандартному виду. В результате получили одночлен 15a 5 b 2

Числовой сомножитель 15 называют коэффициентом одночлена. Приводя одночлен к стандартному виду, коэффициент нужно записывать в первую очередь, и только потом переменные и степени.

Если коэффициент в одночлене отсутствует, то говорят, что коэффициент равен единице. Так, коэффициентом одночлена abc является 1, поскольку abc это произведение единицы и abc

А коэффициентом одночлена −abc будет −1 , поскольку −abc это произведение минус единицы и abc

Степенью одночлена называют сумму показателей всех переменных входящих в этот одночлен.

Например, степенью одночлена 15a 5 b 2 является 7 . Это потому что переменная a имеет показатель 5, а переменная b имеет показатель 2. Отсюда 5 + 2 = 7 . Показатель числового сомножителя 15 считать не нужно, поскольку нас интересуют только показатели переменных.

Ещё пример. Степенью одночлена 7ab 2 является 3. Здесь переменная a имеет показатель 1, а переменная b имеет показатель 2. Отсюда 1 + 2 = 3 .

Если одночлен не содержит переменных или степеней, а состоит из числа, то говорят, что степень такого одночлена равна нулю. Например, степень одночлена 11 равна нулю.

Не следует путать степень одночлена и степень числа. Степень числа это произведение из нескольких одинаковых множителей, тогда как степень одночлена это сумма показателей всех переменных входящих в этот одночлен. В одночлене 11 нет переменных, поэтому его степень равна нулю.

Пример 1. Привести одночлен 5xx3ya 2 к стандартному виду

Перемножим числа 5 и 3, получим 15. Это будет коэффициент одночлена:

Далее в одночлене 5xx3ya 2 содержатся переменные x и x . Перемножим их, получим x 2 .

Далее в одночлене 5xx3ya 2 содержится переменная y , которую не с чем перемножать. Записываем её без изменений:

Далее в одночлене 5xx3ya 2 содержится степень a 2 , которую тоже не с чем перемножать. Её также оставляем без изменений:

Получили одночлен 15x 2 ya 2 , который приведён к стандартному виду. Буквенные сомножители принято записывать в алфавитном порядке. Тогда одночлен 15x 2 ya 2 примет вид 15a 2 x 2 y.

Пример 2. Привести одночлен 2m 3 n × 0,4mn к стандартному виду

Перемножим числа, переменные и степени по отдельности.

Числа, переменные и степени при перемножении разрешается заключать в скобки. Делается это для удобства. Так, в данном примере перемножение чисел 2 и 0,4 можно заключить в скобки. Также в скобки можно заключить перемножение m 3 × m и n × n

Но желательно выполнять все элементарные действия в уме. Так, решение можно записать значительно короче:

Но чтобы в уме приводить одночлен к стандартному виду, тема умножения целых чисел и умножения степеней должна быть изучена на хорошем уровне.

Сложение и вычитание одночленов

Одночлены можно складывать и вычитать. Чтобы это было возможно, они должны иметь одинаковую буквенную часть. Коэффициенты могут быть любыми. Сложение и вычитание одночленов это по сути приведение подобных слагаемых, которое мы рассматривали при изучении буквенных выражений.

Чтобы сложить (вычесть) одночлены, нужно сложить (вычесть) их коэффициенты, а буквенную часть оставить без изменений.

Пример 1. Сложить одночлены 6a 2 b и 2a 2 b

Сложим коэффициенты 6 и 2, а буквенную часть 6a 2 b оставим без изменений

Пример 2. Вычесть из одночлена 5a 2 b 3 одночлен 2a 2 b 3

Можно заменить вычитание сложением, и сложить коэффициенты одночленов, оставив буквенную часть без изменения:

Либо сразу из коэффициента первого одночлена вычесть коэффициент второго одночлена, а буквенную часть оставить без изменения:

Умножение одночленов

Одночлены можно перемножать. Чтобы перемножить одночлены, нужно перемножить их числовые и буквенные части.

Пример 1. Перемножить одночлены 5x и 8y

Перемножим числовые и буквенные части по отдельности. Для удобства перемножаемые сомножители будем заключать в скобки:

Пример 2. Перемножить одночлены 5x 2 y 3 и 7x 3 y 2 c

Перемножим числовые и буквенные части по отдельности. В процессе умножения будем применять правило перемножения степеней с одинаковыми основаниями. Перемножаемые сомножители будем заключать в скобки:

Пример 3. Перемножить одночлены −5a 2 bc и 2a 2 b 4

Пример 4. Перемножить одночлены x 2 y 5 и (−6xy 2 )

Пример 5. Найти значение выражения

Деление одночленов

Одночлен можно разделить на другой одночлен. Для этого нужно коэффициент первого одночлена разделить на коэффициент второго одночлена, а буквенную часть первого одночлена разделить на буквенную часть второго одночлена. При этом используется правило деления степеней.

Например, разделим одночлен 8a 2 b 2 на одночлен 4ab. Запишем это деление в виде дроби:

Первый одночлен 8a 2 b 2 будем называть делимым, а второй 4ab — делителем. А одночлен, который получится в результате, назовём частным.

Разделим коэффициент делимого на коэффициент делителя, получим 8 : 4 = 2 . В исходном выражении ставим знак равенства и записываем этот коэффициент частного:

Теперь делим буквенную часть. В делимом содержится a 2 , в делителе — просто a . Делим a 2 на a , получаем a , поскольку a 2 : a = a 2 − 1 = a . Записываем в частном a после 2

Далее в делимом содержится b 2 , в делителе — просто b . Делим b 2 на b , получаем b , поскольку b 2 : b = b 2 − 1 = b . Записываем в частном b после a

Значит, при делении одночлена 8a 2 b 2 на одночлен 4ab получается одночлен 2ab .

Сразу можно выполнить проверку. При умножении частного на делитель должно получаться делимое. В нашем случае, если 2ab умножить на 4ab , должно получиться 8a 2 b 2

Не всегда можно первый одночлен разделить на второй одночлен. Например, если в делителе окажется переменная, которой нет в делимом, то говорят, что деление невозможно.

К примеру, одночлен 6xy 2 нельзя разделить на одночлен 3xyz . В делителе 3xyz содержится переменная z , которая не содержится в делимом 6xy 2 .

Проще говоря, мы не сможем найти частное, которое при умножении на делитель 3xyz дало бы делимое 6xy 2 , поскольку такое умножение обязательно будет содержать переменную z, которой нет в 6xy 2 .

Но если в делимом содержится переменная, которая не содержится в делителе, то деление будет возможным. В этом случае переменная, которая отсутствовала в делителе, будет перенесена в частное без изменений.

Например, при делении одночлена 4x 2 y 2 z на 2xy , получается 2xyz . Сначала разделили 4 на 2 получили 2, затем x 2 разделили на x , получили x , затем y 2 разделили на y , получили y. Затем приступили к делению переменной z на такую же переменную в делителе, но обнаружили, что такой переменной в делителе нет. Поэтому перенесли переменную z в частное без изменений:

Для проверки умножим частное 2xyz на делитель 2xy . В результате должен получиться одночлен 4x 2 y 2 z

Но в некоторых дробях, если невозможно выполнить деление, бывает возможным выполнить сокращение. Делается это с целью упростить выражение.

Так, в предыдущем примере нельзя было разделить одночлен 6xy 2 на одночлен 3 xyz . Но можно сократить эту дробь на одночлен 3xy . Напомним, что сокращение дроби это деление числителя и знаменателя на одно и то же число (в нашем случае на одночлен 3 xy ). В результате сокращения дробь становится проще, но её значение не меняется:

В числителе и знаменателе мы пришли к делению одночленов, которое можно выполнить:

Процесс деления обычно выполняется в уме, записывая над числителем и знаменателем получившийся результат:

Пример 2. Разделить одночлен 12a 2 b 3 c 3 на одночлен 4a 2 bc

Пример 3. Разделить одночлен x 2 y 3 z на одночлен xy 2

Дополнительно упомянем, что деление одночлена на одночлен также невозможно, если одна из степеней, входящая в делимое, имеет показатель меньший, чем показатель той же степени из делителя.

Например, разделить одночлен 2x на одночлен x 2 нельзя, поскольку степень x , входящая в делимое, имеет показатель 1, тогда как степень x 2 , входящая в делитель, имеет показатель 2. Мы не сможем найти частное, которое при перемножении с делителем x 2 даст в результате делимое 2x .

Конечно, мы можем выполнить деление x на x 2 , воспользовавшись свойством степени с целым показателем:

и такое частное при перемножении с делителем x 2 будет давать в результате делимое 2x

Но нас пока интересуют только те частные, которые являются так называемыми целыми выражениями. Целые выражения это те выражения, которые не являются дробями, в знаменателе которых содержится буквенное выражение. А частное 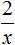целым выражением не является. Это дробное выражение, в знаменателе которого содержится буквенное выражение.

Возведение одночлена в степень

Одночлен можно возвести в степень. Для этого используют правило возведения степени в степень.

Пример 1. Возвести одночлен xy во вторую степень.

Чтобы возвести одночлен xy во вторую степень, нужно возвести во вторую степень каждый сомножитель этого одночлена

Пример 2. Возвести одночлен −5a 3 b во вторую степень.

Пример 3. Возвести одночлен − a 2 bc 3 в пятую степень.

В данном примере коэффициентом одночлена является −1. Этот коэффициент тоже нужно возвести в пятую степень:

Когда коэффициент равен −1, то саму единицу не записывают. Записывают только минус и потом остальные сомножители одночлена. В приведенном примере сначала получился одночлен −1a 10 b 5 c 15 , затем он был заменён на тождественно равный ему одночлен −a 10 b 5 c 15 .

Пример 4. Представить одночлен 4x 2 в виде одночлена, возведённого в квадрат.

В данном примере нужно найти произведение, которое во второй степени будет равно выражению 4x 2 . Очевидно, что это произведение 2x. Если это произведение возвести во вторую степень (в квадрат), то получится 4x 2

Значит, 4x 2 = (2x) 2 . Выражение (2x) 2 это и есть одночлен, возведённый в квадрат.

Пример 5. Представить одночлен 121a 6 в виде одночлена, возведённого в квадрат.

Попробуем найти произведение, которое во второй степени будет равно выражению 121a 6 .

Прежде всего заметим, что число 121 получается, если число 11 возвести в квадрат. То есть первый сомножитель будущего произведения мы нашли. А степень a 6 получается в том случае, если возвести в квадрат степень a 3 . Значит вторым сомножителем будущего произведения будет a 3 .

Таким образом, если произведение 11a 3 возвести во вторую степень, то получится 121a 6

(11a 3 ) 2 = 11 2 × (a 3 ) 2 = 121a 6

Значит, 121a 6 = (11a 3 ) 2 . Выражение (11a 3 ) 2 это и есть одночлен, возведённый в квадрат.

Разложение одночлена на множители

Поскольку одночлен является произведением чисел, переменных и степеней, то он может быть разложен на множители, из которых состоит.

Пример 1. Разложить одночлен 3a 3 b 2 на множители

Данный одночлен можно разложить на множители 3, a, a, a, b, b

Либо степень b 2 можно не раскладывать на множители b и b

Либо степень b 2 разложить на множители b и b , а степень a 3 оставить без изменений

В каком виде представлять одночлен зависит от решаемой задачи. Главное, чтобы разложение было тождественно равно исходному одночлену.

Пример 2. Разложить одночлен 10a 2 b 3 c 4 на множители.

Разложим коэффициент 10 на множители 2 и 5, степень a 2 разложим на множители aa , степень b 3 — на множители bbb , степень c 4 — на множители cccc

Действия с одночленами

В предыдущей статье мы рассказали, что из себя представляют одночлены. В этом материале разберем, как решать примеры и задачи, в которых они применяются. Здесь будут рассмотрены такие действия, как вычитание, сложение, умножение, деление одночленов и возведение их в степень с натуральным показателем. Мы покажем, как определяются такие операции, обозначим основные правила их выполнения и то, что должно получится в результате. Все теоретические положения, как обычно, будут проиллюстрированы примерами задач с описаниями решений.

Удобнее всего работать со стандартной записью одночленов, поэтому все выражения, которые будут использованы в статье, мы приводим в стандартном виде. Если изначально они заданы иначе, рекомендуется сначала привести их к общепринятой форме.

Правила сложения и вычитания одночленов

Наиболее простые действия, которые можно проводить с одночленами – это вычитание и сложение. В общем случае результатом этих действий будет являться многочлен (одночлен возможен в некоторых частных случаях).

Когда мы складываем или вычитаем одночлены, сначала записываем в общепринятой форме соответствующую сумму и разность, после чего упрощаем получившееся выражение. Если есть подобные слагаемые, их нужно привести, скобки – раскрыть. Поясним на примере.

Условие: выполните сложение одночленов − 3 · x и 2 , 72 · x 3 · y 5 · z .

Запишем сумму исходных выражений. Добавим скобки и поставим между ними плюс. У нас получится следующее:

( − 3 · x ) + ( 2 , 72 · x 3 · y 5 · z )

Когда мы выполним раскрытие скобок, получится — 3 · x + 2 , 72 · x 3 · y 5 · z . Это многочлен, записанный в стандартной форме, который и будет результатом сложения данных одночленов.

Ответ: ( − 3 · x ) + ( 2 , 72 · x 3 · y 5 · z ) = − 3 · x + 2 , 72 · x 3 · y 5 · z .

Если у нас задано три, четыре и больше слагаемых, мы осуществляем это действие точно так же.

Условие: проведите в правильном порядке указанные действия с многочленами

3 · a 2 — ( — 4 · a · c ) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c

Начнем с раскрытия скобок.

3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c

Мы видим, что полученное выражение можно упростить путем приведения подобных слагаемых:

3 · a 2 + 4 · a · c + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = = ( 3 · a 2 + a 2 — 7 · a 2 ) + 4 · a · c — 2 2 3 · a · c + 4 9 = = — 3 · a 2 + 1 1 3 · a · c + 4 9

У нас получился многочлен, который и будет результатом данного действия.

Ответ: 3 · a 2 — ( — 4 · a · c ) + a 2 — 7 · a 2 + 4 9 — 2 2 3 · a · c = — 3 · a 2 + 1 1 3 · a · c + 4 9

В принципе, мы можем выполнить сложение и вычитание двух одночленов с некоторыми ограничениями так, чтобы получить в итоге одночлен. Для этого нужно соблюсти некоторые условия, касающиеся слагаемых и вычитаемых одночленов. О том, как это делается, мы расскажем в отдельной статье.

Правила умножения одночленов

Действие умножения не налагает никаких ограничений на множители. Умножаемые одночлены не должны соответствовать никаким дополнительным условиям, чтобы в результате получится одночлен.

Чтобы выполнить умножение одночленов, нужно выполнить следующие шаги:

1. Правильно записать произведение.
2. Раскрыть скобки в полученном выражении.
3. Сгруппировать по возможности множители с одинаковыми переменными и числовые множители отдельно.
4. Выполнить необходимые действия с числами и применить к оставшимся множителям свойство умножения степеней с одинаковыми основаниями.

Посмотрим, как это делается на практике.

Условие: выполните умножение одночленов 2 · x 4 · y · z и — 7 16 · t 2 · x 2 · z 11 .

Начнем с составления произведения.

2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11

Раскрываем в нем скобки и получаем следующее:

2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11

Далее нам нужно объединить числовые множители в одну группу, а потом сгруппировать множители с одинаковыми переменными:

2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11

Все, что нам осталось сделать – это умножить числа в первых скобках и применить свойство степеней для вторых. В итоге получим следующее:

2 · — 7 16 · t 2 · x 4 · x 2 · y · z 3 · z 11 = — 7 8 · t 2 · x 4 + 2 · y · z 3 + 11 = = — 7 8 · t 2 · x 6 · y · z 14

Ответ: 2 · x 4 · y · z · — 7 16 · t 2 · x 2 · z 11 = — 7 8 · t 2 · x 6 · y · z 14 .

Если у нас в условии стоят три многочлена и больше, мы умножаем их по точно такому же алгоритму. Более подробно вопрос умножения одночленов мы рассмотрим в рамках отдельного материала.

Правила возведения одночлена в степень

Мы знаем, что степенью с натуральным показателем называют произведение некоторого числа одинаковых множителей. На их количество указывает число в показателе. Согласно этому определению, возведение одночлена в степень равнозначно умножению указанного числа одинаковых одночленов. Посмотрим, как это делается.

Условие: выполните возведение одночлена − 2 · a · b 4 в степень 3 .

Мы можем заменить возведение в степень на умножение 3 -х одночленов − 2 · a · b 4 . Запишем и получим нужный ответ:

( − 2 · a · b 4 ) 3 = ( − 2 · a · b 4 ) · ( − 2 · a · b 4 ) · ( − 2 · a · b 4 ) = = ( ( − 2 ) · ( − 2 ) · ( − 2 ) ) · ( a · a · a ) · ( b 4 · b 4 · b 4 ) = − 8 · a 3 · b 12

Ответ: ( − 2 · a · b 4 ) 3 = − 8 · a 3 · b 12 .

А как быть в том случае, когда степень имеет большой показатель? Записывать большое количество множителей неудобно. Тогда для решения такой задачи нам надо применить свойства степени, а именно свойство степени произведения и свойство степени в степени.

Решим задачу, которую мы привели выше, указанным способом.

Условие: выполните возведение − 2 · a · b 4 в третью степень.

Зная свойство степени в степени, мы можем перейти к выражению следующего вида:

( − 2 · a · b 4 ) 3 = ( − 2 ) 3 · a 3 · ( b 4 ) 3 .

После этого мы возводим в степень — 2 и применяем свойство степени в степени:

( − 2 ) 3 · ( a ) 3 · ( b 4 ) 3 = − 8 · a 3 · b 4 · 3 = − 8 · a 3 · b 12 .

Ответ: − 2 · a · b 4 = − 8 · a 3 · b 12 .

Возведению одночлена в степень мы также посвятили отдельную статью.

Правила деления одночленов

Последнее действие с одночленами, которое мы разберем в данном материале, – деление одночлена на одночлен. В результате мы должны получить рациональную (алгебраическую) дробь (в некоторых случаях возможно получение одночлена). Сразу уточним, что деление на нулевой одночлен не определяется, поскольку не определяется деление на 0.

Для выполнения деления нам нужно записать указанные одночлены в форме дроби и сократить ее, если есть такая возможность.

Условие: выполните деление одночлена − 9 · x 4 · y 3 · z 7 на − 6 · p 3 · t 5 · x 2 · y 2 .

Начнем с записи одночленов в форме дроби.

— 9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2

Эту дробь можно сократить. После выполнения этого действия получим:

3 · x 2 · y · z 7 2 · p 3 · t 5

Ответ: — 9 · x 4 · y 3 · z 7 — 6 · p 3 · t 5 · x 2 · y 2 = 3 · x 2 · y · z 7 2 · p 3 · t 5 .

Условия, при которых в результате деления одночленов мы получим одночлен, приводятся в отдельной статье.

Приведение одночлена к стандартному виду; задачи

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

В данном уроке мы вспомним, что такое одночлен и как привести его к стандартному виду. Вспомним определения коэффициента и буквенной части одночлена. Выполним задания на приведение к стандартному виду и вычисление численного значения. Научимся применять приведение одночлена к стандартному виду в различных типах задач, а именно в решении уравнений и геометрических задач с применением метода математического моделирования.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Упрощение выражений»