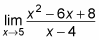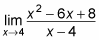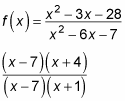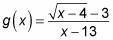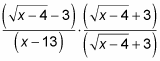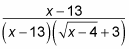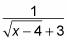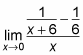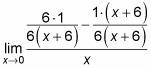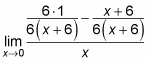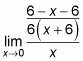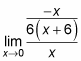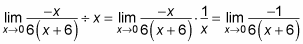Как решить уравнение с пределом

Что такое предел функции

В данной публикации мы рассмотрим одно из главных понятий математического анализа – предел функции: его определение, а также различные способы решения с практическими примерами.

Определение предела функции

Предел функции – величина, к которой стремится значение данной функции при стремлении ее аргумента к предельной для области определения точке.

Запись предела:

• предел обозначается значком lim;
• под ним добавляется, к какому значению стремится аргумент (переменная) функции. Обычно, это x , но не обязательно, например: “ x →1″;

Таким образом, финальная запись предела выглядит выглядит так (в нашем случае):

Читается как “предел функции при икс, стремящемся к единице”.

x →1 – это значит, что “икс” последовательно принимает значения, которые бесконечно приближаются к единице, но никогда с ней не совпадут (ее не достигнут).

Решение пределов

С заданным числом

Давайте решим рассмотренный выше предел. Для этого просто подставляем единицу в функцию (т.к. x →1):

Таким образом, чтобы решить предел, сперва пробуем просто подставить заданное число в функцию под ним (если икс стремится к конкретному числу).

С бесконечностью

В данному случае аргумент функции бесконечно возрастает, то есть “икс” стремится к бесконечности (∞). Например:

Если x →∞, то заданная функция стремится к минус бесконечности (-∞), т.к.:

• 3 – 1 = 2
• 3 – 10 = -7
• 3 – 100 = -97
• 3 – 1000 – 997 и т.д.

Другой более сложный пример

Для того, чтобы решить этот предел, также, просто увеличиваем значения x и смотрим на “поведение” функции при этом.

Таким образом при “икс”, стремящемся к бесконечности, функция неограниченно растет.

С неопределенностью (икс стремится к бесконечности)

В данном случае речь идет про пределы, когда функция – это дробь, числитель и знаменатель которой представляют собой многочлены. При этом “икс” стремится к бесконечности.

Пример: давайте вычислим предел ниже.

Выражения и в числителе, и а знаменателе стремятся к бесконечности. Можно предположить, что в таком случае решение будет таким:

Однако не все так просто. Чтобы решить предел нам нужно сделать следующее:

1. Находим x в старшей степени для числителя (в нашем случае – это два).

2. Аналогичным образом определяем x в старшей степени для знаменателя (тоже равняется двум).

3. Теперь делим и числитель, и знаменатель на x в старшей степени. В нашем случае в обоих случаях – во второй, но если бы они были разные, следовало бы взять наибольшую степень.

4. В получившемся результате все дроби стремятся к нулю, следовательно ответ равен 1/2.

С неопределенностью (икс стремится к конкретному числу)

И в числителе, и в знаменателе представлены многочлены, однако, “икс” стремится к конкретному числу, а не к бесконечности.

В данном случае условно закрываем глаза на то, что в знаменателе стоит ноль.

Пример: Найдем предел функции ниже.

1. Для начала подставим в функцию число 1, к которому стремится “икс”. Получаем неопределенность рассматриваемого нами вида.

2. Далее раскладываем числитель и знаменатель на множители. Для этого можно воспользоваться формулами сокращенного умножения, если они подходят, или решить квадратное уравнение.

В нашем случаем корнями выражения в числителе () являются числа 1 и 1,5. Следовательно его можно представить в виде: .

Знаменатель () изначально является простым.

3. Получаем вот такой видоизмененный предел:

4. Дробь можно сократить на ():

5. Остается только подставить число 1 в выражение, получившееся под пределом:

Предел функции.

Предел функции – число a будет пределом некоторой изменяемой величины, если в процессе своего изменения эта переменная величина неограниченно приближается к a.

Или другими словами, число A является пределом функции y = f (x) в точке x₀, если для всякой последовательности точек из области определения функции, не равных x₀, и которая сходится к точке x₀ (lim x_n = x0), последовательность соответствующих значений функции сходится к числу A.

График функции, предел которой при аргументе, который стремится к бесконечности, равен L:

Предел функции по Гейне.

Значение А является пределом (предельным значением) функции f (x) в точке x₀ в случае, если для всякой последовательности точек , которая сходится к x₀, но которая не содержит x₀ как один из своих элементов (т.е. в проколотой окрестности x₀), последовательность значений функции сходится к A.

Предел функции по Коши.

Значение A будет являться пределом функции f (x) в точке x₀ в случае, если для всякого вперёд взятого неотрицательного числа ε будет найдено соответствующее ему неотрицательно число δ = δ(ε) такое, что для каждого аргумента x, удовлетворяющего условию 0 3 , выносим в числителе и знаменателе его за скобки и далее сокращаем на него:

Ответ

Необходимо рассчитать предел

Первым шагом в нахождении этого предела, подставим значение 1 вместо x, в результате чего имеем неопределенность . Для её решения разложим числитель на множители, сделаем это методом нахождения корней квадратного уравнения x 2 + 2x — 3:

Таким образом, числитель будет таким:

Далее сокращаем числитель и знаменатель на (x – 1):

Ответ

Решение пределов функции.

Решение пределов функции — это определение его конкретного значения или определенной области, куда попадает функция, которая ограничена пределом.

Чтобы решить пределы, следуйте правилам:

1. Пробуем подставить в функцию число, результат решения и будет ответом.
2. Если х стремится не к числу, например в пределах вида или , то такие пределы решаются сразу, так как число, деленное на бесконечность, всегда дает 0, а деленное на нуль это и есть ∞. Если вам сложно понять саму суть бесконечности и нуля в пределах, то подставляйте вместо ∞ — бесконечно большое число – к примеру 1000 000, либо вместо нуля — бесконечно малое — например 0,000001 и после этого можете предположить к чему стремится ответ.
3. Существует группа пределов, в которых и в числитель, и в знаменатель при подстановке получаем либо нуль либо ∞. Это т.н. пределы с неопределенностью, часть из которых замечательные.

Разобравшись в сути и основных правилах решения предела, вы получите базовое понятие о том, как их решать.

Методы решения пределов функции

Чтобы вычислить пределы функции алгебраически, вы можете выбрать один из четырех методов: включение значения x, факторинг, рационализация числителя и поиск самого низкого общего знаменателя. Лучшим выбором является первый метод. Вы можете использовать эту технику только в том случае, если f непрерывна по значению x, в котором вы принимаете ограничение. Если f при этом не определена в значении х, вы должны перейти к другим методам, чтобы упростить вашу функцию и найти приблизительное значение для х.

Включение значения x

Первым методом алгебраического решения для нахождения f (x) является включение числа, в котором х приближается к функции. Если вы получаете неопределенное значение (0 в знаменателе или бесконечность), вы должны стремиться перейти к другому методу. Но если ваша f при этом непрерывна в значении х, вы получите значение, и все готово — вы нашли решение! Например, с помощью этого метода вы можете найти:

Пределом будет 3, так как f (5) = 3, и эта f непрерывна при х

Факторинг

Факторинг — это метод, который следует попробовать при сбое в подключении — особенно когда любая часть данной функции является полиномиальным выражением.

Если нужно выполнить это задание:

то сначала попробуйте подключить 4 к функции, и вы получите 0 в числителе и знаменателе, который говорит вам перейти к следующему методу. Квадратичное выражение в числителе говорит, чтобы вы попытались разложить его. Заметим, что числитель предыдущей функции имеет значение (х— 4) ( x — 2). Х — 4 отменяет на верхней и нижней части фракции. Этот шаг оставляет вас с f (х) = х— 2. Вы можете подключить 4 к этой непрерывной функции, чтобы получить 2.

Если вы нарисуете эту функцию, она выглядит как прямая f ( x ) = x — 2, но она имеет отверстие при x = 4, потому что исходная f все еще не определена (потому что она создает 0 в знаменателе). Эта цифра иллюстрирует это.

Если после того как вы учли верхнюю и нижнюю части дроби, термин в знаменателе не сократилось и значение, которое вы ищете не определен, f при этом значении x не существует (который вы можете написать как DNE ).

Например, эта f действует как показано:

(Х — 7) сверху и снизу сократятся. Поэтому, если вас попросят найти функцию, когда x подходит 7, вы можете подключить 7 в отмененную версию и получить 11/8. Но если вы пытаетесь найти

лимит DNE, потому что вы получите 0 в знаменателе. Следовательно, эта f имеет предельность где угодно, кроме как x приближается к -1.

Рационализация числителя

Третий метод требует, чтобы вы рационализировали числитель. Функции, требующие этого метода, имеют квадратный корень в числителе и полиномиальное выражение в знаменателе. Например, скажем, вас попросят вычислить предел этой функции по мере приближения x к 13:

Забивание номеров не получается, когда вы получаете 0 в знаменателе дроби. Факторинг терпит неудачу, потому что уравнение не имеет полиномиального фактора. В этой ситуации, если вы умножаете числитель и знаменатель на сопряжение числителя, термин в знаменателе, который был проблемой, отменяется, и вы сможете вычислить пределы:

Умножьте верхнюю и нижнюю части дроби конъюгатом.

Конъюгатом числителя является

Умножая, вы получаете эту настройку:

ИЗОБРАЖИТЕ числитель, чтобы получить

который упрощается до x — 13 (средние два члена отменяют, и вы объединяете как условия из FOIL).

Отменить факторы.

Отмена дает вам следующее выражение:

Условия ( x — 13) отменяются, оставляя вас с таким результатом:

Вычислите пределы.

Когда вы вставляете 13 в функцию, вы получаете 1/6, что является пределом.

Самый низкий общий знаменатель

Когда вам дается сложная рациональная f, вы используете четвертую и окончательную алгебраическую методику определения пределов. Техника подключения не работает, потому что вы получаете 0 в одном из знаменателей. Функция не факторизуема, и у вас нет квадратных корней для рационализации. Поэтому вы можете перейти к последней технике. С помощью этого метода вы комбинируете функции, найдя наименьший общий знаменатель (LCD). Термины отменяются, и в этот момент вы можете найти предельность.

Например, выполните следующие действия, чтобы найти ограничение:

Найдите ЖК-дисплей фракций сверху.

Распределите числители сверху.

Добавьте или вычтите числители, а затем отмените условия.

Вычитание числителей дает вам

который затем упрощает

Используйте правила для фракций для дальнейшего упрощения.

Замените предельное значение на эту функцию и упростите.

Для нахождения предела необходимо, когда x приближается к 0, поэтому здесь будет равен -1/36.

​Вот и все методы с подробным описанием — надеюсь, теперь вы поняли, как решать пределы.

Видео

Этот видеоурок поможет вам лучше разобраться в материале, изложенном в статье и запомнить его.