Как составить общее уравнение динамики

iSopromat.ru

Рассмотрим общее уравнение динамики механической системы, которое также называется принципом Даламбера-Лагранжа:

Объединяя этот принцип с принципом возможных перемещений для систем с идеальными связями получаем уравнение:

которое называют общим уравнением динамики (или принципом Даламбера-Лагранжа).

При движении механической системы с идеальными связями в каждый момент времени сумма элементарных работ всех приложенных активных сил и сил инерции на любом возможном перемещении системы будет равна нолю.

Поскольку в уравнении присутствуют силы инерции, а следовательно и ускорения, то эти уравнения представляют собой дифференциальные уравнения движения механической системы с идеальными связями.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Общее уравнение динамики. Пример решения задачи

Условие задачи

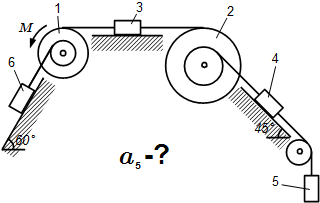
Механическая система состоит из однородных ступенчатых шкивов 1 и 2, обмотанных нитями, грузов 3-6, прикрепленных к этим нитям, и невесомого блока. Система движется в вертикальной плоскости под действием сил тяжести и пары сил с моментом M = 10 Н·м , приложенной к шкиву 1. Радиусы ступеней шкива 1 равны: R ₁ = 0,2 м , r ₁ = 0,1 м , а шкива 2 – R ₂ = 0,3 м , r ₂ = 0,15 м ; их радиусы инерции относительно осей вращения равны соответственно ρ ₁ = 0,1 м и ρ ₂ = 0,2 м .

Пренебрегая трением, определить ускорение груза 5. Веса шкивов и грузов заданы: P ₁ = 40 Н , P ₂ = 0 , P ₃ = 0 , P ₄ = 20 Н , P ₅ = 30 Н , P ₆ = 10 Н . Грузы, веса которых равны нулю, на чертеже не изображать.

Указание. При решении задачи использовать общее уравнение динамики (принцип Даламбера – Лагранжа).

Решение задачи

Дано: R ₁ = 0,2 м , r ₁ = 0,1 м , R ₂ = 0,3 м , r ₂ = 0,15 м , ρ ₁ = 0,1 м , ρ ₂ = 0,2 м . P ₁ = 40 Н , P ₂ = 0 , P ₃ = 0 , P ₄ = 20 Н , P ₅ = 30 Н , P ₆ = 10 Н , M = 10 Н·м .

Установление кинематических соотношений

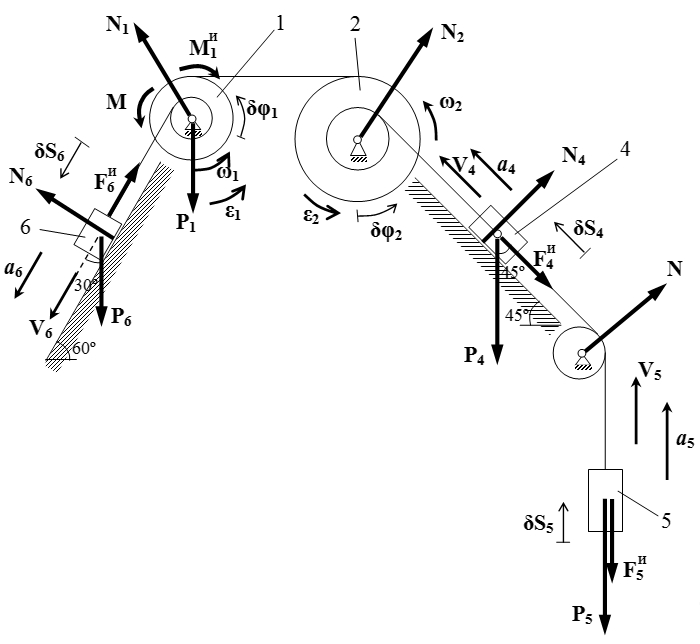
Установим кинематические соотношения. Пусть V ₄ , V ₅ , V ₆ , a ₄ , a ₅ , a ₆ , δS ₄ , δS ₅ , δS ₆ – скорости, ускорения и малые перемещения грузов 4,5 и 6. Пусть ω ₁ , ω ₂ , ε ₁ , ε ₂ , δφ ₁ , δφ ₂ – угловые скорости, угловые ускорения и малые углы поворота шкивов 1 и 2.

Скорость движения нити между телами 2, 4 и 5:
. Отсюда .
Скорость движения нити между шкивами 1 и 2:
. Отсюда
.
Скорость движения нити между телами 1 и 6:
.

Итак, мы нашли связь между скоростями тел.
;
;
.

Поскольку ускорения – это производные скоростей по времени, ,
то дифференцируя по времени предыдущие формулы, находим связь между ускорениями:
;
;
.

Поскольку скорости – это производные от перемещений по времени, то такая же связь есть между бесконечно малыми перемещениями.
;
;
.

Активные внешние силы

Рассмотрим внешние силы, действующие на систему.
Это силы тяжести тел P ₁ = 40 Н , P ₄ = 20 Н , P ₅ = 30 Н и P ₆ = 10 Н , направленные вниз;
заданная пара сил с моментом M = 10 Н·м ;
силы давления осей N ₁ , N ₂ и N шкивов 1, 2 и невесомого блока;
силы реакции N ₄ и N ₆ , действующие на грузы со стороны поверхностей, перпендикулярные этим поверхностям.

Силы инерции

Мы будем решать эту задачу с помощью общего уравнения динамики, применяя принцип Даламбера — Лагранжа. Он заключается в том, что сначала мы вводим силы инерции. После введения сил инерции, задача динамики превращается в задачу статики. То есть нам нужно найти неизвестные силы инерции, чтобы система находилась в равновесии. Данную задачу статики мы решаем, применяя принцип Даламбера. То есть считаем, что система совершила малое перемещение. Тогда в равновесии, сумма работ всех сил, при таком перемещении, равна нулю.

Итак, на первом этапе мы вводим силы инерции. Для этого предполагаем, что система движется с некоторым, пока не определенным, ускорением. То есть шкивы 1 и 2 вращаются с угловыми ускорениями ε ₁ и ε ₂ , соответственно; грузы 4,5 и 6 совершают поступательное движение с ускорениями a ₄ , a ₅ и a ₆ , соответственно. Между этими ускорениями имеются связи, которые мы нашли ранее. То есть все эти ускорения можно выразить через одно ускорение a ₅ . Силы инерции определяются так, что они равны по модулю и противоположны по направлению тем силам (и моментам сил), которые, по законам динамики, создавали бы предполагаемые ускорения (при отсутствии других сил).

Определяем модули (абсолютные значения) сил и моментов инерции и выражаем их через a ₅ .
Пусть – массы тел;
– момент инерции шкива 1.
Момент сил инерции, действующий на шкив 1:
.
Силы инерции, действующие на грузы 4, 5 и 6:
;
;
.

Изображаем силы инерции на чертеже учитывая, что их направления противоположны ускорениям.

Применение общего уравнения динамики

Даем системе бесконечно малое перемещение. Пусть груз 5 переместился на малое расстояние δS ₅ . Тогда угол поворота δφ ₁ шкива 1 и перемещения δS ₄ и δS ₆ грузов 4 и 6 определяются с помощью установленных ранее кинематических соотношений. Поскольку нити нерастяжимые, то они не совершают работу при таком перемещении. Это означает, что система имеет идеальные связи. Поэтому мы можем применить общее уравнение динамики:
,
согласно которому сумма работ всех активных сил и сил инерции, при таком перемещении, равна нулю.

Определение суммы работ внешних активных сил и сил инерции

Работа, которую совершает сила при перемещении точки ее приложения на малое смещение равна скалярному произведению векторов , то есть произведению модулей векторов F и ds на косинус угла между ними.

Работа, произведенная моментом сил , вычисляется аналогично:
.

Определяем работы всех активных сил и сил инерции. Поскольку центры осей шкивов 1, 2 и невесомого блока не совершают перемещений, то силы P ₁ , N ₁ , N ₂ и N не совершают работу. Поскольку силы N ₄ и N ₆ перпендикулярны перемещениям грузов 4 и 6, то эти силы также не совершают работу.

Находим сумму работ остальных активных сил и сил инерции.

.
Подставляем выражения для сил инерции и применяем кинематические соотношения.

.
Сокращаем на δS ₅ и преобразовываем.

.
Подставляем численные значения.

;
;
м/с 2 .

Автор: Олег Одинцов . Опубликовано: 02-08-2015

Общее уравнение динамики

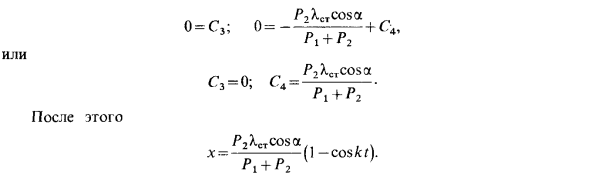
Общее уравнение динамики

• Соответствует балансу сил в каждой точке системы в соответствии с принципом Дарренва: механическая система, активная сила, объединенная сила реакции и сила инерции. Fk + Lk + Fk = 0, k = 1, 2, …, N, (23) Где Гк — активная сила. Rk — сила реакции связи; Фк — сила инерции точки. Умножение каждого из этих соотношений на возможное смещение точки 8rk на скаляр и суммирование всех точек в системе дает: ДFk ^ k + ДFk-8rk + ДФк • 8гк = 0. (24) Это общее уравнение динамики связанных систем. Обычно используется для систем с полной связью. * 5? * = 0- В этом случае (24) принимает одну из следующих форм (W) • «.» 0; (Ft-mta *) • 8rt = 0; D (^ — Людмила Фирмаль

В случае равновесия системы, если все силы инерции системы указывают на ноль, мы переходим к принципу статического возможного смещения без доказательства достаточности равновесия системы. Уравнениям общей динамики могут быть даны другие эквивалентные формы. Выявление скалярного произведения векторов можно выразить как: £ + ® „) Sy + (A, + Φ,.) 6 -.] — 0. Где xk, yk, zk — координаты k-й точки в системе. Учтите, что проекция сил инерции на оси координат за счет проекции ускорения на эти оси выражается следующей зависимостью: F * x =

тках = -тхх; Fku = -tkaku = -tkuk, F4; = -tkakg = -mkzk, общее уравнение для динамики дано в виде £ [(Ffc, -mjkxJk) 8xlk + (fi, -Wl | kA) 8 No. + (Fte-m) tfJk) 8zjk] = 0. (25 ‘).

В таком виде оно называется общим уравнением динамики в аналитическом виде. Общие уравнения для динамики систем, подверженных голономным и идеальным неразрывным связям, дают полную информацию о поведении таких систем. Это похоже на это. Вы можете получить полную систему дифференциальных уравнений о том, как равновесное состояние системы получается из принципа возможного смещения. Вывод этих уравнений требует использования обобщенных координат и обобщенных концепций сил. Предположим, у вас есть система, которая зависит от голономного, идеального, неизданного соединения.

Предположим, что положение в пространстве определяется обобщенными координатами qt, q2, …. q „, поскольку степень свободы равна n. Радиус-вектор каждой точки системы в общем случае нестационарных соотношений равен Обобщенные координаты и время, т. Е. ^ = M * (? 1, qz, nn, 0. (26) Потому что время считается неизменным. После подстановки (26) в общее динамическое уравнение (25) и изменения порядка сумм k и i получается следующее. к. (27) Используйте активную силу O, обобщенную силу O и силу инерции 21F ‘. (28) 4 = 1 * ‘? * = 1 001 Из (27) получите общее динамическое уравнение в следующем формате: Z (e (+ e> φ,) 8 ?. = ° — (29) Обобщенные координаты системы независимы. Эти изменения координат не только независимы, но и необязательны.

Предполагая, что только одна из обобщенных вариаций координат не равна нулю, а все остальные равны нулю, (29) дает следующую условную систему: 0 (+0! Φ) = 0, r = 1, 2, … и т. Д. (30) Условие (30) называется принципом Даламбера системы и выражается обобщенной силой. Условие уравнения для системы b следует (30), = 0, α = 1, 2, …, n, если сила инерции точки системы и, следовательно, обобщенная сила инерции, равна нулю. При использовании общих динамических уравнений необходимо уметь рассчитывать основную работу сил инерции системы при возможных смещениях. Для этого используется формула, соответствующая полученной работе начальной школы Для нормальной мощности.

• Рассмотрим приложение к силе инерции твердого тела для определенного движения. Поступательное движение. В этом случае тело имеет три степени свободы и принудительно соединено, поэтому может выполняться только поступательное движение. Движение тела, которое обеспечивает связь, также является поступательным движением. Инерционная сила при переносе уменьшается до результирующего Ф * = -Мас = -Ма. Для суммы основной работы силы инерции на возможность поступательного движения тела, ггйгй = = Φ * 8 8s = * * -8r = -L / d-8g, Где 8gs = 8g — возможное смещение центра тяжести и любой точки тела, потому что переводимое смещение одинаково во всех точках тела. Ускорение такое же, то есть как есть. Когда тело вращается вокруг фиксированной оси. Тело в этом случае имеет одну степень свободы.

Он может вращаться вокруг неподвижной оси Oz. Возможные перемещения, которые возможны благодаря наложенному соединению, такие же, как и вращение тела на базовый угол 8 (когда центр тяжести выбран в качестве центра торможения). Сумма основных сил инерции возможных инерционных перемещений на плоскости является основной работой главного вектора сил инерции = -массовая работа возможного движения центра масс и основной относительно оси Cz через центр масс Основной момент инерции общего вращательного движения сводится к работе элемента.

Следовательно, в этом случае ось ротора будет оставаться направленной на одну и ту же звезду и для наблюдателя, находящегося на Земле, она будет следовать за звездой в ее суточном движении. Людмила Фирмаль

В этом случае ненулевую базовую работу можно выполнить, только проецируя главный момент инерции на ось Cz, т.е. L $, = -JCze. Так что в рассматриваемом случае, ZФ * ’8г * = Ф-5гс + 1, . 8 , При повороте на базовый угол 8 ; z2 = 2Zcos «p. Изменяя эти зависимости, есть: 8.V] = Zcos ; Sz2 = -Zsin ; 8z2 = -2Zsin , оно становится следующим. — (Z1 + Zsinq>) «e2Z cosip-Z’sinip -cZsinipcosip -gsin 3-PTg -Qtg = официальный 1 приложение Система, предполагая, что координата FL-z постоянна, нам нужно вычислить инерцию смещения точки_ при изменении координаты x.

Поскольку мы дали 6x возможных движений в направлении увеличения координаты x, уравнение (b) 0! = O, сила тяжести Pt, P2 перпендикулярна возможному движению, сила упругости (одна добавляется к нагрузке, другая изначально равна, но направление противоположно), к призме точки крепления пружины ) В сумме приведем базовую работу, равную нулю с константой s. Для каждой обобщенной силы инерции -F18l-Ф2.8й. P, x + P2 (от cosa + x) Q \ * ‘= — = — (Ф 、 + Ф2 、) = —————!

= 8 раз Призма инерции Доска У нас есть @ P2sina83 — F6s Суммированная река Сена По возрастающей координате z всегда вычисляется по формуле.

Если s рассчитывается из положения статического равновесия нагрузки B, поскольку сила упругости F = cX = c (XCI + 3), HS — статическое растяжение пружины под действием силы тяжести. Равновесие. В положении Статика удовлетворяет условию Равновесие. Обобщенные Инерция у нас есть интеграция (A) Получите следующее Константа С, Synaf + cj, условия Со второй интеграцией x = -L ^^ lcoskt + Cjt + Cf — (S-h-xcosa), г Где Ф2 — проекция инерции нагрузки B на ось.

Подставьте полученное значение обобщенной системы нагнетания для дифференциального уравнения. Исключите следующее выражение для s из второго выражения: P2 [P | + P2 (1-интеграция (r), получить s

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института