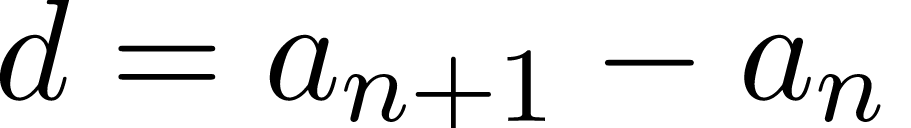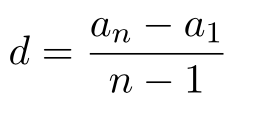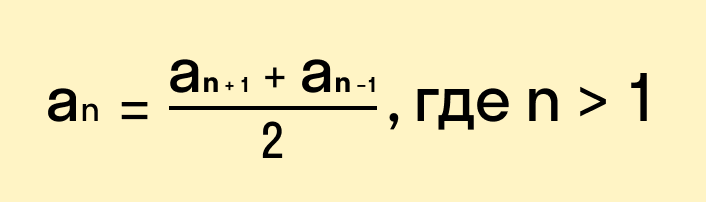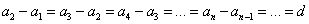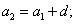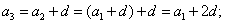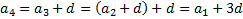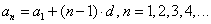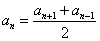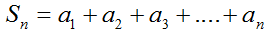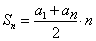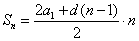Как составить уравнение арифметической прогрессии

Арифметическая прогрессия

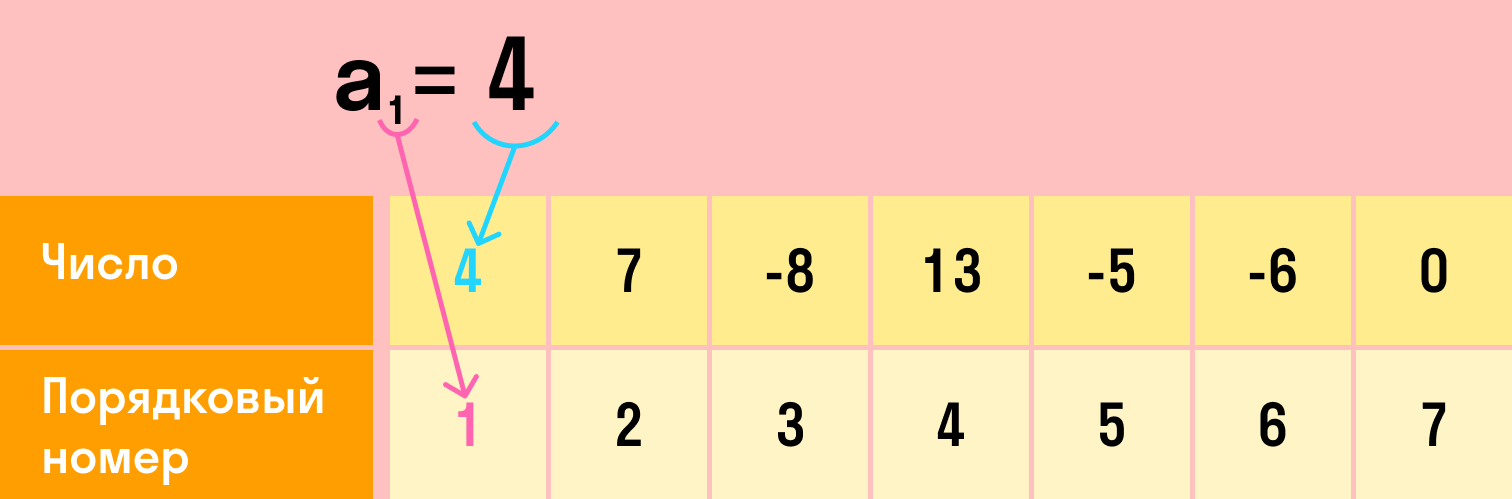
Арифметическая прогрессия — это числовая последовательность a1, a2, . , an, . , для которой для каждого натурального n выполняется равенство:

где d – это разность арифметической прогрессии.

Пример: последовательность чисел 3, 7, 11, 15, 19, . является арифметической прогрессией с разностью d = 4.

Арифметическая прогрессия бывает трех видов:

  1. Возрастающая — арифметическая прогрессия, у которой разность является положительной Пример: последовательность чисел 2, 5, 8, 11, 14, . является возрастающей арифметической прогрессией, так как ее разность d = 3.
  2. Убывающая— арифметическая прогрессия, у которой разность является отрицательной Пример: последовательность чисел 100, 98, 96, 94, 92, . является убывающей арифметической прогрессией, так как ее разность d = –2.
  3. Стационарная— арифметическая прогрессия, у которой разность равно нулю Пример: последовательность чисел 23, 23, 23, 23, 23, . является стационарной арифметической прогрессией, так как ее разность d = 0.

Основные формулы арифметической прогрессии

Члены арифметической прогрессии

Общая формула для вычисления n-ого члена арифметической прогрессии по первому члену и разности:

Следующий член арифметической прогрессии можно найти по предыдущему члену и разности:

Предыдущий член арифметической прогрессии можно найти по следующему члену и разности:

Также член арифметической прогрессии можно найти, если известны следующий и предыдущий члены:

Сумма арифметической прогрессии

Сумма первых n членов арифметической прогрессии равна

Также сумму можно вычислить, используя другую формулу:

Решение задач на арифметическую прогрессию

Рассмотрим несколько типичных задач, посвященных арифметической прогрессии.

Доказать, что последовательность, заданная формулой an = 5 + 4n, является арифметической.

Чтобы доказать, что последовательность является арифметической, достаточно получить следующий член этой последовательности и найти разность.

an+1 = 5 + 4(n + 1) = 5 + 4n + 4 = 9 + 4n

d = an+1 — an = 9 + 4n — (5 + 4n) = 9 + 4n — 5 — 4n = 4

Поскольку разность является числом, значит она будет одинакова для всех членов данной последовательности. Поэтому последовательность является арифметической прогрессией.

Найти 20 член арифметической прогрессии и сумму первых десяти, если a1 = -18 и d = 5

a20 = a1 + d ⋅ 19 = –18 + 5 ⋅ 19 = 77

S10 = (2 ⋅ (–18) + 5 ⋅ 9) ⋅ 10 / 2 = 45

Число 85 является членом арифметической прогрессии 8, 15, 22, 29, . . Найти номер этого члена.

Пусть n — номер, который нужно найти.

Применив формулу для вычисления n-ого члена арифметической прогрессии, можно получить n

В арифметической прогрессии a8 = 22 и a14 = 34. Найти формулу для n-ого члена.

Применив формулу для вычисления n-ого члена арифметической прогрессии по первому члену и разности находим:

Подставив в эти выражения a8 и a14 получаем систему уравнений:

Вычитая из первого уравнения второе, можно вычислить d:

Подставляем d в первое уравнение для получения a1:

Таким образом, формула для n-ого члена арифметической прогрессии выглядит так:

an = 8 + 2 ⋅ (n — 1) = 8 + 2n — 2 = 6 + 2n

Найти количество членов арифметической прогрессии 1, 3, 5, 7, . , если их сумма равна 81.

Из заданной арифметической прогрессии получаем a1 и d:

И подставляем известные данные в формулу суммы:

Арифметическая прогрессия: свойства и формулы

О чем эта статья:

Определение числовой последовательности

Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.

Последовательности можно задавать разными способами:

    Словесно — когда правило последовательности объясняется словами:

«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23. »

Аналитически — когда указана формула ее n-го члена: yn = f(n).

Последовательность yn = C называют постоянной или стационарной.

Рекуррентно — когда указывается правило, которое помогает вычислить n-й член последовательности, если известны её предыдущие члены.

Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.

Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.

  • Графически — когда график последовательности состоит из точек с абсциссами
    1, 2, 3, 4.

    • Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.

    Свойства числовых последовательностей:

      Последовательность n> называют возрастающей, если каждый ее член кроме первого больше предыдущего:

    Возрастающие и убывающие последовательности называют монотонными последовательностями.

  • Последовательность можно назвать периодической, если существует такое натуральное число T, что начиная с некоторого N, выполняется равенство: yn = yn+T. Число T — длина периода.

    • Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.

    Пример числовой последовательности выглядит так:

    В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.

    N-ный член алгебраической последовательности — это число с порядковым номером n.

    Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2. a10. an.

    N-ый член последовательности можно задать формулой. Например:

    • Формула an = 3n − 5 задает последовательность: −2, 1, 4, 7, 10…
    • Формула an = 1 : (n + 2) задает последовательность: 1/3, 1/4, 1/5, 1/6.

    Определение арифметической прогрессии

    Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.

    Рассмотрим основные определения и как найти арифметическую прогрессию.

    Арифметическая прогрессия — это числовая последовательность a1, a2. an. для которой для каждого натурального n выполняется равенство:

    an+1= an + d, где d — это разность арифметической прогрессии.

    Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

    Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

    Если известны первый член a1 и n-ый член прогрессии, разность можно найти так:

    Арифметическая прогрессия бывает трех видов:

      Возрастающая — арифметическая прогрессия, у которой положительная разность, то есть d > 0.

    Пример: последовательность чисел 11, 14, 17, 20, 23. — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

    Убывающая — арифметическая прогрессия, у которой отрицательная разность, то есть d

    Свойство арифметической прогрессии

    Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

    Формула n-го члена арифметической прогрессии

    Из определения арифметической прогрессии следует, что равенство истинно:

    Значит,

    Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

    Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

    Формулу an = a1 + d * (n — 1) называют формулой n-го члена арифметической прогрессии.

    Формулы арифметической прогрессии

    В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

    1. Рекуррентной формулой:
    2. Формулой n-го члена: an = a1+ d · (n — 1).
    3. Формулой вида an = kn + b, где k и b — числа, n — число членов последовательности.

    Сумма первых n членов арифметической прогрессии (аn) обозначается Sn:

    Формулы нахождения суммы n членов арифметической прогрессии:


    Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

    Рассмотрим пример арифметической прогрессии.

    Дано: арифметическая прогрессия (an), где a1 = 0 и d = 2.

    Найти: первые пять членов прогрессии и десятый член прогрессии.

    Решение арифметической прогрессии:

      Чтобы найти последующий член прогрессии, нужно к предыдущему прибавить разность:

    Используем общую формулу an = a1 + d * (n — 1).

    По условиям задачи n = 10, подставляем в формулу:

    a10 = a1 + 2 * (10 — 1) = 0 + 2⋅9 = 18.

    Геометрическая прогрессия

    Геометрическая прогрессия — это последовательность (bn), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

    Если последовательность (bn) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

    bn+1 = bn * q, где q — знаменатель геометрической прогрессии

    Если в геометрической прогрессии (bn) известен первый член b1 и знаменатель q, то можно найти любой член прогрессии:

    Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

    bn = b1 * q n−1 , где n — порядковый номер члена прогрессии, b1 — первый член прогрессии, q — знаменатель.

    Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

    Пример 2. 3, -3, 3, -3,… — геометрическая прогрессия b = 3, q = -1.

    Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.

    Арифметическая прогрессия

    п.1. Понятие арифметической прогрессии

    Например:
    1. Последовательность 2, 5, 8, 11, 14, . является арифметической прогрессией с разностью d = 3.

    2. Последовательность 12, 9, 6, 3, 0, –3, –6, . является арифметической прогрессией с разностью d = –3.

    п.2. Формула n-го члена арифметической прогрессии

    По определению арифметической прогрессии мы получаем рекуррентную формулу для n-го члена: an = an-1 + d. Из неё можно вывести аналитическую формулу:

    Например:
    Найдём a7, если известно, что a1 = 5, d = 3.
    По формуле n-го члена получаем: a7 = a1 + 6d = 5 + 6 · 3 = 23

    п.3. Свойства арифметической прогрессии

    Свойство 1. Линейность

    Арифметическая прогрессия является линейной функцией f(n) = kn + b:

    с угловым коэффициентом k = d и свободным членом b = a1 – d.

    Свойство 2. Признак арифметической прогрессии

    Для того чтобы числовая последовательность была арифметической прогрессией необходимо и достаточно, чтобы каждый её член, начиная со второго, был средним арифметическим предыдущего и последующего членов: $$ \mathrm < \left\— \text<арифметическая прогрессия>\ \Leftrightarrow\ a_n=\frac+a_><2>,\ \ n\in\mathbb,\ \ n \geq 2 > $$ Следствие: каждый член прогрессии является средним арифметическим двух равноудалённых от него членов: $$ \mathrm< a_n=\frac+a_><2>,\ \ n\in\mathbb,\ \ n\in\mathbb,\ \ n \geq k+1 > $$

    Например:
    Найдём a9, если известно, что a7 = 10, a11 = 15
    По следствию из признака арифметической прогрессии: \(\mathrm><2>=\frac<10+15><2>=12,5>\)

    Свойство 3. Равенство сумм индексов

    Если n> – арифметическая прогрессия, то из равенства сумм индексов следует равенство сумм членов: $$ \mathrm < m+k=p+q \Rightarrow a_m+a_k=a_p+a_q >$$ Следствие: сумма членов, равноудалённых от концов прогрессии, является постоянной величиной: $$ \mathrm< a_1 + a_n=a_2+a_=a_3+a_=. > $$

    Например:
    Найдём a6, если известно, что a2 = 5, a4 = 10, a8 = 20
    По равенству сумм индексов a2 + a8 = a4 + a6
    Откуда a6 = a2 + a8 – a4 = 5 + 20 – 10 = 15

    п.4. Сумма первых n членов арифметической прогрессии

    Например:
    Найдём сумму первых 100 натуральных чисел: 1 + 2 +. + 100
    В этом случае a1 = 1, a100 = 100, n = 100
    \(\mathrm< S_<100>=\frac<1+100><2>\cdot 100=5050>\)

    п.5. Примеры

    Пример 1. Найдите первый член и разность арифметической прогрессии, если:
    а) a7 = 10, a15 = 42
    Найдем разность данных членов: a15 – a7 = (a1 + 14d) – (a1 + 6d) = 8d
    Получаем разность прогрессии: 42 – 10 = 8d ⇒ d = 32 : 8 = 4
    7-й член: a7 = a1 + 6d = a1 + 6 · 4 = 10 ⇒ a1 = 10 – 24 = –14
    Ответ: a1 = –14, d = 4

    б) a10 = 95, S10 = 500
    Сумма прогрессии: \(\mathrm=\frac><2>\cdot 10\Rightarrow 500=(a_1+95)\cdot 5\Rightarrow a_1+95=100\Rightarrow a_1=5>\)
    10-й член: \(\mathrm=a_1+9d\Rightarrow95=5+9d\Rightarrow 9d=90\Rightarrow d=10>\)
    Ответ: a1 = 5, d = 10

    Пример 2. Найдите сумму первых 100 нечётных натуральных чисел.
    Чему равно последнее слагаемое этой суммы?
    Ищем сумму \(\mathrm<\underbrace<1+3+5+. >_<100\ \text<слагаемых>>>\)
    По условию a1 = 1, d = 2, n = 100. Получаем:
    \(\mathrm=\frac<2a_1+d(n-1)><2>n=\frac<2\cdot 1+2\cdot 99><2>\cdot 100=10000>\)
    Формула n-го члена данной прогрессии: \(\mathrm\)
    100-й член \(\mathrm=2\cdot 100-1=199>\)
    Ответ: S100 = 10000, a100 = 199

    Пример 3*. Сколько членов арифметической прогрессии 10, 16, 22, . находится между числами 110 и 345?
    По условию a1 = 10, d = 16 – 10 = 6
    Формула n-го члена данной прогрессии an = a1 + d(n – 1) = dn + (a1 – d) = 6n + 4
    Заданные числа могут быть членами данной прогрессии или находиться по «соседству» с ними. Подставим их в формулу для n-го члена: \begin \mathrm< 6k+4=110\Rightarrow 6k=106\Rightarrow k=17\frac23\Rightarrow 17\lt k\lt 18 >\\ \mathrm < 6m+4=345\Rightarrow 6m=341\Rightarrow m=56\frac56\Rightarrow 56\lt m\lt 57 >\end Ближайший сосед справа к 100 – это a18 = 6 · 18 + 4 = 112, k = 18
    Ближайший сосед слева к 345 – это a56 = 6 · 56 + 4 = 340, m = 56

    Количество членов прогрессии в заданном интервале:

    n = m – k + 1 = 56 – 18 + 1 = 39

    Пример 4. Одиннадцатый член арифметической прогрессии равен 7.
    Найдите сумму её первых 21 членов.
    По свойству суммы индексов: a11 + a11 = a1 + a21
    Откуда a1 + a21 = 2a11 = 14
    Искомая сумма: \(\mathrm=\frac><2>\cdot 21=\frac<14><2>\cdot 21=147>\)
    Ответ: 147

    Пример 5. Величины углов выпуклого пятиугольника образуют арифметическую прогрессию. Найдите третий член этой прогрессии.
    Сумма углов выпуклого пятиугольника S5 = 180° · (5 – 2) = 540°
    Если углы образуют арифметическую прогрессию, то: $$ \mathrm< S_5=\frac<2>\cdot 5=540^\circ\Rightarrow a_1+a_5=216^\circ > $$ По свойству суммы индексов: a3 + a3 = a1 + a5
    Откуда: \(\mathrm<2>=108^\circ>\)
    Ответ: 108°

    Пример 6. При каких значениях x числа x 2 – 11, 2x 2 + 29, x 4 – 139 в заданной последовательности являются членами арифметической прогрессии?
    Для последовательных членов получаем уравнение:

    a2 – a1 = a3 – a2
    (2x 2 + 29) – (x 2 – 11) = (x 4 – 139) – (2x 2 + 29)
    x 4 – 3x 2 – 208 = 0 ⇒ (x 2 + 13)(x 2 – 16) = 0 ⇒ x 2 = 16 ⇒ x = ±4

    Пример 7. Сумма первых трёх членов убывающей арифметической прогрессии равна 9, а сумма их квадратов равна 99. Найдите седьмой член прогрессии.
    По условию d 3a2 = 9 ⇒ a_2 = 3

    Тогда a1 = a2 – d = 3 – d, a3 = a2 + d = 3 + d. Подставляем во второе уравнение:

    (3 – d) 2 + 3 2 + (3 + d) 2 = 99
    9 – 6d + d 2 + 9 + 9 + 6d + d 2 = 99
    2d 2 = 72 ⇒ d 2 = 36 ⇒ d = ±6

    Выбираем отрицательное значение d = –6
    1-й член прогрессии: a1 = a2 – d = 3 + 6 = 9
    7-й член прогрессии: a7 = a1 + 6d = 9 + 6(–6) = –27
    Ответ: x = –27


    источники:

    http://skysmart.ru/articles/mathematic/arifmeticheskaya-progressiya

    http://reshator.com/sprav/algebra/9-klass/arifmeticheskaya-progressiya/

    © 2023 Русский язык. Привила написания. Наш первый проект тут и тут