Равнобедренный треугольник: свойства, признаки и формулы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение равнобедренного треугольника
Какой треугольник называется равнобедренным?
| Равнобедренным называется треугольник, у которого две стороны равны. |
Давайте посмотрим на такой треугольник:
На рисунке хорошо видно, что боковые стороны равны. Это равенство и делает треугольник равнобедренным.
А вот как называются стороны равнобедренного треугольника:
AB и BC — боковые стороны,
AC — основание треугольника.
Для понимания материала нам придется вспомнить, что такое биссектриса, медиана и высота, если вы вдруг забыли.
Биссектриса — луч, который исходит из вершины угла и делит этот угол на два равных угла.
Даже если вы не знаете определения, то про крысу, бегающую по углам и делящую их пополам, наверняка слышали. Она не даст вам забыть, что такое биссектриса. А если вам не очень приятны крысы, то вместо нее бегать может кто угодно. Биссектриса — это киса. Биссектриса — это лИса. Никаких правил для воображения нет. Все правила — для геометрии.
Обратите внимание на рисунок. В представленном равнобедренном треугольнике биссектрисой будет отрезок BH.
Медиана — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
Для медианы не придумали веселого правила, как с биссектрисой, но можно его придумать. Например, буддийская запоминалка: «Медиана — это Лама, бредущий из вершины треугольника к середине его основания и обратно».
В данном треугольнике медианой является отрезок BH.
Высота треугольника — перпендикуляр, опущенный из вершины треугольника на противоположную сторону или на прямую, содержащую сторону треугольника.
Высотой в представленном равнобедренном треугольнике является отрезок BH.
Признаки равнобедренного треугольника
Вот несколько нехитрых правил, по которым легко определить, что перед вами не что иное, как его величество равнобедренный треугольник.
- Если у треугольника два угла равны, то этот треугольник — равнобедренный.
- Если высота треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если высота треугольника совпадает с его биссектрисой, проведенной из того же угла, то такой треугольник — равнобедренный.
- Если биссектриса треугольника совпадает с его медианой, проведенной из того же угла, то такой треугольник снова равнобедренный!
Свойства равнобедренного треугольника
Чтобы понять суть равнобедренного треугольника, нужно думать как равнобедренный треугольник, стать равнобедренным треугольником — и выучить 4 теоремы о его свойствах.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Пусть AС — основание равнобедренного треугольника. Проведем биссектрису DK. Треугольник ADK равен треугольнику CDK по двум сторонам и углу между ними (AD = DC, DK — общая, а так как DK — биссектриса, то угол ADK равен углу CDK). Из равенства треугольников следует равенство всех соответствующих элементов, значит угол A равен углу C. Изи!
Теорема 2: В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Δ ABH = Δ CBH по двум сторонам и углу между ними (углы ABH и CBH равны, потому что BH биссектриса, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, AH = HC и BH — медиана.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит, они равны по 90 градусов и BH — высота.
Теорема 3: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Δ ABH = Δ CBH по трём сторонам (AH = CH равны, потому что BH медиана, AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, углы BHA и BHC равны, а ещё они смежные, т. е. в сумме дают 180 градусов. Значит они равны по 90 градусов и BH — высота.
Теорема 4: В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Δ ABH = Δ CBH по признаку прямоугольных треугольников, равенство гипотенуз и соответствующих катетов (AB = BC, потому что Δ ABC равнобедренный, BH — общая сторона).
Значит, во-первых, углы ABH и CBH равны и BH — биссектриса.
Во-вторых, AH = HC и BH — медиана.
Примеры решения задач
Нет ничего приятнее, чем поупражняться и поискать углы и стороны в равнобедренном треугольнике. Ну… почти ничего.
Задачка раз. Дан ΔABC с основанием AC: ∠C = 80°, AB = BC. Найдите ∠B.
Поскольку вы уже знакомы с различными теоремами, то для вас не секрет, что углы при основании в равнобедренном треугольнике равны, а треугольник ABC — равнобедренный, так как AB = BC.
Значит, ∠A = ∠C = 80°.
Не должно вас удивить и то, что сумма углов треугольника равна 180°.
∠B = 180° − 80° − 80° = 20°.
Задачка два. В треугольнике ABC провели высоту BH, угол CAB равен 50°, угол HBC равен 40°. Найдите сторону BC, если BA = 5 см.
Сумма углов треугольника равна 180°, а значит в Δ ABH мы можем узнать угол ABH, который будет равен 180° − 50° − 90° = 40°.
А ведь получается, что углы ABH и HBC оба равны по 40° и BH — биссектриса.
Ну и раз уж BH является и биссектрисой, и высотой, то Δ ABC — равнобедренный, а значит BC = BA = 5 см.
Изучать свойства и признаки равнобедренного треугольника лучше всего на курсах по математике с опытными преподавателями в Skysmart.
Равнобедренный треугольник. Онлайн калькулятор
С помощю этого онлайн калькулятора можно найти неизвестные элементы (стороны, углы) а также периметр, площадь, высоты равнобедренного треугольника. Теоретическую часть и численные примеры смотрите ниже.
| Открыть онлайн калькулятор |
Определение равнобедренного треугольника
Определение 1 (Евклид). Треугольник, в котором длины двух сторон равны между собой называется равнобедренным треугольником.
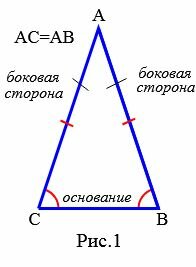
Равные стороны равнобедренного трекугольника называются боковыми сторонами. Третья сторона равнобедренного треугольника называется основанием треугольника (Рис.1).
Угол между боковыми сторонами равнобедненного треугольника (\( \small \angle A \) ) называется вершинным углом. Углы между основанием и боковыми сторонами (\( \small \angle B, \ \angle C \) ) называются углами при основании.
 |
Существует более общее определение равнобедненого треугольника:
Определение 2 (Современная трактовка). Треугольник, в котором длины хотя бы двух сторон равны между собой называется равнобедренным треугольником.
Из определения 2 следует, что равносторонний треугольник является частным случаем равнобедренного треугольника. Действительно, в качестве равных сторон можно взять любые две стороны равностороннего треугольника, а третья сторона будет основанием.
Теорема о равнобедренном треугольнике
Теорема 1. Углы, прилежащие к основанию равнобедренного треугольника равны.
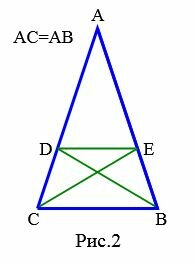 |
Доказательство (доказательство Прокла). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.2). Докажем, что \( \small \angle B= \angle C. \) Возьмем любую точку D на стороне AC и точку E на стороне AB так, чтобы AD=AE. Проведем отрезки DE, CE, BD. Треугольники ABD и ACE равны по двум сторонам и углу между ними: AE=AD, AC=AB, угол \( \small \angle A \) общий (см. статью на странице Треугольники. Признаки равенства треугольников). Отсюда следует:
| \( \small CE=BD,\) | (1) |
| \( \small \angle ACE=\angle ABD.\) | (2) |
Из \( \small AB=AC\) и \( \small AD=AE \) следует:
| \( \small CD=BE.\) | (3) |
Рассмотрим треугольники CBE и BCD. Они равны по трем сторонам: \( \small CE=BD,\) \( \small CD=BE ,\) сторона \( \small BC \) общая. Отсюда следует, что
| \( \small \angle ECB= \angle DBC. \) | (4) |
Из (2) и (4) следует, что \( \small \angle B= \angle C. \)
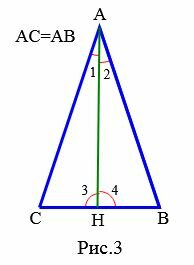 |
Доказательство (Вариант 2). Пусть задан равнобедренный треугольник ABC, где AB=AC (Рис.3). Проведем биссектрису \( \small AH \) треугольника. Тогда \( \small \angle CAH=\angle BAH. \) Докажем, что \( \small \angle B= \angle C. \) Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle CAH=\angle BAH. \) Отсюда следует: \( \small \angle B= \angle C. \)
Свойства равнобедренного треугольника
Теорема 2. В равнобедренном треугольнике биссектриса проведенная к основанию является медианой и высотой.
Доказательство. Рассмотрим равнобедренный треугольник ABC, где AB=AC, а AH− биссектриса треугольника (Рис.3). Треугольники AHB и AHC равны по двум сторонам и углу между ними: AC=AB, сторона \( \small AH \) общая, \( \small \angle 1=\angle 2. \) Тогда \( \small CH=HB, \) \( \small \angle 3=\angle 4. \) Равенство \( \small CH=HB \) означает, что \( \small AH \) является также медианой треугольника ABC. Углы \( \small \angle 3\) и \( \angle 4 \) смежные. Следовательно их сумма равна 180° и, поскольку эти углы равны, то каждый из этих углов равен 90°. Тогда \( \small AH \) является также высотой треугольника \( \small ABC. \) Поскольку высота \( \small AH \) перпендикулярна к \( \small BC \) и \( \small CH=HB, \) то \( \small AH \) является также серединным перпендикуляром к основанию равнобедренного треугольника.
Мы доказали, что биссектриса, медиана, высота и серединный перпендикуляр равнобедренного треугольника, проведенные к основанию совпадают.
Исходя из теоремы 2 можно сформулировать следующие теоремы, доказательство которых аналогично доказательству теоремы 2:
Теорема 3. В равнобедренном треугольнике медиана проведенная к основанию является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота проведенная к основанию является биссектрисой и медианой.
Признаки равнобедренного треугольника
Признак 1. Если в треугольнике две стороны равны, то треугольник является равнобедренным.
Признак 1 следует из определения 1.
Признак 2. Если в треугольнике два угла равны, то треугольник является равнобедренным.
Доказательство признака 2 смотрите в статье Соотношения между сторонами и углами треугольника (Следствие 2. Признак равнобедренного треугольника).
Признак 3. Если в треугольнике высота проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
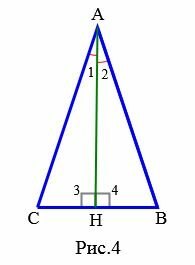
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и медианой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small CH=HB. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по двум сторонам и углу между ними (первый признак равенства треугольников): \( \small AH \) − общая сторона, \( \small CH=HB, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
Признак 4. Если в треугольнике высота проведенная к одной стороне совпадает с биссектрисой проведенной к этой же стороне, то треугольник является равнобедренным.
Доказательство. Пусть в треугольнике \( \small ABC \) \( \small AH \) является высотой и биссектрисой (Рис.4). Тогда \( \small \angle 3=\angle4=90°, \) \( \small \angle 1=\angle2. \) Треугольники \( \small AHC \) и \( \small AHB \) равны по стороне и прилежащим двум углам (второй признак равенства треугольников): \( \small AH \) − общая сторона, \( \small \angle 1=\angle 2, \) \( \small \angle 3=\angle4. \) Следовательно \( \small AB=AC. \)
  |
Признак 5. Если в треугольнике биссектриса проведенная к одной стороне совпадает с медианой проведенной к этой же стороне, то треугольник является равнобедренным.
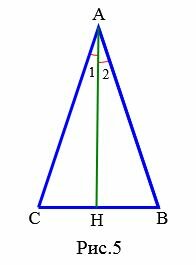
Доказательство (Вариант 1). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой (Рис.5). Тогда
| \( \small \angle 1=\angle2, \) \( \small CH=HB. \) | (5) |
Применим теорему синусов для треугольника \( \small AHC \):
| \( \small \frac <\large CH><\large \sin \angle 1>= \frac <\large AH><\large \sin \angle C>. \) | (6) |
Применим теорему синусов для треугольника \( \small AHB \):
| \( \small \frac <\large HB><\large \sin \angle 2>= \frac <\large AH><\large \sin \angle B>. \) | (7) |
тогда, из (5), (6), (7) получим:
| \( \small \frac <\large AH><\large \sin \angle C>= \frac <\large AH><\large \sin \angle B>. \) | (8) |
Следовательно \( \small \sin \angle C= \sin \angle B. \) Поскольку сумма всех углов треугольника равна 180°, то нам интересует синус углов от 0 до 180°. Учитывая это получим, что синусы углов равны в двух случаях: 1) \( \small \angle C= \angle B, \) 2) \( \small \angle C= 180° — \angle B. \) Поскольку сумма двух углов треугольника меньше 180°: \( \small \angle C + \angle B Доказательство (Вариант 2). Пусть в треугольнике \( \small ABC \) \( \small AH \) является биссектрисой и медианой, т.е. \( \small \angle 1=\angle 2, \) \( \small CH=HB \) (Рис.6). На луче \( \small AH \) отложим отрезок \( \small HD \) так, чтобы \( \small AH=HD. \) Соединим точки \( \small C \) и \( \small D. \)
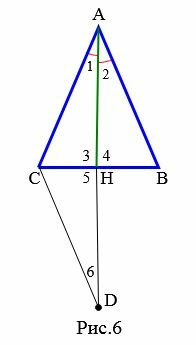 |
Треугольники \( \small AHB \) и \( \small DHC \) равны по двум сторонам и углу между ними (первый признак равенства треугольников). Действительно: \( \small AH=HD, \) \( \small CH=HB, \) \( \small \angle 4=\angle 5 \) (углы 4 и 5 вертикальные). Тогда \( \small AB=CD, \) \( \small \angle 6=\angle 2. \) Отсюда \( \small \angle 6=\angle 1. \) Получили, что треугольник \( \small CAD \) равнобедренный (признак 2). Тогда \( \small AC=CD. \) Но \( \small AB=CD \) и, следовательно \( \small AB=AC. \) Получили, что треугольник \( \small ABC \) равнобедренный.
1. Признак равенства равнобедренных треугольников по основанию и боковой стороне
Если основание и боковая сторона одного равнобедренного треугольника соответственно равны основанию и боковой стороне другого равнобедненного треугольника, то эти треугольники равны.
Действительно. Поскольку треугольник равнобедренный, то боковые стороны равны. То есть три стороны одного равнобедренного треугольника соответственно равны трем сторонам другого равнобедненного треугольника. А по третьему признаку равенства треугольников, эти треугольники равны.
2. Признак равенства равнобедренных треугольников по боковой стороне и углу при вершине
Если боковая сторона и угол при вершине одного равнобедренного треугольники соответственно равны боковой стороне и углу при вершине другого равнобедренного треугольника, то такие треугольники равны.
Действительно. Так как боковые стороны равнобедненного треугольника равны, то имеем: две стороны и угол между ними одного треугольника соотвественно равны двум сторонам и углу между ними другого треугольника. Тогда по первому признаку равенства треугольников, эти реугольники равны.
3. Признак равенства равнобедренных треугольников по основанию и углу при основании
Если основание и угол при основании равнобедренного треугольника соответственно равны основанию и углу при основании другого равнобедренного треугольника, то такие треугольники равны.
Доказательство. В равнобедренном треугольнике углы при основании равны. тогда имеем: основание и две углы одного равнобедненного треугольника равны основанию и двум углам другого равнобедненного треугольника. Тогда эти треугольники равны по второму признаку равенства треугольников.
Задачи и решения
Задача 1. Известны основание \( \small a=5 \) и высота \( \small h=6 \) равнобедренного треугольника. Найти углы, боковые стороны, периметр, площадь.
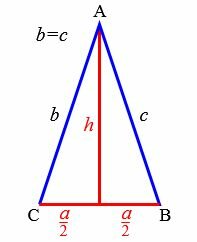 |
Решение. Найдем боковые стороны \( \small b \) и \( \small c \) равнобедренного треугольника. Воспользуемся теоремой Пифагора:
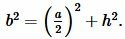 |
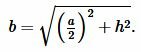 | (9) |
Подставляя значения \( \small a \) и \( \small h \) в (9), получим:
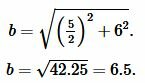 |
Боковая сторона \( \small c \) равнобедренного треугольника равна:
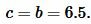 |
Найдем периметр треугольника. Периметр треугольника равен сумме длин его сторон:
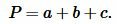 | (10) |
Подставляя значения \( \small a=5, \) \( \small b=6.5 \) и \( \small c=6.5 \) в (10), получим:
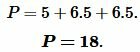 |
Найдем угол \( \small B \) равнобедренного треугольника:
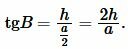 | (11) |
Подставляя значения \( \small a=5, \) \( \small h=6 \) в (11), получим:
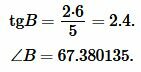 |
Тогда угол \( \small C \) равнобедренного треугольника равен:
 |
Поскольку сумма всех углов треугольника равна 180°, то имеем:
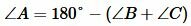 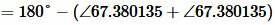 , , |
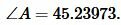 |
Площадь треугольника можно вычислить из формулы:
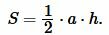 | (12) |
Подставляя значения \( \small a=5, \) \( \small h=6 \) в (12), получим:
Составить уравнение катетов прямоугольного равнобедренного треугольника
УСЛОВИЕ:
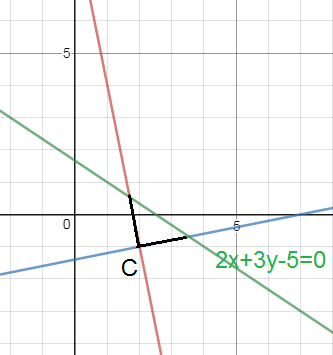
Помогите решить, пожалуйста. Составить уравнения катетов прямоугольного треугольника, зная уравнение гипотенузы 2х+3у-5=0 и вершину прямого угла С(2;-1).
РЕШЕНИЕ ОТ sova ✪ ЛУЧШЕЕ РЕШЕНИЕ
Так и есть по ответам, треугольник прямоугольный равнобедренный.
Угловой коэффициент гипотенузы
k_(гипотенузы)=-2/3
Пусть угловой коэффициент одного катета
k_(1)
Формула тангенса разности двух углов
tg( α – β ) =(tg α -tg β )/(1+tg α *tg β )
((-2/3) -k_(1) )/(1+(-2/3) *k_(1) )=1
находим k_(1) и уравнение прямой первого катета, подставив координаты точки С в уравнение
y=k_(1)x+b
Так как катеты взаимно перпендикулярны, то угловой коэффициент второй прямой k_(2)=-1/k_(1)
Добавил vk492871866 , просмотры: ☺ 449 ⌚ 2019-04-19 15:17:02. математика 1k класс
Решения пользователей
Написать комментарий
Делим обе части равенства на π
и умножаем на 4
+pi k, k in Z
Можно правую часть записать в виде двух ответов:
x=1+8n in Z : это . [b] -15; -7; 1; 9; 17; ..[/b].
x=3+ 8n, n in Z : это[b] -13; -5; 3; 11; . [/b]
[b]x=-5 – наибольшее отрицательное [/b]
О т в е т. x=1+8n in Z или x=3+ 8n, n in Z
корни чередуются так:
. -15;-13;-7;-5; 1;3; 9;11; 17; 19; .
[b]x=-5 – наибольшее отрицательное [/b] (прикреплено изображение)
a=1 – старший коэффициент
b=1 – средний коэффициент
с=-2 – свободный член
4.
x^2=a-5
При a-5=0 ⇒ при а=5
уравнение имеет один корень х=0
5.
Δ Прямоугольный, так как верно равенство: b^2=a^2+c^2
5^2=3^2+4^2
25=9+16
Значит, ∠ B=90 градусов и ∠ А+ ∠ С=90 градусов.
∠ А- ∠ С=36 градусов.
∠ А+ ∠ С=90 градусов.
складываем оба равенства:
2* ∠ А=126 градусов.
По формулам приведения:
sin^2x+sinx-2=0
D=9
sinx=-2 или sinx=1
sinx=-2 уравнение не имеет корней, -1 ≤ sinx ≤ 1
sinx=1 ⇒ x=(π/2)+2πk, k ∈ Z или х=90 ° +360 ° *k, k ∈ Z
Найдем корни, принадлежащие указанному отрезку с помощью неравенства:
-286 ° ≤ 90 ° +360 ° *k ≤ 204 °
-286 °-90 ° ≤ 360 ° *k ≤ 204 ° -90 °
-376 ° ≤ 360 ° *k ≤ 114 °
Неравенство верно при k=[green]-1[/green] и k=[red]0[/red]
Значит, указанному отрезку принадлежат два корня:
x=90 ° +360 °* ([green]-1[/green])=-270 °
x=90 ° +360 °*[red]0[/red]=90 °
7. KT- средняя линия трапеции:
Cредняя линия трапеции делит высоту трапеции пополам ( см. рис)
Высоты треугольников АКО и СОК равны половине высоты трапеции
S_( Δ АКО)+S_( Δ COK)=44
S_( Δ АКО)+S_( Δ COK)=KO*(h/4) +OT*(h/4)=
О т в е т. [b]176[/b]
B=-2
[i]l[/i]=8 – количество ребер четырехугольной пирамиды
3.4 Прямая на плоскости
Для прямой на плоскости мы приведем несколько уравнений. В зависимости от задачи удобнее использовать то или иное уравнение и довольно часто требуется перейти от уравнения прямой в одной форме к уравнению, описывающему прямую в другой форме.
 
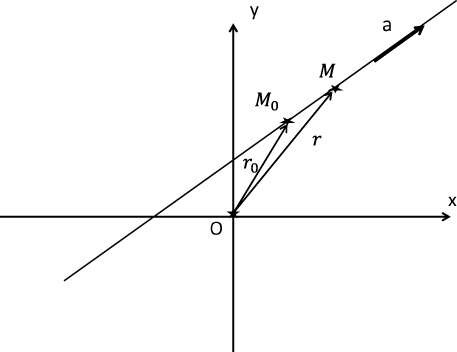
Рис 3: Прямая определяется точкой, через которую она проходит, и направляющим вектором.
 
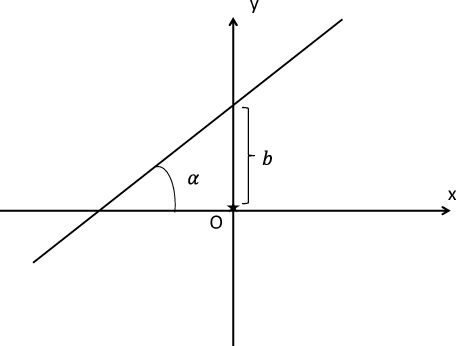
Рис 4: Прямая: фиксирован угловой коэффициент и отрезок, отсекаемый на оси $y$.
Проведем через точку $(-1,,1)$ прямую, параллельную прямой $2x+3y+7=0$. Эта прямая будет иметь уравнение $2x+3y+C=0$, где число $C$ подлежит определению (коэффициенты перед $x,,y$ определяют наклон прямой и если мы возьмем их, как в исходной прямой, получим параллельную прямую). Подставляя точку в искомую прямую, получим уравнение для $C$: $-2+3+C=0$, так что $C=-1$ и искомое уравнение прямой: $2x+3y-1=0$.
Пусть задано общее уравнение прямой на плоскости. Перепишите его в виде нормального уравнения прямой.
Решение типовых задач.
Написать уравнения прямой в общем виде и с угловым коэффициентом, если прямая проходит через точки $ extbf (2,3)$ и $ extbf (4,-6)$.
Для написания уравнения искомой прямой воспользуемся формулой (
ef
). Подставляя в нее вместо $(x_0,y_0)$ координаты точки $ extbf $, а вместо $(x_1,y_1)$ – координаты точки $ extbf $, получим [ frac =frac . ] или [ frac =frac . ] С помощью несложных элементарных преобразований (домножения на наименьший общий знаменатель, переноса в левую часть и приведения подобных слагаемых), получим уравнение в общем виде: [ 2y + 9x -24 = 0 ] Теперь приведем это уравнение к виду уравнения прямой с угловым коэффициентом: [ y = 12 – frac . ]
Две стороны параллелограмма заданы уравнениями $2x+5y+6=0$ и $x-3y=0$. Известны координаты одной из вершин параллелограмма – $ extbf (4;-1)$. Написать уравнения двух других сторон параллелограмма.
В параллелограмме противоположные стороны параллельны, значит исходная задача сводится к построению прямых, параллельных данным и проходящих через заданную точку. Построим прямую, параллельную прямой $2x+5y+6=0$. Ее уравнение будет иметь вид $2x+5y+C=0$. Значение $ extbf $ определим, подставив в это уравнение координаты точки $ extbf $: $2 cdot 4 + 5 cdot (-1) + C=0$. Следовательно, $ extbf $ и искомое уравнение стороны есть [ 2x+5y-3=0 ] Аналогичным образом, подставляя в уравнение $x-3y+C=0$ координаты точки $ extbf $: $4 -3 cdot (-1)+C=0$, получим уравнение другой стороны параллелограмма: [ x-3y-7=0. ]
Проверить, что прямые [ y = 3x-1, x+y-7=0, x-7y=7 ] служат сторонами равнобедренного треугольника.
Выяснить являются ли перпендикулярными прямые $3x-2y=0$ и $-4x-6y+3=0$.
Приведем уравнения к виду уравнений с угловыми коэффициентами: [ y = frac , y = -frac +frac ] Тогда угловой коэффициент первого уравнения $k_1=frac $, второго – $k_1=-frac $. Проверим условие ортогональности, согласно которому $k_1cdot k_2=-1$. В нашем случае имеем $k_1cdot k_2=frac cdot -frac = -1$ . Это означает, что заданные прямые перпендикулярны.
Найти расстояние от прямой $frac =frac $ до точки $P(2,-1)$.
Приводя исходное уравнение к общему виду, получим [ 3x+4y+1 =0. ] Расстояние от точки $P(2,-1)$ до прямой вычислим по формуле [ p=frac > = frac . ]
1. Составить уравнение прямой, проходящей через точку $ M(-2,1)$ и параллельной прямой [ frac =frac . ]
2. Составить уравнение прямой, проходящей через точку $M(-2,1)$ и перпендикулярной прямой [ frac =frac . ]
3. Найти угол между прямыми [ frac =frac , quad frac =frac . ]
4. Составить уравнение биссектрисы острого угла между прямыми $3y=4x$ и $5x+12y=6$.
5. Написать уравнение прямой, удаленной на 5 от прямой $12x+5y=39$.
6. Основания трапеции лежат на прямых [ 2x+sqrt y-24=0, quad 2x+sqrt y+6=0. ] Найти ее высоту.
7. Проверить, что прямые $2x+frac y-15=0$ и $frac x-5y+30=0$ касаются одной и той же окружности с центром в начале координат и вычислить ее радиус.
8. На расстоянии 5 от точки $M(4,3)$ провести прямую, отсекающую равные отрезки на осях координат.
9. На оси $y$ найти точку, равноудаленную от начала координат и от прямой $3x-4y=12=0$.
10. Через точку пересечения прямых $2x-y=2$ и $x+y=1$ провести прямую, параллельную прямой $y=3x-2$.
11. Составить уравнения катетов прямоугольного равнобедренного треугольника, зная уравнение гипотенузы $y=3x+5$ и вершину прямого угла $M(4,-1)$.
12. Вычислить координаты вершин ромба, если известны уравнения двух его сторон $2x-5y-1=0$ и $2x-5y-34=0$ и уравнение одной из диагоналей $x+3y-6=0$.
13. Найти уравнения сторон треугольника, зная одну из его вершин $A(3,4)$ и уравнения двух высот $7x-2y=1$ и $2x-7y=6$.
14. Через точку $M(0,1)$ провести прямую так, чтобы ее отрезок, заключенный между двумя данными прямыми $x-3y+10$ и $2x+y-8=0$, делился в этой точке пополам.
15. Составить уравнения сторон треугольника, зная одну из его вершин $A(-4,2)$ и уравнения двух медиан $3x-2y+2=0$ и $3x+5y-12=0$.
16. Даны две противоположные вершины квадрата $A(-5,2)$ и $C(3,-4)$. Составить уравнения его сторон.
Ответ или решение 1
1. Найдем расстояние l между точкой C(3; -1) и произвольной точкой M(x; y), лежащей на заданной прямой:
- 3x + 2y – 6 = 0;
- 2y = 6 – 3x;
- y = 3 – 1,5x;
- l^2 = (x – 3)^2 + (y + 1)^2;
- l^2 = (x – 3)^2 + (3 – 1,5x + 1)^2;
- l^2 = (x – 3)^2 + (4 – 1,5x)^2;
- l^2 = x^2 – 6x + 9 + 16 – 12x + 2,25x^2;
- l^2 = 3,25x^2 – 18x + 25;
- l^2 = 13/4 * x^2 – 18x + 25;
- l^2 = 13/4(x^2 – 72/13 * x + 100/13);
- l^2 = 13/4((x – 36/13)^2 – 1296/13 + 100/13);
- l^2 = 13/4((x – 36/13)^2 – 1296/13^2 + 1300/13^2);
- l^2 = 13/4((x – 36/13)^2 + 4/13^2);
- l^2 = 13/4(x – 36/13)^2 + 1/13.
2. Высота CH равнобедренного прямоугольного треугольника ABC (http://bit.ly/2MLdSeb), проведенная к гипотенузе AB, равна половине гипотенузы AB и наименьшему значению l:
3. А длина катетов AC и BC в √2 раз больше высоты CH:
отсюда получим уравнение для координат вершин A и B:
- l^2 = 2/13;
- 13/4(x – 36/13)^2 + 1/13 = 2/13;
- 13/4(x – 36/13)^2 = 1/13;
- (x – 36/13)^2 = 4/13^2;
- (x – 36/13)^2 = (2/13)^2;
- x – 36/13 = ±2/13;
- x = 36/13 ± 2/13;
- x = (36 ± 2)/13;
1) x = (36 – 2)/13 = 34/13;
y = 3 – 1,5x = 3 – 3/2 * 34/13 = 39/13 – 51/13 = -12/13;
2) x = (36 + 2)/13 = 38/13;
y = 3 – 1,5x = 3 – 3/2 * 38/13 = 39/13 – 57/13 = -18/13.
http://matworld.ru/geometry/ravnobedrennyj-treugolnik.php
http://4apple.org/sostavit-uravnenie-katetov-prjamougolnogo/