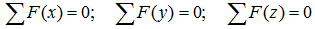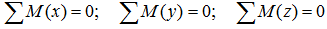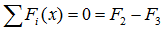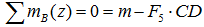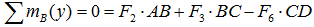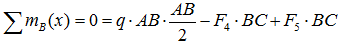iSopromat.ru
Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.
При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат
что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы
из условия отсутствия ее вращения относительно указанных осей.
Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.
Пример составления уравнений равновесия
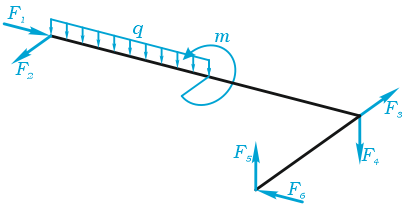
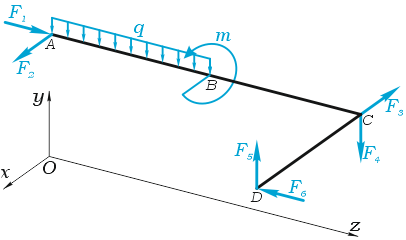
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F1-F6, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.
Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.
Суммы проекций сил
Сумма проекций всех сил на ось x (с учетом правила знаков для сил):
здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.
Суммы моментов
Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):
- в плоскости xOy:
- в плоскости xOz:
- в плоскости yOz:
Из полученных шести уравнений можно определить не более шести неизвестных усилий.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Методы определения реакций опор твердого тела
Как определить реакции опор твердого тела
Чтобы определить реакции опор твердого тела нужно выполнить следующие шаги.
- Вместо связей в опорах приложить силы реакций.
- Если есть распределенная нагрузка, то заменить ее равнодействующей силой. Ее величина равна площади эпюры нагрузки. Точка приложения находится в центре тяжести эпюры. Так для равномерно распределенной на отрезке нагрузки, ее равнодействующая приложена к середине этого отрезка.
- Выбрать систему координат. Ее начало желательно выбрать в точке крепления одной из опор.
- Составить уравнения равновесия.
Векторная сумма всех действующих на тело сил (включая реакции опор) равна нулю:
(1) .
Векторная сумма моментов этих сил относительно начала системы координат O равна нулю:
(2) . - Составить проекции уравнений равновесия (1) и (2) на оси системы координат.
Суммы проекций сил на оси координат равны нулю:
(1.x) ;
(1.y) ;
(1.z) .
Суммы моментов сил относительно координатных осей равны нулю:
(2.x) ;
(2.y) ;
(2.z) . - Для трехмерной задачи мы получим систему из шести уравнений, решая которую, определяем шесть неизвестных проекций реакций опор.
- Для плоской задачи, в которой все действующие силы направлены вдоль осей x и y, получаем три уравнения равновесия: (1.x), (1.y) и (2.z). Из них определяем три неизвестные проекции реакций опор.
- Для упрощения расчетов, иногда бывает полезно спроектировать уравнения равновесия (1) и (2) на другие оси, и составить дополнительные уравнения для моментов относительно других точек. См. Три формы уравнений равновесия твердого тела
- Если полученная система не имеет решения, то при такой схеме закрепления тела равновесие не возможно.
- Если число неизвестных превышает число линейно независимых уравнений, то задача имеет бесконечно много решений, она статически неопределима. Такую задачу можно решить только методами сопротивления материалов. Пример: плоское тело с четырьмя опорами.
Далее мы рассмотрим вопросы, связанные с определением реакций опор твердого тела более подробно и разберем пример решения задачи.
Методы определения реакций опор твердого тела
Рассмотрим некоторое твердое тело, на которое действуют заданные внешние силы. Пусть оно определенным образом закреплено в некоторых точках – опорах, и находится в состоянии равновесия. Эти точки закрепления также называются связями. Это могут быть шарниры, заделки, поверхности и т. п.
Отбросим опоры, и приложим вместо них силы. Они называются силами реакций опор. Их направления определяются устройствами соответствующих опор. В некоторых опорах реакции возникают в виде пары сил, которые задаются значением момента пары. Нам нужно найти такие значения сил реакций, чтобы при их действии на тело, оно покоилось, как это происходит в закрепленном состоянии.
Воспользуемся двумя законами, которые выполняются, если тело находится в покое.
1) Векторная сумма всех действующих на тело внешних сил равна нулю:
(M.1) .
2) Векторная сумма моментов всех внешних сил относительно любой точки O равна нулю:
(M.2) .
Эти законы называются уравнениями равновесия. В них также включены силы (пары сил) реакций опор.
Самый простой способ составления уравнений равновесия
Разберем самый простой способ составления уравнений равновесия. С его помощью можно гарантированно получить значения сил реакций опор или определить, что схема закрепления тела в опорах является статически неопределимой.
Выберем прямоугольную систему координат с началом в любой точке. Часто за начало системы координат удобно выбрать точку крепления одной из опор, но это не обязательно. Итак, пусть мы выбрали систему координат Oxyz с началом в точке O .
Спроектируем (M.1) на оси этой системы. В результате мы получим три уравнения, связывающие проекции сил на оси xyz :
(M.1.x) ;
(M.1.y) ;
(M.1.z) .
Здесь – n сил, действующих на тело. В их состав также включены и силы реакций опор.
Составим уравнения равновесия (M.2) для моментов, относительно осей Ox , Oy , Oz системы координат:
(M.2.x) ;
(M.2.y) ;
(M.2.z) .
Заметим, что эти уравнения являются проекциями векторного уравнения (M.2) на оси Ox , Oy и Oz .
Уравнения (M.1.x), (M.1.y), (M.1.z) и (M.2.x), (M.2.y), (M.2.z) представляют собой полную систему уравнений равновесия твердого тела. Если мы попытаемся добавить сюда еще одно уравнение, то оно будет являться линейной комбинацией уже существующих уравнений, и никак не повлияет на численные значения определяемых реакций опор. Например, мы можем выбрать еще одну ось, и спроектировать на нее уравнение (M.1) для сил. Или мы можем составить уравнение для моментов (M.2) относительно другой точки, отличной от начала координат. В результате получим дополнительные уравнения, но число линейно независимых уравнений от этого не изменится.
Таким образом, для одного тела, методами статики, мы можем составить максимум шесть независимых уравнений равновесия. В некоторых случаях их число может быть еще меньше.
Так, в случае плоской системы сил, у нас будет всего три независимых уравнения. Чтобы в этом убедиться, выберем систему координат, у которой оси Ox и Oy лежат в плоскости действия сил. Ось Oz перпендикулярна. Тогда проекции всех сил на ось Oz равны нулю. Поэтому уравнение (M.1.z) выполняется автоматически, и его можно вычеркнуть. В уравнениях (M.2.x) и (M.2.y) все силы или пересекают оси Ox и Oy, или параллельны им. Поэтому их моменты относительно этих осей равны нулю. Тогда и уравнения (M.2.x) и (M.2.y) выполняется автоматически. Их также можно вычеркнуть. Остаются три уравнения равновесия (M.1.x), (M.1.y) и (M.2.z).
Неизвестными в уравнениях равновесия являются проекции сил реакций опор на оси координат, или проекции пар сил. При решении этих уравнений могут возникнуть следующие случаи.
- Число неизвестных совпадает с числом линейно независимых уравнений. Тогда задача статически определима, и мы можем получить значения неизвестных реакций, решив линейную систему уравнений.
- Число неизвестных меньше числа линейно независимых уравнений и система не имеет решений – при такой схеме закрепления тела равновесие не возможно.
- Число неизвестных превышает число независимых уравнений – система имеет бесконечное множество решений. Выбрать единственное решение, используя только методы статики, нельзя. Задача является статически неопределимой. Такие задачи решаются методами сопротивления материалов. Например, если балка имеет четыре опоры, то у нас минимум четыре неизвестные величины и три уравнения равновесия (для плоской системы сил). В этом случае, для определения реакций, необходимо учитывать возникающие в балке деформации и напряжения.
Эффективные способы составления уравнений равновесия
Уравнений (M.1) и (M.2) достаточно для определения опорных реакций, но иногда бывает удобным дополнить их другими уравнениями, из которых можно определить реакции более легким способом.
Один из способов заключается в соответствующем выборе начала системы координат. Так, если за ее начало взять точку крепления одной из опор тела, то сила реакции в этой опоре будет пересекать начало координат, и поэтому ее момент будет равен нулю (это не относится к паре сил). Тогда компоненты этих сил реакций не будут входить в уравнения для моментов (M.2.x), (M.2.y), (M.2.z).
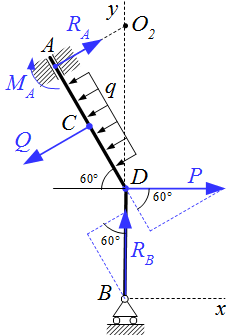
Уравнения (М.1.x) – (М.1.z) представляют собой проекции векторного уравнения (М.1) на оси координат. Но это уравнение можно спроектировать на любую ось. Тогда в него не войдут силы, перпендикулярные выбранной оси. На рисунке слева изображено тело ADB. Реакция в скользящей заделке A состоит из силы RA и пары сил с моментом MA; в опоре на катках B – из силы RB. Для определения только одной реакции RB, мы можем спроектировать уравнение для сил на ось AD (см. рисунок). Поскольку реакция перпендикулярна этой оси, то ее проекция на AD равна нулю. Равномерно распределенная нагрузка q, и ее равнодействующая Q также перпендикулярна AD. В результате получим уравнение, содержащее только одну реакцию RB:
;
;
.
Отсюда сразу определяем RB:
.
Поскольку в равновесии сумма моментов сил равна нулю относительно любой точки, то можно выбрать дополнительную точку, и относительно нее составить уравнение для моментов:
.
Число линейно независимых уравнений при этом не изменится, но мы можем дополнить систему более простым уравнением. См. Три формы уравнений равновесия твердого тела.
Вернемся к нашему примеру ⇑. Пусть нам нужно определить только момент . Тогда можно выбрать точку O2 на пересечении линий действия сил и . Поскольку эти силы пересекают O2, то их моменты относительно этой точки равны нулю. Составим уравнение для моментов:
.
Спроектируем его на ось z, перпендикулярную плоскости рисунка:
;
;
.
Отсюда находим :
.
Для трехмерного распределения сил, уравнения (M.2.x), (M.2.y) и (M.2.z) являются проекциями векторного уравнения для моментов (M.2) на оси координат. Но это уравнение можно спроектировать на любую ось, не обязательно параллельной одной из осей системы координат, как мы делали для сил.
Далее приводится подробно разобранный пример решения задачи, в котором требуемая реакция определяется из одного уравнения за счет соответствующего выбора оси, относительно которой вычисляются суммы моментов сил.
Определение реакций опор твердого тела — решение задачи
Автор: Олег Одинцов . Опубликовано: 30-10-2017 Изменено: 06-01-2022
Условия и уравнения равновесия твердого тела: плоской и пространственной системы сил
Условия равновесия произвольной системы сил
Еще Ньютон говорил, что если геометрическая сумма сил, действующая на тело, равна нулю, то тело:
- либо находится в состоянии покоя;
- либо движется равномерно прямолинейно.
Из теоретической механики известно, что действие нескольких сил, просуммировав, можно заменить равнодействующей силой:
Тогда обязательное условие равновесия можно записать так:
Однако для полного равновесия, часто, этого условия недостаточно, если тело имеет возможность вращаться относительно какой-то точки или оси, то для равновесия такой системы, необходимо, чтобы выполнялось условие:
где M — главные момент системы, который эквивалентен сумме моментов системы относительно некоторого центра.
Условия равновесия плоской системы сил
Выше описанные условия означают, что система будет находится в равновесии, когда все силы, действующие на систему, будут взаимно уравновешиваться и момент относительно любой произвольной точки будет равен нулю, отсюда вытекает первая и основная форма условий равновесия для плоской системы сил:
Вторая форма условий равновесия записывается следующим образом:
Важно! Ось не должна быть перпендикулярна прямой AB.
И, наконец, третья форма условий равновесия выглядит так:
Из данной системы уравнений следует, что для равновесия системы достаточно равенства нулю суммы моментов относительно трех точек.
Важно! Точки, относительно которых записываются уравнения не должны лежать на одной прямой.
Уравнения равновесия для плоской системы сил
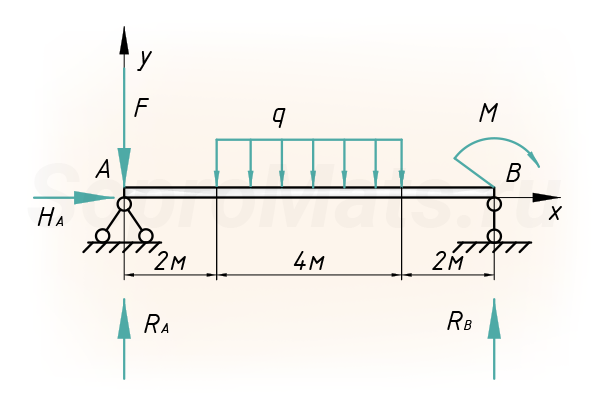
Рассмотрим на примере плоской балки, как записываются уравнения равновесия. Использовать будет классическую (первую) форму условия равновесия:
Сумма моментов относительно точки A:
Сумма проекций всех сил на вертикальную ось (y):
Сумма проекций всех сил на горизонтальную ось(x):
Условие равновесия пространственной системы сил
Для пространственной системы сил условие равновесие выглядит вот так:
Таким образом, пространственная система будет находиться в равновесии, если суммы проекций сил на координатные оси, а также суммы моментов относительно осей будут равны нулю.
Уравнения равновесия для пространственной системы сил
В качестве примера рассмотрим пространственную раму, закруженную сосредоточенными силами. Составим для нее шесть уравнений равновесия:
http://1cov-edu.ru/mehanika/statika/opredelenie-reaktsij-opor-tverdogo-tela/
http://sopromats.ru/sopromat/usloviya-uravneniya-ravnovesiya/