Как составлять уравнение плоскости в отрезках

Уравнение плоскости в отрезках

В данной статье мы рассмотрим уравнение плоскости в отрезках. Представим методы преобразования уравнения плоскости в отрезках в уравнение плоскости в общем виде и обратно. Рассмотрим численные примеры.

Уравнение плоскости в отрезках представляется следующей формулой:

,

(1)

где a, b, c отличные от нуля числа.

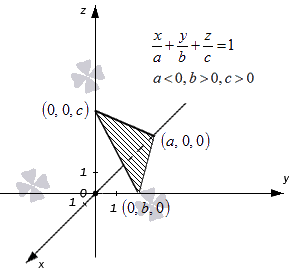
Отметим, что числа a, b, c в уравнении (1) имеют простой геометрический смысл. Они равны длинам отрезков, которые отсекает плоскость на осях Ox, Oy, Oz (Рис.1, Рис.2).

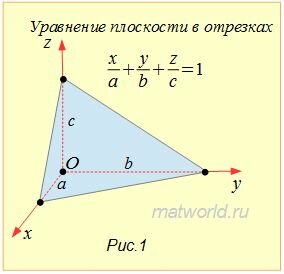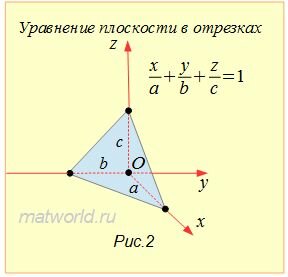Действительно. Подставляя в (1) y=0, z=0 получим x=a, если же подставить в (1) x=0, y=0 то получим z=c, подставвляя, наконец, x=0, z=0 получим y=b. Таким образом плоскость, определяемая уравнением (1) проходит через точки M₁(a, 0, 0), M₂(0, b, 0) и M₃(0, 0, с).

Пример 1. Составить уравнение прямой, которая пересекает оси Ox, Oy и Oz в точках −1,3 и 7, соответственно.

Решение. Подставляя значения a=−1, b=3 и c=7 в (1), получим:

.

.

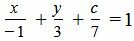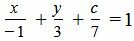Приведение уравнения плоскости в отрезках к общему виду

Левая часть уравнения (1) приведем к общему знаменателю:

.

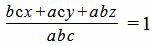Далее, умножив обе части уравнения на abc, получим:

.

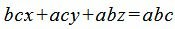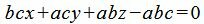Пример 2. Уравнение плоскости в отрезках представлено следующим уравнением:

.

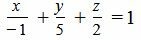Перевести уравнение к общему виду.

Решение. Приведем левую часть уравнения к общему знаменателю:

.

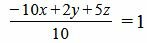Умножив обе части уравнения на 10, получим:

.

.

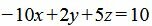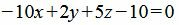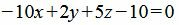Приведение общего уравнения плоскости к уравнению плоскости в отрезках

где A, B, C, D − отличные от нуля числа, т.е. уравнение плокости является полным (о полных и неполных уравнениях плоскости смотрите здесь).

Сделаем следующие преобразования. Переведем свободный член D на правую часть уравнения и разделим обе части уравнения на −D:

.

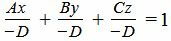(2)

Уравнение (2) можно переписать в следующем виде:

.

(3)

Сделаем следующие обозначения:

Тогда получим уравнение прямой в отрезках (1).

Пример 3. Привести общее уравнение прямой

к уравнению прямой в отрезках.

Решение. Так как все коэффициенты уравнения отличны от нуля, можно построить уравнение плоскости в отрезках. Воспользуемся формулой (3). Имеем: A=−2, B=3, C=5, D=−4. Подставив эти значения в формулу (3), получим:

Уравнение плоскости в отрезках: описание, примеры, решение задач

Данный раздел будет полностью посвящен теме «Уравнение плоскости в отрезках». Мы последовательно рассмотрим, какой вид имеет уравнение плоскости в отрезках, применение этого уравнения для построения заданной плоскости в прямоугольной системе координат, переход от общего уравнения плоскости к уравнению плоскости в отрезках. В статье мы рассмотрим большое количество примеров, которые облегчат усвоение информации.

Уравнение плоскости в отрезках – описание и примеры

Уравнение плоскости в отрезках имеет вид x a + y b + z c = 1 , где a , b и c – это действительные числа, отличные от нуля. Абсолютные величины чисел a , b и c равны длинам отрезков, которые отсекаются плоскостью на осях координат O х , O у и O z в трехмерной системе координат O х у z . Откладываются длины отрезков от начала координат. Направление, в котором необходимо отложить длину отрезка, определяет знак, стоящий перед числом. Наличие «-» свидетельствует о том, что отрезок надо откладывать от нуля в отрицательном направлении оси.

Действительно, координаты точек a , 0 , 0 , 0 , b , 0 , 0 , 0 , c удовлетворяют уравнению плоскости в отрезках:

a a + 0 b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + b b + 0 c = 1 = 1 ⇔ 1 = 1 0 a + 0 b + c c = 1 = 1 ⇔ 1 = 1

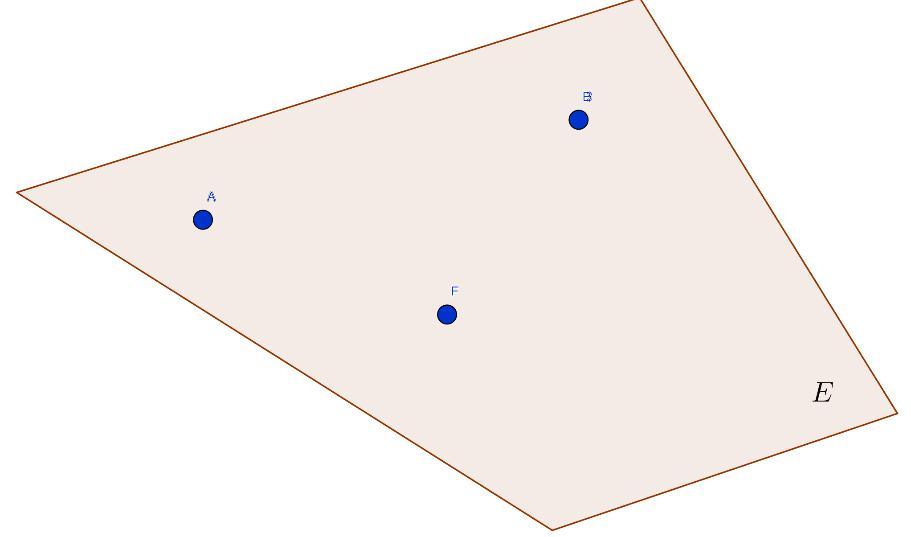
Поясним этот момент, расположив заданные точки на графике.

Проиллюстрируем описанное выше примером.

Плоскость проходит через точки — 2 , 0 , 0 , 0 , 3 , 0 и 0 , 0 , — 1 2 на осях координат в прямоугольной системе координат O x y z . Необходимо записать уравнение плоскости в отрезках.

Решение

Определим положение отрезков, отсекаемых плоскостью на осях координат. На оси абсцисс откладываем в отрицательном направлении отрезок длиной 2 единицы. На оси ординат в положительном направлении откладываем отрезок длиной 3 . На оси аппликат в отрицательном направлении откладываем отрезок длиной 1 2 .

При этом, уравнение плоскости в отрезках будет иметь вид: x — 2 + y 3 + z — 1 2 = 1 .

Ответ: x — 2 + y 3 + z — 1 2 = 1

Уравнение плоскости в отрезках удобно использовать для построения чертежей. Проиллюстрируем это утверждение примером.

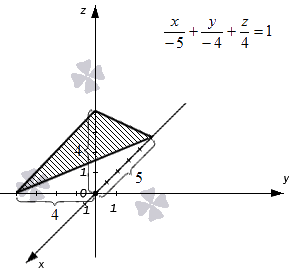
Плоскость в прямоугольной системе координат O х у z задана уравнением плоскости в отрезках вида x — 5 + y — 4 + z 4 = 1 . Необходимо изобразить эту плоскость на графике.

Решение

Изобразим оси координат, обозначаем начало координат и единичные отрезки на осях. Отмечаем длины отрезков, отсекаемых плоскостью, на каждой из осей. Соединяем концевые точки отрезков прямыми линиями. Полученная плоскость имеет вид треугольника. Она соответствует заданному уравнению плоскости в отрезках x — 5 + y — 4 + z 4 = 1 .

Ответ:

Плоскость может быть задана уравнением плоскости другого вида. Для того, чтобы изобразить заданную плоскость на чертеже, можно сначала перейти к уравнению плоскости в отрезках. Получив уравнение плоскости в отрезках, нам останется лишь отметить точки a , 0 , 0 , 0 , b , 0 , 0 , 0 , c и соединить их прямыми линиями.

Приведение общего уравнения плоскости к уравнению плоскости в отрезках

Мы имеем общее уравнение плоскости в пространстве вида A x + B y + C z + D = 0 . И мы можем получить уравнение плоскости в отрезках. Сделать это можно в том случае, если плоскость пересекает все координатные оси, причем не в начале координат.

Не получится перевести общее уравнение плоскости в пространстве в уравнение плоскости в отрезках в тех случаях, когда плоскость проходит через одну из координатных осей или располагается параллельно оси. Другими словами, мы можем работать лишь с полным уравнением плоскости вида A x + B y + C z + D = 0 , где A ≠ 0 , B ≠ 0 , C ≠ 0 , D ≠ 0 .

Приведение общего уравнения плоскости к уравнению плоскости в пространстве производится следующим образом. Переносим слагаемое D в правую часть уравнения с противоположным знаком.

A x + B y + C z + D = 0 ⇔ A x + B y + C z = — D

Так как D ≠ 0 , то обе части полученного уравнения можно разделить на – D : A — D x + B — D y + C — D z = 1 .

Так как A ≠ 0 , B ≠ 0 , C ≠ 0 , то мы можем отправить в знаменатели коэффициенты перед переменными x , y и z . Последнее уравнение эквивалентно равенству x — D A + y — D B + z — D C = 1 . При этом мы использовали очевидное равенство p q = 1 q p , p , q ∈ R , p ≠ 0 , q ≠ 0 .

В итоге, мы получаем уравнение плоскости в отрезках. Это становится хорошо видно в том случае, если обозначить — D A = a , — D B = b , — D C = c .

Разберем решение примера.

Плоскость в прямоугольной системе координат O x y z в пространстве задана уравнением вида 3 x + 9 y — 6 z — 6 = 0 . Переведем это уравнение в уравнение плоскости в отрезках.

Решение

Данное в условии задачи уравнение является полным уравнением плоскости. Это дает нам возможность привески его к уравнению плоскости в отрезках. Перенесем — 6 в правую часть равенства, а затем разделим обе части равенства на 6 :

3 x + 9 y — 6 z — 6 = 0 ⇔ 3 x + 9 y + 6 z = 6 3 x + 9 y — 6 z = 6 ⇔ 1 2 x + 3 2 y — z = 1

Коэффициенты при переменных x, y и z отправим в знаменатели: 1 2 x + 3 2 y — z = 1 ⇔ x 2 + y 2 3 + z — 1 = 1 . Полученное уравнение и есть уравнение плоскости в отрезках.

Ответ: x 2 + y 2 3 + z — 1 = 1

Уравнение плоскости в отрезках. Примеры решения задач

Для определения параллельности и перпендикулярности плоскостей, а также для расчета расстояний между этими геометрическими объектами, удобно пользоваться тем или иным видом числовых функций. Для каких задач удобно использовать уравнение плоскости в отрезках? В данной статье рассмотрим, что это и как использовать в практических заданиях.

Что собой представляет уравнение в отрезках?

Плоскость можно задать в трехмерном пространстве несколькими способами. В данной статье некоторые из них будут приведены во время решения задач различного типа. Здесь же дадим подробную характеристику уравнению в отрезках плоскости. Оно в общем случае имеет следующий вид:

Вам будет интересно: Значение и происхождение фамилии Федоров

Где символами p, q, r обозначены некоторые конкретные числа. Это уравнение можно легко перевести в выражение общего вида и в другие формы числовых функций для плоскости.

Удобство записи уравнения в отрезках заключается в том, что оно содержит явные координаты пересечения плоскости с перпендикулярными осями координат. На оси x относительно начала координат плоскость отсекает отрезок длиною p, на оси y — равную q, на z — длиною r.

Если какой-либо из трех переменных не содержится в уравнении, то это означает, что через соответствующую ось плоскость не проходит (математики говорят, что пересекает в бесконечности).

Далее приведем несколько задач, в которых покажем, как работать с этим уравнением.

Связь общего и в отрезках уравнений

Известно, что плоскость задана следующим равенством:

2*x — 3*y + z — 6 = 0.

Необходимо это общее уравнение плоскости в отрезках записать.

Когда возникает подобная задача, нужно следовать такой методике: переносим свободный член в правую часть равенства. Затем делим на этот член все уравнение, стремясь его выразить в виде, приведенном в предыдущем пункте. Имеем:

2*x/6 — 3*y/6 + z/6 = 1 =>

Мы получили в отрезках уравнение плоскости, заданное изначально в общем виде. Заметно, что плоскость отсекает отрезки с длинами 3, 2 и 6 для осей x, y и z соответственно. Ось y плоскость пересекает в отрицательной области координат.

При составлении уравнения в отрезках важно, чтобы перед всеми переменными стоял знак «+». Только в этом случае число, на которое эта переменная делится, покажет отсекаемую на оси координату.

Нормальный вектор и точка на плоскости

Известно, что некоторая плоскость имеет направляющий вектор (3; 0; -1). Также известно, что она проходит через точку (1; 1; 1). Следует для этой плоскости написать уравнение в отрезках.

Чтобы решить эту задачу, следует для начала воспользоваться общей формой для этого двумерного геометрического объекта. Общая форма записывается в виде:

A*x + B*y + C*z + D = 0.

Три первых коэффициента являются здесь координатами вектора направляющего, который задан в условии задачи, то есть:

Остается найти свободный член D. Его определить можно по такой формуле:

D = -1*(A*x1 + B*y1 + C*z1).

Где значения координат с индексом 1 соответствуют координатам точки, принадлежащей плоскости. Подставляем их значения из условия задачи, получаем:

D = -1*(3*1 + 0*1 + (-1)*1) = -2.

Теперь можно записать полностью уравнение:

Выше уже была продемонстрирована методика преобразования этого выражения в уравнение в отрезках плоскости. Применим ее:

Ответ на задачу получен. Заметим, что данная плоскость пересекает только x и z оси. Для y она параллельна.

Две прямые, задающие плоскость

Из курса пространственной геометрии каждый школьник знает, что две произвольные прямые задают однозначно плоскость в пространстве трехмерном. Решим подобную задачу.

Известны два уравнения прямых:

(x; y; z) = (1; 0; 0) + α*(2; -1; 0);

(x; y; z) = (1; -1; 0) + β*(-1; 0; 1).

Нужно записать в отрезках уравнение плоскости, через прямые эти проходящей.

Так как обе прямые должны лежать в плоскости, то это означает, что их вектора (направляющие) должны быть перпендикулярны вектору (направляющему) для плоскости. В то же время известно, что векторное произведение произвольных двух направленных отрезков дает результат в виде координат третьего, перпендикулярного двум исходным. Учитывая это свойство, получаем координаты нормального к искомой плоскости вектора:

Поскольку его можно умножать на произвольное число, при этом образуется новый направленный отрезок, параллельный исходному, то можно знак полученных координат заменить на противоположный (умножить на -1), получим:

Нам известен направляющий вектор. Остается взять произвольную точку одной из прямых и составить общее уравнение плоскости:

D = -1*(1*1 + 2*0 + 3*0) = -1;

Переводим это равенство в выражение в отрезках, получаем:

Таким образом, плоскость пересекает все три оси в положительной области координатной системы.

Три точки и плоскость

Так же как две прямые, три точки задают плоскость однозначно в трехмерном пространстве. Запишем соответствующее уравнение в отрезках, если известны следующие координаты точек, лежащих в плоскости:

Поступим следующим образом: вычислим координаты двух произвольных векторов, соединяющих эти точки, затем, найдем нормальный к плоскости вектор n¯, рассчитав произведение найденных направленных отрезков. Получаем:

QP¯ = P — Q = (1; -1; 0);

QM¯ = M — Q = (2; 4; 0);

n¯ = [QP¯*QM¯] = [(1; -1; 0)*(2; 4; 0)] = (0; 0; 6).

Возьмем для примера точку P, составим уравнение плоскости:

D = -1*(0*2 + 0*(-3) + 6*0) = 0;

Мы получили простое выражение, которое соответствует плоскости xy в данной прямоугольной системе координат. Записать его в отрезках нельзя, поскольку оси x и y принадлежат плоскости, а длина отсекаемого на оси z отрезка равна нулю (точка (0; 0; 0) принадлежит плоскости).