Как составлять уравнения с 3 элементами

Система линейных уравнений с тремя переменными

Линейное уравнение с тремя переменными и его решение

Уравнение вида ax+by+cz = d , где a, b, c, d — данные числа, называется линейным уравнением с тремя переменными x, y и z.

Например: $2x+5y+z = 8; -x+1, 5y+2z = 0; \frac<1> <2>x-8y-5z = 7$

Уравнение с тремя переменными может быть не только линейным, т.е. содержать не только первые степени переменных x,y и z.

Например: $2x^2+xz+y^2+yz^2 = 3,x-5y^2+z^3 = 1, 7x^3+y+xyz = 7$

Решением уравнения с тремя переменными называется упорядоченная тройка значений переменных (x,y,z), обращающая это уравнение в тождество.

О тождествах – см. §3 данного справочника

Например: для уравнения 2x+5y+z=8 решениями являются тройки x = -2, y = 1, z = 7; x = -1, y = 1, 6 , z = 2; x = -3, y = 2, 4, z = 2 и т.д. Уравнение имеет бесконечное множество решений.

Геометрическим представлением линейного уравнения с тремя переменными является плоскость в трёхмерном координатном пространстве .

Решение системы линейных уравнений с тремя переменными методом подстановки

Алгоритм метода подстановки для системы уравнений с тремя переменными аналогичен алгоритму для двух переменных (см.§45 данного справочника)

Например: решить систему

$$ <\left\< \begin 3x+2y-z = 8 \\ x-y+z = -2 \\ 2x-3y-5z = 1 \end \right.> \Rightarrow <\left\< \begin 3(y-z-2)+2y-z = 8 \\ x = y-z-2 \\ 2(y-z-2)-3y-5z = 1 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin x = y-z-2 \\ 5y-4z = 14 \\ -y-7z = 5 \end \right.> \Rightarrow <\left\< \begin x = y-z-2 \\ y = -7z-5 \\ 5(-7z-5)-4z = 14 \end \right.> \Rightarrow <\left\< \begin x = y-z-2 \\ y = -7z-5 \\ -39z = 39 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin x = 2-(-1)-2 = 1 \\ y = -7\cdot(-1)-5 = 2 \\ z = -1 \end \right.> \Rightarrow <\left\< \begin x = 1 \\ y = 2 \\ z = -1 \end \right.> $$

Решение системы линейных уравнений с тремя переменными методом Крамера

Для системы с 3-мя переменными действуем по аналогии.

Дана система 3-х линейных уравнений с 3-мя переменными:

$$ <\left\< \begin a_1 x+b_1 y+c_1 z = d_1 \\ a_2 x+b_2 y+c_2 z = d_2 \\ a_3 x+b_3 y+c_3 z = d_3 \end \right.> $$

Определим главный определитель системы:

$$ \Delta = \begin a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end $$

и вспомогательные определители :

$$ \Delta_x = \begin d_1 & b_1 & c_1 \\ d_2 & b_2 & c_2 \\ d_3 & b_3 & c_3 \end, \Delta_y = \begin a_1 & d_1 & c_1 \\ a_2 & d_2 & c_2 \\ a_3 & d_3 & c_3 \end, \Delta_z = \begin a_1 & b_1 & d_1 \\ a_2 & b_2 & d_2 \\ a_3 & b_3 & d_3 \end $$

Тогда решение системы:

Соотношение значений определителей, расположения плоскостей и количества решений:

Три плоскости пересекаются в одной точке

Три плоскости параллельны

Две или три плоскости совпадают или пересекаются по прямой

Бесконечное множество решений

Осталось определить правило вычисления определителя 3-го порядка.

Таких правил несколько, приведём одно из них (так называемое «раскрытие определителя по первой строке»):

$$ \Delta = \begin a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \\ a_3 & b_3 & c_3 \end = a_1 = \begin b_2 & c_2 \\ b_3 & c_3 \end — b_1 = \begin a_2 & c_2 \\ a_3 & c_3 \end + c_1 = \begin a_2 & b_2 \\ a_3 & b_3 \end = $$

$$ = a_1 (b_2 c_3-b_3 c_2 )-b_1 (a_2 c_3-a_3 c_2 )+c_1 (a_2 b_3-a_3 b_2 )$$

Примеры

Пример 1. Найдите решение системы уравнений методом подстановки:

$$<\left\< \begin z = 3x+2y-13 \\ 2x-y+3(3x+2y-13) = -2 \\ x+2y-(3x+2y-13) = 9 \end \right.> \Rightarrow <\left\< \begin z = 3x+2y-13 \\ 11x+5y = 37 \\ -2x = -4 \end \right.> \Rightarrow $$

$$\Rightarrow <\left\< \begin z = 3\cdot2+2\cdot3-13 = -1 \\ y = \frac<37-11\cdot2> <5>= 3 \\ x = 2 \end \right.> \Rightarrow <\left\< \begin x = 2 \\ y = 3 \\ z = -1 \end \right.> $$

$$ <\left\< \begin x = -y-3z+6 \\ 2(-y-3z+6)-5y-z = 5\\ (-y-3z+6)+2y-5z = -11 \end \right.> \Rightarrow <\left\< \begin x = -y-3z+6 \\ -7y-7z = -7 |:(-7) \\ y-8z = -17 \end \right.> \Rightarrow $$

$$ \Rightarrow <\left\< \begin x = -y-3z+6 \\ y+z = 1 \\ y-8z = -17 \end \right.> \Rightarrow <\left\< \begin x = -y-3z+6 \\ 9z = 18 \\ y = 1-z \end \right.> \Rightarrow <\left\< \begin x = 1-6+6 = 1 \\ z = 2 \\ y = 1-2 = -1 \end \right.> \Rightarrow$$

Пример 2. Найдите решение системы уравнений методом Крамера:

$$ \Delta = \begin 3 & 2 & -1 \\ 2 & -1 & 3\\ 1 & 2 & -1 \end = 3 = \begin -1 & 3 \\ 2 & -1 \\ \end — 2 = \begin 2 & 3 \\ 1 & -1 \\ \end — 1 = \begin 2 & -1 \\ 1 & 2 \\ \end = $$

$$ \Delta_x = \begin 13 & 2 & -1 \\ -2 & -1 & 3 \\ 9 & 2 & -1 \\ \end = 13 = \begin -1 & 3 \\ 2 & -1 \\ \end — 2 = \begin -2 & 3 \\ 9 & -1 \\ \end — 1 = \begin -2 & -1 \\ 9 & 2 \\ \end = $$

$$ \Delta_y = \begin 3 & 13 & -1 \\ 2 & -2 & 3 \\ 1 & 9 & -1 \\ \end = 3 = \begin -2 & 3 \\ 9 & -1 \\ \end — 13 = \begin 2 & 3 \\ 1 & -1 \\ \end — 1 = \begin 2 & -2 \\ 1 & 9 \\ \end = $$

$$ \Delta_z = \begin 3 & 2 & 13 \\ 2 & -1 & -2 \\ 1 & 2 & 9 \\ \end = 3 = \begin -1 & -2 \\ 2 & 9 \\ \end — 2 = \begin 2 & -2 \\ 1 & 9 \\ \end + 13 = \begin 2 & -1 \\ 1 & 2 \\ \end = $$

$$ \Delta = \begin 1 & 1 & 3 \\ 2 & -5 & -1\\ 1 & 2 & -5 \end = 1 = \begin -5 & -1 \\ 2 & -5 \\ \end — 1 = \begin 2 & -1 \\ 1 & -5 \\ \end + 3 = \begin 2 & -5 \\ 1 & 2 \\ \end = $$

$$ \Delta_x = \begin 6 & 1 & 3 \\ 5 & -5 & -1 \\ -11 & 2 & -5 \\ \end = 6 = \begin -5 & -1 \\ 2 & -5 \\ \end — 1 = \begin 5 & -1 \\ -11 & -5 \\ \end + 3 = \begin 5 & -5 \\ -11 & 2 \\ \end = $$

$$ = 6(25+2)—(-25-11)+3(10-55) = 162+36-135 = 63 $$

$$ \Delta_y = \begin 1 & 16 & 3 \\ 2 & 5 & -1 \\ 1 & -11 & -5 \\ \end = 1 = \begin 5 & -1 \\ -11 & -5 \\ \end — 6 = \begin 2 & -1 \\ 1 & -5 \\ \end + 3 = \begin 2 & 5 \\ 1 & -11 \\ \end = $$

$$ \Delta_z = \begin 1 & 1 & 6 \\ 2 & -5 & 5 \\ 1 & 2 & -11 \\ \end = 1 = \begin -5 & 5 \\ 2 & -11 \\ \end — 1 = \begin 2 & 5 \\ 1 & -11 \\ \end + 6 = \begin 2 & -5 \\ 1 & 2 \\ \end = $$

Пример 3*. Решите систему уравнений относительно x,y,и z:

$$ a \neq b, b \neq c, a \neq c $$

Решаем методом замены:

$$ <\left\< \begin z = -(a^3+a^2 x+ay)\\ b^3+b^2 x+by-(a^3+a^2 x+ay) = 0 \\ c^3+c^2 x+cy-(a^3+a^2 x+ay) = 0 \end \right.> \Rightarrow <\left\< \beginz = -(a^3+a^2 x+ay)\\ (b^2-a^2 )x+(b-a)y = a^3-b^3 \\ (c^2-a^2 )x+(c-a)y = a^3-c^3 \end \right.> $$

Т.к. $ a \neq b$ второе уравнение можно сократить на $(a-b) \neq 0$

Т.к.$ a \neq c$ третье уравнение можно сократить на $(a-с) \neq 0 $. В третьем уравнении после сокращения поменяем знаки:

Из второго уравнения получаем:

Т.к. $b \neq c$ можно сократить на $(b-c) \neq 0$:

$$ z = -(a^3+a^2 x+ay) = -a^3+a^2 (a+b+c)-a(ab+ac+bc) = $$

$$ = -a^3+a^3+a^2 b+a^2 c-a^2 b-a^2 c-abc = -abc $$

Системы линейных уравнений с тремя переменными

Линейным уравнением называется уравнение вида:

В этом уравнении — неизвестные, а — действительные (или комплексные) числа. При этом называются коэффициентами уравнения, а — свободным членом.

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

Из трех способов решения этих систем: графического, способа подстановки и способа сложения остается два последних способа. Графический способ уже не проходит, так как пришлось бы находить точку пересечения трех плоскостей. А это трудно изобразить.

Способ подстановки для трех уравнений похож на способ подстановки для двух уравнений с двумя неизвестными, только у этого способа на один шаг больше. Первое: выражаем одно из неизвестных из одного уравнения через два остальных неизвестных и подставляем это выражение в оставшиеся два уравнения. Эти оставшиеся два уравнения составляют систему из двух уравнений с двумя неизвестными. А дальше решаем эту полученную систему и находим два неизвестных, а затем, зная их, и третье неизвестное.

Пример 1 Решить систему уравнений: способом подстановки.

Выразим из первого уравнения через остальные неизвестные и свободный член. Найденное выражение подставим в остальные уравнения.

Далее, оставляя первое уравнение в покое, решаем систему из двух получившихся уравнений с неизвестными и (предварительно разделив обе части второго уравнения на ).

Получили единственное решение системы

Рассмотрим теперь способ сложения. Так же как и для двух уравнений с двумя неизвестными, нужно при помощи сложения уравнений добиться, чтобы одно из неизвестных пропало.Приведем пример.

Пример 2 Решить систему уравнений: способом сложения.

Постараемся получить два уравнения с двумя неизвестными. Избавимся от неизвестной . Для этого удвоенное первое уравнение сложим почленно с удвоенным вторым уравнением, а удвоенное второе уравнение прибавим к третьему уравнению:

Далее производим почленное сложение двух уравнений с двумя неизвестными, исключая неизвестную :

Из последнего уравнения системы находим . Подставляя найденное значение во второе уравнение, находим . Наконец из первого уравнения находим . Итак — единственное решение системы.

В заключении решим задачу, которая приводится к системе с тремя неизвестными.

Задача В трех урнах — шариков. В первой урне шариков больше чем во второй на столько, сколько шариков в третьей урне. Число шариков во второй урне относится к числу шариков в третьей урне как . Сколько шариков в каждой урне?

Обозначим число шариков в 1-й, 2-й и 3-й урнах через соответственно. Тогда первое условие задачи дает уравнение , второе условие — , а третье условие — . Запишем три полученные уравнения в систему, сделав предварительно третье уравнение линейным:

Складывая почленно первые два уравнения находим .Решаем систему из двух оставшихся уравнений:

Итак, в урнах соответственно и шариков.

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Как решать химические уравнения — схемы и примеры решения для разных реакций

Основные термины и понятия

Составление уравнений химических реакций невозможно без знания определённых обозначений, показывающих, как проходит реакция. Объединение атомов, имеющих одинаковый ядерный заряд, называют химическим элементом. Ядро атома состоит из протонов и нейтронов. Первые совпадают с числом атомного номера элемента, а значение вторых может варьироваться. Простейшими веществами называют элементы, состоящие из однотипных атомов.

Любой химический элемент описывается с помощью символов, условно обозначающих структуру веществ. Формулы являются неотъемлемой частью языка науки. Именно на их основе составляют уравнения и схемы. По своей сути они отражают количественный и качественный состав элементов. Например, запись HNO3 сообщает, что в соединении содержится одна молекула азотной кислоты, а оно само состоит из водорода, азота и кислорода. При этом в состав одного моля азотной кислоты входит по одному атому водорода и азота и 3 кислорода.

Символика элементов, условное обозначение, представляет собой химический язык. В значке содержится информация о названии, массовом числе и порядковом номере. Международное обозначение принято, согласно периодической таблице Менделеева, разработанной в начале 1870 года.

Взаимодействующие между собой вещества называются реагентами, а образующиеся в процессе реакции — продуктами. Составление и решение химических уравнений фактически сводится к определению результатов реакций, поэтому просто знать формулы веществ мало, нужно ещё уметь подбирать коэффициенты. Располагаются они перед формулой и указывают на количество молекул или атомов, принимающих участие в процессе. С правой стороны от химического вещества ставится индекс, указывающий место элемента в системе.

Записывают уравнения в виде цепочки, в которой указываются все стадии превращения вещества начиная с левой части. Вначале пишут формулы элементов в исходном состоянии, а затем последовательно их преобразование.

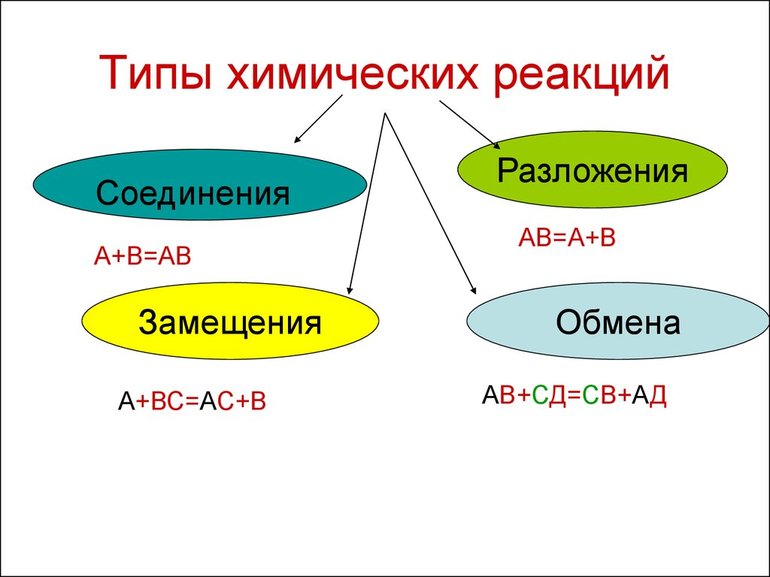
Виды химических реакций

Химические явления характеризуются тем, что из двух и более элементов образуются новые вещества. Уравнения описывают эти процессы. Впервые с объяснениями протекания реакций знакомят в восьмом классе средней образовательной школы на уроках неорганической химии. Ученикам демонстрируют опыты, в которых явно наблюдаются различия в протекании реакций.

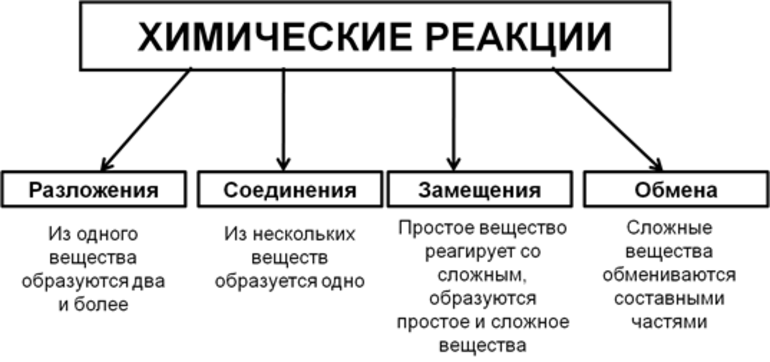
Всего существует 4 типа химического взаимодействия веществ:

1. Соединение. В реакцию могут вступать 2 простых вещества: металл и неметалл или неметалл и неметалл. Например, алюминий с серой образуют сульфид алюминия. Кислород, взаимодействуя с водородом, превращается в воду. Объединятся могут 2 оксида с растворимым основанием, как оксид кальция с водой: CaO + H2O = Ca (OH)2 или основной оксид с кислотным: CaO + SO3 = CaSO4.
2. Разложение. Это процесс обратный реакции соединения: было одно вещество, а стало несколько. Например, при пропускании электрического тока через воду получается водород и кислород, а при нагревании известняка 2 оксида: CaCO3 = CaO + CO2.
3. Замещение. В реакцию вступают 2 элемента. Один из них простой, а второй сложный. В итоге образуются 2 новых соединения, при котором атом простого вещества заменяет сложный, как бы вытесняя его. Условие протекания процесса: простое вещество должно быть более активным, чем сложное. Например, Zn + 2HCl = ZnCl2 + H2. Величину активности можно узнать из таблицы ряда электрохимических напряжений.
4. Обмен. В этом случае между собой реагируют 2 сложных элемента, обменивающиеся своими составными частями. Условием осуществления такого типа реакции является обязательное образование воды, газа или осадка. Например, CuO + 2HCl = CuCl2 + H2O. Чтобы узнать, смогут ли вещества прореагировать, используют таблицу растворимости.

Основными признаками химических реакций является изменение цвета, выделение газа или образование осадка. Различают их по числу веществ, вступивших в реакцию и образовавшихся продуктов. Правильное определение типа реакции особо важно при составлении химических уравнений, а также определения свойств и возможностей веществ.

Окислительно-восстановительный процесс

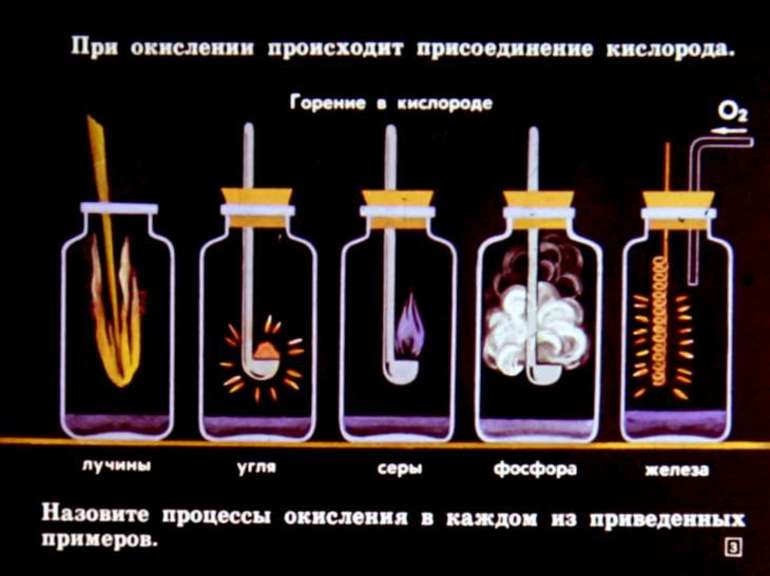
Составление большинства реакций сводится к подбору коэффициентов. Но при этом могут возникнуть трудности с установлением равновесия, согласно закону сохранения массы веществ. Чаще всего такая ситуация возникает при решении заданий, связанных с расстановкой количества атомов в уравнениях окислительно-восстановительных процессов.

Под ними принято понимать превращения, протекающие с изменением степени окисления элементов. При окислении происходит процесс передачи атомом электронов, сопровождающийся приобретением им положительного заряда или ионом, после чего он становится нейтральным. При этом также происходит процесс восстановления, связанный с присоединением элементарных частиц атомом.

Для составления уравнений необходимо определить восстановитель, окислитель и число участвующих в реакции электронов. Коэффициенты же подбирают с помощью метода электронно-ионного баланса (полуреакций). Его суть состоит в установлении равенства путём уравнивания количества электронов, отдаваемых одним элементом и принимаемым другим.

Классический алгоритм

В основе решения задач этим методом — закон сохранения массы. Согласно ему, совокупная масса элементов до реакции и после остаётся неизменной. Другими словами, происходит перегруппировка частиц. Если рассматривать решение химического уравнения поэтапно, оно будет состоять из трёх шагов:

1. Написания формул элементов, вступающих в реакцию с левой стороны.
2. Указания справа формулы образующихся веществ.
3. Уравнивания числа атомов с добавлением коэффициентов.

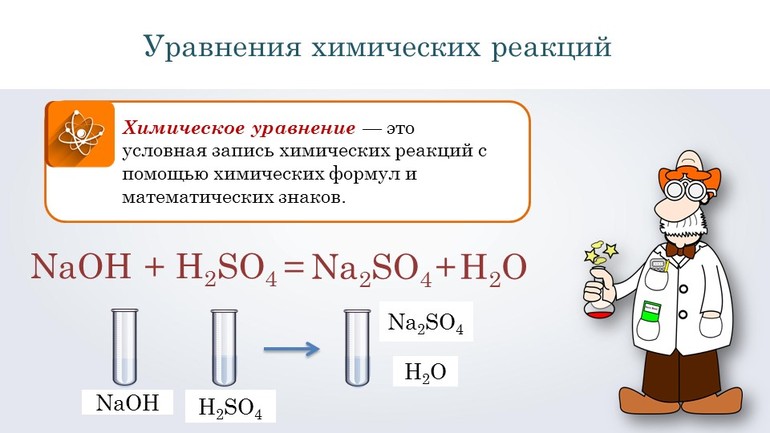
Перед тем как переходить к сложным соединениям, лучше всего потренироваться на простых. Например, нужно составить уравнение, описывающее взаимодействие двух сложных веществ: гидроксида натрия и серной кислоты. При таком соединении образуется сульфат натрия и вода.

Согласно алгоритму, в левой части уравнения необходимо записать реагенты, а в правой продукты реакции: NaOH + H2SO 4 → Na 2SO4 + H2O. Теперь следует уравнять коэффициенты. Начинают с первого элемента. В примере это натрий. В правой части содержится 2 его атома, а в левой один, поэтому необходимо возле реагента поставить цифру 2. Затем нужно уровнять водород. В результате получится выражение: 2 NaOH + H2SO 4 → Na2 SO4 +2H2O.

Ещё одним наглядным примером является процесс реакции тринитротолуола с кислородом. При их взаимодействии образуется: C7H5N3O6 + O2 → CO2 + H2O + N2. Исходя из того, что слева находится нечётное число атомов H и N, а справа чётное, нужно их уравнять: 2C7H5N3O6 + O2 → CO2 + H2O + N2.

Теперь становится понятным, что 14 и 10 атомов углерода и водорода должны образовать 14 долей диоксида и 5 молекул воды. При этом 6 атомов азота превратятся в 3. Итоговое уравнение будет выглядеть как 2C7H5N3O6 + 10,5O2 → 14CO2 + 5H2O + 3N2.

Перед тем как начинать тренировку по составлению уравнений, следует научиться расставлять валентность. Это параметр, равный числу соединившихся атомов каждого элемента. Фактически это способность к соединению. Например, в формуле NH3 валентность атома азота равна 3, а водорода 1.

Решение методом полуреакций

Алгоритм для решения примеров химических уравнений проще рассмотреть на конкретном задании. Пускай необходимо описать процесс окисления пирита азотной кислоты с малой концентрацией: FeS2 + HNO3. Решать этот пример необходимо в следующей последовательности:

1. Определить продукты реакции. Так как кислота является сильным окислителем, сера получит максимальную степень оксидации S6+, а железо Fe3+. HNO3 может восстановиться до одного из двух состояний NO2 или NO.
2. Исходя из состава ионов и правила, что вещества, переходящие в газовую форму или плохо растворимые, записываются в молекулярном виде, верным будет записать: FeS2 — Fe3+ + 2SO2−4. Гидролизом можно пренебречь.
3. В записи уравнивают кислород. Для этого в левую часть добавляют 8 молекул воды, а в правую 16 ионов водорода: FeS2 + 8H20 — Fe3+ + 2SO2−4 + 16H+. Так как заряда в левой части нет, а в правой он равный +15, то серное железо должно будет отдать 15 электронов. Значит, уравнение примет вид: FeS2 + 8H20 — 15e → Fe3+ + 2SO2−4 + 16H+.
4. Теперь переходят к реакции восстановления нитрата иона: NO-3 →NO. Для её составления нужно отнять у оксида азота 2 атома кислорода. Делают это путём прибавления к левой части 4 ионов водорода, а правой — 2 молекул воды. В итоге получится: NO-3 + 4H+ → NO + 2H2O.
5. Полученную формулу уравнивают добавлением к левой части 3 электронов: NO-3 + 4H+ 3e → NO + 2H2O.
6. Объединяют найденные выражения и записывают результат: FeS2 + 8H20 + 5NO-3 + 20H+ → Fe3+ + 2SO2−4 + 16H+ + 5NO + 10H2O.

Уравнение можно сократить на 16H + и 8H2O. В итоге получится сокращённое выражение окислительно-восстановительной реакции: FeS2 + 5NO — 3 + 4 H + = Fe3 + + 2SO 2- 4 + 5NO + 2H2O.

Такой алгоритм считается классическим, но для упрощения понимания лучше использовать способ электронного баланса. Процесс восстановления переписывают как N5+ + 3e → N2+. Степень же окисления составить сложнее. Сере нужно приписать степень 2+ и учесть, что на 1 атом железа приходится 2 атома серы: FeS2 → Fe3++ 2S6+. Запись общего баланса будет выглядеть: FeS2 + 5N5+ = Fe3+ + 2S6+ + 5N2+.

Пять молекул потратятся на окисление серного железа, а ещё 3 на образование Fe (NO3)3. После уравнения двух сторон запись реакции примет вид, аналогичный полученному с использованием предыдущего метода.

Использование онлайн-расчёта

Простые уравнения решать самостоятельно довольно просто. Но состоящие из сложных веществ могут вызвать трудности даже у опытных химиков. Чтобы получить точную формулу и не подбирать вручную коэффициенты, можно воспользоваться онлайн-калькуляторами. При этом их использовать сможет даже пользователь, не особо разбирающийся в науке.

Чтобы расстановка коэффициентов в химических уравнениях онлайн происходила автоматически, нужно лишь подключение к интернету и исходные данные. Система самостоятельно вычислит продукты реакции и уравняет обе стороны формулы. Интересной особенностью таких сайтов является не только быстрый и правильный расчёт, но и описание правил с алгоритмами, по которому выполняются действия.

После загрузки калькулятора в веб-обозревателе единственное, что требуется от пользователя — правильно ввести реагенты в специальные формы латинскими буквами и нажать кнопку «Уравнять». Иногда возникает ситуация, когда запись сделана верно, но коэффициенты не расставляются. Это происходит, если суммы в уравнении могут быть подсчитаны разными способами. Характерно это для реакций окисления. В таком случае нужно заменить фрагменты молекул на любой произвольный символ. Таким способом можно не только рассчитать непонятное уравнение, но и выполнить проверку своих вычислений.