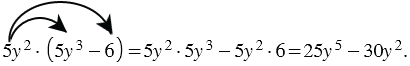Как умножить одночлен на многочлен уравнения

Умножение одночлена на многочлен

Чтобы умножить одночлен на многочлен, надо умножить на этот одночлен каждый член многочлена и полученные произведения сложить.

При умножении одночлена на многочлен используется распределительное свойство умножения:

Произведением одночлена и многочлена будет многочлен.

Пример 1. Умножить одночлен -5a на многочлен 3a + 4b 2 .

Решение: Составим произведение одночлена и многочлена и с помощью распределительного свойства умножения раскроем скобки:

Теперь осталось выполнить умножение одночленов друг на друга:

Так как в получившемся результате нет подобных членов, то многочлен -15a 2 — 20ab 2 — это окончательный результат умножения одночлена -5a на многочлен 3a + 4b 2 .

Пример 2. Выполните умножение многочлена x — xy + 2 на одночлен 2y.

Решение: Составим произведение многочлена и одночлена:

Для удобства можно записать одночлен перед многочленом, используя переместительное свойство умножения. После этого раскроем скобки:

Теперь надо перемножить одночлены:

Решение данного примера можно записать короче, не выписывая промежуточные результаты:

Пример 3. Упростите выражение:

Решение: Раскроем скобки, выполнив умножение —x на 4x — 6y, и затем сделаем приведение подобных членов (если они будут):

Так как получившийся в результате многочлен является алгебраической суммой, то его можно записать так:

Умножение одночлена на многочлен

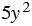
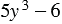
Умножим одночлен на многочлен .

Для этого составим их произведение и, используя распределительное свойство умножения, преобразуем его. Для этого умножим одночлен на каждый член многочлена и сложим результаты:

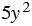
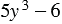
То есть произведение одночлена и многочлена мы представили в виде многочлена .

Вообще, произведение одночлена и многочлена всегда можно представить в виде многочлена. При умножении одночлена на многочлен пользуются правилом:

Приведённое правило позволяет умножать многочлен на одночлен, так как для произведения одночлена и многочлена справедливо переместительное свойство умножения относительно сложения и вычитания.

Поделись с друзьями в социальных сетях:

Умножение многочлена на одночлен: правило, примеры

Частный случай умножения многочлена на многочлен – умножение многочлена на одночлен. В этой статье сформулируем правило совершения этого действия и разберем теорию на практических примерах.

Правило умножения многочлена на одночлен

Разберемся с тем, что является основой умножения многочлена на одночлен. Данное действие опирается на распределительное свойство умножения относительно сложения. Буквенно это свойство записывается так: ( a + b ) · c = a · c + b · c ( a , b и c – некоторые числа). В этой записи выражение ( a + b ) · c является как раз произведением многочлена ( a + b ) на одночлен c . Правая же часть равенства a · c + b · c — это сумма произведений одночленов a и b на одночлен c .

Приведенные рассуждения позволяют нам сформулировать правило умножения многочлена на одночлен:

Для осуществления действия умножения многочлена на одночлен необходимо:

• записать произведение многочлена и одночлена, которые необходимо перемножить;
• умножить каждый член многочлена на заданный одночлен;
• найти сумму полученных произведений.

Дополнительно поясним приведенный алгоритм.

Чтобы составить произведение многочлена на одночлен, исходный многочлен заключают в скобки; далее между ним и заданным одночленом ставится знак умножения. В случае, когда запись одночлена начинается со знака минус, его также необходимо заключить в скобки. К примеру, произведение многочлена − 4 · x 2 + x − 2 и одночлена 7 · y запишем как ( − 4 · x 2 + x − 2 ) · 7 · y , а произведение многочлена a 5 · b − 6 · a · b и одночлена − 3 · a 2 составим в виде: ( a 5 · b − 6 · a · b ) · ( − 3 · a 2 ) .

Следующий шаг алгоритма – перемножение каждого члена многочлена на заданный одночлен. Составляющими многочлена служат одночлены, т.е. по сути нам необходимо выполнить умножение одночлена на одночлен. Допустим, что после первого шага алгоритма мы получили выражение ( 2 · x 2 + x + 3 ) · 5 · x , тогда вторым шагом перемножаем каждый член многочлена 2 · x 2 + x + 3 с одночленом 5 · x , получая таким образом: 2 · x 2 · 5 · x = 10 · x 3 , x · 5 · x = 5 · x 2 и 3 · 5 · x = 15 · x . Результатом станут одночлены 10 · x 3 , 5 · x 2 и 15 · x .

Последнее действие согласно правилу — сложение полученных произведений. Из предложенного примера, проделав данный шаг алгоритма, получим: 10 · x 3 + 5 · x 2 + 15 · x .

Стандартно все шаги записывают как цепочку равенств. Например, нахождение произведения многочлена 2 · x 2 + x + 3 и одночлена 5 · x запишем так: ( 2 · x 2 + x + 3 ) · 5 · x = 2 · x 2 · 5 · x + x · 5 · x + 3 · 5 · x = 10 · x 3 + 5 · x 2 + 15 · x . Исключив промежуточное вычисление второго шага, краткое решение возможно оформить следующим образом: ( 2 · x 2 + x + 3 ) · 5 · x = 10 · x 3 + 5 · x 2 + 15 · x .

Рассмотренные примеры дают возможность заметить важный нюанс: в результате перемножения многочлена и одночлена получается многочлен. Данное утверждение верно для любых перемножаемых многочлена и одночлена.

По аналогии осуществляется умножение одночлена на многочлен: заданный одночлен перемножают с каждым членом многочлена и полученные произведения суммируются.

Примеры умножения многочлена на одночлен

Необходимо найти произведение: 1 , 4 · x 2 — 3 , 5 · y · — 2 7 · x .

Решение

Первый шаг правила уже выполнен – произведение записано. Теперь выполняем следующий шаг, умножая каждый член многочлена на заданный одночлен. В данном случае удобно сначала перевести десятичные дробив обыкновенные. Тогда получим:

1 , 4 · x 2 — 3 , 5 · y · — 2 7 · x = 1 , 4 · x 2 · — 2 7 · x — 3 , 5 · y · — 2 7 · x = = — 1 , 4 · 2 7 · x 2 · x + 3 , 5 · 2 7 · x · y = — 7 5 · 2 7 · x 3 + 7 5 · 2 7 · x · y = — 2 5 · x 3 + x · y

Ответ: 1 , 4 · x 2 — 3 , 5 · y · — 2 7 · x = — 2 5 · x 3 + x · y .

Уточним, что, когда исходные многочлен и/или одночлен заданы в нестандартном виде, перед тем, как найти их произведение, желательно привести их к стандартному виду.

Заданы многочлен 3 + a − 2 · a 2 + 3 · a − 2 и одночлен − 0 , 5 · a · b · ( − 2 ) · a . Необходимо найти их произведение.

Решение

Мы видим, что исходные данные представлены в нестандартном виде, поэтому для удобства дальнейших вычислений приведем их в стандартный вид:

− 0 , 5 · a · b · ( − 2 ) · a = ( − 0 , 5 ) · ( − 2 ) · ( a · a ) · b = 1 · a 2 · b = a 2 · b 3 + a − 2 · a 2 + 3 · a − 2 = ( 3 − 2 ) + ( a + 3 · a ) − 2 · a 2 = 1 + 4 · a − 2 · a 2

Теперь осуществим перемножение одночлена a 2 · b на каждый член многочлена 1 + 4 · a − 2 · a 2

a 2 · b · ( 1 + 4 · a − 2 · a 2 ) = a 2 · b · 1 + a 2 · b · 4 · a + a 2 · b · ( − 2 · a 2 ) = = a 2 · b + 4 · a 3 · b − 2 · a 4 · b

Мы могли бы не приводить исходные данные к стандартному виду: решение при этом оказалось бы более громоздким. При этом последним шагом возникал бы необходимость приведения подобных членов. Для понимания приведем решение по этой схеме:

− 0 , 5 · a · b · ( − 2 ) · a · ( 3 + a − 2 · a 2 + 3 · a − 2 ) = = − 0 , 5 · a · b · ( − 2 ) · a · 3 − 0 , 5 · a · b · ( − 2 ) · a · a − 0 , 5 · a · · b · ( − 2 ) · a · ( − 2 · a 2 ) − 0 , 5 · a · b · ( − 2 ) · a · 3 · a − 0 , 5 · a · b · ( − 2 ) · a · ( − 2 ) = = 3 · a 2 · b + a 3 · b − 2 · a 4 · b + 3 · a 3 · b − 2 · a 2 · b = a 2 · b + 4 · a 3 · b − 2 · a 4 · b

Ответ: − 0 , 5 · a · b · ( − 2 ) · a · ( 3 + a − 2 · a 2 + 3 · a − 2 ) = a 2 · b + 4 · a 3 · b − 2 · a 4 · b .