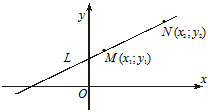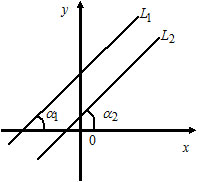Уравнение прямой
Уравнение прямой на плоскости
Любую прямую на плоскости можно задать уравнением прямой первой степени вида
где A и B не могут быть одновременно равны нулю.
Уравнение прямой с угловым коэффициентом
Общее уравнение прямой при B≠0 можно привести к виду
где k — угловой коэффициент равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ.
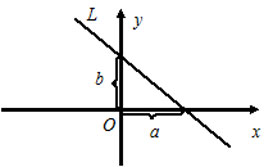
Уравнение прямой в отрезках на осях
Если прямая пересекает оси OX и OY в точках с координатами ( a , 0) и (0, b ), то она может быть найдена используя формулу уравнения прямой в отрезках
| x | + | y | = 1 |
| a | b |
Уравнение прямой, проходящей через две различные точки на плоскости
Если прямая проходит через две точки M( x 1, y 1) и N( x 2, y 2), такие что x 1 ≠ x 2 и y 1 ≠ y 2, то уравнение прямой можно найти, используя следующую формулу
| x — x 1 | = | y — y 1 |
| x 2 — x 1 | y 2 — y 1 |
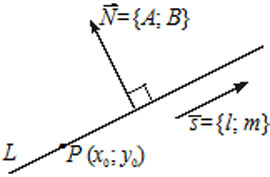
Параметрическое уравнение прямой на плоскости
Параметрические уравнения прямой могут быть записаны следующим образом
x = l t + x 0 y = m t + y 0
где N( x 0, y 0) — координаты точки лежащей на прямой, a = < l , m >— координаты направляющего вектора прямой.
Каноническое уравнение прямой на плоскости
Если известны координаты точки N( x 0, y 0) лежащей на прямой и направляющего вектора a =
| x — x 0 | = | y — y 0 |
| l | m |
Решение. Воспользуемся формулой для уравнения прямой проходящей через две точки
x — 1 2 — 1 = y — 7 3 — 7
Упростив это уравнение получим каноническое уравнение прямой
Выразим y через x и получим уравнение прямой с угловым коэффициентом
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
x = t + 1 y = -4 t + 7
Решение. Так как M y — N y = 0, то невозможно записать уравнение прямой проходящей через две точки.
Найдем параметрическое уравнение прямой. В качестве направляющего вектора можно взять вектор MN .
Взяв в качестве координат точки лежащей на прямой, координаты точки М, запишем параметрическое уравнение прямой
Уравнение прямой в пространстве
Уравнение прямой, проходящей через две различные точки в пространстве
Если прямая проходит через две точки M( x 1, y 1, z 1) и N( x 2, y 2, z 2), такие что x 1 ≠ x 2, y 1 ≠ y 2 и z 1 ≠ z 2, то уравнение прямой можно найти используя следующую формулу
| x — x 1 | = | y — y 1 | = | z — z 1 |
| x 2 — x 1 | y 2 — y 1 | z 2 — z 1 |
Параметрическое уравнение прямой в пространстве
Параметрические уравнения прямой могут быть записаны следующим образом
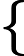 | x = l t + x 0 |
| y = m t + y 0 | |
| z = n t + z 0 |
где ( x 0, y 0, z 0) — координаты точки лежащей на прямой,
Каноническое уравнение прямой в пространстве
Если известны координаты точки M( x 0, y 0, z 0) лежащей на прямой и направляющего вектора n =
| x — x 0 | = | y — y 0 | = | z — z 0 |
| l | m | n |
Прямая как линия пересечения двух плоскостей
Если прямая является пересечением двух плоскостей, то ее уравнение можно задать следующей системой уравнений
Общее уравнение прямой: описание, примеры, решение задач
Данная статья продолжает тему уравнения прямой на плоскости: рассмотрим такой вид уравнения, как общее уравнение прямой. Зададим теорему и приведем ее доказательство; разберемся, что такое неполное общее уравнение прямой и как осуществлять переходы от общего уравнения к другим типам уравнений прямой. Всю теорию закрепим иллюстрациями и решением практических задач.
Общее уравнение прямой: основные сведения
Пусть на плоскости задана прямоугольная система координат O x y .
Любое уравнение первой степени, имеющее вид A x + B y + C = 0 , где А , В , С – некоторые действительные числа ( А и В не равны одновременно нулю) определяет прямую линию в прямоугольной системе координат на плоскости. В свою очередь, любая прямая в прямоугольной системе координат на плоскости определяется уравнением, имеющим вид A x + B y + C = 0 при некотором наборе значений А , В , С .
указанная теорема состоит из двух пунктов, докажем каждый из них.
- Докажем, что уравнение A x + B y + C = 0 определяет на плоскости прямую.
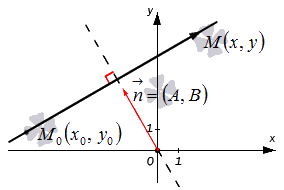
Пусть существует некоторая точка М 0 ( x 0 , y 0 ) , координаты которой отвечают уравнению A x + B y + C = 0 . Таким образом: A x 0 + B y 0 + C = 0 . Вычтем из левой и правой частей уравнений A x + B y + C = 0 левую и правую части уравнения A x 0 + B y 0 + C = 0 , получим новое уравнение, имеющее вид A ( x — x 0 ) + B ( y — y 0 ) = 0 . Оно эквивалентно A x + B y + C = 0 .
Полученное уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 является необходимым и достаточным условием перпендикулярности векторов n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) . Таким образом, множество точек M ( x , y ) задает в прямоугольной системе координат прямую линию, перпендикулярную направлению вектора n → = ( A , B ) . Можем предположить, что это не так, но тогда бы векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) не являлись бы перпендикулярными, и равенство A ( x — x 0 ) + B ( y — y 0 ) = 0 не было бы верным.
Следовательно, уравнение A ( x — x 0 ) + B ( y — y 0 ) = 0 определяет некоторую прямую в прямоугольной системе координат на плоскости, а значит и эквивалентное ему уравнение A x + B y + C = 0 определяет ту же прямую. Так мы доказали первую часть теоремы.
- Приведем доказательство, что любую прямую в прямоугольной системе координат на плоскости можно задать уравнением первой степени A x + B y + C = 0 .
Зададим в прямоугольной системе координат на плоскости прямую a ; точку M 0 ( x 0 , y 0 ) , через которую проходит эта прямая, а также нормальный вектор этой прямой n → = ( A , B ) .
Пусть также существует некоторая точка M ( x , y ) – плавающая точка прямой. В таком случае, векторы n → = ( A , B ) и M 0 M → = ( x — x 0 , y — y 0 ) являются перпендикулярными друг другу, и их скалярное произведение есть нуль:
n → , M 0 M → = A ( x — x 0 ) + B ( y — y 0 ) = 0
Перепишем уравнение A x + B y — A x 0 — B y 0 = 0 , определим C : C = — A x 0 — B y 0 и в конечном результате получим уравнение A x + B y + C = 0 .
Так, мы доказали и вторую часть теоремы, и доказали всю теорему в целом.
Уравнение, имеющее вид A x + B y + C = 0 – это общее уравнение прямой на плоскости в прямоугольной системе координат O x y .
Опираясь на доказанную теорему, мы можем сделать вывод, что заданные на плоскости в фиксированной прямоугольной системе координат прямая линия и ее общее уравнение неразрывно связаны. Иначе говоря, исходной прямой соответствует ее общее уравнение; общему уравнению прямой соответствует заданная прямая.
Из доказательства теоремы также следует, что коэффициенты А и В при переменных x и y являются координатами нормального вектора прямой, которая задана общим уравнением прямой A x + B y + C = 0 .
Рассмотрим конкретный пример общего уравнения прямой.
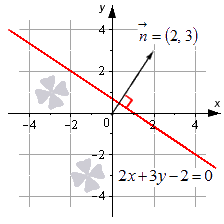
Пусть задано уравнение 2 x + 3 y — 2 = 0 , которому соответствует прямая линия в заданной прямоугольной системе координат. Нормальный вектор этой прямой – это вектор n → = ( 2 , 3 ) . Изобразим заданную прямую линию на чертеже.
Также можно утверждать и следующее: прямая, которую мы видим на чертеже, определяется общим уравнением 2 x + 3 y — 2 = 0 , поскольку координаты всех точек заданной прямой отвечают этому уравнению.
Мы можем получить уравнение λ · A x + λ · B y + λ · C = 0 , умножив обе части общего уравнения прямой на число λ , не равное нулю. Полученное уравнение является эквивалентом исходного общего уравнения, следовательно, будет описывать ту же прямую на плоскости.
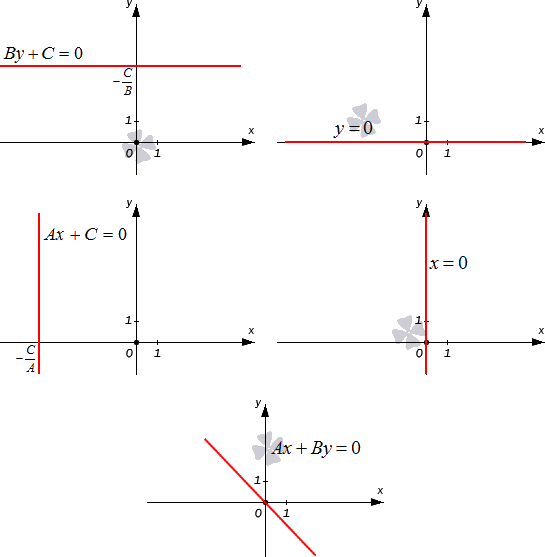
Неполное уравнение общей прямой
Полное общее уравнение прямой – такое общее уравнение прямой A x + B y + C = 0 , в котором числа А , В , С отличны от нуля. В ином случае уравнение является неполным.
Разберем все вариации неполного общего уравнения прямой.
- Когда А = 0 , В ≠ 0 , С ≠ 0 , общее уравнение принимает вид B y + C = 0 . Такое неполное общее уравнение задает в прямоугольной системе координат O x y прямую, которая параллельна оси O x , поскольку при любом действительном значении x переменная y примет значение — C B . Иначе говоря, общее уравнение прямой A x + B y + C = 0 , когда А = 0 , В ≠ 0 , задает геометрическое место точек ( x , y ) , координаты которых равны одному и тому же числу — C B .
- Если А = 0 , В ≠ 0 , С = 0 , общее уравнение принимает вид y = 0 . Такое неполное уравнение определяет ось абсцисс O x .
- Когда А ≠ 0 , В = 0 , С ≠ 0 , получаем неполное общее уравнение A x + С = 0 , задающее прямую, параллельную оси ординат.
- Пусть А ≠ 0 , В = 0 , С = 0 , тогда неполное общее уравнение примет вид x = 0 , и это есть уравнение координатной прямой O y .
- Наконец, при А ≠ 0 , В ≠ 0 , С = 0 , неполное общее уравнение принимает вид A x + B y = 0 . И это уравнение описывает прямую, которая проходит через начало координат. В самом деле, пара чисел ( 0 , 0 ) отвечает равенству A x + B y = 0 , поскольку А · 0 + В · 0 = 0 .
Графически проиллюстрируем все вышеуказанные виды неполного общего уравнения прямой.
Известно, что заданная прямая параллельна оси ординат и проходит через точку 2 7 , — 11 . Необходимо записать общее уравнение заданной прямой.
Решение
Прямая, параллельная оси ординат, задается уравнением вида A x + C = 0 , в котором А ≠ 0 . Также условием заданы координаты точки, через которую проходит прямая, и координаты этой точки отвечают условиям неполного общего уравнения A x + C = 0 , т.е. верно равенство:
Из него возможно определить C , если придать A какое-то ненулевое значение, к примеру, A = 7 . В таком случае получим: 7 · 2 7 + C = 0 ⇔ C = — 2 . Нам известны оба коэффициента A и C , подставим их в уравнение A x + C = 0 и получим требуемое уравнение прямой: 7 x — 2 = 0
Ответ: 7 x — 2 = 0
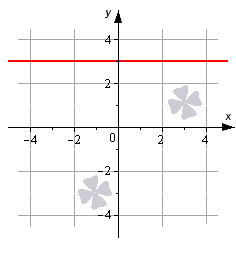
На чертеже изображена прямая, необходимо записать ее уравнение.
Решение
Приведенный чертеж позволяет нам легко взять исходные данные для решения задачи. Мы видим на чертеже, что заданная прямая параллельна оси O x и проходит через точку ( 0 , 3 ) .
Прямую, которая параллельна очи абсцисс, определяет неполное общее уравнение B y + С = 0 . Найдем значения B и C . Координаты точки ( 0 , 3 ) , поскольку через нее проходит заданная прямая, будут удовлетворять уравнению прямой B y + С = 0 , тогда справедливым является равенство: В · 3 + С = 0 . Зададим для В какое-то значение, отличное от нуля. Допустим, В = 1 , в таком случае из равенства В · 3 + С = 0 можем найти С : С = — 3 . Используем известные значения В и С , получаем требуемое уравнение прямой: y — 3 = 0 .
Ответ: y — 3 = 0 .
Общее уравнение прямой, проходящей через заданную точку плоскости
Пусть заданная прямая проходит через точку М 0 ( x 0 , y 0 ) , тогда ее координаты отвечают общему уравнению прямой, т.е. верно равенство: A x 0 + B y 0 + C = 0 . Отнимем левую и правую части этого уравнения от левой и правой части общего полного уравнения прямой. Получим: A ( x — x 0 ) + B ( y — y 0 ) + C = 0 , это уравнение эквивалентно исходному общему, проходит через точку М 0 ( x 0 , y 0 ) и имеет нормальный вектор n → = ( A , B ) .
Результат, который мы получили, дает возможность записывать общее уравнение прямой при известных координатах нормального вектора прямой и координатах некой точки этой прямой.
Даны точка М 0 ( — 3 , 4 ) , через которую проходит прямая, и нормальный вектор этой прямой n → = ( 1 , — 2 ) . Необходимо записать уравнение заданной прямой.
Решение
Исходные условия позволяют нам получить необходимые данные для составления уравнения: А = 1 , В = — 2 , x 0 = — 3 , y 0 = 4 . Тогда:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 1 · ( x — ( — 3 ) ) — 2 · y ( y — 4 ) = 0 ⇔ ⇔ x — 2 y + 22 = 0
Задачу можно было решить иначе. Общее уравнение прямой имеет вид A x + B y + C = 0 . Заданный нормальный вектор позволяет получить значения коэффициентов A и B , тогда:
A x + B y + C = 0 ⇔ 1 · x — 2 · y + C = 0 ⇔ x — 2 · y + C = 0
Теперь найдем значение С, используя заданную условием задачи точку М 0 ( — 3 , 4 ) , через которую проходит прямая. Координаты этой точки отвечают уравнению x — 2 · y + C = 0 , т.е. — 3 — 2 · 4 + С = 0 . Отсюда С = 11 . Требуемое уравнение прямой принимает вид: x — 2 · y + 11 = 0 .
Ответ: x — 2 · y + 11 = 0 .
Задана прямая 2 3 x — y — 1 2 = 0 и точка М 0 , лежащая на этой прямой. Известна лишь абсцисса этой точки, и она равна — 3 . Необходимо определить ординату заданной точки.
Решение
Зададим обозначение координат точки М 0 как x 0 и y 0 . В исходных данных указано, что x 0 = — 3 . Поскольку точка принадлежит заданной прямой, значит ее координаты отвечают общему уравнению этой прямой. Тогда верным будет равенство:
2 3 x 0 — y 0 — 1 2 = 0
Определяем y 0 : 2 3 · ( — 3 ) — y 0 — 1 2 = 0 ⇔ — 5 2 — y 0 = 0 ⇔ y 0 = — 5 2
Ответ: — 5 2
Переход от общего уравнения прямой к прочим видам уравнений прямой и обратно
Как мы знаем, существует несколько видов уравнения одной и той же прямой на плоскости. Выбор вида уравнения зависит от условий задачи; возможно выбирать тот, который более удобен для ее решения. Здесь очень пригодится навык преобразования уравнения одного вида в уравнение другого вида.
Для начала рассмотрим переход от общего уравнения вида A x + B y + C = 0 к каноническому уравнению x — x 1 a x = y — y 1 a y .
Если А ≠ 0 , тогда переносим слагаемое B y в правую часть общего уравнения. В левой части выносим A за скобки. В итоге получаем: A x + C A = — B y .
Это равенство возможно записать как пропорцию: x + C A — B = y A .
В случае, если В ≠ 0 , оставляем в левой части общегь уравнения только слагаемое A x , прочие переносим в правую часть, получаем: A x = — B y — C . Выносим – В за скобки, тогда: A x = — B y + C B .
Перепишем равенство в виде пропорции: x — B = y + C B A .
Конечно, заучивать полученные формулы нет необходимости. Достаточно знать алгоритм действий при переходе от общего уравнения к каноническому.
Задано общее уравнение прямой 3 y — 4 = 0 . Необходимо преобразовать его в каноническое уравнение.
Решение
Запишем исходное уравнение как 3 y — 4 = 0 . Далее действуем по алгоритму: в левой части остаётся слагаемое 0 x ; а в правой части выносим — 3 за скобки; получаем: 0 x = — 3 y — 4 3 .
Запишем полученное равенство как пропорцию: x — 3 = y — 4 3 0 . Так, мы получили уравнение канонического вида.
Ответ: x — 3 = y — 4 3 0 .
Чтобы преобразовать общее уравнение прямой в параметрические, сначала осуществляют переход к каноническому виду, а затем переход от канонического уравнения прямой к параметрическим уравнениям.
Прямая задана уравнением 2 x — 5 y — 1 = 0 . Запишите параметрические уравнения этой прямой.
Решение
Осуществим переход от общего уравнения к каноническому:
2 x — 5 y — 1 = 0 ⇔ 2 x = 5 y + 1 ⇔ 2 x = 5 y + 1 5 ⇔ x 5 = y + 1 5 2
Теперь примем обе части полученного канонического уравнения равными λ , тогда:
x 5 = λ y + 1 5 2 = λ ⇔ x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Ответ: x = 5 · λ y = — 1 5 + 2 · λ , λ ∈ R
Общее уравнение можно преобразовать в уравнение прямой с угловым коэффициентом y = k · x + b , но только тогда, когда В ≠ 0 . Для перехода в левой части оставляем слагаемое B y , остальные переносятся в правую. Получим: B y = — A x — C . Разделим обе части полученного равенство на B , отличное от нуля: y = — A B x — C B .
Задано общее уравнение прямой: 2 x + 7 y = 0 . Необходимо преобразовать то уравнение в уравнение с угловым коэффициентом.
Решение
Произведем нужные действия по алгоритму:
2 x + 7 y = 0 ⇔ 7 y — 2 x ⇔ y = — 2 7 x
Ответ: y = — 2 7 x .
Из общего уравнения прямой достаточно просто получить уравнение в отрезках вида x a + y b = 1 . Чтобы осуществить такой переход, перенесем число C в правую часть равенства, разделим обе части полученного равенства на – С и, наконец, перенесем в знаменатели коэффициенты при переменных x и y :
A x + B y + C = 0 ⇔ A x + B y = — C ⇔ ⇔ A — C x + B — C y = 1 ⇔ x — C A + y — C B = 1
Необходимо преобразовать общее уравнение прямой x — 7 y + 1 2 = 0 в уравнение прямой в отрезках.
Решение
Перенесем 1 2 в правую часть: x — 7 y + 1 2 = 0 ⇔ x — 7 y = — 1 2 .
Разделим на -1/2 обе части равенства: x — 7 y = — 1 2 ⇔ 1 — 1 2 x — 7 — 1 2 y = 1 .
Преобразуем далее в необходимый вид: 1 — 1 2 x — 7 — 1 2 y = 1 ⇔ x — 1 2 + y 1 14 = 1 .
Ответ: x — 1 2 + y 1 14 = 1 .
В общем, несложно производится и обратный переход: от прочих видов уравнения к общему.
Уравнение прямой в отрезках и уравнение с угловым коэффициентом легко преобразовать в общее, просто собрав все слагаемые в левой части равенства:
x a + y b ⇔ 1 a x + 1 b y — 1 = 0 ⇔ A x + B y + C = 0 y = k x + b ⇔ y — k x — b = 0 ⇔ A x + B y + C = 0
Каноническое уравнение преобразуется к общему по следующей схеме:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x ( y — y 1 ) ⇔ ⇔ a y x — a x y — a y x 1 + a x y 1 = 0 ⇔ A x + B y + C = 0
Для перехода от параметрических сначала осуществляется переход к каноническому, а затем – к общему:
x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ A x + B y + C = 0
Заданы параметрические уравнения прямой x = — 1 + 2 · λ y = 4 . Необходимо записать общее уравнение этой прямой.
Решение
Осуществим переход от параметрических уравнений к каноническому:
x = — 1 + 2 · λ y = 4 ⇔ x = — 1 + 2 · λ y = 4 + 0 · λ ⇔ λ = x + 1 2 λ = y — 4 0 ⇔ x + 1 2 = y — 4 0
Перейдем от канонического к общему:
x + 1 2 = y — 4 0 ⇔ 0 · ( x + 1 ) = 2 ( y — 4 ) ⇔ y — 4 = 0
Ответ: y — 4 = 0
Задано уравнение прямой в отрезках x 3 + y 1 2 = 1 . Необходимо осуществить переход к общему виду уравнения.
Решение:
Просто перепишем уравнение в необходимом виде:
x 3 + y 1 2 = 1 ⇔ 1 3 x + 2 y — 1 = 0
Ответ: 1 3 x + 2 y — 1 = 0 .
Составление общего уравнения прямой
Выше мы говорили о том, что общее уравнение возможно записать при известных координатах нормального вектора и координатах точки, через которую проходит прямая. Такая прямая определяется уравнением A ( x — x 0 ) + B ( y — y 0 ) = 0 . Там же мы разобрали соответствующий пример.
Сейчас рассмотрим более сложные примеры, в которых для начала необходимо определить координаты нормального вектора.
Задана прямая, параллельная прямой 2 x — 3 y + 3 3 = 0 . Также известна точка M 0 ( 4 , 1 ) , через которую проходит заданная прямая. Необходимо записать уравнение заданной прямой.
Решение
Исходные условия говорят нам о том, что прямые параллельны, тогда, как нормальный вектор прямой, уравнение которой требуется записать, возьмем направляющий вектор прямой n → = ( 2 , — 3 ) : 2 x — 3 y + 3 3 = 0 . Теперь нам известны все необходимые данные, чтобы составить общее уравнение прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 2 ( x — 4 ) — 3 ( y — 1 ) = 0 ⇔ 2 x — 3 y — 5 = 0
Ответ: 2 x — 3 y — 5 = 0 .
Заданная прямая проходит через начало координат перпендикулярно прямой x — 2 3 = y + 4 5 . Необходимо составить общее уравнение заданной прямой.
Решение
Нормальный вектором заданной прямой будет направляющий вектор прямой x — 2 3 = y + 4 5 .
Тогда n → = ( 3 , 5 ) . Прямая проходит через начало координат, т.е. через точку О ( 0 , 0 ) . Составим общее уравнение заданной прямой:
A ( x — x 0 ) + B ( y — y 0 ) = 0 ⇔ 3 ( x — 0 ) + 5 ( y — 0 ) = 0 ⇔ 3 x + 5 y = 0
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Векторная алгебра
- Высшая математика.
- Аналитическая геометрия.
Аналитическая геометрия.
Прямая на плоскости, всевозможные уравнения.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Существуют такие формы записи уравнения прямой:
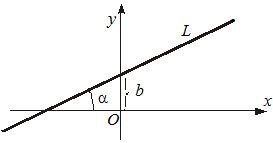
1) $y=kx+b,$ где $k -$ угловой коэффициент, $b-$ отрезок, который прямая отсекает на оси $OY.$
2) $y-y_0=k(x-x_0) $ — уравнение прямой, которая проходит через заданную точку $P(x_0, y_0)$ под заданным углом $\alpha$ к оси $OX$ $(k=tg\alpha).$
3) $\frac
5) $\frac=(l, m) -$ направляющий вектор прямой, то есть вектор параллельный прямой $(\overline\parallel L),$ точка $P(x_0, y_0)\in L.$
6) $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline
7) $Ax+By+C=0 -$ общее уравнение прямой $L,$ где $\overline
8) $x\cos\alpha+y\cos\beta-p=0 -$ нормальное уравнение прямой, где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac
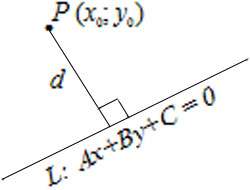
Расстояние от точки $P(x_0, y_0)$ до прямой $L: Ax+By+C=0$ вычисляется по формуле $$d=\left|\frac
Расположение двух прямых на плоскости.
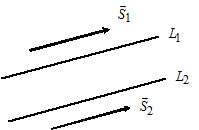
Условия параллельности двух прямых:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$
$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $k_1=k_2.$
2) Пусть $L_1:$ $\frac_1=(l_1, m_1);$
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline_1\parallel\overline_2\Leftrightarrow$ $\frac
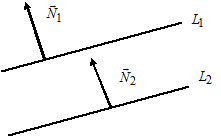
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline
$L_2: A_2x+B_2y+C_2=0,$ $\overline
Прямые $L_1$ и $L_2$ параллельны тогда и только тогда, когда $\overline
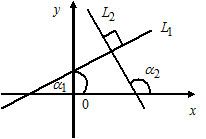
Условия перпендикулярности двух прямых:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$
$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$
$L_1\perp L_2\Leftrightarrow$ $k_1\cdot k_2=-1.$
2) Пусть $L_1:$ $\frac_1=(l_1, m_1);$
$L_1\perp L_2\Leftrightarrow$ $\overline_1\perp\overline_2\Leftrightarrow$ $
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline
$L_2: A_2x+B_2y+C_2=0,$ $\overline
$L_1\perp L_2\Leftrightarrow$ $\overline
Угол между прямыми:
1) Пусть $L_1: k_1x+b_1,$ $k_1=tg\alpha_1;$
$L_2: k_2x+b_2,$ $k_2=tg\alpha_2.$
2) Пусть $L_1:$ $\frac_1=(l_1, m_1);$
3) Пусть $L_1: A_1x+B_1y+C_1=0,$ $\overline
$L_2: A_2x+B_2y+C_2=0,$ $\overline
Примеры:
2.141.
а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и нормальным вектором $\overline N(2; 2).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 6) для уравнения прямых ( $A(x-x_0)+B(y-y_0)=0$ ) соответственно координаты точки $(x_0; y_0)=M_0(-1; 2)$ и вектора $(A; B)=\overline N(2; 2):$
$2(x+1)+2(y-2)=0.$ Далее, приведем это уравнение к общему виду:
Нормальное уравнение прямой имеет вид $x\cos\alpha+y\cos\beta-p=0,$ где $\cos\alpha$ и $\cos\beta -$ направляющие косинусы нормального вектора $n,$ направленного из начала координат в сторону прямой, а $p>0 -$ расстояние от начала координат до прямой.
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac
Для нашей прямой имеем $A=1; B=1; C=-1 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac<-1><\sqrt<1+1>>=\frac<1><\sqrt 2>.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=\frac<1><\sqrt 2>.$
Ответ: $2(x+1)+2(y-2)=0;$ общее уравнение $x+y-1=0;$ нормальное уравнение прямой $\frac<1><\sqrt 2>x+\frac<1><\sqrt 2>y-\frac<1><\sqrt 2>=0;$ $p=\frac<1><\sqrt 2>.$
2.142.
а) Прямая $L$ задана точкой $M_0(-1; 2)\in L$ и направляющим вектором $\overline S(3; -1).$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 5) для уравнения прямых ( $\frac
Далее, приведем это уравнение к общему виду:
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac
Для нашей прямой имеем $A=1; B=3; C=-5 \Rightarrow sgn C=-1.$ Таким образом, $\mu=-\frac<-1><\sqrt<1+9>>=\frac<1><\sqrt<10>>.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=\frac<5><\sqrt <10>>.$
Ответ: $\frac
2.143.
а) Прямая $L$ задана двумя своими точками $M_1(1; 2)\in L$ и $M_2(-1; 0)\in L.$ Требуется: 1) написать уравнение прямой, привести его к общему виду и построить прямую; 2) привести общее уравнение к нормальному виду и указать расстояние от начала координат до прямой.
Решение.
Подставим в формулу 3) для уравнения прямых ($\frac
Далее, приведем это уравнение к общему виду:
Общее уравнение прямой приводится к нормальному, путем умножения на нормирующий множитель $\mu=-\frac
Для нашей прямой имеем $A=1; B=-1; C=1 \Rightarrow sgn C=1.$ Таким образом, $\mu=-\frac<1><\sqrt<1+1>>=-\frac<1><\sqrt<2>>.$
Запишем нормальное уравнение прямой:
Расстояние от начала координат $p=\frac<1><\sqrt <2>>.$
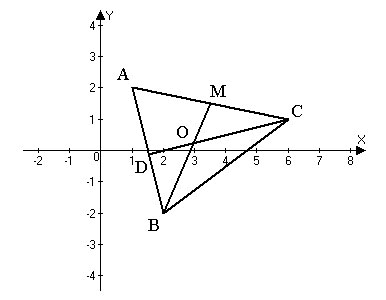
2.150. Треугольник $ABC$ задан координатами своих вершин $A(1; 2), B(2; -2), C(6; 1).$ Требуется:
1) Найти уравнение стороны $AB;$
2) найти уравнение высоты $CD$ и вычислить ее длину $h=|CD|;$
3) найти угол между высотой $CD$ и медианой $BM.$
Решение.
1) Уравнение прямой $AB$ найдем по формуле уравнения прямой, проходящей через две точки $\frac
В нашем случае $(x_1; y_1)=A(1; 2);$ $(x_2; y_2)=B(2; -2).$
Подставляем координаты точек в уравнение прямой. Получаем $$\frac
$-4(x-1)=y-2\Rightarrow$ $-4x+4=y-2\Rightarrow$ $4x+y-6=0.$
2) Уравнение прямой $CD$ найдем, пользуясь уравнением ( 6): $A(x-x_0)+B(y-y_0)=0$ — уравнение прямой $L,$ которая проходит через точку $M(x_0, y_0)$ перпендикулярно вектору $\overline
В нашем случае, высота $CD$ это прямая, которая проходит через точку $C$ перпендикулярно вектору $AB.$
Таким образом, $$(x_0; y_0)=C=(6; 1);\quad\overline
Подставляем эти координаты в уравнение прямой:
$1(x-6)-4(y-1)=0\Rightarrow x-6-4y+4=0 \Rightarrow x-4y-2=0.$
То есть, уравнение прямой $CD:$ $x-4y-2=0.$
Чтобы найти длину высоты $h=|CD|,$ найдем координаты точки $D,$ как точки пересечения прямых $CD$ и $AB:$
Решим систему методом исключений:
Следовательно имеем $D(26/17; -2/17).$ Теперь можем найти длину высоты $CD:$
3) Уравнение высоты $CD$ мы уже нашли в пункте 2). Найдем уравнение медианы $BM.$ Будем его искать, используя форумулу уравнения прямой, проходящей через две точки.
Координаты точки $B=(2, -2); $ координаты точки $M$ найдем как середину стороны $AC:$ $x_M=\frac
Подставляем координаты точек $B(2; -2)$ и $M(3.5; 1.5)$ в уравнение прямой
$3.5(x-2)=1.5(y+2)\Rightarrow 3.5x-7=1.5y+3 \Rightarrow 3.5x-1.5y-10=0.$
Далее, зная общие уравнения двух прямых $CD: x-4y-2=0$ и $BM: 3.5x-1.5y-10=0$ можно найти угол между ними по формуле
где $L_1: A_1x+B_1y+C_1=0,$ $\overline
$L_2: A_2x+B_2y+C_2=0,$ $\overline
Для наших прямых имеем: $(A_1, B_1)=(1; -4);$ $(A_2; B_2)=(3.5; -1.5).$
Ответ: 1) $AB: 4x+y-6=0.$
2.160. В равнобедренном треугольнике $ABC$ заданы вершина $C(4; 3),$ уравнение $2x-y-5=0$ основания $AC$ и уравнение $x-y=0$ боковой стороны $AB.$ Найти уравнение стороны $BC.$
Решение.
Найдем координаты вершины треугольника $A,$ как точки пересечения прямых $AB$ и $AC:$
Таким образом, мы имеем координаты вершин при основании равнобедренного треугольника $A(5; 5)$ и $C(4; 3).$ Найдем координаты вершины $B(x, y).$ Мы знаем, что эта точка принадлежит прямой $AB: x-y=0$ и что $AB=BC.$ Запишем формулы для длин сторон $AB$ и $BC:$
Далее, чтобы найти координаты точки $B,$ решим систему уравнений:
$$\Rightarrow\left\<\begin
Зная координаты точек $B$ и $C$ можно записать уравнение прямой $BC,$ как прямой проходящей через две точки $\left(\frac
$$\Rightarrow\frac
Ответ: $7x-y-25=0.$
2.165. Даны две противоположные вершины квадрата $A(1; 3)$ и $C(-1; 1).$ Найти координаты двух его других вершин и написать уравнения его сторон.
Решение:
Найдем уравнение диагонали $AC:$
Далее, найдем уравнение второй диагонали квадрата — прямой, проходящей через точку $O$ перпендикулярно прямой $AC.$ Для прямой $AC$ нормальный вектор имеет координаты $\overline
$$\frac
Ясно, что $AO=CO=BO=DO.$ Найдем длину отрезка $AO:$ $AO=\sqrt<(0-1)^2+(2-3)^2>=\sqrt<2>.$
Далее, будем искать координаты точек $B$ и $D,$ принадлежащих прямой $BD$ и таких, что $BO=DO=AO.$
Таким образом, мы нашли координаты вершин $B(1; 1)$ и $D(-1; 3).$ Зная координаты вершин квадрата, запишем уравнения его сторон, пользуясь формулой ( 3) — $\frac
Ответ: $A(1; 3),$ $B(1; 1),$ $C(-1; 1),$ $D(-1; 3);$ $AB:$ $x=1;$ $BC:$ $y=1;$ $CD:$ $x=-1;$ $DA:$ $y=3.$
Деление отрезка в заданном отношении (векторный и координатный способы).
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $\lambda,$ в котором точка $M$ делит направленный отрезок $\overline
Пусть $O -$ начало координат. Обозначим $\overline
Примеры.
2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.
Решение.
Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$\lambda_1=\frac
Далее находим координаты точки $D:$
Ответ: $(4, 0)$ и $(5, 2).$
2.58. Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.
Решение.
Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.
Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:
Аналогичные равенства запишем для точки $D:$
Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:
Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$
Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$
Взаимное расположение плоскостей, угол между плоскостями.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Условие параллельности двух плоскостей:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $\overline
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $\overline
Плоскости $P_1$ и $P_2$ параллельны тогда и только тогда, когда $\overline
Условия перпендикулярности двух плоскостей:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $\overline
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $\overline
$P_1\perp P_2\Leftrightarrow$ $\overline
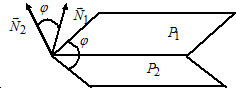
Угол между плоскостями:
Пусть $P_1: A_1x+B_1y+C_1z+D_1=0,$ $\overline
$P_2: A_2x+B_2y+C_2z+D_2=0,$ $\overline
Примеры.
В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1\parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.
2.185. $P_1: -x+2y-z+1=0;$ $P_2: y+3z-1=0.$
Решение.
Вычислим угол между заданными плоскостями.
$P_1: -x+2y-z+1=0, \Rightarrow\overline
$P_2: y+3z-1=0, \Rightarrow\overline
Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями
Ответ: Плоскости пересекаются. $\cos\widehat<(P_1, P_2)>=\frac<1><2\sqrt<15>>.$
Решение.
Вычислим угол между заданными плоскостями.
$P_1: x-y+1=0, \Rightarrow\overline
$P_2: y-z+1=0, \Rightarrow\overline
Соответственно, плоскости пересекаются и косинус кратчайшего угла между плоскостями
Ответ: Плоскости пересекаются. $\cos\widehat<(P_1, P_2)>=\frac<1><2>.$
2.196. Составить уравнение плоскости $P,$ проходящей через точку $A(1, 1, -1)$ и перпендикулярной к плоскостям $P_1: 2x-y+5z+3=0$ и $P_2: x+3y-z-7=0.$
Решение.
Для того, чтобы плоскость $P$ была перпендикулярно плоскостям $P_1$ и $P_2,$ достаточно, чтобы она была параллельна их нормалям $N_1$ и $N_2.$ Или, что тоже самое, перпендикулярна векторному произведению $[N_1, N_2]$
$P_1: 2x-y+5z+3=0, \Rightarrow\overline
$P_2: x+3y-z-7=0, \Rightarrow\overline
Теперь выпишем уравнение плоскости, проходящей через заданную точку $A(1, 1, -1)$ и перпендикулярной вектору $[N_1, N_2]=(-14, 7, 7):$
Ответ: $-2x+y+z+2=0.$
Домашнее задание.
В задачах исследовать взаимное расположение заданных плоскостей. При этом, в случае $P_1\parallel P_2$ то найти расстояние между плоскостями, а в случае — косинус угла между ними.
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/obschee-uravnenie-prjamoj/
http://mathportal.net/index.php/vectoralgebra/87-visshaya-matematika/analiticheskaya-geometriya