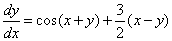Как в matlab simulink моделировать уравнения

Как в matlab simulink моделировать уравнения

Дифференциальные уравнения и системы уравнений

Необходимо решить уравнение:

Попробуем решить его с помощью программы Simulink пакета MATLAB.

Метод решения дифференциальных уравнений отличается от традиционного. Нам необходимо создать схему уравнения. Необходимо будет создать обратную связь между выходными значениями интегратора и новым значением переменной. У нашего уравнения линейно изменяется x от 0 до 20. Поэтому для решения уравнения необходимо использовать блок Ramp . В конце обязательно должен быть интегрирующий блок, а из него результат выходит на осциллограф.

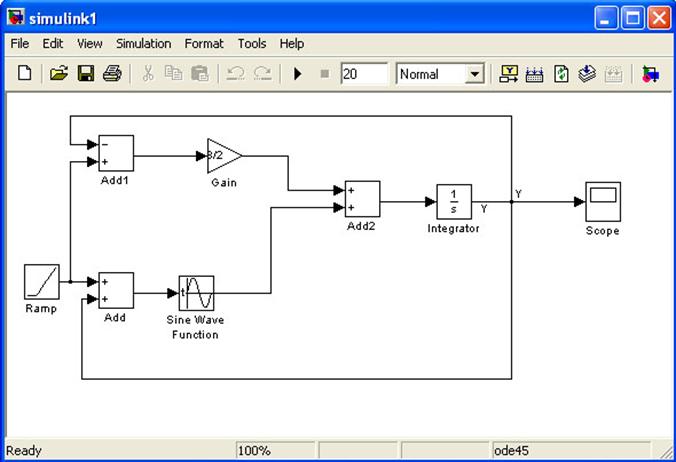
Решение уравнения выглядит так:

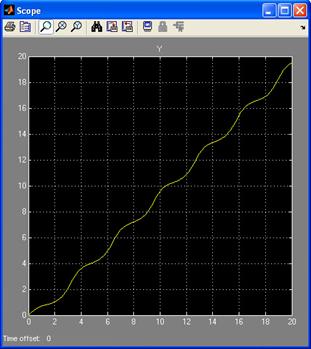
Результатом будет график x от y :

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources. Формирует линейный сигнал . В параметрах необходимо задать 1.

Add – Math Operations. В параметрах выбираем необходимые нам операции.

Gain – Math Operations . Коэффициент усиления сигнала. В параметрах ставим значение 3/2.

Sine Wave Function – Sources. Т.к. нам необходим косинус, то в параметрах Phase ставим pi/2.

Integrator – Continuous . Выполняет интегрирование входного сигнала.

Scope – Sinks . Выводим результат – график сигнала в функции времени.

Дифференциальные уравнения 2-го порядка.

Дана система уравнений:

Решим ее с помощью программы Simulink пакета MATLAB.

Решаем аналогично предыдущему случаю.

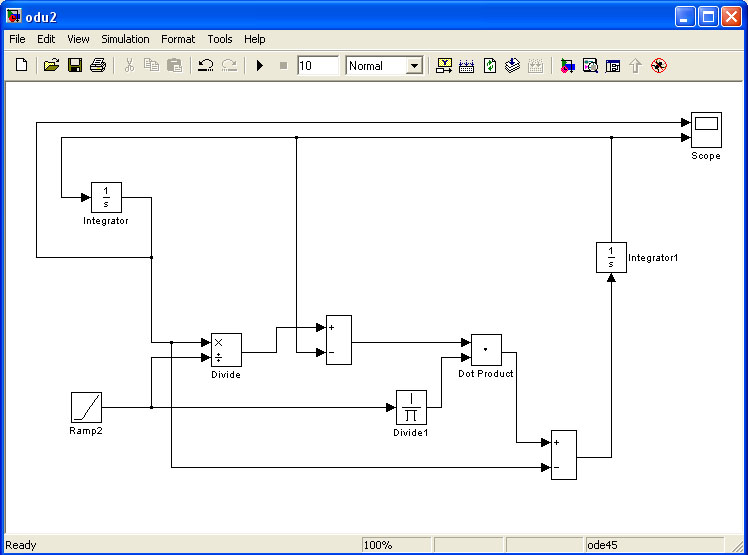
В данной системе уравнений линейно изменяется x от 1 до 10. Также необходимо сделать обратную связь между выходными значениями интеграторов и новым значение переменной x . Обязательно надо в интеграторах задать начальные значения y₁(0) = 0.1; y₂(0) = 0.5.

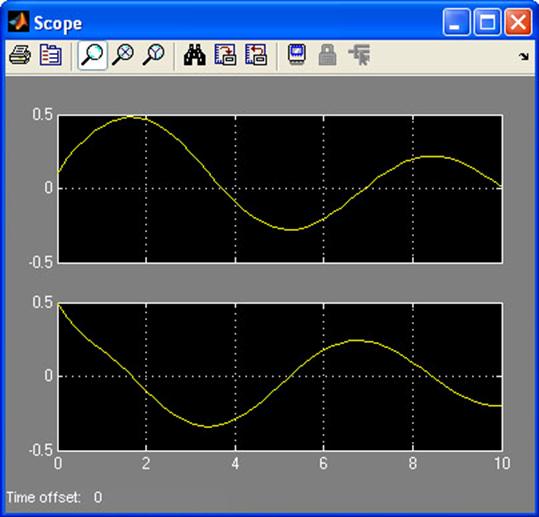
Результатом будут два графика:

Рассмотрим из каких библиотек взяты использованные блоки.

Ramp – из Sources . Формирует линейный сигнал. В параметрах необходимо задать все значения 1.

Integrator – Continuous . Выполняет интегрирование входного сигнала. Необходимо задать начальные значения Initial condition для y ₁ 0.1, для y ₂ 0.5.

Add – Math Operations . В параметрах выбираем необходимые нам операции.

Divide — Math Operations . Деление первой входной величины на вторую.

Dot Product — Math Operations. Перемножение .

Scope – Sinks. Выводим результат – график сигнала в функции времени.

Решение систем обыкновенных дифференциальных уравнений в среде MATLAB. Часть 1

В среде MATLAB можно решать системы диффуров с начальными условиями, краевые задачи, а также решать дифференциальные уравнения в частных производных с помощью инструмента PDE toolbox.

В данном обзоре речь пойдет лишь о системах дифференциальных уравнений с начальными условиями, то есть о задаче Коши. В англоязычной литературе это называется Initial Value Problem.

• каким образом записывать системы диффуров
• как задать начальные условия
• временной интервал
• какой получать результат решения для дальнего использования

Решать системы обыкновенных дифференциальных уравнений можно как в MATLAB, так и в Simulink.

В первую очередь, следует определиться, использовать для решения Matlab и его текстовый редактор, или Simulink, где те же системы дифференциальных уравнений могут быть записаны в виде функциональных блоков.

Выбор ваш должен зависеть от задачи. Если Вы, например, хотите смоделировать какой-либо объект управления, описываемый системой диффуров, то в данном случае имеет смысл использовать именно Simulink, так как Вам, впоследствии, понадобиться синтез, например, системы управления, и Simulink подойдет здесь как нельзя лучше.

А вот если у Вас, например, есть необходимость решать системы диффуров с большим количеством уравнений и неизвестных, или специфика Вашей задачи требует особой и специальной настройки численного метода, а также если вы хотите использовать решение диффура в составе других скриптов MATLAB, то Вам имеет смысл решать дифференциальные уравнения способом, о котором пойдёт речь в этом обзоре.

Рассмотрим синтаксис решателей matlab.В качестве аргументов следует подать правую часть системы в виде MATLAB-функции.

На рисунке показан требуемый вид системы, когда выражены старшие производные.

Системы, чей вид отличается от требуемого, следует преобразовать к таковому.

Если функция простая, то её можно записать прямо в поле аргумента, однако, когда речь идёт о системах уравнений, имеет смысл записывать систему уравнений в виде отдельной функции, в том числе и в виде отдельного м-файла. Об этом мы поговорим чуть позже и на конкретном примере.

Также подается интервал времени, на котором будет найдено решение. Интервал задаётся строкой из двух чисел: начальной величины независимого аргумента t и его конечного значения.

Далее задаются начальные условия. Значения всех неизвестных искомых переменных в начале расчёта задаются в виде столбца соответствующей размерности.

Далее, при необходимости, задаются опции. Вот тут и раскрываются широкие возможности MATLAB по настройке решателя. Помимо управления точностью и величиной шага, имеется возможность обрабатывать данные в процессе вычисления, а также выполнять скрипты по завершению вычисления. Но ещё более полезным является опция отслеживания событий по условию, более подробно поговорим об этом дальше. Также есть другие специальные опции, которые могут быть использованы при решении определённых типов систем.

Вы могли заметить, что название функции — odeXY – это обозначение для всех решателей, которых всего 8 штук. В данном ролике мы пользоваться решателем ode45, соответствующего численному по методу Дормана-Принса 4(5). Этого решателя достаточно для подавляющего большинства задач. Остальные решатели будут подробно рассмотрены в приложении к задачам соответствующих типов позже.

Перейдем к примерам.

Рассмотрим 2 примера:

• решение дифференциального уравнения первого порядка.
• решение системы двух дифференциальных уравнений второго порядка.

В качестве уравнение первого порядка рассмотрим логистическое уравнение Ферхюльста, которое описывает динамику численности популяции. Суть уравнения такова: скорость прироста населения y пропорциональна количеству населения, однако лимитирована максимальной численностью популяции.

Забавный факт: Ферхюльст назвал это уравнение логистическим, и никто до сих пор не знает почему, ибо сам Ферхюльст об этом никому не рассказал.

Решение этого дифференциального уравнения выглядит следующим образом.

Пишем функцию в явном виде, задаём интервал расчёта и записываем начальное условие. Пару слов о записи функции подобным образом. Знак собаки в матлабе является оператором создания функции соответствующих переменных. Вы задаёте аргументы функции и саму функцию через пробел, как показано на рисунке.

Перейдем в окно MATLABа и посмотрим, как это выглядит.

Так выглядит скрипт:

Так выглядит график решения дифференциального уравнения:

В качестве примера решения системы, состоящей из двух дифференциальных уравнений второго порядка, рассмотрим шарик, подвешенный на пружине, который ещё и тормозит о воздух.

Уравнения показаны на рисунке. Но вид системы отличается от требуемого, в том числе потому, что в нём присутствуют вторые производные. Для приведения системы в требуемый вид выполним 2 простых шага:

Первое: следует заменить переменные соответствующим образом. Теперь у нас 4 неизвестных. Далее следует преобразовать уравнение с учетом замены. Таким образом, мы имеем систему из четырёх дифференциальных уравнений первого порядка.

Настало время её записать.

Итак, мы имеем систему, параметры, интервал времени и начальные условия. Решим же эту задачу скорее.

В отличие от предыдущего примера, систему четырех уравнений проблематично записать в поле аргумента. Поэтому всю систему будем записывать в отдельную функцию.

Эту функцию можно располагать как в самом скрипте решения в самом его конце, так и в виде отдельного m-файла.

На выходе функция должна представлять собой вектор-столбец, который записывается перечислением компонент через точку запятой как показано на рисунке.

Теперь рассмотрим скрипт самого решения.

На этот раз запишем интервал и начальные условия в виде переменных MATLAB. Интервал, соответственно, в виде строки, а начальные условия – в виде столбца длинной 4.

Сообразно с уже разобранным ранее синтаксисом укажем функцию pendulum_np, интервал времени и начальные условия.

Перейдем теперь в окно MATLAB и посмотрим решение.

Так выглядит скрипт:

Запускаем скрипт и получаем графики:

Зачастую хочется, чтобы одну и ту же систему можно было бы решать с разными параметрами, и при этом не менять их в теле самой функции. И это можно, и даже нужно осуществлять.

На рисунке показана функция MATLAB, которая соответствует движению подвешенного на пружине шара, однако можно заметить, что эта функция теперь имеет на 5 аргументов больше.

Параметры задаются в скрипте, а при вызове функции мы обращаемся к уже известному оператору-собаке, которая превращает функцию семи переменных pendulum_n в функцию двух переменных t и X. Вот и всё.

Я вам очень рекомендую разобраться с тем, как работает оператор-собака. В хелпе он называется function-handle. Разобравшись с ним Вам будет работать в среде MATLAB ещё проще и ещё приятнее.

Вывод: не так страшно решать диффуры

Под конец стоит сказать какие вообще системы дифференциальных уравнений матлаб может решать, а может он решать системы практически любых типов.

Их можно, с одной стороны, разделить по степени жёсткости, а с другой стороны, по структуре самой системы.

Когда уравнения представляют поведение системы, которая содержит ряд быстрых и медленных реакций, то такую систему уравнения можно назвать жесткой. Для жестких задач явные численные методы работают плохо, или не работают вовсе. Примером жесткой задачи может являться протекание тока через клеточную мембрану. На самом деле, чёткого разделения между жесткими и нежёсткими системами не существует. Степень жесткости системы формально определяется через собственные значения матрицы Якоби, но давайте не будем закапываться.

Видеообзор по теме решения систем Д/У доступен по ссылке.

Моделирование дифференциальных уравнений в среде matlab & Simulink Текст научной статьи по специальности « Математика»

Аннотация научной статьи по математике, автор научной работы — Бадасян Тигран Смбатович

Пакет программ MatLab предназначен для аналитического и численного решения различных математических задач, а также для моделирования сложных электротехнических и электромеханических систем. Одним из инструментальных средств является среда MatLab, которая оснащена мощными возможностями структурного, объектно-ориентированного и визуального программирования (Simulink). Система инженерных и научных расчётов MatLab (Matrix Laboratory матричная лаборатория) способна решать задачи линейной алгебры, интегральные и дифференциальные уравнения, выполнять преобразования Лапласа и Фурье, Z-преобразования. Предусмотрено решение статистических и оптимизационных задач. Благодаря программе Simulink имеется возможность анализа и синтеза современных систем управления во временной и частотной областях. Графические возможности пакета позволяют строить двухи трёхмерные графики в различных координатах. При решении дифференциальных уравнений, в частности, для дифференциальных уравнений в частных производных применять Simulink и инструментарий Partial diferencial Equations Toolbox [3, 4]. Вложенный в него метод конечных элементов (finite elements method FEM) позволяет моделировать решение задачи на плоскости или в пространстве.

Похожие темы научных работ по математике , автор научной работы — Бадасян Тигран Смбатович

MODELING OF DIFFERENTIAL EQUATIONS ENVIRONMENT MATLAB & SIMULINK

The MatLab software package is designed for analytical and numerical solutions of various mathematical problems, as well as for modeling complex electrical and electromechanical systems. One of the tools is the MatLab environment, which is equipped with powerful structural, object-oriented and visual programming (Simulink) capabilities. MatLab (Matrix Laboratory) is capable of solving linear algebra problems, integral and differential equations, performing Laplace and Fourier transforms, and Z-transformations. The solution of statistical and optimization problems is provided. Thanks to the Simulink program, it is possible to analyze and synthesize modern control systems in the time and frequency domains. The graphical capabilities of the package allow you to build two and three-dimensional graphs in different coordinates. When solving differential equations, in particular, for partial differential equations, use Simulink and the Partial diferencial Equations Toolbox [3,4]. The finite element method (FEM) embedded in it allows you to simulate a solution to a problem on a plane or in space.

Текст научной работы на тему «Моделирование дифференциальных уравнений в среде matlab & Simulink»

МОДЕЛИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ В СРЕДЕ

MATLAB & SIMULINK Бадасян Т.С. Email: Badasyan1166@scientifictext.ru

Бадасян Тигран Смбатович — магистрант, факультет прикладной математики и физики, Национальный политехнический университет Армении, г. Ереван, Республика Армения

Аннотация: пакет программ MatLab предназначен для аналитического и численного решения различных математических задач, а также для моделирования сложных электротехнических и электромеханических систем. Одним из инструментальных средств является среда MatLab, которая оснащена мощными возможностями структурного, объектно-ориентированного и визуального программирования (Simulink).

Система инженерных и научных расчётов MatLab (Matrix Laboratory — матричная лаборатория) способна решать задачи линейной алгебры, интегральные и дифференциальные уравнения, выполнять преобразования Лапласа и Фурье, Z-преобразования. Предусмотрено решение статистических и оптимизационных задач. Благодаря программе Simulink имеется возможность анализа и синтеза современных систем управления во временной и частотной областях. Графические возможности пакета позволяют строить двух- и трёхмерные графики в различных координатах. При решении дифференциальных уравнений, в частности, для дифференциальных уравнений в частных производных применять Simulink и инструментарий Partial diferencial Equations Toolbox [3, 4]. Вложенный в него метод конечных элементов (finite elements method FEM) позволяет моделировать решение задачи на плоскости или в пространстве.

Ключевые слова: среда, сигнал, блок интегрирования, линейное уравнение, однородное уравнение.

MODELING OF DIFFERENTIAL EQUATIONS ENVIRONMENT

MATLAB & SIMULINK Badasyan T.S.

Badasyan Tigran Smbatovich — Undergraduate Student, FACULTY OF APPLIED MATHEMATICS AND PHYSICS, NATIONAL POLYTECHNIC UNIVERSITY OF ARMENIA, YEREVAN, REPUBLIC OF ARMENIA

Abstract: the MatLab software package is designed for analytical and numerical solutions of various mathematical problems, as well as for modeling complex electrical and electromechanical systems. One of the tools is the MatLab environment, which is equipped with powerful structural, object-oriented and visual programming (Simulink) capabilities.

MatLab (Matrix Laboratory) is capable of solving linear algebra problems, integral and differential equations, performing Laplace and Fourier transforms, and Z-transformations. The solution of statistical and optimization problems is provided. Thanks to the Simulink program, it is possible to analyze and synthesize modern control systems in the time and frequency domains. The graphical capabilities of the package allow you to build two and three-dimensional graphs in different coordinates. When solving differential equations, in particular, for partial differential equations, use Simulink and the Partial diferencial Equations Toolbox [3,4]. The finite element method (FEM) embedded in it allows you to simulate a solution to a problem on a plane or in space. Keywords: medium, signal, integration unit, linear equation, homogeneous equation.

Введение. Задачи различных отраслей часто сводятся к дифференциальным уравнениям или системам дифференциальных уравнений [1, 2]. Часто возможно бывает решить дифференциальные уравнения аналитически, однако немало случаев, когда уравнение не

имеет точного аналитического решения и возникает необходимость обратиться к численным методам. Разработан ряд численных методов, которыми возможно решить дифференциальные уравнения. Однако ошибочно думать, что решение любого дифференциального уравнения или системы дифференциальных уравнений численными методами — это легкая задача. Причина в том, что нет разработанного численного метода, который позволил бы решить произвольное дифференциальное уравнение. Необходимо иметь четкое представление о том, какой численный метод является более эффективным для решения данного дифференциального уравнения.

Целью статьи является демонстрация возможностей пакета Simulink при компьютерном моделировании дифференциальных уравнений, имитационного моделирования динамических систем. Simulink — один из самых мощных компонентов числового пакета МАТЬАВ, предназначенный для компьютерного моделирования и анализа систем, поведение которых зависит от времени [3, 4].

Моделирование обыкновенных дифференциальных уравнений первого порядка.

Исследование, как правило, начнем с простейшего типа — уравнение вида 4у = f (х) с

дискретными переменными, интегральным уравнением которого будет у = J f (х)4х + у(0) . Удовлетворяя начальному условию у(x0 ) = У0 частное

решение будет представлено в виде у = J f (х)4х + у(0) . В частном случае, если

уравнение имеет вид

то частное решение, удовлетворяющее начальному

условию у(х0 ) = Уо , будет иметь вид у = а(х — х0 ) + у0 , которое является уравнением прямой, проходящей через точку (Хо, Уо) на плоскости Я2. Модель s

уравнения 4У = f (х) будет иметь следующий вид (рис.1):

Рис. 1. Решение дифференциального уравнения: структурная схема в Simulink

Далее рассмотрим линейное дифференциальное уравнение первого порядка вида

= р(х) у + / (х). Модель s задачи будет иметь следующий вид (рис. 2):

Рис. 2. Решение дифференциального уравнения первого порядка: структурная схема в Simulink

Основным конструктивным элементом модели линейного уравнения является блок интегрирования, который посредством обратной связи получает на входе решение уравнения. В блоке Product сигнал y(x) умножается на p(x), результат передается блоку Sum для суммирования с f(x).

Обсудим более подробно этапы создания схемы, используемые блоки содержатся в библиотеках. Ramp (библиотека Sources) дает непрерывный линейный сигнал. Sum (библиотека Math Operations) — в параметрах выбираем нужные действия: сложение или вычитание. Product (библиотека Math Operations) — умножает входящие сигналы. Integrator (библиотека Continuous) — выполняет интегрирование входного сигнала. Scope, Graph (библиотека Sinks) — строит графики сигнала и производного сигнала в зависимости от времени: Graph (библиотека Sinks) — Возвращает фазовый сигнал производной, то есть зависимость значения функции от производной функции в техже точках. В меню Simulation редактора выберем Configuration Parameters. В открывшемся окне выберем Solver и введем следующие параметры. Start Time: 0, Stop Time: 10.0, Type: Variable-step, Solver: ode45 (Dormand-Prince). Для проверки результата возьмем программный код той же задачи в среде Matlab, с применением функции dsolve. Очевидно, что в обоих случаях графики совпадут. syms x y

Exp = ‘2*x/(1+xA2)*y+1+xA2’; % определение правой части уравнения Expression = [‘Dy = ‘,char(Exp)];

y = dsolve(Expression,’y(0)=0′,’x’); % решение дифференциальногоуравнения Message = [‘y = ‘,char(y)]; pretty(y); % выводит решение уравнения grid on; hold on; % строит сетку

xlabel(‘X axis’); ylabel(‘Y axis’); % разместить наименование осей x и y x_new = 0:0.1:10; % получает вектор x_new

Cx = symvar(y,1) % функция возвращает количество

y_new = subs(y,,); % создается новый вектор y_new plot(x_new,y_new); Title = [‘Itegral Curves of Equation: ‘,char(Expression)]; title(Title); % название графика

legend(Message); % таблица ссылок графика

Более детально рассмотрим такой мощный инструмент, как механизм сокрытия подсистемы. Механизм сокрытия подсистем позволяет спроектировать подсистему как единный блок, которое хранится в библиотеке, то есть ему можно добавить окно параметров, объекты и справочную систему.

Чтобы скрыть существующую подсистему, нужно сначала выполнить следующие шаги:

■ определить, какие параметры подсистемы использовать в окне будущих пераметров. Определить те параметры, которые надо использовать в подсистеме (Greate subsysten from selection),

■ установить параметр в диалоговом окне,

■ разработать визуализацию блоков,

■ создать комментарии по использованию подсистемы.

Скрытие подсистемы осуществляется посредством редактора Mask Editor. Чтобы запустить редактор скрытия, выберите подсистему скрытия из контекстного меню Diagram, выбрать команду Mask или правой кнопкой мыши открыть окно Explore и выполнить директиву Mask Subsystem for selection. В случае выполнения команды откроется окно редактирования.

Первая из вкладок окна предназначена для отображения подсистем, вторая — для создания окна диалога входных параметров, третья — для инициализации входных параметров, четвертая — для создания окна справки.

Для блоков Fcn и Fcnl модели (см. Рис.2) создадим две подсистемы. С помощью первой подсистемы введем значения a и d, а второй — значения b и с. Отметим часть схемы, которую мы сделаем подсистемой и из меню, открытого правой кнопкой мыши, выполним Edit->Create Subsystem Selection или из главного меню директиву Diagram->Subsystem и Model Reference.

Ниже приведена схема модели и двух подсистем а также структура подсистем (рис. 3).

Рис. 3. Решение дифференциального уравнения: схема модели с двумя подсистемами

Рис. 3-а. Структурная схема подсистемы для ввод параметров а, d

Рис. 3-б. Структурная схема подсистемы для ввод параметров b, c

Теперь организуем ввод параметров a, d, b, и с. Директивой Diagram->Mask->Create Mask. мы можем запустить окно редактирования модели. Выполним двойной щелчок мышью по блоку подсистемы, откроется окно подсистемы и директивой Diagram->Mask->Create Mask. мы можем запустить окно редактирования модели.

Для формирования окна для ввода параметров в окне Dialog box разместим Groop box и два элемента edit. Директивой Apply рассмотрим вид входных окон (Рис. 4-a и Рис. 4-б).

Mask Editor : Subsystem

Icon & Ports] Parameters & Dialog Initialization Documentation

Controls Dialog box

* Parameter [Type Prompt Name

m Edit 0> Checkbox f(x)=a+duA2 DescGroupVar

3-CJ Parameters Conta inerâ

1=3 Popup (flj Radio button «0» Slider hi #1 ЧИ #2 Input Parameter a Input Parameter d a d

Рис. 4-а. Формирование входного окна: для ввода параметров а и d

Mask Editor : Subsystem!

Icon & Ports I Parameters & Dialog [^Initialization Documentation]

S3 Edit Щ Checkbox Popup Radio button «0» Slider

Type Prompt Name

•CJ p(x) = bu(c+uA2) DescGroupVar

ÉO Parametrs Contain er3

[■mm. Input Parameter b b

H3II #2 Input Parameter с с

Рис. 4-б. Формирование входного окна: для ввода параметров b и c

Двойным щелчком мыши по блоку подсистемы открыть окно, созданное директивой Mask, и ввести значения констант (Рис. 5).

Рис. 5. Вид блоков входных параметров: а и d, b и c

Запустив модель, мы получим фазовую траекторию функции, и графики функций ) У () в зависимости от t (Рис. 6).

Рис. 6. Фазовая траектория функции, и графики функций у() и У ()

в зависимости от

Рассмотрим следующее логистическое дифференциальное уравнение первого порядка у'(0 =-3у(/ -1)(1-у(/)). Ниже приведены модель (Рис.7-а) и результат решения (Рис. 7-б).

Рис. 7-а. Структурная схема решения дифференциального уравнения

Рис. 7-б. Результат решения логистического дифференциального уравнения

Здесь использован блок Transport Delay, который задерживает входной сигнал на фиксированное время. В окне настройки параметров блока указывается время задержки сигнала (Time Delay — 1), начальное значение выходного сигнала (Initial input), объем памяти, где будет записан задержанный сигнал (Buffer size — дано в байтах -1024).

Моделирование линейных дифференциальных уравнений второго порядка. Самый

простой вид свободных колебаний задается посредством уравнения

уравнения состоит из двух блоков интегратора, которые интегрируют входной сигнал два раза.

В системе вынужденные колебания задаются в виде уравнения

блоках с обратной связью t (Рис. 8).

= p(x)y + f (x) . S-модель этого уравнения основана на двух интегральных

Рис. 8. Структурная схема дифференциального уравнения вынужденных колебаний Если уравнение вынужденных колебаний, заданно в виде ^ У = р(х) + у(х) имеет

следующую S- модель (Рис. 9):

Рис. 9. Структурная схема дифференциального уравнения вынужденных колебаний для второго

Особенностью этой модели является обратная связь двух интеграторов, где сигнал от второго интегратора передается на вход первого интеграта. В этой модели уже участвует производная первого порядка данной функции.

вынужденных колебаний имеет вид

В общем случае уравнение

Рассмотрим моделирование задачи свободных и вынужденных колебаний математического маятника.

Если на колебательную систему действуют момент внешней силы и силы трения вязкости, то дифференциальное уравнение, описывающее колебания маятника, может быть записано в следующем виде:

+ 2(—+ с0 sin V = с^в0 sinсt,

где Надоели баннеры? Вы всегда можете отключить рекламу.