Метод возведения обеих частей уравнения в одну и ту же степень
Продолжаем изучать методы решения уравнений. Сейчас мы в деталях разберем метод возведения обеих частей уравнения в одну и ту же степень. Начнем с теории: рассмотрим, для решения каких уравнений применяется метод, опишем, в чем он состоит, приведем теоретическое обоснование метода возведения обеих частей уравнения в одну и ту же степень, запишем соответствующие алгоритмы решения уравнений. После этого сосредоточимся на практике и рассмотрим разнообразные примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень.
Для решения каких уравнений применяется
Метод возведения обеих частей уравнения в одну и ту же степень в первую очередь применяется для решения иррациональных уравнений. Это объясняется тем, что возведение в натуральную и большую единицы степень позволяет избавляться от корней. Например, возведение в степень позволяет избавляться от корней при решении следующих уравнений:
, C≥0 , в частности,
,
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
и дальше — к элементарному уравнению 4−5·x=0 .
, например,
,
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и
, таких как
,
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
- уравнений с двумя, тремя корнями в записи, например,
и
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
- уравнений, в которых под знаком корня находятся другие корни, к примеру,
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
- и это не весь список.
Метод возведения обеих частей уравнения в одну и ту же степень используется и для решения некоторых уравнений, в которых переменная находится в основаниях степеней с дробными показателями. Например, уравнение 
Также метод возведения частей уравнения в степень применяется при решении некоторых степенных уравнений, в которых фигурируют иррациональные показатели. В пример приведем два уравнения 



В чем состоит метод возведения обеих частей уравнения в одну и ту же степень
Метод состоит в переходе к уравнению, которое получается из исходного путем возведения его обеих частей в одну и ту же степень, и нахождении решения исходного уравнения по решению полученного уравнения.
На практике наиболее часто прибегают к возведению обеих частей уравнения в одну и ту же натуральную степень, большую единицы, то есть, в квадрат, куб и т.д. Делается это на базе следующего утверждения:
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень, большую единицы, дает равносильное уравнение (см. равносильные уравнения и уравнения-следствия).
Реже приходится обращаться к возведению обеих частей уравнения в другие степени, в частности, в дробные рациональные и иррациональные. В этих случаях отталкиваются от такого утверждения:
Уравнение A(x)=B(x) , на области допустимых значений переменной x для которого A(x)>0 или A(x)≥0 , B(x)>0 или B(x)≥0 , равносильно уравнению A r (x)=B r (x) , где r – положительное действительное число.
Обоснование метода
Обоснованием метода возведения обеих частей уравнения в одну и ту же степень является доказательство утверждений из предыдущего пункта. Приведем эти доказательства.
Возведение обеих частей уравнения в одну и ту же четную натуральную степень дает уравнение-следствие, а возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Докажем его для уравнений с одной переменной. Для уравнений с несколькими переменными принципы доказательства те же.
Пусть A(x)=B(x) – исходное уравнение и x0 – его корень. Так как x0 является корнем этого уравнения, то A(x0)=B(x0) – верное числовое равенство. Мы знаем такое свойство числовых равенств: почленное умножение верных числовых равенств дает верное числовое равенство. Умножим почленно 2·k , где k – натуральное число, верных числовых равенств A(x0)=B(x0) , это нам даст верное числовое равенство A 2·k (x0)=B 2·k (x0) . А полученное равенство означает, что x0 является корнем уравнения A 2·k (x)=B 2·k (x) , которое получено из исходного уравнения путем возведения его обеих частей в одну и ту же четную натуральную степень 2·k .
Для обоснования возможности существования корня уравнения A 2·k (x)=B 2·k (x) , который не является корнем исходного уравнения A(x)=B(x) , достаточно привести пример. Рассмотрим иррациональное уравнение 





Так доказано, что возведение обеих частей уравнения в одну и ту же четную натуральную степень приводит к уравнению-следствию.
Остается доказать, что возведение обеих частей уравнения в одну и ту же нечетную натуральную степень дает равносильное уравнение.
Покажем, что каждый корень уравнения является корнем уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, и обратно, что каждый корень уравнения, полученного из исходного путем возведения его обеих частей в нечетную степень, является корнем исходного уравнения.
Пусть перед нами уравнение A(x)=B(x) . Пусть x0 – его корень. Тогда является верным числовое равенство A(x0)=B(x0) . Изучая свойства верных числовых равенств, мы узнали, что верные числовые равенства можно почленно умножать. Почленно умножив 2·k+1 , где k – натуральное число, верных числовых равенств A(x0)=B(x0) получим верное числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) , которое означает, что x0 является корнем уравнения A 2·k+1 (x)=B 2·k+1 (x) . Теперь обратно. Пусть x0 – корень уравнения A 2·k+1 (x)=B 2·k+1 (x) . Значит числовое равенство A 2·k+1 (x0)=B 2·k+1 (x0) — верное. В силу существования корня нечетной степени из любого действительного числа и его единственности будет верным и равенство 

Так доказано, что возведение обеих частей иррационального уравнения в нечетную степень дает равносильное уравнение.
Доказанное утверждение пополняет известный нам арсенал, использующийся для решения уравнений, еще одним преобразованием уравнений – возведением обеих частей уравнения в одну и ту же натуральную степень. Возведение в одну и ту же четную степень обеих частей уравнения является преобразованием, приводящим к уравнению-следствию, а возведение в нечетную степень – равносильным преобразованием. На этом преобразовании базируется метод возведения обеих частей уравнения в одну и ту же степень.
Утверждение, касающееся возведения обеих частей уравнения в одну и ту же положительную действительную степень, доказывается аналогично с опорой на единственность степени положительного числа с действительным показателем.
Алгоритмы решения уравнений методом возведения частей в одну и ту же степень
Есть смысл записать три алгоритма решения уравнений методом возведения обеих частей уравнения в одну и ту же степень: первый – для возведения в нечетную степень, второй – для возведения в четную степень, третий – для возведения в ненатуральную положительную степень.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же нечетную степень:
- Обе части уравнения возводятся в одну и ту же нечетную степень 2·k+1 .
- Решается полученное уравнение. Его решение есть решение исходного уравнения.
Алгоритм решения уравнений методом возведения обеих частей в одну и ту же четную степень:
- Обе части уравнения возводятся в одну и ту же четную степень 2·k .
- Решается полученное уравнение.
- Если полученное уравнение не имеет корней, то делается вывод об отсутствии корней у исходного уравнения.
- Если полученное уравнение имеет корни, то проводится отсеивание посторонних корней любым методом, не завязанным на области допустимых значений, например, через проверку подстановкой.
Обратите внимание: этот алгоритм, в отличие от предыдущего, содержит пункт, касающийся отсеивания посторонних корней. Это связано с тем, что возведение обеих частей уравнения в одну и ту же нечетную степень приводит к равносильному уравнению, а возведение обеих частей уравнения в четную степень в общем случае приводит к уравнению-следствию. Поэтому, в результате возведения в нечетную степень посторонние корни не возникают, а при возведении в четную степень посторонние корни могут появиться. Таким образом, при возведении частей уравнения в четную степень возникает необходимость в отсеивании посторонних корней. Почему отсеивание посторонних корней в этом случае нужно проводить методом, не использующим ОДЗ? Потому что возведение обеих частей уравнения в четную степень может приводить к появлению посторонних корней в пределах ОДЗ, и отсеять их по ОДЗ или по условиям ОДЗ невозможно.
Наконец, запишем алгоритм решения уравнений методом возведения обеих частей в одну и ту же положительную дробную рациональную или иррациональную степень:
- Убеждаемся, что выражения в левой и правой части уравнения не принимают отрицательных значений на ОДЗ для решаемого уравнения.
- Возводим обе части уравнения в одну и ту же положительную степень.
- Решаем полученное уравнение. Его решение дает искомое решение исходного уравнения.
Примеры решения уравнений методом возведения обеих частей уравнения в одну и ту же степень
Большое количество попадающих под разбираемую тему примеров с подробными решениями приведено в статье решение иррациональных уравнений методом возведения обеих частей в одну и ту же степень. В добавление к этим примерам стоит разобрать решение уравнения через возведение обеих частей уравнения в одну и ту же степень, не являющуюся натуральным числом.
Решите уравнение
Решать заданное уравнение можно несколькими разными методами. Например, можно провести решение методом логарифмирования. Также можно преобразовать уравнение к виду 

Учитывая свойство степени в степени (см. свойства степеней), несложно догадаться, что избавиться от иррациональных показателей позволяет возведение обеих частей уравнения в степень 

Итак, проводим возведение обеих частей уравнения 


Решаем полученное уравнение:
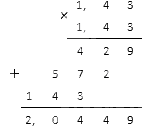
Так мы пришли к кубическому уравнению x 3 −x 2 +2=0 . Один его корень x=−1 легко подбирается. Разделив многочлен x 3 −x 2 +2 на двучлен x+1 , получаем возможность представить кубическое уравнение в виде (x+1)·(x 2 −2·x+2)=0 . Квадратное уравнение x 2 −2·x+2=0 не имеет решений, так как его дискриминант отрицательный. Из этого заключаем, что уравнение x 3 −x 2 +2=0 имеет единственный корень x=−1 .
В процессе решения мы дважды отмечали, что нам будет необходимо сделать проверку найденных корней. Сейчас пришло это время. Проверку выполним через подстановку найденного корня x=−1 в исходное уравнение 
Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
Возведение в степень: правила, примеры
Мы разобрались, что вообще из себя представляет степень числа. Теперь нам надо понять, как правильно выполнять ее вычисление, т.е. возводить числа в степень. В этом материале мы разберем основные правила вычисления степени в случае целого, натурального, дробного, рационального и иррационального показателя. Все определения будут проиллюстрированы примерами.
Понятие возведения в степень
Начнем с формулирования базовых определений.
Возведение в степень — это вычисление значения степени некоторого числа.
То есть слова «вычисление значение степени» и «возведение в степень» означают одно и то же. Так, если в задаче стоит «Возведите число 0 , 5 в пятую степень», это следует понимать как «вычислите значение степени ( 0 , 5 ) 5 .
Теперь приведем основные правила, которым нужно придерживаться при таких вычислениях.
Как возвести число в натуральную степень
Вспомним, что такое степень числа с натуральным показателем. Для степени с основанием a и показателем n это будет произведение n -ного числа множителей, каждый из которых равен a . Это можно записать так:
Чтобы вычислить значение степени, нужно выполнить действие умножения, то есть перемножить основания степени указанное число раз. На умении быстро умножать и основано само понятие степени с натуральным показателем. Приведем примеры.
Условие: возведите — 2 в степень 4 .
Решение
Используя определение выше, запишем: ( − 2 ) 4 = ( − 2 ) · ( − 2 ) · ( − 2 ) · ( − 2 ) . Далее нам нужно просто выполнить указанные действия и получить 16 .
Возьмем пример посложнее.
Вычислите значение 3 2 7 2
Решение
Данную запись можно переписать в виде 3 2 7 · 3 2 7 . Ранее мы рассматривали, как правильно умножать смешанные числа, упомянутые в условии.
Выполним эти действия и получим ответ: 3 2 7 · 3 2 7 = 23 7 · 23 7 = 529 49 = 10 39 49
Если в задаче указана необходимость возводить иррациональные числа в натуральную степень, нам потребуется предварительно округлить их основания до разряда, который позволит нам получить ответ нужной точности. Разберем пример.
Выполните возведение в квадрат числа π .
Решение
Для начала округлим его до сотых. Тогда π 2 ≈ ( 3 , 14 ) 2 = 9 , 8596 . Если же π ≈ 3 . 14159 , то мы получим более точный результат: π 2 ≈ ( 3 , 14159 ) 2 = 9 , 8695877281 .
Отметим, что необходимость высчитывать степени иррациональных чисел на практике возникает сравнительно редко. Мы можем тогда записать ответ в виде самой степени ( ln 6 ) 3 или преобразовать, если это возможно: 5 7 = 125 5 .
Отдельно следует указать, что такое первая степень числа. Тут можно просто запомнить, что любое число, возведенное в первую степень, останется самим собой:
Это понятно из записи 
От основания степени это не зависит.
Так, ( − 9 ) 1 = − 9 , а 7 3 , возведенное в первую степень, останется равно 7 3 .
Как возвести число в целую степень
Для удобства разберем отдельно три случая: если показатель степени — целое положительное число, если это ноль и если это целое отрицательное число.
В первое случае это то же самое, что и возведение в натуральную степень: ведь целые положительные числа принадлежат ко множеству натуральных. О том, как работать с такими степенями, мы уже рассказали выше.
Теперь посмотрим, как правильно возводить в нулевую степень. При основании, которое отличается от нуля, это вычисление всегда дает на выходе 1 . Ранее мы уже поясняли, что 0 -я степень a может быть определена для любого действительного числа, не равного 0 , и a 0 = 1 .
5 0 = 1 , ( — 2 , 56 ) 0 = 1 2 3 0 = 1
0 0 — не определен.
У нас остался только случай степени с целым отрицательным показателем. Мы уже разбирали, что такие степени можно записать в виде дроби 1 a z , где а — любое число, а z — целый отрицательный показатель. Мы видим, что знаменатель этой дроби есть не что иное, как обыкновенная степень с целым положительным показателем, а ее вычислять мы уже научились. Приведем примеры задач.
Возведите 2 в степень — 3 .
Решение
Используя определение выше, запишем: 2 — 3 = 1 2 3
Подсчитаем знаменатель этой дроби и получим 8 : 2 3 = 2 · 2 · 2 = 8 .
Тогда ответ таков: 2 — 3 = 1 2 3 = 1 8
Возведите 1 , 43 в степень — 2 .
Решение
Переформулируем: 1 , 43 — 2 = 1 ( 1 , 43 ) 2
Вычисляем квадрат в знаменателе: 1,43·1,43. Десятичные дроби можно умножить таким способом:
В итоге у нас вышло ( 1 , 43 ) — 2 = 1 ( 1 , 43 ) 2 = 1 2 , 0449 . Этот результат нам осталось записать в виде обыкновенной дроби, для чего необходимо умножить ее на 10 тысяч (см. материал о преобразовании дробей).
Ответ: ( 1 , 43 ) — 2 = 10000 20449
Отдельный случай — возведение числа в минус первую степень. Значение такой степени равно числу, обратному исходному значению основания: a — 1 = 1 a 1 = 1 a .
Пример: 3 − 1 = 1 / 3
9 13 — 1 = 13 9 6 4 — 1 = 1 6 4 .
Как возвести число в дробную степень
Для выполнения такой операции нам потребуется вспомнить базовое определение степени с дробным показателем: a m n = a m n при любом положительном a , целом m и натуральном n .
Таким образом, вычисление дробной степени нужно выполнять в два действия: возведение в целую степень и нахождение корня n -ной степени.
У нас есть равенство a m n = a m n , которое, учитывая свойства корней, обычно применяется для решения задач в виде a m n = a n m . Это значит, что если мы возводим число a в дробную степень m / n , то сначала мы извлекаем корень n -ной степени из а , потом возводим результат в степень с целым показателем m .
Проиллюстрируем на примере.
Вычислите 8 — 2 3 .
Решение
Способ 1. Согласно основному определению, мы можем представить это в виде: 8 — 2 3 = 8 — 2 3
Теперь подсчитаем степень под корнем и извлечем корень третьей степени из результата: 8 — 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4
Способ 2. Преобразуем основное равенство: 8 — 2 3 = 8 — 2 3 = 8 3 — 2
После этого извлечем корень 8 3 — 2 = 2 3 3 — 2 = 2 — 2 и результат возведем в квадрат: 2 — 2 = 1 2 2 = 1 4
Видим, что решения идентичны. Можно пользоваться любым понравившимся способом.
Бывают случаи, когда степень имеет показатель, выраженный смешанным числом или десятичной дробью. Для простоты вычислений его лучше заменить обычной дробью и считать, как указано выше.
Возведите 44 , 89 в степень 2 , 5 .
Решение
Преобразуем значение показателя в обыкновенную дробь: 44 , 89 2 , 5 = 44 , 89 5 2 .
А теперь выполняем по порядку все действия, указанные выше: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 = = 1350125107 100000 = 13 501 , 25107
Ответ: 13 501 , 25107 .
Если в числителе и знаменателе дробного показателя степени стоят большие числа, то вычисление таких степеней с рациональными показателями — довольно сложная работа. Для нее обычно требуется вычислительная техника.
Отдельно остановимся на степени с нулевым основанием и дробным показателем. Выражению вида 0 m n можно придать такой смысл: если m n > 0 , то 0 m n = 0 m n = 0 ; если m n 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную — значения не имеет: 0 — 4 3 .
Как возвести число в иррациональную степень
Необходимость вычислить значение степени, в показателе которой стоит иррациональное число, возникает не так часто. На практике обычно задача ограничивается вычислением приблизительного значения (до некоторого количества знаков после запятой). Обычно это считают на компьютере из-за сложности таких подсчетов, поэтому подробно останавливаться на этом не будем, укажем лишь основные положения.
Если нам нужно вычислить значение степени a с иррациональным показателем a , то мы берем десятичное приближение показателя и считаем по нему. Результат и будет приближенным ответом. Чем точнее взятое десятичное приближение, тем точнее ответ. Покажем на примере:
Вычислите приближенное значение 2 в степени 1,174367.
Решение
Ограничимся десятичным приближением a n = 1 , 17 . Проведем вычисления с использованием этого числа: 2 1 , 17 ≈ 2 , 250116 . Если же взять, к примеру, приближение a n = 1 , 1743 , то ответ будет чуть точнее: 2 1 , 174367 . . . ≈ 2 1 , 1743 ≈ 2 , 256833 .
http://skysmart.ru/articles/mathematic/pokazatelnye-uravneniya
http://zaochnik.com/spravochnik/matematika/stepeni/vozvedenie-v-stepen/
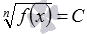 , C≥0 , в частности,
, C≥0 , в частности,  ,
,  и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению
и т.п. Возведение в квадрат обеих частей первого уравнения позволяет перейти к уравнению 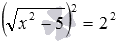 , и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению
, и дальше – к сравнительно простому уравнению без знаков корней x 2 −5=4 . Аналогично, возведение обеих частей второго уравнения в шестую степень приводит к уравнению 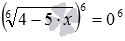 и дальше — к элементарному уравнению 4−5·x=0 .
и дальше — к элементарному уравнению 4−5·x=0 .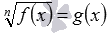 , например,
, например,  ,
,  и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.
и др. В первом случае избавиться от корня позволяет возведение обеих частей уравнения в квадрат, а во втором случае – в куб.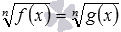 и
и  , таких как
, таких как 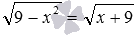 ,
, 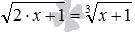 и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень.
и подобные им. Для первого уравнения напрашивается возведение его обеих частей в квадрат, для второго – в шестую степень. и
и  . В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала.
. В таких случаях для избавления от знаков радикалов к возведению обеих частей уравнения в одну и ту же степень приходится обращаться дважды: первый раз в самом начале, второй раз – после преобразований и уединения радикала. . Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.
. Здесь также к возведению обеих частей уравнения в одну и ту же степень приходится прибегать два раза.