Как выбрать модель для регрессионного уравнения

Каталог статей

Многие наши клиенты, которые обращаются к нам за обработкой статистических данных для диссертаций, в частности, за услугами по построению регрессионных моделей, спрашивают, какой вид, какую форму будет иметь прогнозное, регрессионное уравнение. Такие вопросы звучат по-разному. Например, клиенты ссылаются на некоторые публикации, где была выбрана распространенная модель линейной регрессии и, очевидно, ждут такого же результата. Другие заказчики, напротив, просят построить сложную, нестандартную модель, учитывающую все независимые параметры и дающую минимальную ошибку. Все эти требования вполне понятны и объяснимы.

Линейная регрессия

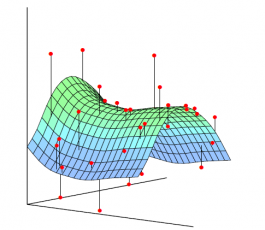
Давайте посмотрим, как же все-таки на самом деле осуществляется выбор модели. В первую очередь поговорим о линейной модели. У неё есть минусы и плюсы. С одной стороны, это самый простой вид регрессии, который легко строится и также легко интерпретируется. Коэффициенты модели показывают, насколько и в каком направлении связаны независимая и зависимые переменные. Однако очевидный минус такой модели — большие отклонения от исходных данных, которые, как правило, распределены по какой-либо более изощренной кривой и никак не хотят укладываться на одну прямую линию.

Иные виды регрессионных моделей

Существует большое число моделей регрессии разного вида. Начиная, от также вполне распространенных экспоненциальных, полиномиальных, степенных, гиперболических, заканчивая изощренными аддитивными моделями, которые могут представлять собой разные сложные функции на разных участках области данных.

Ограничения регрессионного анализа

Нужно понимать, что построение регрессионного уравнения — задача изначально, имеющая свои ограничения. Основное ограничение — первоначальный набор данных. Мы знаем о данных только то, что прогнозируемая величина принимает определенные значения в заданных точках, а пытаемся предсказать, каковы ее значения на всей области.

Вид модели и метод наименьших квадратов

Например, если мы оцениваем качество модели распространенным методом наименьших квадратов по формуле RSS = sum (y_i — f(x_i)) 2 , то для уменьшения RSS подойдут любые функции f(x), которые принимают значения y_i в точках x_i. При этом во всех остальных точках они в принципе могут принимать какие угодно значения.

Далее, исследователь уже самостоятельно выбирает, какую форму уравнения лучше задать именно в данном контексте. И в принципе выбор регрессионного уравнения — это фактически выбор накладываемых на функцию ограничений. При этом решений у этой задачи может быть множество.

Понравилась публикация? Поделитесь ей в соцсетях:

10. Выбор вида регрессионной модели и оценка ее параметров

На данном этапе устанавливается однофакторная или многофакторная будет строиться модель и вид модели (линейный или нелинейный).

Обоснование вида модели состоит в выборе вида функции (некоторого аналитического выражения), с помощью которого можно будет описать изменение исследуемого показателя под воздействием факторов.

К обоснованию вида функции идут двумя путями: Теоретическим (анализируя экономическую природу 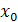и , выдвигается гипотеза о характере изменения показателя под действием фактора) И эмпирическим (закон изменения результативного показателя под действием фактора устанавливается путем анализа совокупности фактических данных по полям корреляции).

Наиболее употребительными выражениями при описании связи одного фактора и исследуемого показателя являются:

— Уравнение прямой — — Уравнение параболы — — Уравнение гиперболы —

После обоснования парных взаимосвязей переходят к записи многофакторных моделей. В экономических исследованиях чаще всего применяется линейная многофакторная модель —

В качестве нелинейных моделей применяются

— Мультипликативная модель — или

Для оценки значений параметров регрессионной модели чаще всего используется Метод наименьших квадратов (МНК).Этот метод можно применить как для линейных моделей, так и для нелинейных, допускающих преобразование их к линейному виду путем замены переменных или дифференцированием.

При использовании МНК делаются определенные предпосылки относительно случайной составляющей ε. В модели случайная составляющая ε представляет собой ненаблюдаемую величину. Поэтому в задачу регрессионного анализа входит не только построение самой модели, но и исследование случайных отклонений , т. е. остаточных величин.

Остатки представляют собой независимые случайные величины, и их среднее значение равно 0; они имеют одинаковую (постоянную) дисперсию и подчиняются нормальному распределению.

Статистические проверки параметров регрессии, показателей корреляции основаны на непроверяемых предпосылках распределения случайной составляющей . Связано это с тем, что оценки параметров регрессии должны отвечать определенным критериям: быть Несмещенными, состоятельными и эффективными. Эти свойства оценок, полученных по МНК, имеют чрезвычайно важное практическое значение в использовании результатов регрессии и корреляции.

Коэффициенты регрессии, найденные из системы нормальных уравнений, представляют собой выборочные оценки характеристики силы связи. Их несмещенность является желательным свойством, т. к. только в этом случае они могут иметь практическую значимость.

Несмещенность оценки означает, что математическое ожидание остатков равно нулю. Оценки считаются Эффективными, если они характеризуются наименьшей дисперсией. Поэтому несмещенность оценки должна дополняться минимальной дисперсией. Состоятельность оценок характеризует увеличение их точности с увеличением объема выработки.

Указанные критерии оценок (несмещенность, состоятельность, эффективность) обязательно учитываются при разных способах оценивания. Метод наименьших квадратов строит оценки регрессии на основе минимизации суммы квадратов остатков ().

Исследование остатков предполагают проверку наличия следующих пяти предпосылок МНК:

— случайный характер остатков; — нулевая средняя величина остатков, не зависящая от ; — гомоскедастичность – дисперсия каждого отклонение одинакова для всех значений х; — отсутствие автокорреляции остатков, т. е. значения остатков — остатки подчиняются нормальному распределению.

С цель проверки случайного характера остатков строится график зависимости остатков от теоретических значений результативного признака .

Если на графике нет направленности в расположении точек , то остатки представляют собой случайные величины и МНК оправдан. Также возможны следующие случаи: если зависит от теоретического значения, то:

Вторая предпосылка МНК относительно нулевой средней величины остатков означает, что . Это выполнимо для линейных моделей и моделей, нелинейных относительно включаемых переменных. Для обеспечения несмещенности оценок коэффициентов регрессии, полученных МНК, необходимо выполнение условий независимости случайных остатков и переменных х, что исследуется в рамках соблюдения второй предпосылки МНК. С целью проверки выполнение этой предпосылки строится график зависимости случайных остатков ε от факторов, включенных в регрессию . Если расположение остатков на графике не имеет направленности, то они независимы от значений . Если же график показывает наличие зависимости и , то модель неадекватна.

Предпосылка о нормальном распределении остатков позволяет проводить проверку параметров регрессии и корреляции с помощью критериев t и F. Вместе с тем оценки регрессии, найденные с применением МНК, обладают хорошими свойствами даже при отсутствии нормального распределения остатков, т. е. при нарушении пятой предпосылки метода наименьших квадратов.

В соответствии с третьей предпосылкой МНК требуется, чтобы дисперсия остатков была гомоскедастичной. Это означает, что для каждого значения фактора остатки имеют одинаковую дисперсию. Если это условие применения МНК не соблюдается, то имеет место гетероскедастичность. Используя трехмерной изображение, рассмотрим отличие гомо — и гетероскедастичности.

Наличие гетероскедастичности будет сказываться на уменьшении эффективности оценок , в частности, становится затруднительным использование формулы стандартной ошибки коэффициента регрессии, предполагающей единую дисперсию остатков для любых значений фактора.

Наличие гетероскедастичности в остатках регрессии можно проверить с помощью ранговой корреляции Спирмэна. Суть проверки заключается в том, что в случае гетероскедастичности абсолютные остатки коррелированы со значениями фактора . Эту корреляцию можно измерять с помощью коэффициента ранговой корреляции Спирмэна:

, (1.35)

Где ρ – абсолютная разность между рангами значений и .

Статистическую значимость ρ можно определить с помощью t-критерия:

. (1.36)

Принято считать, что если , то корреляция между и статистически значима, т. е. имеет место гетероскедастичность остатков. В противном случае принимается гипотеза об отсутствии гетероскедастичности остатков.

При построении регрессионных моделей чрезвычайно важно соблюдение четвертой предпосылки МНК – отсутствие автокорреляции остатков, т. е. распределения остатков и независимы. Автокорреляция остатков означает наличие корреляции между остатками текущих и предыдущих (последующих) наблюдений. Находится коэффициент корреляции между и , и если он окажется существенно отличным от нуля, то остатки автокоррелированы и функция плотности вероятности F(ε) зависит от j-ой точки наблюдения и от распределения значений остатков в других точках наблюдения.

Отсутствие автокорреляции остатков обеспечивает состоятельность и эффективность оценок коэффициентов регрессии.

До сих пор в качестве факторов рассматривались экономические переменные, принимающие количественные значения в некотором интервале. Вместе с тем может оказаться необходимым включить в модель фактор, имеющий два или более качественных уровней. Это могут быть разного рода атрибутивные признаки, такие, например, как профессия, пол, образование, климатические условия, принадлежность к определенному региону. Для того, чтобы ввести такие переменные в регрессионную модель, им должны быть присвоены те или иные цифровые метки, т. е. качественные переменные необходимо преобразовать в количественные. Такого вида сконструированные переменные в эконометрике принято называть фиктивными переменными.

Качественные признаки могут приводить к неоднородности исследуемой совокупности, что может быть учтено при моделировании двумя путями:

— регрессия строится для каждой качественно отличной группы единиц совокупности, т. е. для каждой группы в отдельности, чтобы преодолеть неоднородность единиц общей совокупности; — общая регрессионная модель строится для совокупности в целом, учитывающей неоднородность данных. В этом случае в регрессионную модель вводятся фиктивные переменные, т. е. строится регрессионная модель с переменной структурой, отражающей неоднородность данных.

Качественный фактор может иметь только два состояния, которым будут соответствовать 1 и 0. Если же число градаций качественного признака-фактора превышает два, то в модель вводится несколько фиктивных переменных, число которых должно быть меньше числа качественных градаций. Только при соблюдении этого положения матрица исходных фиктивных переменных не будет линейно зависима и возможна оценка параметров модели.

Коэффициент регрессии при фиктивной переменной интерпретируется как среднее изменение зависимой переменной при переходе от одной категории к другой при неизменных значениях остальных параметров. На основе t-критерия Стьюдента делается вывод о значимости влияния фиктивной переменной, существенности расхождения между категориями.

Please wait.

We are checking your browser. medium.com

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6e27654a18da3a55 • Your IP : 85.95.188.35 • Performance & security by Cloudflare