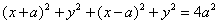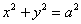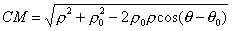Как вывести уравнение геометрического места точек

Как вывести уравнение геометрического места точек

Глава 10. Вывод уравнений заранее данных линий

В задачах предыдущего параграфа линия определялась при помощи данного уравнения. Здесь мы будем иметь задачи противоположного характера; в каждой из них линия определяется чисто геометрически, а уравнение ее требуется найти.

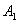
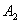
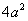
ПРИМЕР 1. В декартовой прямоугольной системе координат вывести уравнение геометрического места точек, сумма квадратов расстояний которых до двух данных точек (-а; 0) и (а; 0) есть величина постоянная, равная .

РЕШЕНИЕ. Обозначим буквой М произвольную точку линии, буквами х и у обозначим координаты этой точки. Так как точка М может занимать на линии любое положение то х и у являются переменными величинами; их называют текущими координатами.

Запишем геометрическое свойство линии символически:

(1).

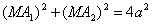
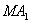
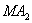
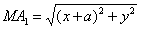
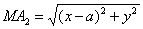
В этом отношении при движении точки М могут меняться длины и . Выразим их через текущие координаты точки М:

, (2)

Подставив полученные выражения в равенство (1), найдем уравнение, связывающее координаты х, у точки М:

Это и есть уравнение данной линии.

Действительно, для каждой точки М, лежающей на этой инии, выполняется условие (1) и, следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на линии, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Однако уравнение (2) можно упростить; раскрывая скобки и приводя подобные члены, получим уравнение данной линии в виде:

Теперь легко понять, что данная линия есть окружность с центром в начале координат и радиусом, равным а.

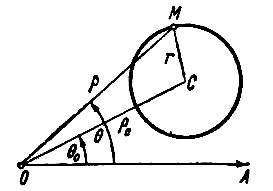
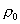
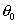
ПРИМЕР 2. В полярной системе координат вывести уравнение окружности, которая имеет центр С( ; ) и радиус r (см. рис.).

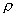
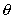
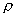
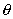
РЕШЕНИЕ. Олозначим буквой М произвольную точку окружности, буквами и — ее полярные координаты. Так как точка М может занимать на окружности любое положение, то и являются переменными величинами. Как и в случае декартовой системы, их называют текущими координатами.

Все точки окружности отстоят от центра на расстоянии r ; запишем это условие символически:

(1).

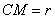
Выразим СМ через текущие координаты точки М (воспользуемся теоремой косинусов):

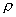
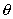
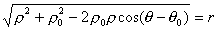
Подставив полученное выражение в равенство (1), найдем уравнение, связывающее координаты , точки М:

(2)

Это и есть уравнение данной окружности.

Действительно, для каждой точки М, лежащей на данной окружности, выполняется условие (1) и , следовательно, координаты точки М будут удовлетворять уравнению (2); для каждой точки М, не лежащей на данной окружности, не будет выполняться условие (1) и, следовательно, ее координаты не будут удовлетворять уравнению (2).

Таким образом, задача решена. Можно лишь несколько упростить полученное уравнение и представить его в виде, свободным от радикала:

.

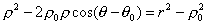
Как вывести уравнение геометрического места точек

Найти уравнение геометрического места точек, произведение расстояний которых до двух данных точек A и B есть величина постоянная, равная a 2 . Длину AB считать равной 2a.

Проведем вывод уравнения в прямоугольных координатах. Направим ось Ox по прямой, соединяющей A и B, как обычно, вправо, начало координат поместим в середине отрезка AB, ось Oy направим вверх по перпендикуляру к оси Ox. Длина отрезка AB по условию равна 2a (AB = 2a); тогда точки A и B будут иметь координаты: A(-a, 0); B(a, 0). Пусть точка M принадлежит кривой. Ее координаты обозначим через x и y (см. рисунок).

Из условия задачи AM * BM = a 2 . По формуле расстояния между двумя точками

Возведем обе части этого уравнения в квадрат:

Конспект урока по геометрии в 9-м физико-математическом классе по теме: «Эллипс как геометрическое место точек»

Разделы: Математика

Цель: сформировать понятие об эллипсе как о геометрическом месте точек; вывести каноническое уравнение эллипса, показать применение полученных знаний об эллипсе к решению задач; показать применение геометрических знаний к реальным процессам в природе; углубить знание по теме “Метод координат”.

Ход урока

Организационный момент. Мотивация изучения нового материала.

Начать урок можно с цитаты венгерского математика Дьердье Пойа: “Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия”.

Действительно, в решении любой задачи присутствует крупица открытия и прежде, чем совершить большое научное открытие, нужно постоянно работать над небольшими задачами, каждая из которых приближает к решению больших задач, так как большое начинается с малого.

И сегодня на уроке мы попробуем совершить небольшое открытие, которое будет состоять в решении следующей задачи: найти ГМТ, сумма расстояний от которых до двух заданных точек F₁, F₂ есть величина постоянная, большая, чем F₁F₂.

Цель нашего урока: выяснить, что за линия удовлетворяет этому множеству и каким уравнением она задается, а также посмотреть применение полученных знаний к решению задач.

Актуализация знаний учащихся.

Прежде чем приступить к решению задачи (небольшому открытию), необходимо вспомнить материал, связанный с ГМТ.

• Что такое ГМТ? (ГМТ – фигура, которая состоит из всех точек плоскости, обладающим определенным свойством).
• Какие фигуры, определяются через ГМТ? (Например, окружность – ГМТ равноудаленных от данной; гипербола – ГМТ для каждой из которых абсолютная величина разности до двух данных точек F₁ и F₂ имеет одно и тоже значение, меньшее, чем F₁F₂.).
• При выводе уравнений этих линий была использована формула расстояния между двумя точками
• Представьте, что вам нужно начертить окружность на песке (циркуля нет). Как, пользуясь только подручными материалами это сделать (описать процесс построения окружности с помощью веревки).

Проведение практической работы.

Затем возвращаемся к задаче, которую решаем и пробуем практически выяснить, что это за линия. Сделать рисунок и с помощью него составить план построения линии, проанализировав условие задачи.

Т. о., нужно построить линию, для которой сумма МF₁+MF₂ постоянная: значения слагаемых меняются (но всегда неотрицательны, т. к. это расстояния между двумя точками), а значение суммы постоянно. Длины отрезков в данном случае удобно измерять с помощью нити. Совместно с учащимися составляется план (по аналогии с построением окружности с помощью веревочки).

• Прикрепим концы нити с помощью кнопок к точкам F₁ и F₂.
• Карандашом натянем нить так, чтобы его острие касалось бумаги.
• Будем перемещать карандаш по бумаге так, чтобы нить оставалась натянутой.
• Вычерчиваем карандашом линию.

Учащиеся выполняют практическую работу по заранее заготовленным моделям и получают на бумаге линию.

Получившаяся линия называется эллипсом, учащиеся с ней встречались в курсе черчения. Итак, в тетради записываем число и тему урока: “Эллипс как геометрическое место точек”. В начале урока мы с вами сформулировали цель и задачи: что за линия удовлетворяет данному множеству, мы выяснили, осталось вывести ее уравнение и посмотреть, как применяются полученные знания к решению задач.

Изучение нового материала.

Исходя из поставленной задачи, сформулировать определение эллипса.

Эллипс – ГМТ, сумма расстояний, от которых до двух заданных точек F₁, F_2, есть величина постоянная, большая, чем F₁F₂. Точки F₁ и F₂ называются фокусами эллипса.

Выведем уравнение эллипса с помощью метода координат: ввести удобным образом систему координат и в ней найти координаты всех задействованных точек.

Дано:

1) Введем прямоугольную систему координат так чтобы фокусы F₁ и F₂ лежали на оси абсцисс, а начало координат совпадало с серединой отрезка F₁F₂. Тогда F₁(–c; 0), F₂(c; 0).

2) .

.

3) .

4), т. е. координаты точки М не удовлетворяют уравнению (*).

5) Уравнение (*) – уравнение эллипса в выбранной системе координат. Преобразуем его к более простому виду.

.

Так как, а 2 – с 2 >0, то пусть а 2 – с 2 = b 2

6) Получили уравнение эллипса , где , которое называется каноническим уравнением. Величины а и b называются соответственно большой и малой полуосями эллипса – т.е., расстояния от центра эллипса до наиболее и наименее удаленных точек. Названия “большая” и “малая” объясняются тем, что а>b.

Ответ:

“Эллипс” в переводе с греческого означает “выпадение”, “опущение”. Точки F₁ и F₂ называются фокусами эллипса, что в переводе с латинского означает “огонь”, “очаг”. Происхождения этих названий связаны с оптическими свойствами эллипса, которые вы будете изучать в курсе физики.

Первичное закрепление изученного материала.

а =3; b = 2; с =.

.

Пересекаются в четырех точках , .

Пересекаются в двух точках (0; –2), .

Поставить оценки за работу на уроке.

Подведение итогов урока.

Как вы знаете, все математические объекты тем или иным способом находят свое применение в практике. Эллипс имеет самое непосредственное отношение к Вселенной. Еще Иоганн Кеплер (1571 – 1630) – немецкий астроном обнаружил, что планеты Солнечной системы движутся вокруг Солнца не по окружностям, как думали раньше, а по эллипсам, причем Солнце находится в одном из фокусов этих эллипсов. Посмотрите какое открытие мы с вами сегодня совершили – решили задачу о множестве точек, а это ГМТ имеет отношение к Вселенной, в которой все существует (и это только задача!).

Вы обратили внимание на тему “Эллипс как геометрическое место точек”? Что это значит? Может быть, эллипс можно рассматривать иначе? (провести аналогию с рассмотрением гиперболы в курсе алгебры и геометрии). Действительно эллипс можно рассматривать и с другой точки зрения – с точки зрения конических сечений. И не только эллипс, но гиперболу и параболу. В старших классах мы докажем, что эллипс, гиперболу и параболу можно получить как сечение конуса плоскостью. Поэтому их и называют коническими сечениями. Конические сечения изучали еще древнегреческие геометры, и теория конических сечений была одной из вершин античной геометрии. А уравнения этих линий были выведены гораздо позднее, когда стал применяться метод координат.

Домашнее задание. Составить и решить три задачи по теме урока.

Подвести итоги урока, обсуждая с учащимися следующие вопросы.

• Что нового вы узнали на уроке? Или, какие моменты для вас были наиболее интересными?
• Какая из задач для вас была наиболее легкой, трудной, интересной?
• Поднимите руки те, кто доволен своей работой на уроке.

Вернутся к цитате, с которой начинался урок: “Крупное научное открытие дает решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия”. Еще раз обсудить ее.

Список использованной литературы.