Как задать уравнение параллелограмма в c

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

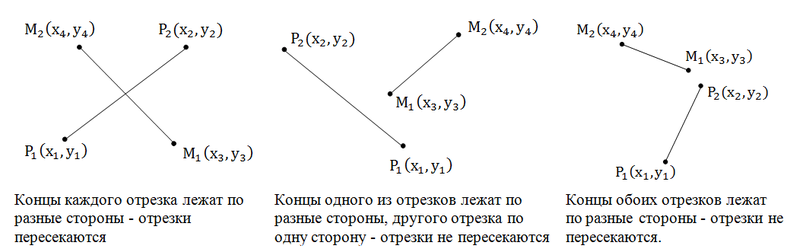
Определить пересекаются ли два отрезка.

Решение
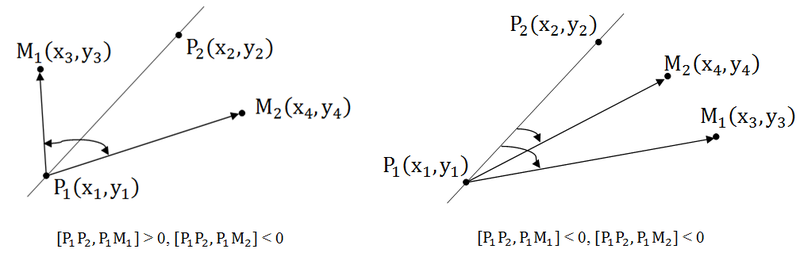
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
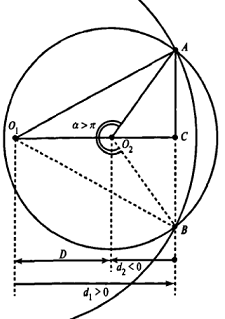
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

Вычислительная геометрия

Напомним, что отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Вектор на плоскости можно задать двумя числами — его координатами по горизонтали и вертикали.

vector

Помимо очевидных сложения, вычитания и умножения на константу (скаляр — одно число), у векторов можно ввести и свои особенные операции, которые нам упростят жизнь.

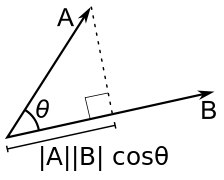
Скалярное произведение (англ. dot product) — произведение длин векторов на косинус угла между ними. Для него справедлива следующая формула:

\[ a \cdot b = x_a x_b + y_a y_b \]

Она доказывается муторно и чисто технически, так что мы это делать не будем.

Геометрически, она равна проекции вектора \(b\) на вектор \(a\) , помноженный на длину \(а\) :

dot

У него есть полезные свойства:

• Скалярное произведение симметрично ( \(a \cdot b = b \cdot a\) ).
• Перпендикулярные вектора должны иметь нулевое скалярное произведение.
• Если угол острый, то скалярное произведение положительное.
• Если угол тупой, то скалярное произведение отрицательное.

Векторное произведение (англ. cross product) — произведение длин векторов на синус угла между ними, причём знак этого синуса зависит от порядка операндов. Оно тоже удобно выражается в координатах:

\[ a \times b = x_a y_b — y_a x_b \]

Геометрически, это ориентированный объем параллелограмма, натянутого на вектора \(a\) и \(b\) :

cross

• Векторное произведение антисимметрично: \(a \times b = — (b \times a)\) .
• Коллинеарные вектора должны иметь нулевое векторное произведение.
• Если \(b\) «слева» от \(a\) , то векторное произведение положительное.
• Если \(b\) «справа» от \(a\) , то векторное произведение отрицательное.

Вообще говоря, векторное произведение определяется не так. Оно определено как вектор такой же длины, но перпендикулярный обоим исходным векторам. Это имеет применение в трёхмерной геометрии и физике, но нам об этом думать не надо.

Всякие проверки

Благодаря этим свойствам, почти все проверки в геометрии можно описать через них, а не уравнениями.

Принадлежность точки треугольнику. Пусть у нас есть треугольник \(ABC\) (заданный против часовой стрелки) и точка \(P\) . Тогда она должна лежать слева от всех трёх векторов \(AB\) , \(BC\) и \(CA\) . Это условие задаст пересечение трёх полуплоскостей, которое и будет нужным треугольником.

\[ \text

\iff \begin (B-A) \times (P-A) \geq 0 \\ (C-B) \times (P-B) \geq 0 \\ (A-C) \times (P-C) \geq 0 \\ \end \]

Площадь треугольника. Можно пользоваться готовыми формулами, а можно и свойством векторного произведения.

Площадь произвольного многоугольника. Если многоугольник задан последовательностью вершин в каком-то порядке, то можно считать так: для каждого ребра добавим его ориентированную площадь от начала координат. Какие-то слагаемые будут положительными (которые на последнем слое, а какие-то — отрицательными).

any

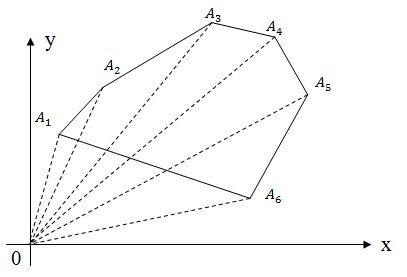
Забудьте о формуле Герона и всегда считайте площади через векторное произведение.

Кстати, из формулы для площади треугольника следует, что площадь любой фигуры будет либо целым числом, либо рациональным с двойкой в знаменателе. Часто в в задачах входные данные целочисленные, и, чтобы оставаться в целых числах, когда мы считаем какую-нибудь площадь, иногда имеет смысл умножить все входные числа на \(2\) (см. «точность»).

Проверка на выпуклость. Можно пройтись по сторонам многоугольника и проверять векторным произведением, что мы поворачиваем всегда в одну сторону, то есть для всех последовательных точек \(a\) , \(b\) , \(c\) проверить, что \((b-a)\times(c-a) > 0\) .

Пересекаются ли отрезки.

segments

Уравнение прямой

Прямую можно задать уравнением вида \(Ax + By + C = 0\) . Полуплоскость можно задать таким же неравенством.

У прямой есть вектор нормали с координатами \((A, B)\) . Он перпендиуклярен прямой, а в случае с полуплоскостью \(Ax + By + C \geq 0\) будет указывать в сторону самой полуплоскости.

Чтобы найти расстояние от точки \((x_0, y_0)\) до прямой \(Ax + By + C = 0\) , можно воспользоваться следующей формулой:

Точка пересечения. По сути, найти точку пересечения двух прямых — это то же самое, что и найти точку, которая удовлетворяет обоим условиям их уравнений:

\[ \begin A_1 x + B_1 y + C_1 = 0 \\ A_2 x + B_2 y + C_2 = 0 \end \implies \begin -x = \frac \\ -x = \frac \end \implies \frac = \frac \implies y = — \frac \]

Аналогично, \(x = \frac\) (обратите внимание на знаки).

Заметим, что знаменатель может оказаться нулем. Это означает, что векторное произведение векторов нормали нулевое, а значит прямые параллельны (в частности, это могут быть совпадающие прямые). Этот случай нужно обрабатывать отдельно.

Как это кодить в C++

Небольшой ликбез по объектно-ориентированному программированию в C++. Создадим класс, который будет отвечать за все операции с точками. В C++ есть два способа это сделать: через struct и через class . Их основное отличие в том, что по умолчанию в class все поля приватные — к ним нет прямого доступа снаружи. Это нужно для дополнительной защиты, чтобы в крупных промышленных проектах никто случайно ничего не поломал, но на олимпиадах это не очень актуально.

Точка \(\simeq\) вектор. Будем считать точка и вектор это один и тот же объект, так как они оба — это просто пара чисел. Будем сопоставлять точке её радиус-вектор — вектор из начала координат, ведущий в эту точку. По принятой в математике и физике нотации, будем обозночать вектора как r . Вы можете обозвать их как point , pt , vec — как угодно.

Функция r внутри класса вызывается при инциализации объекта. Её называют конструктором, и её можно указывать разную для разных параметров. Здесь r() вернёт точку с неопределенными (какие оказались в памяти в тот момент) координатами, а r(x, y) вернет точку с координатами \((x, y)\) .

Операции над векторами

Давайте напишем функцию, которая принимает вектора и что-то с ними делает. Например, считает длину:

Операторы

В C++ можно перегружать почти все стандартные операторы, например, + , — , и т. д.

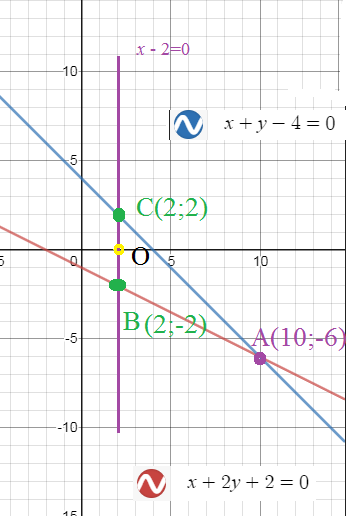
Задача 43087 уравнения двух сторон параллелограмма x.

Условие

уравнения двух сторон параллелограмма x + 2y + 2 = 0 и x + y-4= 0, а уравнения одной из его диагоналей x-2 = 0. Найти координаты вершин параллелограмма. Сделать рисунок. Прошу решите

Решение

[b](10;-6)[/b] — координата вершины А

Так как точка А не принадлежит диагонали x-2=0

то диагональ пересекается со сторонами x + 2y + 2 = 0 и x + y–4= 0

Середина ВС — точка О

Так как О- середина AD, то координаты точки D легко найти из формул середины отрезка DA

[b]D(-6;6)[/b]