Как записать дифференциальное уравнение изогнутой оси балки

Изогнутая ось балки

Изогнутая ось балки

Изгиб балки сопровождается искривлением ее оси. При этом точки оси получают поперечные перемещения или прогибы, а поперечные сечения поворачиваются относительно своих нейтральных осей. Углы поворота поперечных сечений принимаются равными углам наклона j касательной к изогнутой оси балки. Прогибы и углы поворота в балках часто называются линейными и угловыми перемещениями.

— закон изменения прогиба оси балки;

АМВ – изогнутая ось (упругая линия) – кривая, в которую превращается прямолинейная до деформации ось балки после приложения нагрузки;

— угол наклона касательной.

Прогибы и углы поворота в балках являются переменными величинами, т. е. функциями координаты х.

О знаке :

j — положительно, если при совмещении оси балки с касательной идет движение по часовой стрелке.

На часть конструкций часто накладываются жесткие ограничения на перемещения, например для балочных мостов, кран-балок и т. д., т. е. возникает необходимость рассмотрения геометрической стороны задачи при изгибе.

I . Дифференциальное уравнение изогнутой оси балки

Вид ИОБ определяется

1. действием нагрузки, которая вызывает внутренние усилия M , Q , N ;

2. геометрической характеристикой I ;

Значит

I – момент инерции поперечного сечения балки относительно его нейтральной оси;

Е – модуль упругости материала балки.

, E , I – от x не зависят.

В лекции «Напряжения в случае плоского поперечного изгиба балки» (прошлый семестр) рассматривалось «Определение нормальных напряжений». При этом было рассмотрено 3 стороны задачи:

1. геометрическая сторона задачи;

2. физическая сторона задачи;

3. статическая сторона задачи.

При рассмотрении геометрической стороны задачи была установлена зависимость

, где

— относительная деформация;

— прогиб оси балки;

— радиус кривизны ИОБ.

При рассмотрении физической стороны задачи была использована гипотеза о том, что продольные волокна балки не давят друг на друга, т. е. что изгиб сводится к деформациям продольных волокон, которые деформируются изолированно, испытывая простое одноосное растяжение (сжатие). Эта гипотеза делает возможным для связи деформаций и напряжений при изгибе использование закона Гука.

В статической стороне задачи было рассмотрено следующее сечение

Суммарное действие внутренних напряжений должно быть равно внешним воздействиям.

Имеет место 2 условия равновесия:

1.

2.

— сила по элементарным площадкам;

— сила по всему сечению.

Отсюда (1),

— радиус кривизны ИОБ;

— жесткость балки при изгибе (изгибная жесткость).

Так как в выражение (1) вошли все 3 фактора M , E , I , то осталось выразить через y .

Для этого воспользуемся выражением из высшей математики

(2)

Приравниваем (1) и (2).

(3) точное дифференц. уравнение ИОБ

Так как в реальных конструкциях нормами проектирования допускаются сравнительно малые прогибы, а именно

, то ИОБ в реальности пологая.

Угол

Поскольку , а , то этим слагаемым в выражении (3) можно пренебречь.

(4)

Эта формула устанавливает зависимость между ,и 2-ой производной от прогиба.

Известно, что , когда момент, растягивая нижние волокна, обращает балку выпуклостью вниз.

Тогда из математики (вторая производная от функции отрицательна, если кривая обращена выпуклостью в положительную сторону оси y ).

Таким образом, при положительном изгибающем моменте, 2-ая производная должна быть отрицательной, следовательно в уравнении (4) удерживается знак «-» и формула имеет вид

(5) приближенное дифференц. уравнение ИОБ

Основные дифференциальные зависимости

Ранее известные зависимости:

(6)

,

(7)

Уравнения (7) позволяют, имея q , Q и M (а эти величины всегда возможно определить, построив эпюры в балках), получить значения y (прогиба) и j (угла поворота).

II . Методы решения дифференциальных уравнений ИОБ

Существует 3 метода решения дифференциальных уравнений ИОБ:

1. Метод непосредственного интегрирования

2. Метод начальных параметров

1. Метод непосредственного интегрирования

Метод непосредственного интегрирования заключается в непосредственном интегрировании уравнения (5).

(8)

Зная закон изменения можно определить y как функцию от x ().

Интегрирование ведется по участкам, для которых должны быть известны аналитические выражения изгибающих моментов .

В результате двукратного интегрирования на каждом участке появляются 2 произвольные постоянные С1 и С2.

Если балка разбивается на n участков, то постоянных интегрирования будет 2 × n .

Их определяют из

1. граничных условий (способов закрепления);

2. условий сопряжения участков.

1. Условия закрепления (граничные условия)

1) жесткое защемление

При Þ и

2) шарнирное опирание

При Þ и

При Þ и

Таким образом, с учетом граничных условий осталось неизвестных.

2. Условия сопряжения граничных участков

при Þ ,

Таким образом, всегда можно составить условия сопряжения и найти уравнение ИОБ.

Дифференциальное уравнение оси изогнутой балки

Имеем закон Гука при изгибе: , где r(х) — радиус кривизны изогнутой оси балки в сечении х, М(х) — изгибающий момент в том же сечении, EJ — жесткость балки. Из высшей математики известно: — дифференциальное уравнение изогнутой оси балки. — тангенс угла между осью х и касательной к изогнутой оси. Эта величина очень мала (прогибы балки малы) Þ ее квадратом пренебрегают и угол поворота сечения приравнивают тангенсу. Приближенное дифференциальное ур-ние изогнутой оси балки: . Если ось y направлена вверх, то знак (+). В некоторых вузах ось y направляется вниз Þ(—). Интегрируя дифф. уравнение, получаем: — ур-ние углов поворота, интегрируем второй раз: — получаем ур-ние прогибов.

ИЛИ
Для определения уравнения оси изогнутой балки воспользуемся законом Гука:

.

Выражение для кривизны некоторой кривой:

.

В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому (вторая производная от прогиба представляет собой кривизну изогнутой оси балки (уравнение изгиба) в рассматриваемом месте балки: .

Продифференцировав полученное уравнение дважды по z, получимдифференциальное уравнение оси изогнутой балки: .

ИНТЕГРИРОВАНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ ОСИ ИЗОГНУТОЙ БАЛКИ

Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.

Второе интегрирование дифференциального уравнения оси изогнутой балкиопределяет характер изменения изгибающего момента.

Третье интегрирование дифференциального уравнения оси изогнутой балкиопределяет характер изменения углов поворота поперечных сечений.

Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.

Постоянные интегрирования определяются из условий закрепления балки

10.Определение прогибов и углов поворотапоперечного сечения балки определяют с помощью универсального уравнения изогнутой оси балки (универсального уравнения упругой линии балки)

Формула (закон изменения) прогиба балки в сечении с координатой z и угол поворота сечения (рис. 7.15):

a и b – абсциссы точек приложения сосредоточенного момента M и сосредоточенной силы P, соответственно; c и d – координаты начала и конца участка, нагруженного распределенной нагрузкой.

В формулы входят только внешние усилия, которые расположены левее сечения, в котором определяются перемещения балки.

Если какая-нибудь нагрузка имеет противоположное указанному на рисунке 7.15 направление, то у соответствующих слагаемых в формулах прогибов и углов поворота сечений следует поменять знак на противоположный.

Прогиб и угол поворота балки в начале координат (начальные параметры) определяются из условий закрепления балки.

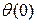
11.Косым изгибом называется вид нагружения, при котором плоскость действия изгибающего момента не проходит ни через одну из главных осей сечения.

Напряжения и перемещения при косом изгибе найдем, используя принцип независимости действия сил. Косой изгиб рассматривается при этом как одновременный изгиб в 2-х плоскостях zx и zy. Для этого изгибающий момент М_изг раскладывается на составляющие моменты осей х и у.

Нормальные напряжения в любой точке поперечного сечения могут быть вычислены как алгебраическая сумма напряжений, возникающих от моментов M_x и M_y:

a — угол отклонения плоскости действия M от вертикали.

Если в каждой точке сечения отложить по нормали вектор сигма, то концы векторов, как и при простом изгибе образуют плоскость. Уравнение нейтральной линии в сечении найдем, полагая сигма=0:

При косом изгибе нейтральная линия не перпендикулярна к плоскости изгибающего момента

14. Под кручением понимается такой вид нагружения, при котором в поперечных сечениях стержня возникает только крутящий момент. Прочие силовые факторы (изгибающие моменты, нормальная и поперечные силы) равны нулю.

Расчётная схема закрученного образца:

— полный угол закручивания.

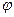
Берём элементарный участок:

— относительный угол поворота, приходящийся на единицу длины.

зависит от радиуса поперечного сечения круглого стержня.

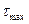
Внутренняя сила в точке К определяется

— полярный момент инерции поперечного сечения – геометрическая характеристика, зависящая от размеров поперечного сечения.

— зависимость при кручении.

15. Обобщённые силы и обобщенные перемещения

В механике мы различаем два самостоятельных силовых фактора — сосредоточенные силы Р, пару сил с моментом m (рис. 12.1, а). Иногда приходится иметь дело с группой сил и моментов. Назовём обобщённой силой Р группу сил или моментов, характеризуемых одним параметром или числом. На рис.12.1, б,в,г обобщёнными силами будут две силы Р, два момента m, распределённая нагрузка q.

А) б)

В) г)

Рис. 12.1

Производимая ими работа соответственно равна:

где а величина представляет собой площадь между исходной и изогнутой осями балки.

Обобщённым перемещениемназовём множители , стоящий в выражении работы при обобщённой силе и .

Таким образом, под обобщенной силой будем понимать любую нагрузку (сосредоточенные силы, сосредоточенные пары, распределенную линейную нагрузку, распределенную моментную нагрузку), а под обобщенным перемещением – тот вид перемещения, на котором обобщенная сила производит работу.

Обобщёнными силами могут быть не только внешние, но и внутренние:

Рассмотрим например статически неопределимую балку (рис. 12.2).

Рис. 12.2

Рассечём её на расстоянии z от левого конца и приложим к краям разреза по две нормальные силы N, две перерезывающие , два изгибающих момента , каждая из которых образует группу сил, характеризуемых одним числом, т.е. обобщённую силу.

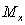
Возьмём две нормальные силы N. Они совершат работу:

Обобщённое перемещение представляет собой относительное расхождение краёв разреза. Аналогично можно рассмотреть две силы и два момента .

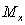
Обобщенные перемещения принято обозначать буквами или с двумя индексами. Первый индекс обозначает точку и направление перемещения, а второй указывает причину, вызвавшую искомое перемещение. Например, обозначает перемещение точки приложения силы F по направлению ее действия, вызванное этой же силой.

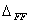
Для обозначения полного перемещения точки, вызванного несколькими обобщенными силами, при сохраняется только первый индекс.

Перемещение, вызванное безразмерной единичной силой или безразмерной единичной парой , обозначается символом и называется удельным. Потенциальная энергия бруса в общем случае нагружения.

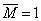
Общий случай нагружения бруса , когда в поперечных сечениях возникают нормальные и поперечные силы , изгибающие и крутящие моменты одновременно .

При разгрузке тела за счет потенциальной энергии производится работа.

Упругое тело является аккумулятором энергии.

Работа силы на упругом перемещении определяется половиной произведения наибольшего значения силы и перемещения ΔL .

Если бы между силой и перемещением не было прямой пропорциональности, вместо коэффициента ½ был бы получен какой –то другой коэффициент. В частности при постоянной силе он равен единице.

Исключая из полученного для U выражения ΔL, найдем

Энергия упругих деформаций стержня при изгибе определяется работой момента М на взаимном угловом перемещении dθ двух сечений.

Если нормальная сила N меняется вдоль оси стержня, то потенциальная энергия деформации должна определяться суммированием по участкам dz. Для элементарного участка dU = N 2 dz/2EF,а для всего стержня

Энергетическое соотношение широко используется при определении перемещения в сложных упругих системах.

17.Найдём работу которую совершают силы Р1 и Р2 в случайном приложении в различном порядке: А=1\2(Р1* ) +1\2(Р2 ;
А=1\2(Р2* ) +1\2(Р1 ; => Р2* А2=Р1* В1 — теорема Бетти
Работа первой силы на перемещение её точки приложено под действием второй силы равно работе второй силы на перемещение точки её приложения под действием первой силы.

18.Теорема Кастильяно не позволяет определить перемещения не в точках приложения сил. Если необходимо найти перемещение точки к которой не приложены внешние силы, то мы прикладываем в этой точке внешнюю силу Ф в инерциальное направление. Составим выражение для потенциальной энергии . Дальше по теореме Кастильяно находим производную получая соответственно . При этом считаем Ф=0. В поперечном сечении при приложении силы пропорциональной Ф. Будут возникать силовые факторы
Мк=Мкр+Мк1 * Ф где: Мкр — крутящий момент от заданной нагрузки; Мк1 — коэф. пропорц.
где где — искомое перемещение (линейное или угловое);

Мp, М1 — аналитические выражения изгибающих моментов соответственно от заданной и единичной cилы;

EJх — жесткость сечения балки в плоскости изгиба.

19. При вычислении интегралов вместо аналитических выражений моментов используются их эпюры. Т.е. значение можно найти по способу Верещагина, «перемножив» эпюры Мp и М1.

Перемножить две эпюры — значит площадь нелинейной эпюры изгибающих моментов умножить на ординату другой обязательно линейной эпюры, находящейся под центром тяжести первой, и результат разделить на жесткость (в случаях, когда на данном участке обе эпюры линейны, совершенно безразлично, на какой из них брать площадь, а на какой ординату).

где Ω — площадь произвольной фигуры; Мc — ордината прямолинейной эпюры, соответствующей центру тяжести площади Ω

20.Статично невизначені стержневі системи. Вибір основної системи: Под стержневой системою понимают конструкцію елементами которой является стержень. В случае если стержени работают на растяжение сжатие то такая конструкція називается фермой, если стержни работают на кручение или изгиб то такая конструкція називается рамой.Статически определимой системой називают системи в которих число ур. Равновесия равно числу неизвестних реакций связи, если число неизвестних реакцій свіязей більше числа ур. Равновесия то такая система назив.статически неопределимой, при етом разность между етими числами назив. степеню неопределимости системи.

22.Нерозрізні балки.Рівняння трьох моментів.Способ раскрития статической неопределимости основан на врезании дополнительних шарниров что как известно приводит к снижению статической неопределимости на число равное числу дополнительних шарниров.Число дополнительних условий также равно числу дополнительних шарниров. Теорема о 3 моментахпредпологает что дополнительние шарніри врезаются на лишних опорах, получим соотношение для неизвестних моментов которие возникают в данном случае этих дополнительних шарнірах:

Дифференциальное уравнение оси изогнутой балки

Для определения уравнения оси изогнутой балки воспользуемся законом Гука:

.

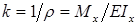
Выражение для кривизны некоторой кривой:

.

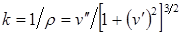
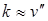
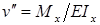
В пределах упругих деформаций квадрат угла поворота поперечного сечения балки ничтожно мал по сравнению с единицей. Поэтому (вторая производная от прогиба представляет собой кривизну изогнутой оси балки ( уравнение изгиба ) в рассматриваемом месте балки:.

Продифференцировав полученное уравнение дважды по z, получим дифференциальное уравнение оси изогнутой балки : .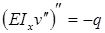

Интегрирование дифференциального уравнения оси изогнутой балки

Интегрируя дифференциальное уравнение оси изогнутой балки первый раз, получим выражение, дающее закон изменения поперечной силы по длине балки.

Второе интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения изгибающего момента.

Третье интегрирование дифференциального уравнения оси изогнутой балки определяет характер изменения углов поворота поперечных сечений.

Четвертое интегрирование дифференциального уравнения оси изогнутой балки определяет закон изменения прогибов балки по ее длине.

Постоянные интегрирования определяются из условий закрепления балки.