Как записать характеристическое уравнение сау

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

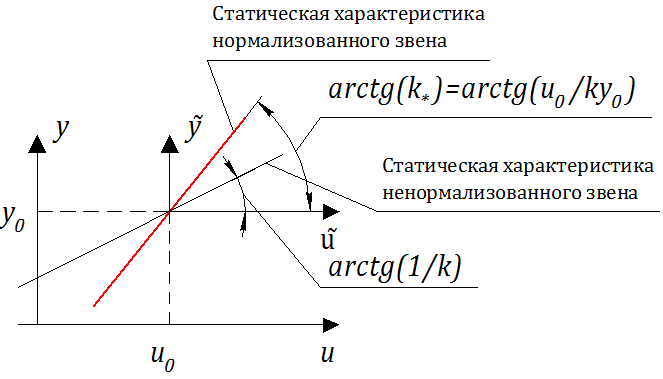
На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

1. Нелинейностью статической характеристики.
2. Нелинейностью динамических членов в уравнениях динамики.
3. Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

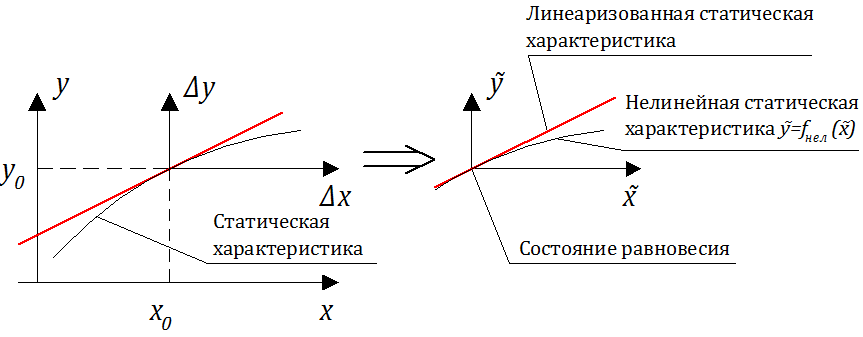
• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

1. Перейдем к безразмерным переменным (нормализованным);
2. Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_<част.>(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

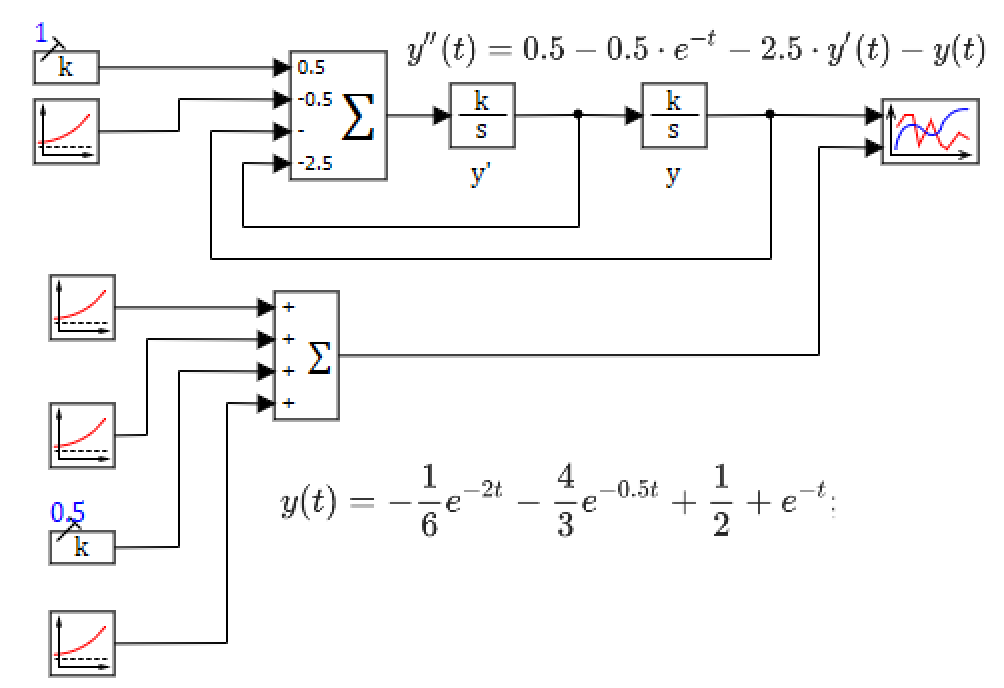
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

Как записать характеристическое уравнение сау

Это графоаналитические методы, позволяющие по виду частотных характеристик САУ судить об их устойчивости. Их общее достоинство в простой геометрической интерпретации, наглядности и в отсутствии ограничений на порядок дифференциального уравнения.

9.1. Принцип аргумента

Запишем характеристический полином САУ в виде

D(p) = a ₀ (p — p ₁ )(p — p ₂ ). (p — p _n ) = 0.

p _i = _i + ji = |p _i |e jarg(pi) ,

где arg(p _i ) = arctg(i/a _i ) + k,

.

Каждый корень можно изобразить вектором на комплексной плоскости (рис.68а), тогда разность p — p _i изобразится разностью векторов (рис.68б), где p — любое число.

Еcли менять значение p произвольным образом, то конец вектора p — p _i будет перемещаться по комплексно плоскости, а его начало будет оставаться неподвижным, так как p _i — это конкретное неизменное значение.

В частном случае, если на вход системы подавать гармонические колебания с различной частотой , то p = j , а характеристический полином принимает вид:

D(j) = a ₀ (j — p ₁ )(j — p ₂ ). (j — p _n ).

При этом концы векторов j — p _i будут находиться на мнимой оси (рис.68в). Если менять от — до + , то каждый вектор j — p _i будет поворачиваться относительно своего начала p _i на угол +p для левых и — p для правых корней (рис.68г).

Характеристический полином можно представить в виде

D(j) = |D(j)|e jarg(D(j) ) ,

где |D(j)| = a ₀ |j — p ₁ | |j — p ₂ |. |j — p _n |,

arg(D(j)) = arg(j — p ₁ ) + arg(j — p ₂ ) + .. + arg(j — p _n ).

Пусть из n корней m — правые, а n — m — левые, тогда угол поворота вектора D(j) при изменении от — до + равен

= (n — m) — m,

или при изменении от 0 до + получаем

= (n — 2m) (/2).

Отсюда вытекает правило: изменение аргумента вектора b при изменении частоты от — до + равно разности между числом левых и правых корней уравнения D(p) = 0 , умноженному на , а при изменении частоты от 0 до + эта разность умножается на /2 .

Это и есть принцип аргумента . Он положен в основе всех частотных критериев устойчивости. Мы рассмотрим два наиболее распространенных критерия: критерий Михайлова и критерий Найквиста.

9.2. Критерий устойчивости Михайлова

Так как для устойчивой САУ число правых корней m = 0 , то угол поворота вектора D(j) составит

= n/2 .

То есть САУ будет устойчива, если вектор D(j) при изменении частоты от 0 до + повернется на угол n/2 .

При этом конец вектора опишет кривую, называемую годографом Михайлова . Она начинается на положительной полуоси, так как D(0) = a _n , и последовательно проходит против часовой стрелки n квадрантов комплексной плоскости, уход в бесконечность в n — ом квадранте (рис.69а).

Если это правило нарушается (например, число проходимых кривой квадрантов не равно n , или нарушается последовательность прохождения квадрантов (рис.69б)), то такая САУ неустойчива — это и есть необходимое и достаточное условие критерия Михайлова .

Достоинства . Этот критерий удобен своей наглядностью. Так, если кривая проходит вблизи начала координат, то САУ находится вблизи границы устойчивости и наоборот. Этим критерием удобно пользоваться, если известно уравнение замкнутой САУ.

Для облегчения построения годографа Михайлова выражение для D(j) представляют суммой вещественной и мнимой составляющих:

D(j) = a ₀ (j — p ₁ )(j — p ₂ ). (j — p _n ) = a ₀ (j) n + a ₁ (j) n — 1 + . + a _n = ReD(j) + jImD(j),

ReD(j) = a _n — a _{n — 2} 2 + a _{n- 4} 4 — .

ImD(j) = a _{n — 1} — a _{n — 3} 3 + a _{n- 5} 5 — .

Меняя от 0 до по этим формулам находят координаты точек годографа, которые соединяют плавной линией.

9.3. Критерий устойчивости Найквиста

Этот критерий позволяет судить об устойчивости замкнутой САУ по виду АФЧХ разомкнутой САУ (рис.70). Исследование разомкнутой САУ проще, чем замкнутой. Его можно производить экспериментально, поэтому часто оказывается, что АФЧХ разомкнутой САУ мы имеем или можем получить.

Передаточная функция разомкнутой САУ:

W _p (p) = W p (p)/D p (p) = > уравнение динамики: y(t) = e(t) ,

D p (p)y(t) = K p (p)e(t).

Здесь D p (p) — характеристический полином разомкнутой САУ. То есть по виду корней уравнения D p (p) = 0 можно судить об устойчивости разомкнутой САУ. Но это пока ничего не говорит об устойчивости замкнутой САУ.

Для того, чтобы получить уравнение динамики замкнутой САУ при свободном движении, считаем, что внешнее воздействие u = 0 , тогда на вход первого звена САУ подается сигнал

e(t) = u(t) — y(t) = — y(t).

D p (p)y(t) = K p (p)( — y(t)),

следовательно уравнение замкнутой САУ:

(D p (p) + K p (p))y(t) = 0.

Таким образом, характеристическое уравнение замкнутой САУ:

D_з(p) = D p (p) + K p (p) = 0.

По виду его корней уже можно судить об устойчивости замкнутой САУ.

Воспользуемся вспомогательной функцией:

F(j) = 1 + W _р (j) = .

По сути дела она представляет собой АФЧХ разомкнутой САУ, сдвинутую на единицу вправо. Степени полиномов D з (j) и D p (j) равны n. Эти полиномы имеют свои корни p_зi и p _pi , то есть можно записать:

F(jw) = .

Каждую разность в скобках можно представить вектором на комплексной плоскости, конец которого скользит по мнимой оси (рис.63в). При изменении от — до + каждый из векторов j — p _i будет поворачиваться на угол +p , если корень левый и -p , если корень правый.

Пусть полином Dз(jw) имеет m правых корней и n — m левых, а полином D p (j) имеет g правых корней и n — g левых. Тогда суммарный угол поворота вектора функции F(j) при изменении частоты от — до + :

p[(n — m) — m)] — p[(n — g) — g] = 2p(g — m).

Если замкнутая САУ устойчива, то m = 0 , тогда суммарный поворот вектора F(j) при изменении от — до + должен быть равен 2g , а при изменении от 0 до + он составит 2g/2 .

Отсюда можно сформулировать критерий устойчивости Найквиста : если разомкнутая САУ неустойчива и имеет g правых корней, то для того, чтобы замкнутая САУ была устойчива необходимо и достаточно, чтобы вектор F(j) при изменении от 0 до + охватывал начало координат в положительном направлении g/2 раз, то есть АФЧХ разомкнутой САУ должна охватвать g/2 раз точку ( — 1, j0) .

На рис.71а приведены АФЧХ разомкнутых САУ, устойчивых в замкнутом состоянии, на рис.71б — замкнутая САУ неустойчива.

На рис.71в и 71г показаны АФЧХ разомкнутых астатических САУ, соответственно устойчивых и неустойчивых в замкнутом состоянии. Их особенность в том, что АФЧХ при 0 уходит в бесконечность.

В этом случае при использовании критерия Найквиста ее мысленно замыкают на вещественную ось по дуге окружности бесконечно большого радиуса.

Достоинство . Критерий Найквиста очень нагляден. Он позволяет не только выявить, устойчива ли САУ, но и, в случае, если она неустойчива, наметить меры по достижению устойчивости.

1. Что называется частотными критериями устойчивости САУ?
2. В чем преимущество частотных критериев устойчивости перед алгебраическими:
3. Сформулируйте принцип аргумента.
4. Сформулируйте критерий устойчивости Михайлова.
5. Поясните каждый из годографов на рис.69. Как вы судите об устойчивости соответствующих САУ?
6. Как из годографов на рис.69 соответствуют САУ, находящимся на границе устойчивости?
7. Сформулируйте критерий устойчивости Найквиста.
8. Поясните, являются ли устойчивыми САУ, АФЧХ которых в разомкнутом состоянии представлены на рис.71. Почему?
9. В чем особенность использования критерия Найквиста для астатических САУ?
10. Как из годографов на рис.71 соответствуют САУ, находящимся на границе устойчивости?

Анализ основных свойств линейных САУ

2.4.1 Анализ устойчивости САУ

2.4.1.1 Основные понятия

Устойчивость – это свойство системы возвращаться в исходный или близкий к нему установившийся режим после всякого выхода из него в результате какого-либо возмущающего воздействия.

На рисунках 2.37 и 2.38 показаны типичные кривые переходных процессов соответственно в неустойчивой и устойчивой системах. Если система неустойчива, то достаточно любого возмущающего воздействия, чтобы в ней начался расходящийся процесс ухода из исходного установившегося состояния. Этот процесс может быть апериодическим (кривая 1) или колебательным (кривая 2). В случае устойчивой системы (рисунок 2.38) переходный процесс, вызванный возмущающим воздействием, со временем затухает апериодически (кривая 1) или колебательно (кривая 2), и система вновь возвращается в исходное установившееся состояние. Таким образом, устойчивую систему можно определить как систему, переходные процессы в которой являются затухающими.

Оценка устойчивости есть оценка принципиальной способности осуществлять регулирование, поэтому с оценки устойчивости и начинают исследование всякой САУ. Появление неустойчивости при желаемом изменении какого-либо параметра системы (например, при увеличении передаточного коэффициента) часто ограничивает возможности повышения качества регулирования.

Об устойчивости САУ судят по решению ее дифференциального уравнения (2.5), которое можно записать в виде

где yуст(t) – частное решение неоднородного дифференциального уравнения (2.5), описывающее вынужденный режим системы, устанавливающийся после окончания переходного процесса;

yп(t) – общее решение однородного дифференциального уравнения, описывающее переходный процесс в САУ, вызванный управляющим (задающим) или возмущающим воздействием.

Иногда yуст(t) и yп(t) называют соответственно вынужденной и переходной составляющими.

САУ называют устойчивой, если с течением времени переходная составляющая стремится к нулю, т.е. yп(t) ® 0 при t ® ¥. Переходную составляющую yп(t) находят решением характеристического уравнения системы и записывают в следующем виде:

, (2.107)

где Ci – постоянные интегрирования, определяющиеся НУ;

pi – корни характеристического уравнения (2.7). Их называют также полюсами основной ПФ системы управления F(s).

Таким образом, переходный процесс описывают суммой составляющих, количество которых определяется количеством корней piхарактеристического уравнения, т.е. порядком уравнения САУ.

Корни характеристического уравнения определяются только видом самого уравнения, т.е. только видом левой части ДУ системы (2.5). Постоянные интегрирования определяются также и правой частью ДУ системы (2.5). В связи с этим скорость затухания и форма переходного процесса определяются как левой, так и правой частями исходного ДУ. Однако для оценки устойчивости САУ достаточно установить факт затухания переходного процесса. При этом скорость затухания и форма переходного процесса значения не имеют. Поэтому устойчивость линейной САУ не зависит от вида правой части ДУ системы (2.5) и определяется только характеристическим уравнением (2.7). Более того, для оценки устойчивости САУ нет необходимости решать характеристическое уравнение и вычислять его корни. Достаточно определить основные свойства корней.

В общем случае корни piявляются комплексными. При этом они образуют пары сопряженных корней: pi, i+1= ai± jbi, где aiможет быть положительным или отрицательным числом. Каждая такая пара корней дает в выражении (2.107) составляющую переходного процесса вида

,

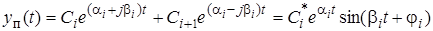
представляющую собой синусоиду с амплитудой, изменяющейся во времени по экспоненте. При этом, если ai 0 колебания будут расходящимися (кривая 2 на рисунке 2.37). В частном случае, когда bi = 0, характеристическое уравнение имеет действительный корень pi = ai. Соответствующая ему составляющая переходного процесса 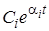изменяется по экспоненциальному закону, затухая или увеличиваясь (кривая 1 на рисунке 2.37) в зависимости от знака ai.

Итак, в общем случае переходный процесс САУ состоит из колебательных и апериодических составляющих. Общим условием затухания всех составляющих, а значит, и всего переходного процесса в целом является отрицательный знак действительных частей всех корней характеристического уравнения САУ, т.е. всех полюсов (нулей знаменателя) ее ПФ. Если хотя бы один корень имеет положительную действительную часть, он даст расходящуюся составляющую переходного процесса и система будет неустойчивой. Наличие пары сопряженных чисто мнимых корней pi, i+1 = ± jbiдаст незатухающую гармоническую составляющую переходного процесса. При этом в САУ устанавливаются незатухающие колебания с частотой bi. Этот случай является граничным между устойчивостью и неустойчивостью – САУ при этом находится на границе устойчивости.

При изображении корней характеристического уравнения на комплексной плоскости (рисунок 2.3) условие устойчивости линейной САУ формулируют так: условием устойчивости САУ является расположение всех корней ее характеристического уравнения, т.е. полюсов ПФ системы, в левой комплексной полуплоскости или, короче, все корни должны быть «левыми».

Таким образом, мнимая ось представляет собой граничную линию в плоскости корней, за которой не должны находиться корни характеристического уравнения. Вся левая полуплоскость представляет собой при этом область устойчивости. В связи с этим мнимую ось называют границей устойчивости. Теоретически САУ может находиться на границе устойчивости при наличии:

1) нулевого корня;

2) пары сопряженных мнимых корней;

3) бесконечно большого корня.

Остальные корни должны иметь отрицательные действительные части.

Принципиальная особенность оценки устойчивости реальной САУ заключается в том, что при этом исследуется линейная математическая модель системы. Так как ни одна реальная САУ не является строго линейной, линейную ММ получают линеаризацией реальных характеристик и уравнений САУ (см. п. 2.1.1.5). При разложении в ряд Тейлора удерживают в уравнении линейные члены и отбрасывают члены высших порядков, которые для малых отклонений считают пренебрежимо малыми. Полученные линеаризованные уравнения называют уравнениями первого приближения. Принципиальная возможность оценки устойчивости реальной (нелинейной) САУ по уравнениям первого приближения доказана А.М.Ляпуновым, сформулировавшим условия устойчивости в следующих теоремах:

1) если характеристическое уравнение линеаризованной САУ имеет все корни с отрицательными вещественными частями, то реальная система будет также устойчива, т.е. малые нелинейные члены не могут в этом случае нарушить устойчивость САУ;

2) если характеристическое уравнение линеаризованной САУ имеет хотя бы один корень с положительной вещественной частью, то реальная система будет также неустойчивой, т.е. малые нелинейные члены не могут сделать ее устойчивой;

3) при наличии нулевых и чисто мнимых корней поведение реальной САУ не всегда даже качественно определяется ее линеаризованными уравнениями. При этом даже малые нелинейные члены могут коренным образом изменить свойства системы, сделав САУ устойчивой или неустойчивой.

Третий случай для линейной ТАУ не представляет практического интереса, так как определяет поведение системы на границе устойчивости. Работоспособная САУ не должна находиться даже вблизи от границы устойчивости.

Поэтому для оценки устойчивости САУ достаточно первых двух теорем, которые являются обоснованием теории устойчивости линеаризованных систем управления, основанной на требованиях к корням характеристического уравнения.

Однако для суждения об устойчивости САУ не требуется находить корни ее характеристического уравнения в связи с тем, что разработаны косвенные признаки, по которым судят о знаке действительных частей этих корней и тем самым об устойчивости САУ, не решая самого характеристического уравнения. Эти косвенные признаки называют критериями устойчивости.

Критерии устойчивости разделяют на алгебраические и частотные. К алгебраическим относят критерии Гурвица, Льенара-Шипара и Рауса, к частотным – критерии Михайлова и Найквиста.

2.4.1.2 Критерий устойчивости Рауса-Гурвица

Из алгебраических критериев устойчивости САУ наибольшее распространение получили критерии устойчивости Рауса и Гурвица. Критерий Гурвица часто называют критерием Рауса-Гурвица, так как он может быть получен из критерия Рауса.

Методика исследования устойчивости САУ по критерию Рауса-Гурвица сводится к следующему. Предварительно определяют характеристический полином замкнутой САУ (2.8):

.

При этом коэффициент anдолжен быть положительным (an > 0). Затем составляют главный определитель Гурвица размером [n ´ n].

Диагональными элементами этого определителя являются коэффициенты характеристического полинома, расположенные в порядке убывания индексов от an-1до a0. Каждую строку определителя Dnзаполняют коэффициентами полинома D(s) с убывающими индексами слева направо так, чтобы чередовались строки с нечетными и четными индексами. Концы строк дополняют нулями так, чтобы главный определитель имел n столбцов. Третью и четвертую строки получают сдвигом первых двух строк на один элемент вправо и т.д.

После этого, отчеркивая в главном определителе Гурвица, как показано пунктиром, диагональные миноры, получают определители Гурвица низшего порядка:

и т.д.

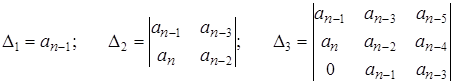
Критерии устойчивости Рауса-Гурвица формулируют следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы все определители Гурвица были положительны. Таким образом, САУ устойчива, если an > 0 при выполнении следующих условий:

D1 > 0; D2 > 0; D3 > 0; …, Dn > 0.

Раскрыв определители Гурвица, получают условия устойчивости, которые для САУ первого – пятого порядков представлены в таблице 2.9.

Таблица 2.9 – Условия устойчивости САУ
Характеристическое уравнение САУ	Условия устойчивости САУ
	,

Для уравнений первой и второй степеней необходимый критерий устойчивости, заключающийся в требовании положительности всех коэффициентов характеристического уравнения, является и достаточным. Для уравнений более высокого порядка положительность коэффициентов характеристического уравнения является необходимым, но недостаточ­ным условием устойчивости. Например, необходимые и достаточные условия устойчивости для уравнения третьей степени включают кроме требования положительности четырех коэффициентов характеристичес­кого уравнения дополнительное пятое условие . Условия устойчивости усложняются с ростом порядка системы.

2.4.1.3 Критерий устойчивости Михайлова

Критерий устойчивости Михайлова принадлежит к числу частотных критериев и позволяет оценивать устойчивость замкнутой САУ по виду годографа, который может быть получен с помощью характеристического уравнения. Годограф Михайлова описывается концом вектора D(jw) на комплексной плоскости при изменении частоты w от 0 до ¥. Вектор D(jw) получают из характеристического полинома замкнутой САУ D(s) при подстановке в последний s = jw:

. (2.108)

Полученное выражение является функцией комплексного аргумента jw. По аналогии с АФЧХ динамического звена в соответствии с (2.55) названную функцию целесообразно привести к алгебраическому виду

где ; .

Алгебраическая форма функции по сравнению с показательной формой позволяет построить годограф Михайлова D(jw) существенно проще. По формулам X(w) и Y(w) вычисляют координаты точек годографа, по которым затем наносят точки на комплексную плоскость. Соединяя точки непрерывной линией, получают искомый годограф Михайлова D(jw) САУ (см. рисунок 2.39).

Годограф Михайлова D(jw) начинается на действительной положительной полуоси в точке a0(w = 0) и при w®¥ уходит в бесконеч­ность в соответствующем квадранте. Годограф Михайлова устойчивых САУ всегда имеет плавную спирале­видную форму.

Критерий Михайлова формули­руют следующим образом: для устойчивости САУ необходимо и достаточно, чтобы годограф Михайлова обошел в положительном направлении (против часовой стрелки) последовательно n квадрантов, нигде не обращаясь в нуль.

Приблизительный вид годографов Михайлова устойчивых САУ 1-го – 5-го порядков показан на рисунке 2.39. Принято для удобства сравнения различных САУ равенство свободных членов a0их ДУ.

Признаком неустойчивости САУ является нарушение количества и последовательности пройденных годографом Михайлова квадрантов комплексной плоскости.

Если САУ находится на границе устойчивости, то годограф проходит через начало координат (пунктирная кривая на рисунке 2.39).

2.4.1.4 Критерий устойчивости Найквиста

Критерий Найквиста позволяет судить об устойчивости замкнутой САУ по АФЧХ разомкнутой системы W(jw). Годограф W(jw) получают аналитически или экспериментально. В зависимости от свойств разомкнутой САУ годограф может иметь различный вид. В связи с этим при анализе устойчивости замкнутой САУ различают три типовых случая состояния (устойчивости) разомкнутой САУ.

Первый случай охватывает САУ, устойчивые в разомкнутом состоянии. Таким свойством обладают статические САУ, ПФ которых в общем случае имеют вид оператора (2.38), а годограф W(jw) совместно с осью вещественных чисел образует замкнутый контур (см. рисунки 2.40 и 2.41). Начинается (w = 0) годограф на вещественной положительной полуоси в точке с координатами (K, j0), где K – коэффициент передачи (усиления) разомкнутой САУ, а заканчивается в начале координат (w = ¥).

В первом случае для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ не охватывал точку с координатами (-1; 0j), которую называют критической. Годограф 1 на рисунке 2.40 принадлежит устойчивой САУ, 2 – неустойчивой, 3 – САУ, находящейся на границе устойчивости. На рисунке 2.41 показан годограф W(jw) устойчивой САУ, имеющий вид клювообразной кривой. Этот годограф пересекает отрицательную действительную полуось левее критической точки. При этом количество положительных (сверху вниз) переходов годографа через полуось левее критической точки равно количеству отрицательных (снизу вверх) переходов. Это означает, что годограф действительно не охватывает критическую точку. На рисунке 2.41 отрицательный и положительный переходы отмечены знаками «-» и «+».

Второй случай охватывает нейтральные САУ, т.е. находящиеся в разомкнутом состоянии на границе устойчивости. Таким свойством обладают астатические САУ, ПФ которых в общем случае имеют вид оператора (2.39), а годограф W(jw) не может образовать замкнутого контура ни с одной из осей, так как начинается (w = 0) в бесконечности. Эту особенность называют разрывом годографа.

Во втором случае критерий Найквиста формулируется следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ, дополненный на участке разрыва дугой бесконечно большого радиуса, не охватывал критическую точку.

На рисунке 2.42 показаны годографы 1 и 2 САУ с астатизмом первого порядка (v = 1). Годограф 1 принадлежит устойчивой, а годограф 2 – неустойчивой системе.

Клювообразный годограф на ри­сунке 2.43 принадлежит устойчивой САУ с астатизмом второго порядка (v = 2).

Третий случай охватывает САУ, неустойчивые в разомкнутом состоя­нии. Характеристический полином таких систем A(s) имеет l «правых» корней, т.е. корней с положительной вещественной частью.

В третьем случае, наиболее общем, критерий Найквиста формулируется следующим образом: для устойчивости замкнутой САУ необходимо и достаточно, чтобы годограф разомкнутой САУ охватывал критическую точку l/2 раз в положительном направлении (против часовой стрелки).

Анализ устойчивости САУ с годографом сложной формы, например изобра­женным на рисунке 2.43, упрощается при использова­нии правила переходов. Критерий Найквиста форму­лируется при этом следую­щим образом: замкнутая САУ устойчива, если раз­ность между количеством положительных и отрица­тельных переходов годогра­фа разомкнутой системы W(jw) через отрезок вещественной оси от -¥ до критической точки равна l/2. Годограф может начинаться на указанном отрезке при w = 0 (рисунок 2.43) или заканчиваться при w = ¥. В этом случае считают, что годограф совершает полперехода. Так, например, годограф, изображенный на рисунке 2.43, совершает один положительный переход, отмеченный знаком «+», и половину отрицательного перехода, отмеченного знаком «-«. Разность названных переходов равна +1/2. Замкнутая САУ будет устойчивой, если l/2 = 1/2.

Если характеристический полином разомкнутой системы A(s) кроме корней с вещественной частью имеет нулевые и чисто мнимые корни, то на участках разрыва годограф W(jw) должен быть дополнен дугой бесконечно большого радиуса.

Для определения устойчивости САУ по критерию Найквиста используют не только АФЧХ (годограф), но ЛАЧХ и ЛФЧХ разомкнутой системы.

Формулировка критерия Найквиста при этом следующая: для устойчивости замкнутой САУ необходимо и достаточно, чтобы разность между количеством положительных и отрицательных переходов ЛФЧХ через линии с ординатами -p, -3p и т.д. равнялась l/2. Пересечение ЛФЧХ линии -p снизу вверх считают положительным, а сверху вниз – отрицательным. Более просто определяется устойчивость замкнутых САУ , которые в разомкнутом состоянии устойчивы или нейтральны. Критерий Найквиста формулируется следующим образом: замкнутая система будет устойчива, если количество переходов ЛФЧХ через линию -p при положительных значениях ЛАЧХ (L(w) > 0) будет четным или равным нулю.

Этот признак иногда называют логарифмическим критерием устойчивости.

В качестве примера на рисунке 2.44 изображены логарифмические ЧХ трех систем, которые отличаются видом ЛФЧХ j(w), но при этом имеют одинаковую ЛАЧХ L(w). Анализ характеристик по логарифмическому критерию показывает, что устойчивой является первая САУ. ЛФЧХ этой системы (кривая 1 на рисунке 2.44) при положительных значениях ЛАЧХ (L(w) > 0) не пересекает линии с ординатой -180°, т.е. количество переходов рано нулю. Напротив, ЛФЧХ третьей САУ (кривая 3 на рисунке 2.44) один раз пересекает линию с ординатой -180°. Следовательно, эта САУ является неустойчивой.

2.4.1.5 Оценка запаса устойчивости САУ

При оценке устойчивости САУ одного факта устойчивости недостаточно, необходимо еще оценить запас устойчивости, т.е. степень удаленности САУ от границы устойчивости. Запас устойчивости должен гарантировать устойчивость реальной системы по установленному факту устойчивости ее модели. Известно, что линеаризация ММ и погрешность определения ее параметров, а также нестабильность параметров САУ в процессе эксплуатации оказывают существенное влияние на устойчи­вость реальной САУ. Запас устойчивости «покрывает» действие указанных причин.

О запасе устойчивости можно судить по расположению корней характеристического уравнения САУ в левой части комплексной плоскости (рисунок 2.3): чем дальше отстоят они от оси мнимых чисел, тем больше запас устойчивости.

Каждый критерий устойчивости позволяет определять запас устойчивости. Количественная оценка запаса устойчивости зависит от того, какой критерий устойчивости выбран.

Наибольшее распространение получила методика оценки запаса устойчивости САУ по критерию Найквиста разомкнутой системы. В качестве меры запаса устойчивости приняты вытекающие из критерия Найквиста две величины – запас устойчивости по фазе и запас устойчивости по амплитуде . Эти величины показаны на рисунке 2.44 на примере устойчивой САУ.

Запас устойчивости по фазе определяется величиной , на которую должно возрасти запаздывание по фазе САУ на частоте среза wср, чтобы САУ оказалась на границе устойчивости.

Запас устойчивости по амплитуде определяется величиной амплитуды допустимого подъема ЛАЧХ, при котором САУ окажется на границе устойчивости. Таким образом, запас устойчивости по амплитуде представляет собой запас по коэффициенту передачи К разомкнутой САУ по отношению к его критическому по устойчивости значению.

При проектировании САУ рекомен­дуется выбирать и . Последнее соответствует, примерно, двой­ному запасу коэффициента передачи.

Оценить запас устойчивости замкну­той САУ можно также по АФЧХ разомкнутой САУ W(jw) (рисунок 2.45).

Совместно с названным годографом на комплексной плоскости проводят окружность с центром в начале координат. Годограф и окружность пересекаются на частоте среза в точке D1, угловое положение которой характеризует запас устойчивости по фазе Dj.

Запас устойчивости по амплитуде характеризуется положением на вещественной оси точки D2:

. (2.109)

2.4.1.6 Понятие об области устойчивости САУ

При синтезе САУ, когда требуется определить влияние каких-либо варьируемых параметров на устойчивость, строят область устойчивости системы в пространстве этих варьируемых параметров. Область устойчи­­вости определяет совокупность значений параметров САУ, при которых система устойчива.

В случае двух варьируемых параметров область устойчивости изображается на плоскости А0В (рисунок 2.46).

При трех варьируемых параметрах область устойчивости получается трехмерной и т.д. Варьируемыми параметрами (например, А и B) могут быть постоянные времени, коэффициент передачи и их любые комбинации. Граница устойчивости изображается линией, кото­рая может быть замкнутой (рисунок 2.46) и разомкнутой. Каждая точка Fi внутри области устойчивости определяет комбина­цию варьируемых параметров Aiи Bi, при которых САУ устойчива.

Если САУ в пространстве всех своих параметров не имеет области устойчивости, то ее называют структурно неустойчивой. Такая САУ не может быть сделана устойчивой путем изменения (настройки) ее параметров. Для достижения устойчивости в этом случае необходимо изменить структурную схему САУ.

Уравнение границ области устойчивости можно находить, пользуясь любым критерием устойчивости. Однако чаще всего на практике применяют метод D-разбиения /6, 14, 15/.

2.4.2 Анализ инвариантности САУ

В ТАУ под инвариантностью САУ понимают независимость управляемой (выходной) величины САУ y(t) от одного или нескольких возмущений z1 – z3(рисунок 1.3) и независимость рассогласования e(t) следящей системы от управляющего (задающего) воздействия g(t).

В простейшем случае инвариантности САУ достигают посредством принципа управления по возмущению (см. п. 1.2.3). При этом управляющее устройство (УУ на рисунке 1.3), которое называют компенсатором, под влиянием возмущения z(t) воздействует на ОУ. В результате этого непосредственное (естественное) влияние возмущения z(t) на управляемую величину y(t) уравновешивается (компенсируется). Единственная цель управления при этом состоит в устранении влияния одного, заранее выбранного возмущения. Компенсируют только одно возмущение, однако возможна полная компенсация. Компенсатор для этого должен иметь по крайней мере измерительное устройство (ИУ) для измерения возмущения z(t) и исполнительный механизм (ИМ) для создания необходимого воздействия yр(t) на ОУ (рисунок 2.47). Таким образом, компенсация возмущения достигается специальной структурой САУ (структурная компенсация возмущения). Кроме того, система управления должна удовлетворять условию инвариантности. Структур­ный признак реализуемости условия инвариантности сформулирован Б.Н.Петровым в форме признака двухканальности: в динамической системе должно быть по крайней мере два канала воздействия возмущения на координату (управляемую величину), инвариантность которой от этого возмущения должна быть обеспечена. Только в этом случае воздействие возмущения по одному каналу (пунктирная линия 1 на рисунке 2.47) может быть компенсировано противоположным по знаку воздействием этого же возмущения по другому каналу (пунктирная линия 2). Принцип двухканальности – это необходимый, но недостаточный критерий реализуемости условия инвариантности. Достаточным критерием реализуемости условия инвариантности считают возможность физической осуществимости необходимых для этого реальных элементов (устройств) САУ.

Трудности реализации условия инвариантности обусловили целесообразность создания САУ и с приближенным его удовлетворением. Поэтому в зависимости от степени реализации условия инвариантности и получаемых результатов различают следующие виды инвариантности:

2) полную с точностью до переходной составляющей;

3) частичную до l-й производной включительно;

4) частичную с точностью до малой величины e.

Под абсолютной инвариантностью регулируемой величины понимают совершенную независимость ее от возмущения, момента приложения возмущения к САУ и его последующего изменения.

Если от возмущения не зависит лишь установившееся значение регулируемой величины, то говорят о полной инвариантности. В этом случае начальные значения возмущения и его производных обусловливают переходную составляющую регулируемой величины.

Под частичной инвариантностью понимают независимость регулируемой величины в установившемся режиме лишь от абсолютного значения возмущения и его младших производных до l-й включительно. Причина названной «частичности» заключается в физической нереализуемости элементов САУ, необходимых для обеспечения условия инвариантности.

Вследствие неизбежных неточностей возможно только приближение к абсолютной, полной или частичной инвариантности. Влияние возмущения на регулируемую величину оказывается существенно уменьшенным, но проявляет себя в переходных и установившихся режимах. В том случае достигают инвариантности с точностью до малой величины e.

Аналогично классифицируют инвариантность рассогласования от задающего воздействия в комбинированных следящих системах (рисунок 1.2).

Анализ инвариантности САУ составляет одну из типовых задач теории инвариантности. В случае простейшей системы управления по возмущению (рисунок 2.47) названную задачу решать проще в рамках классической ММ типа «вход — выход» (см. п. 2.1.1.3). При этом операторное уравнение

связывает изображение ошибки регулирования E(s) с изображением по Лапласу возмущения Z(s). В области оригиналов решением этого уравнения является функция времени

где eп(t) и eв(t) – соответственно переходная и вынужденная составляю­щие ошибки e(t).

На рисунке 2.48 изображена структурная схема исследуемой системы. Изображение ошибки E(s) при нулевых НУ представляют в виде дробно-рациональной функции

или .

Поскольку изображение возмуще­ния Z(s) в общем случае представляет собой дробно-рациональную функцию вида

,

то изображение ошибки

. (2.110)

Изображению ошибки E(s) соответствует оригинал e(t), который на основании теоремы разложения (см. п. 2.1.7.3) может быть при отсутствии кратных корней представлен в следующем виде:

, (2.111)

где sk – полюсы изображения ошибки E(s), т.е. корни уравнения A(s) = 0;

si – полюсы изображения возмущения Z(s), т.е. корни уравнения C(s) = 0.

Согласно определению, САУ инвариантна от возмущения z(t), если вынужденная составляющая ошибки тождественно равна нулю eв(t) º 0. В соответствии с (2.110) это возможно в трех случаях.

В первом случае eв(t) º 0, если D(s) = 0. Этот случай считают тривиальным, так как он отличается отсутствием возмущения и практичес­кого интереса не представляет.

Во втором случае eв(t) º 0, если B(s) = 0. Условие B(s) = 0 означает равенство нулю ПФ по возмущающему воздействию Wz(s) = 0. Принципиально это случай абсолютной инвариантности САУ от возмущения z(t), которое может быть любой функцией времени. Однако реализация условия B(s) = 0 встречает значительные технические трудности.

В третьем случае равенства eв(t) º 0 можно достичь только для тех функций z(t), изображения которых Z(s) имеют все полюсы si, совпадающие с нулями E(s), т.е. с корнями уравнения B(s) = 0. В этом случае после разложения на множители полиномов B(s) и C(s) сокращаются одинаковые сомножители вида (s — si) в числителе и знаменателе выражения (2.110). В итоге второе слагаемое в выражении (2.111) обращается в нуль и eв(t) º 0. Рассмотренный случай соответствует частичной инвариантности.

Таким образом, для инвариантности ошибки регулирования e(t) или регулируемой величины y(t) от возмущающего воздействия z(t) ПФ САУ относительно этого возмущения Wz(s), составленная для e(t) или y(t), должна быть тождественно равна нулю

Тождество (2.112) удовлетворяется тогда, и только тогда, когда B(s) = 0, или

Реализация условия инвариантности Wz(s) = 0 достигается синтезом УУ (компенсатора). Непосредственно ПФ компенсатора Wуу(s) получают по условию инвариантности. Очевидно, что ПФ системы по возмущению является эквивалентной и согласно (2.27) и (2.28) Wz(s) = Wze(s) + Wуу(s)Wоу(s). Поскольку Wz(s) = 0, то УУ должно иметь ПФ:

.

Полученные результаты в равной степени справедливы и для комбинированной САУ (рисунок 1.4), инвариантной от управляющего (задающего) воздействия g(t).

2.4.3 Анализ чувствительности САУ

Параметры САУ зависят от физических параметров ее элементов (сопротивления, индуктивности, емкости, массы, момента инерции и т.д.). В процессе работы системы эти физические параметры могут по разным причинам изменяться во времени.

Поэтому возникает задача определения влияния изменения параметров САУ на статические и динамические характеристики процесса управления, т.е. на точность САУ и ее временнÏе и частотные характеристики.

Свойство САУ изменять свои выходные характеристики (показатели качества регулирования) при отклонении тех или иных параметров от своих (расчетных) значений называют чувствительностью системы. Названное отклонение параметров системы обусловливает отличие варьированного движения от исходного движения САУ y1(t), y2(t), …, yn(t). Эту разницу

, i = 1, 2, …, n

называют дополнительным движением системы и рассчитывают по формуле

(2.113)

где uij – функции чувствительности (j = 1, 2, …, m);

aj – параметры САУ, изменяющиеся со временем.

Различают функции чувствительности:

– передаточных функций

– временнÏх характеристик ;

– показателей (критериев) качества .

Определение функций чувствительности проводят следующим образом. САУ описывают системой ОДУ в нормальной форме Коши

, (2.114)

где yi – переменные состояния, i = 1, 2, …, n (см. систему уравнений (2.68)).

Изменяющиеся со временем параметры входят в коэффициенты уравнений (2.114), т.е. , , …, .

Уравнения САУ (2.114) преобразуют к следующему виду:

Дифференцируя последние уравнения, получают уравнения чувствительности

. (2.115)

Функции чувствительности uijполучают решением названных уравнений. Определение функций чувствительности простейших САУ не вызывает серьезных затруднений. В частности, такая система подобна А‑звену первого порядка и описывается ОДУ (таблица 2.1)

.

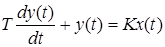
В этом случае временнÏе характеристики САУ чувствительны к изменениям коэффициента передачи K и постоянной времени T. Для количественной оценки этой зависимости вводят соответственно две функции чувствительности

и .

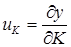
Для определения этих функций ОДУ системы приводят к нормальной форме Коши (2.113):

или в общем виде при i = 1

,

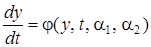
где .

Изменяющиеся параметры обозначены a1= T и a2= K.

Согласно (2.114) при i = 1 и j = 2

Окончательно получают уравнения чувствительности

Интегрирование уравнений чувствительности приводит к искомым функциям чувствительности uTи uKи оценке дополнительного движения САУ DyTи DyK.

Задачу определения функций чувствительности uijи дополнительного движения DyiСАУ с постоянными параметрами решают также с помощью преобразования Лапласа. Для этого основную ПФ системы, у которой параметры имеют отклонение на величину a от номинального значения, обозначают F(s, a). В этом случае оригинал регулируемой (выходной) величины определяют обратным преобразованием Лапласа

,

где X(s) – изображение входного сигнала системы x(t).

Если это уравнение дифференцируемо по параметру a, то функция чувствительности равна

.

В рассмотренном выше примере анализа чувствительности А-звена первого порядка к изменению постоянной времени T при x(t) = 1(t) следует принять соответственно

и .

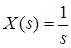
При этом функция чувствительности равна

Дополнительное движение определяется согласно (2.113) и равно

Регулируемая величина звена с постоянной времени T + a изменяется по следующему закону

На рисунке 2.49 показаны графики функций и , изображающие соответственно варьированное и исход­ное движение исследуемого А‑звена.

2.4.4 Анализ управляемости и наблюдаемости линейных САУ

Для анализа управляемости и наблюдаемости САУ необходимо ММ системы привести к виду «вход – состояние – выход» (рисунок 2.27), так как исследуемые свойства системы непосредственно связаны со структу­рой матриц A, B и C уравнений состояния (2.82).

Понятие управляемости связано с возможностью приведения системы в заданное состояние с помощью управляющих (входных) воздействий.

Понятие наблюдаемости САУ связано с возможностью определения переменных состояния по результатам измерения выходных переменных.

На рисунке 2.50 в качестве примера изображена структурная схема некоторой САУ.

Переменная состояния не связа­на с входным воздействием u(t), которое поэтому не влияет на изменение во времени. Такую переменную состояния называют неуправляемой. Переменная не связана с выходом, и поэтому по наблюдению выхода y(t) невозможно определить . Такую переменную состояния называют ненаблюдаемой.

Р.Калманом предложено следующее определение: САУ (2.82) называют полностью управляемой, если для любых моментов времени t0 и t1(t1 > t0) и любых заданных состояний X0и X1существует управление u(t) (t0 £ t £ t1), переводящее начальное состояние X(t0) = X0в конечное X(t1) = X1.

Для оценки управляемости САУ вводят в рассмотрение матрицу управляемости

которая состоит из столбцов матриц B и произведений матриц AB, A2B и т.д. и имеет размерность [n ´ nm]. Первая теорема Калмана устанавливает условие (критерий) управляемости: САУ (2.82) полностью управляема тогда и только тогда, когда ранг матрицы управляемости У равен n, т.е.

Если ранг матрицы управляемости rankУ 2 Cт … Aт n -1 Cт], (2.118)

которая состоит из столбцов матриц Cт, произведений матриц AтCт, Ат 2 Cт … Aт n — 1 Cти имеет размерность [n ´ pn].

Вторая теорема Калмана устанавливает условие (критерий) наблюдаемости: САУ (2.82) вполне наблюдаема (восстанавливаема) тогда и только тогда, когда ранг матрицы наблюдаемости Н равен n, т.е.

Если rankН A(w). На правой границе полосы A(wп) = 0,707A(0). В полосе пропускания сигналы всех частот проходят практически без ослабления. Полоса пропускания не должна быть слишком широкой. В противном случае САУ будет воспроизводить высокочастотные помехи.

2.4.5.3 Корневые критерии

Корневыми называют критерии, основанные на расположении корней характеристического уравнения замкнутой САУ (2.8), т.е. полюсов piосновной ПФ F(s), а также и нулей zjэтой ПФ.

В этом случае основную ПФ системы записывают в следующем виде:

,

где zj – нули ПФ, зависящие от места приложения воздействия;

Очевидно, что полюсы и нули определяют основную ПФ системы F(s). Следовательно, изучая их расположение на комплексной плоскости, можно судить о качестве переходных процессов в САУ.

Если ПФ не имеет нулей, т.е.

,

то качество переходных процессов в САУ оценивают по корням ее характеристического уравнения pi.

Согласно (2.107) переходный процесс в устойчивой САУ слагается из затухающих апериодических и колебательных составляющих. Первые определяются действительными корнями характеристического уравнения, а вторые – парами сопряженных комплексных корней. При этом необходимо найти длительность tрсамой продолжительной составляющей и колебательность K (или n) самой колебательной составляющей, которые позволяют оценить верхние пределы длительности tри колебательности K всего переходного процесса в САУ.

Быстродействие САУ определяют по степени устойчивости h, т.е. по расстоянию h от мнимой оси комплексной плоскости до ближайшего к ней вещественного корня (рисунок 2.55) или пары комплексно-сопряженных корней (рисунок 2.3).

Если корень вещественный, то степень устойчивости называют апериодической. В этом случае в переходном процессе доминирует экспоненциальная тенденция, характеризуемая этим корнем. Названная экспонента определяет время регулирования (D = 5 %):

. (2.128)

Если ближайшими к мнимой оси является пара комплексно-сопряженных корней, степень устойчивости h называют колебательной. При колебательной степени устойчивости переходная характеристика изображается затухающей синусоидой (рисунки 2.51 и 2.52), огибающая которой описывается уравнением экспоненты вида (2.107). Поэтому время регулирования tртакже можно рассчитать по (2.127). Таким образом, степень устойчивости h служит критерием длительности процесса регулирования tр(быстродействия САР).

Критерием колебательности САУ служит степень колебательности m:

, (2.129)

где a и b – соответственно действительная и мнимая части корней pi, i+1 = a ± b характеристического уравнения САР D(s) = 0.

Степень колебательности m характеризует быстроту затухания амплитуды колебаний регулируемой величины y(t) за каждый период t = 2p/bi(рисунок 2.51) и, следовательно связана с колебательностью соотношением

. (2.130)

Чем больше m, тем больше колебательность переходного процесса K. Наиболее колебательной является составляющая , у которой отношение bi/aiмаксимально (см. (2.129)). Таким образом, степень колебательности m является оценкой сверху колебательности K. Иногда при синтезе САР в расчетах используют обратную степени колебательности m величину

. (2.131)

2.4.5.4 Интегральные критерии

Интегральными критериями называют такие, которые одним числом оценивают величины отклонений и время затухания переходного процесса.

Интегральные оценки удобны для сравнения близких по свойствам САР (лучшая из них имеет меньшую интегральную оценку) и для выбора параметров САР при синтезе (см. п. 3).

Интегральные оценки являются функционалами и записываются в виде интегралов

где f(t) – функция, характеризующая процесс регулирования;

F – заданная функция.

Минимальное значение данного функционала обеспечивает оптимальный процесс регулирования (управления).

Практическое распространение получили линейные и квадратичные интегральные оценки.