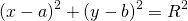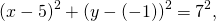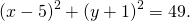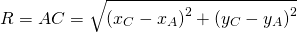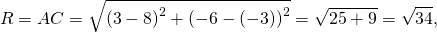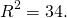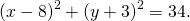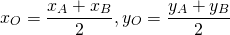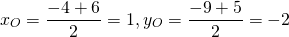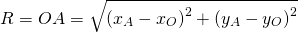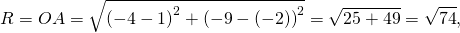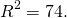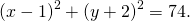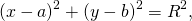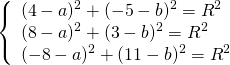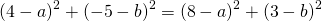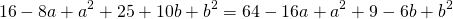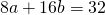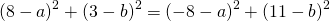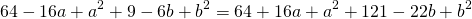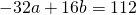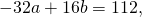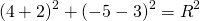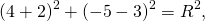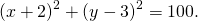Как записать уравнение круга которое в круг

Уравнение окружности.

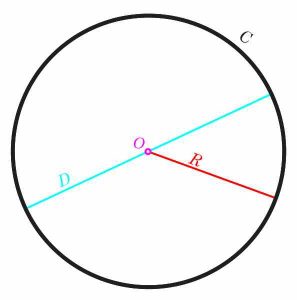
Окружностью принято обозначать множество всех точек плоскости, равноудаленных от одной точки – от центра.

В формулировке окружности упоминается расстояние между точкой окружности и центром.

Формула расстояния между двумя точками М₁(х₁; у₁) и М₂(х₂; у₂) имеет вид:

,

Применив формулу и формулировку окружности, получаем уравнение окружности с центром в точке С (х₀; у₀) и радиусом r.

Отметим произвольную точку М(х; у) на этой окружности.

.

Предположим, что М принадлежит окружности с центром С и радиусом r, то МС = r.

Следовательно, МС 2 = r 2 и координаты точки М удовлетворяют уравнению окружности (х – х₀ ) 2 +(у – у₀ ) 2 = r 2 .

Из выше изложенного делаем вывод, что уравнение окружности с центром в точке С (х₀; у₀) и радиусом r имеет вид:

В случае когда центр окружности совпадает с началом координат, то получаем частный случай уравнения окружности с центром в точке О (0;0):

Уравнение круга

Круг — одна из самых заметных геометрических фигур. Он обладает замечательной симметрией, основанной на том факте, что ВСЕ точки в круге равноудалены от центра, что на английском языке означает, что все точки в круге находятся на одинаковом расстоянии от центра. Это общее расстояние \(r\) называется радиус круга .

У круга есть много важных геометрических приложений, которые делают его действительно важным объектом как в геометрии, так и в алгебре.

Еще одно важное свойство круга — это то, что его очень легко представить алгебраически. Это означает, что мы можем легко задать уравнение для представления всех точек данного круга. Говоря более конкретно, рассмотрим координатную плоскость \(X — Y\). Все это означает, что у нас есть оси X и Y, которые перпендикулярны друг другу.

Уравнение круга

Теперь давайте поговорим об уравнении, которое представляет все точки данного круга. Действительно, для окружности радиуса \(r\) следующее уравнение описывает точки \((x, y)\), которые находятся на окружности:

\[\Large x^2 + y^2 = r^2\]

Вышеупомянутое соответствует уравнению круга радиуса \(r\) с центром, расположенным в \((0,0)\), начале координат осей.

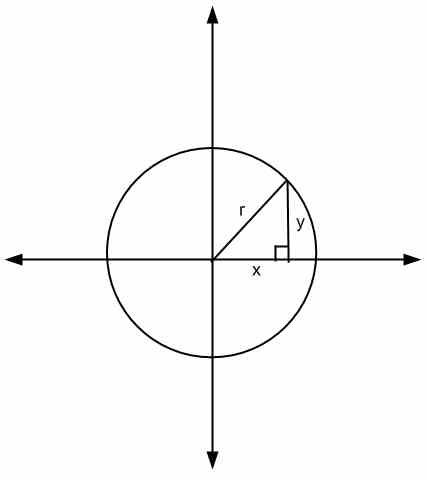
Если смотреть на уравнение выше, геометрическая интерпретация состоит в том, что \(x\) и \(y\) — это стороны треугольника, а \(r\) — его гипотенуза.

Другой способ увидеть уравнение круга — извлечь квадратный корень из обеих сторон уравнения, так что мы получим \(\sqrt = r\), что указывает на то, что для любой точки \((x,y)\) на круге расстояние до начала координат (в данном случае центр круга) равно \(r\).

Уравнение круга, не центрированного в начале координат

Одним из преимуществ работы по скоординированным осям является то, что точки на окружности и в центре могут быть локализованный по осям, и может быть представлено уравнением, как показано выше. Но в целом центр круга не обязательно должен быть началом координат, это может быть любая точка \((x_0, y_0\) на согласованных осях, и в этом случае уравнение круга становится:

\[\Large (x-x_0)^2 + (y-y_0)^2 = r^2\]

который известен как Общее уравнение круга . Например, скажем, вам нужно вычислить уравнение круга радиуса \(r = 4\), который центрирован в точке \((1,2)\). Итак, в этом случае у нас есть \(x_0 = 1\), \(y_0 = 2\) и \(r = 4\), а затем мы просто вставляем эти числа в приведенное выше уравнение и получаем

\[\large (x-1)^2 + (y-2)^2 = 4^2\]

или мы также можем написать

\[\large (x-1)^2 + (y-2)^2 = 16\]

ПРИМЕР 1

Напишите уравнение окружности радиуса 3 с центром в начале координат. Используя уравнение, определите, принадлежит ли точка (1, 2) окружности.

ОТВЕЧАТЬ:

Для начала определим уравнение круга. В этом случае круг центрируется в начале координат, поэтому \((x_0, y_0) = (0, 0)\). Следовательно, уравнение имеет вид

\[\large x^2 + y^2 = 3^2\]

который совпадает с

\[\large x^2 + y^2 = 9\]

Теперь вопрос в том, находится ли точка (1, 2) на окружности. Мы знаем, что точки на круге будут такими, что \(x^2 + y^2 = 9\). Для точки \((1, 2)\) мы получаем \(x = 1\) и \(y=2\), поэтому в этом случае для этой точки \(x^2 + y^2 = 1^2 + 2^2 = 1+ 4 = 5\), который отличается от 9, и, следовательно, \((1,2)\) не принадлежит кругу.

Подробнее об уравнении круга

Круг — настолько важный математический объект, что о нем написаны тома книг. Круги пересекают геометрию, тригонометрию и алгебру, поэтому в математике они встречаются как поперечные.

Как составить уравнение круга?

Когда мы работаем с кругом, нужно работать над несколькими вещами. Первым делом нужно построить уравнение круга. Например, рассмотрим круг радиуса \(r = 3\) с центром в точке \((1,1)\). Основываясь на общем уравнении круга, уравнение имеет вид

\[\large (x-1)^2 + (y-1)^2 = 3^2\]

Приведенное выше уравнение можно использовать, например, для определения того, принадлежит ли точка окружности или нет. Что еще можно сделать, чтобы составить уравнение круга? Вы можете потенциально расширить квадраты, поэтому мы получаем

\[\large x^2 — 2x + 1 + y^2 -2y + 1 = 9\]

который можно упростить до

\[\large x^2 — 2x + y^2 -2y = 7\]

Итак, оба уравнения эквивалентны в том смысле, что они определяют один и тот же круг. Какой из них вы предпочитаете? \((x-1)^2 + (y-1)^2 = 3^2\) или \(x^2 — 2x + y^2 -2y = 7\)? Это вопрос вкуса и того, для чего вы будете использовать формулу.

Является ли уравнение круга функцией?

Это вопрос, который задают многие студенты, и нам необходимо его прояснить. Прежде всего, уравнение круга — это уравнение, а не отношение или функция. Теперь уравнение круга определяет отношение, а не функцию, когда вы алгебраически решаете для \(y\) в терминах \(x\). Действительно, если мы решим \(y\), мы получим:

\[\large x^2 + y^2 = 9 \Rightarrow y^2 = 9 — x^2 \] \[\large \Rightarrow y = \pm \sqrt < 9 - x^2>\]

Это означает, что для данного \(x\) есть два связанных значения \(y\): \(\sqrt< 9 - x^2>\) и \(-\sqrt< 9 - x^2>\), что указывает на то, что уравнение круга определяет отношение, а не функцию.

Частным случаем круга является единичный круг с уравнением \(x^2 + y^2 = 1\), которое центрируется в начале координат. Единичный круг особенно подходит для визуальной работы с тригонометрическими выражениями.

Написать уравнение окружности

Рассмотрим некоторые примеры, в которых требуется написать уравнение окружности по заданным условиям.

1) Написать уравнение окружности с центром в точке K(5;-1) и радиусом 7.

Уравнение окружности с центром в точке (a;b) и радиусом R имеет вид:

Так как центр окружности — точка K(5; -1), то a=5, b=-1.Подставляем эти данные в уравнение окружности:

2) Напишите уравнение окружности с центром в точке A (8;-3) проходящей через точку C(3;-6).

Так как центр окружности — точка A(8; -3), то a=8, b=-3.

Остаётся найти радиус. Он равен расстоянию от центра окружности до точки, лежащей на окружности, то есть в данном случае радиус окружности равен расстоянию между точками A и C.

Следовательно, уравнение данной окружности

3) Составить уравнение окружности, диаметром которой является отрезок AB, если A (-4; -9), B(6;5).

Центром окружности является середина диаметра, в нашем случае — середина отрезка AB. По формулам координат середины отрезка

Центр окружности — точка O(1;-2). Значит, a=1, b=-2.

Радиус можно найти как расстояние от центра окружности до любой из точек A или B окружности. Например,

Таким образом, уравнение окружности с диаметром AB —

4) Написать уравнение окружности, проходящей через три точки: A(4; -5), B(8; 3) C(-8; 11).

Так как точки A, B C принадлежат окружности, то их координаты удовлетворяют уравнению окружности. Подставив координаты точек в уравнение

получаем систему уравнений:

Поскольку правые части уравнений равны, левые также равны. Приравняв правые части 1-го и 2-го уравнений получим

Приравняем правые части 2-го и 3-го уравнений:

на -1 и сложив результат почленно с уравнением

получаем a=-2, b=3. Подставив этот результат в первое уравнение системы:

Следовательно, уравнение окружности, проходящей через три данные точки —

5) Написать уравнение окружности, описанной около треугольника ABC с вершинами в точках A(2; 6), B(1; 5) C(8; -2).

Решение аналогично решению задания 4. В результате получим уравнение