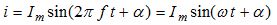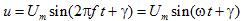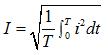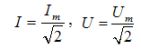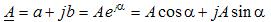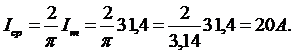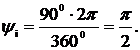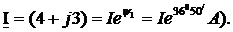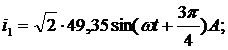Как записать уравнение мгновенного значения напряжения

Переменный электрический ток

Переменный ток (AC — Alternating Current) — электрический ток, меняющий свою величину и направление с течением времени.

Часто в технической литературе переменным называют ток, который меняет только величину, но не меняет направление, например, пульсирующий ток.
Необходимо помнить при расчётах, что переменный ток в этом случае является лишь составляющей частью общего тока.
Такой вариант можно представить как переменный ток AC с постоянной составляющей DC. Либо как постоянный ток с переменной составляющей, в зависимости от того, какая составляющая наиболее важна в контексте.

DC — Direct Current — постоянный ток, не меняющий своей величины и направления.

В реальности постоянный ток не может сохранять свою величину постоянной, поэтому существует условно в тех случаях, где можно пренебречь изменениями его постоянной величины, либо в качестве составляющей (DC) для периодически меняющегося электрического тока любой формы. Тогда величина DC будет равна среднему значению тока за период, и будет являться нулевой линией для переменной составляющей AC.

При синусоидальной форме тока, например в электросети, постоянная составляющая DC равна нулю.

Постоянный ток с переменной составляющей в виде пульсаций показан синей линией на верхнем графике рисунка.
Запись AC+DC в данном случае не является математической суммой, а лишь указывает на две составляющие тока. Суммируются мощности.
Величина тока будет равна квадратному корню из суммы квадратов двух величин — значения постоянной составляющей DC и среднеквадратичного значения переменной составляющей AC.

Термины AC и DC применимы как для тока, так и для напряжения.

Параметры переменного тока и напряжения

Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:

Период T — время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.

Частота f — величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz). Частота f = 1 /T

Циклическая частота ω — угловая частота, равная количеству периодов за 2π секунд.

Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°

Начальная фаза ψ — величина угла от нуля (ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.

Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.

Мгновенное значение — величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t.

Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:

i = I ampsin(ωt); u = U ampsin(ωt)

С учётом начальной фазы:

i = I ampsin(ωt + ψ); u = U ampsin(ωt + ψ)

Здесь I amp и U amp — амплитудные значения тока и напряжения.

Амплитудное значение — максимальное по модулю мгновенное значение за период.

Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) — максимальное отклонение от нулевого значения.

Среднее значение (avg) — определяется как среднеарифметическое всех мгновенных значений за период T.

Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.

Средневыпрямленное значение — среднеарифметическое модулей всех мгновенных значений за период.

Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.

Среднеквадратичное значение (rms) — определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.

Для синусоидального тока и напряжения амплитудой I amp (U amp) среднеквадратичное значение определится из расчёта:

Среднеквадратичное — это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.

Коэффициент амплитуды и коэффициент формы

Для удобства расчётов, связанных с измерением действующих значений при искажённых формах тока, используются коэффициенты, которыми связаны между собой амплитудное, среднеквадратичное и средневыпрямленное значения.

Коэффициент амплитуды — отношение амплитудного значения к среднеквадратичному.
Для синусоидального тока и напряжения коэффициент амплитуды K_A = √2 ≈ 1.414
Для тока и напряжения треугольной или пилообразной формы коэффициент амплитуды K_A = √3 ≈ 1.732
Для переменного тока и напряжения прямоугольной формы коэффициент амплитуды K_A = 1

Коэффициент формы — отношение среднеквадратичного значения к средневыпрямленному.
Для переменного синусоидального тока или напряжения коэффициент формы K_Ф ≈ 1.111
Для тока и напряжения треугольной или пилообразной формы K_Ф ≈ 1.155
Для переменного тока и напряжения прямоугольной формы K_Ф = 1

Замечания и предложения принимаются и приветствуются!

Аналитические выражения для тока и напряжения

Любой ток изменяющийся по величине является переменным. Но на практике под переменным током понимают такой ток, закон изменения которого во времени есть синусоидальная функция.

Математическое выражение для синусоидального тока можно записать в виде:

где, i – мгновенное значение тока, показывающее величину тока в конкретный момент времени, Im – амплитудное (максимальное) значение тока, выражение в скобках есть фаза, которая определяет значение тока в момент времени t, f – частота переменного тока, это величина, обратная периоду изменения синусоидальной величины Т, ω – угловая частота, ω = 2πf = 2π / T , α – начальная фаза, показывает значение фазы в момент времени t = 0.

Аналогичное выражение можно записать и для синусоидального переменного напряжения:

Мгновенные значения тока и напряжения условились обозначать строчными латинскими буквами i, u, а максимальные (амплитудные) значения – прописными печатными латинскими буквами I, U с индексом m.

Для измерения величины переменного тока чаще всего используют действующее (эффективное) значение , которое численно равно такому постоянному току, который за период переменного выделяет в нагрузке такое же количество тепла, что и переменный ток.

Действующее значение переменного тока :

Для обозначения действующих значений тока и напряжения используют прописные печатные латинские буквы I, U без индекса.

В цепях синусоидального тока между амплитудным и действующим значениями существует взаимосвязь:

В цепях переменного тока изменение во времени питающего напряжения влечёт за собой изменение тока, а также магнитного и электрического полей, связанных с цепью. Результатом этих изменений является возникновение ЭДС самоиндукции и взаимоиндукции в цепях с катушками индуктивности, а в цепях с конденсаторами появляются зарядные и разрядные токи, которые создают сдвиг по фазе между напряжениями и токами в таких цепях.

Отмеченные физические процессы учитывают введением реактивных сопротивлений , в которых, в отличие от активных, не происходит превращение электрической энергии в другие виды энергии. Наличие тока в реактивном элементе объясняется периодическим обменом энергией между таким элементом и сетью. Все это усложняет расчёт цепей переменного тока, так как приходится определять не только величину тока, но и его угол сдвига по отношению к напряжению.

Все основные законы цепей постоянного тока справедливы и для цепей переменного тока, но только для мгновенных значений или значений в векторной (комплексной) форме. На основе этих законов можно составить уравнения, позволяющие осуществить расчёт цепи.

Как правило, целью расчёта цепи переменного тока является определение токов, напряжений, углов сдвига фаз и мощностей на отдельных участках . При составлении уравнений для расчёта таких цепей выбирают условные положительные направления ЭДС, напряжений и токов. Получаемые уравнения для мгновенных значений в установившемся режиме и синусоидальном входном напряжении будут содержать синусоидальные функции времени.

Аналитический расчёт тригонометрических уравнений неудобен, требует значительных затрат времени и поэтому не находит широкого распространения в электротехнике. Упростить анализ цепи переменного тока можно, используя тот факт, что синусоидальную функцию можно условно изобразить вектором, а вектор, в свою очередь, можно записать в виде комплексного числа .

Комплексным числом называют выражение вида:

где a – вещественная (действительная) часть комплексного числа, j – мнимая единица, b – мнимая часть, A – модуль, α – аргумент, e – основание натурального логарифма.

Первое выражение представляет собой алгебраическую форму записи комплексного числа, второе – показательную, а третье – тригонометрическую. Для отличия, в комплексной форме записи подчеркивают букву, обозначающую электрический параметр.

Метод расчёта цепи, основанный на применении комплексных чисел, называется символическим методом . В символическом методе расчета все реальные параметры электрической цепи заменяют символами в комплексной форме записи. После замены реальных параметров цепи на их комплексные символы расчет цепей переменного тока выполняют методами, которые применяли для расчета цепей постоянного тока. Отличие состоит в том, что все математические операции необходимо выполнять с комплексными числами.

В результате расчета электрической цепи искомые токи и напряжения получаются в виде комплексных чисел. Реальные действующие значения тока или напряжения равны модулю соответствующего комплекса, а аргумент комплексного числа показывает угол поворота вектора на комплексной плоскости по отношению к положительному направлению вещественной оси. При положительном аргументе вектор поворачивается против часовой стрелки, а в случае отрицательного аргумента – по часовой.

Завершают расчёт цепи переменного тока, как правило, составлением баланса активных и реактивных мощностей, который позволяет проверить правильность вычислений.

Любой ток изменяющийся по величине является переменным. Но на практике под переменным током понимают такой ток, закон изменения которого во времени есть синусоидальная функция.

Математическое выражение для синусоидального тока можно записать в виде:

где, i – мгновенное значение тока, показывающее величину тока в конкретный момент времени, Im – амплитудное (максимальное) значение тока, выражение в скобках есть фаза, которая определяет значение тока в момент времени t, f – частота переменного тока, это величина, обратная периоду изменения синусоидальной величины Т, ω – угловая частота, ω = 2πf = 2π / T , α – начальная фаза, показывает значение фазы в момент времени t = 0.

Аналогичное выражение можно записать и для синусоидального переменного напряжения:

Мгновенные значения тока и напряжения условились обозначать строчными латинскими буквами i, u, а максимальные (амплитудные) значения – прописными печатными латинскими буквами I, U с индексом m.

Для измерения величины переменного тока чаще всего используют действующее (эффективное) значение , которое численно равно такому постоянному току, который за период переменного выделяет в нагрузке такое же количество тепла, что и переменный ток.

Действующее значение переменного тока :

Для обозначения действующих значений тока и напряжения используют прописные печатные латинские буквы I, U без индекса.

В цепях синусоидального тока между амплитудным и действующим значениями существует взаимосвязь:

В цепях переменного тока изменение во времени питающего напряжения влечёт за собой изменение тока, а также магнитного и электрического полей, связанных с цепью. Результатом этих изменений является возникновение ЭДС самоиндукции и взаимоиндукции в цепях с катушками индуктивности, а в цепях с конденсаторами появляются зарядные и разрядные токи, которые создают сдвиг по фазе между напряжениями и токами в таких цепях.

Отмеченные физические процессы учитывают введением реактивных сопротивлений , в которых, в отличие от активных, не происходит превращение электрической энергии в другие виды энергии. Наличие тока в реактивном элементе объясняется периодическим обменом энергией между таким элементом и сетью. Все это усложняет расчёт цепей переменного тока, так как приходится определять не только величину тока, но и его угол сдвига по отношению к напряжению.

Все основные законы цепей постоянного тока справедливы и для цепей переменного тока, но только для мгновенных значений или значений в векторной (комплексной) форме. На основе этих законов можно составить уравнения, позволяющие осуществить расчёт цепи.

Как правило, целью расчёта цепи переменного тока является определение токов, напряжений, углов сдвига фаз и мощностей на отдельных участках . При составлении уравнений для расчёта таких цепей выбирают условные положительные направления ЭДС, напряжений и токов. Получаемые уравнения для мгновенных значений в установившемся режиме и синусоидальном входном напряжении будут содержать синусоидальные функции времени.

Аналитический расчёт тригонометрических уравнений неудобен, требует значительных затрат времени и поэтому не находит широкого распространения в электротехнике. Упростить анализ цепи переменного тока можно, используя тот факт, что синусоидальную функцию можно условно изобразить вектором, а вектор, в свою очередь, можно записать в виде комплексного числа .

Комплексным числом называют выражение вида:

где a – вещественная (действительная) часть комплексного числа, j – мнимая единица, b – мнимая часть, A – модуль, α – аргумент, e – основание натурального логарифма.

Первое выражение представляет собой алгебраическую форму записи комплексного числа, второе – показательную, а третье – тригонометрическую. Для отличия, в комплексной форме записи подчеркивают букву, обозначающую электрический параметр.

Метод расчёта цепи, основанный на применении комплексных чисел, называется символическим методом . В символическом методе расчета все реальные параметры электрической цепи заменяют символами в комплексной форме записи. После замены реальных параметров цепи на их комплексные символы расчет цепей переменного тока выполняют методами, которые применяли для расчета цепей постоянного тока. Отличие состоит в том, что все математические операции необходимо выполнять с комплексными числами.

В результате расчета электрической цепи искомые токи и напряжения получаются в виде комплексных чисел. Реальные действующие значения тока или напряжения равны модулю соответствующего комплекса, а аргумент комплексного числа показывает угол поворота вектора на комплексной плоскости по отношению к положительному направлению вещественной оси. При положительном аргументе вектор поворачивается против часовой стрелки, а в случае отрицательного аргумента – по часовой.

Завершают расчёт цепи переменного тока, как правило, составлением баланса активных и реактивных мощностей, который позволяет проверить правильность вычислений.

Мгновенные значения синусоидальной функции времени	Формы представления комплексных чисел
Показательная	тригонометрическая	алгебраическая

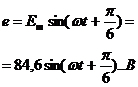В таблице 1 показан переход от записи мгновенных значений синусоидальных функций времени к показательной, тригонометрической и алгебраической формам записи комплексных чисел(максимальное значение ЭДС E_m = 84,6 В, действующее ее значение 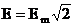= 60 В).

Практическая часть

Задание 1.

Определить среднее значение синусоидального тока I_ср по мгновенному его значению i =31,4 sin(ωt + π/2).Записать мгновенный ток в тригонометрической, показательной и алгебраической формах.

Решение.

ВАРИАНТЫ

Задание 2

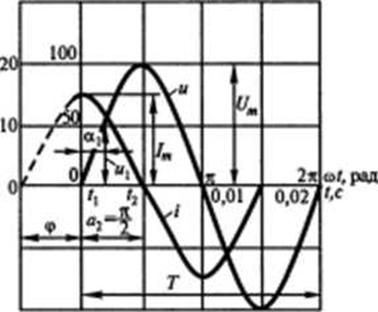
Для синусоидального напряжения и тока (рисунок 3) записать выражения для мгновенных их значений. Определить период Т и время t , соответствующее начальной фазе тока а также мгновенные значения напряжений u₁ и u₂ для моментов времени t_{1 =} 0,00167 с и t₂ = 0,005 с, если частота тока f = 50 Гц.

Решение.

u = U_m sin ωt = 100 sin 314 t В,

Задание 3

В условиях задания 2 записать выражения для мгновенных значений напряжения и, соответствующих моментам времени t₁, и t₂.

Решение:

Задание 4

Представить комплексный ток А в тригонометрической и показательной и мгновенной формах записи.

Решение.

А.

ВАРИАНТЫ

Вариант	Комплексный ток	Ответ

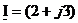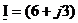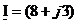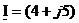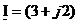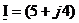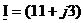Задание 5

Записать выражение для комплексной амплитуды тока I_m исходя из выражения для мгновенного его значения i = 10 sin (ωt + 30°) А.

Решение.

ВАРИАНТЫ

Задание 6

Представить комплексный ток . в алгебраической (координатной) форме записи.

Решение.

Вариант	Комплексный ток	Ответ

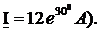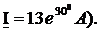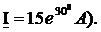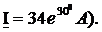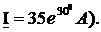Задание 7

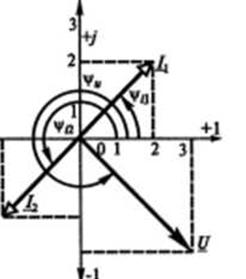
На комплексной плоскости (рисунок 4) приведена векторная диаграмма токов и напряжений. Представить токи I₁, и I₂, и напряжение U в алгебраической форме записи и найти их аргументы.

Решение.

; ; В.

: tgᴪ_i1 = 2/2 = 1.

= = 225°

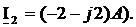
Задание 8.

На плоскости комплексных чисел (рисунок 5) заданы комплексные напряжение и токи и электрической цепи. Представить их в алгебраической и показательной формах записи.

= (25 + j725) В; = (-35 + j35) А; = -45 A.

Задание 9

В условиях задания 8 записать аналитические выражения для мгновенных значений напряжения u и токов i₁, и i₂, считая, что положения векторов токов 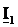, и и напряжения на плоскости комплексных чисел даны для момента времени t = 0.

Контрольные вопросы

1. Что такое амплитудно-частотная характеристика?

2. Что такое фазовая частотная характеристика?

3. Как по АЧХ определить полосу пропускания?

4. Как экспериментально определить резонасную частоту при параллельном соединении R,L,C?

5. Приведите примеры использования резонансных явлений.

6. Дайте определение характеристического сопротивления резонансного контура.

7. Какой характер имеет сопротивление контура при w > w ?

8. От чего зависит добротность резонансного контура?

9. Нарисуйте векторную диаграмму в параллельном колебательном контуре.

10. Как вычислить резонансную частоту при резонансе напряжений?

11. Как по схеме двухполюсника без потерь определить характер частотных характеристик.

12. Как построить частотные характеристики параллельного резонансного контура по схеме?

Как записать уравнение мгновенного значения напряжения

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, — периодом Т. Для периодического тока имеем

,

(1)

Величина, обратная периоду, есть частота, измеряемая в герцах (Гц):

,

(2)

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01 ¸ 10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i — мгновенное значение тока ;

u – мгновенное значение напряжения ;

е — мгновенное значение ЭДС ;

р — мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ) .

— амплитуда тока;

— амплитуда напряжения;

— амплитуда ЭДС.

Действующее значение переменного тока

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

,

(3)

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных ЭДС, напряжений
и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂ соответствуют уравнения:

.

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени ( t =0): и — начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

.

Векторное изображение синусоидально
изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂ (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени ( t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

.

Каждый из этих токов синусоидален и может быть представлен уравнением

и .

Результирующий ток также будет синусоидален:

.

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы.

На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов для t =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Представление синусоидальных ЭДС, напряжений
и токов комплексными числами

Геометрические операции с векторами можно заменить алгебраическими операциями с комплексными числами, что существенно повышает точность получаемых результатов.

Каждому вектору на комплексной плоскости соответствует определенное комплексное число, которое может быть записано в :

показательной

тригонометрической или

алгебраической — формах.

Например, ЭДС , изображенной на рис. 7 вращающимся вектором, соответствует комплексное число

.

Фазовый угол определяется по проекциям вектора на оси “+1” и “+j” системы координат, как

.

В соответствии с тригонометрической формой записи мнимая составляющая комплексного числа определяет мгновенное значение синусоидально изменяющейся ЭДС:

,

(4)

Комплексное число удобно представить в виде произведения двух комплексных чисел:

,

(5)

Параметр , соответствующий положению вектора для t =0 (или на вращающейся со скоростью w комплексной плоскости), называют комплексной амплитудой: , а параметр — комплексом мгновенного значения.

Параметр является оператором поворота вектора на угол w t относительно начального положения вектора.

Вообще говоря, умножение вектора на оператор поворота есть его поворот относительно первоначального положения на угол ± a .

Следовательно, мгновенное значение синусоидальной величины равно мнимой части без знака “j” произведения комплекса амплитуды и оператора поворота :

.

Переход от одной формы записи синусоидальной величины к другой осуществляется с помощью формулы Эйлера:

,

(6)

Если, например, комплексная амплитуда напряжения задана в виде комплексного числа в алгебраической форме:

,

— то для записи ее в показательной форме, необходимо найти начальную фазу , т.е. угол, который образует вектор с положительной полуосью +1:

.

Тогда мгновенное значение напряжения:

,

где .

При записи выражения для определенности было принято, что , т.е. что изображающий вектор находится в первом или четвертом квадрантах. Если , то при (второй квадрант)

,

(7)

а при (третий квадрант)

(8)

(9)

Если задано мгновенное значение тока в виде , то комплексную амплитуду записывают сначала в показательной форме, а затем (при необходимости) по формуле Эйлера переходят к алгебраической форме:

.

Следует указать, что при сложении и вычитании комплексов следует пользоваться алгебраической формой их записи, а при умножении и делении удобна показательная форма.

Итак, применение комплексных чисел позволяет перейти от геометрических операций над векторами к алгебраическим над комплексами. Так при определении комплексной амплитуды результирующего тока по рис. 5 получим:

_где ;

.

Действующее значение синусоидальных ЭДС, напряжений и токов

В соответствии с выражением (3) для действующего значения синусоидального тока запишем:

.

Аналогичный результат можно получить для синусоидальных ЭДС и напряжений. Таким образом, действующие значения синусоидальных тока, ЭДС и напряжения меньше своих амплитудных значений в раз:

.

(10)

Поскольку, как будет показано далее, энергетический расчет цепей переменного тока обычно проводится с использованием действующих значений величин, по аналогии с предыдущим введем понятие комплекса действующего значения

.

1. Основы теории цепей: Учеб. для вузов /Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с.

2. Бессонов Л.А. Теоретические основы электротехники: Электрические цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с.

Контрольные вопросы и задачи

1. Какой практический смысл имеет изображение синусоидальных величин с помощью векторов?

2. Какой практический смысл имеет представление синусоидальных величин с использованием комплексных чисел?

3. В чем заключаются преимущества изображения синусоидальных величин с помощью комплексов по сравнению с их векторным представлением?

4. Для заданных синусоидальных функций ЭДС и тока записать соответствующие им комплексы амплитуд и действующих значений, а также комплексы мгновенных значений.

5. На рис. 5 , а . Определить .

Ответ: .