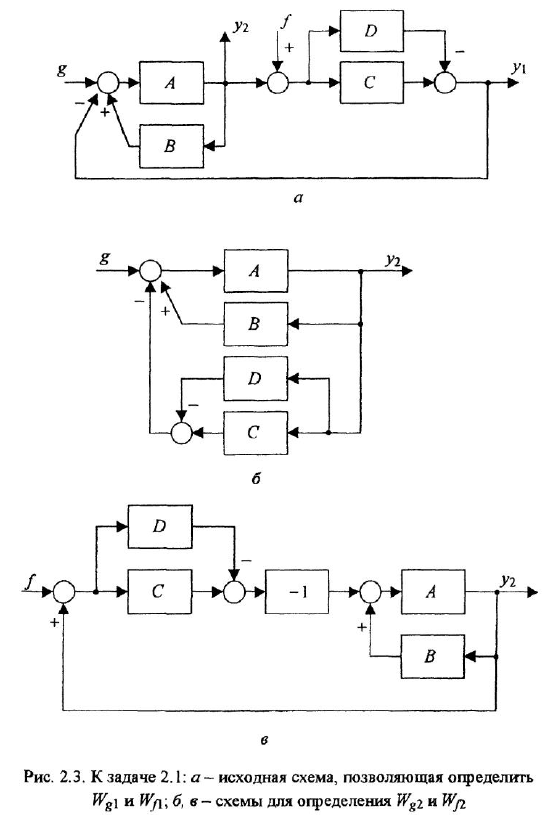
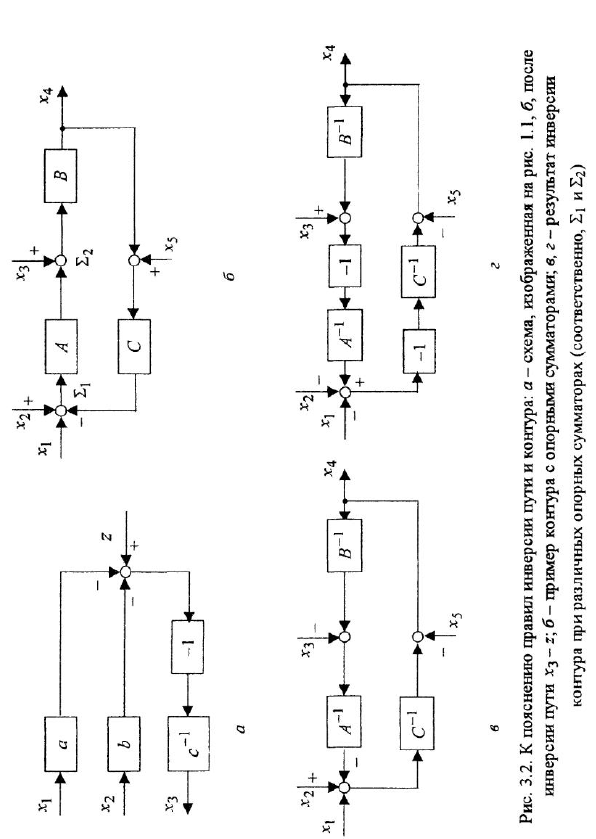
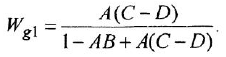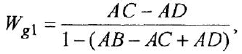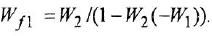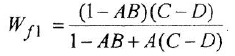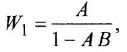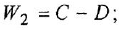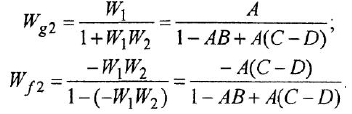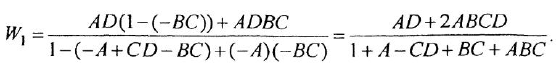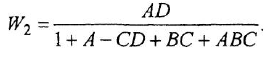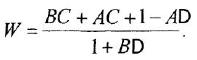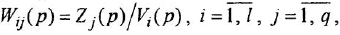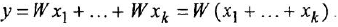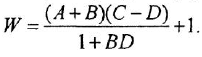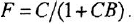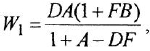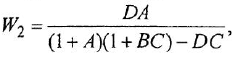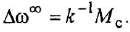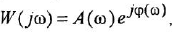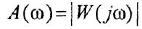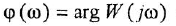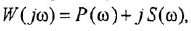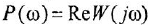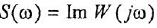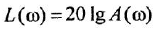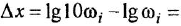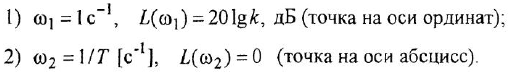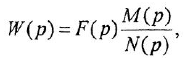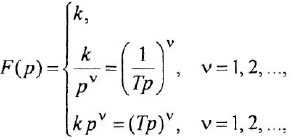Химические формулы для «чайников»
Структурные формулы — это просто!
Я думаю, что знакомство с формулами лучше всего начать со структурных формул органических веществ. Считается, что они сложны для понимания, поэтому в школе их изучают в выпускных классах. Но я уверен, что через 10 минут вы разберетесь, как легко составлять структурные формулы.
Перед нами структурная формула метана — самого простого органического вещества.
Что мы видим? В центре латинская буква C, а от неё четыре палочки, на концах которых четыре латинских буквы H. C означает углерод, а H — водород. Это два самых важных элемента, которые входят в состав любых органических веществ. А что означают палочки? Это химические связи. В них кроется практически весь секрет органической химии.
Фокус в том, что валентность углерода равна 4. Поэтому у каждой буквы C должно быть 4 палочки. А валентность водорода равна 1, поэтому у него палочка должна быть только одна.
По-моему, палочки отлично демонстрируют такие «страшные» понятия, как химические связи и валентность.
Структурные формулы могут слегка менять свой внешний вид. В них главное — количество элементов и наличие нужных связей. Например, формула метана может иметь и такой вид:
В общем, структурные формулы не являются какими-то жесткими конструкциями. Если вдруг Вам захотелось бы сделать модель молекулы из подручных материалов, то для этого лучше всего подошли бы шарики, соединённые пружинками или резинками. Под шариками я конечно подразумеваю атомы, а резинки — химические связи.
Но в химии приняты не только структурные формулы. И здесь мы познакомимся с некоторыми из них. Достаточно распространены так называемые истинные формулы. Для метана истинная формула записывается так:
Стоит упомянуть, что метан — это природный газ, который знаком всем, у кого есть газовая плита. Но не будем на нём долго задерживаться. Пора посмотреть, какие ещё бывают варианты органических структур.
Углеводороды
Прежде, чем мы начнём знакомство с многочисленными органическими соединениями, хочу напомнить — мы здесь изучаем химические формулы. А все упоминаемые вещества служат для иллюстрации.
| Вещество | Развёрнутая структурная формула | Упрощенная структурная формула | Брутто-формула | |||
|---|---|---|---|---|---|---|
| Этан | H-C-C-H; H|#2|H; H|#3|H | CH3-CH3 | Пропан | H-C-C-C-H; H|#2|H; H|#3|H; H|#4|H | CH3-CH2-CH3 | Бутан | H-C-C-C-C-H; H|#2|H; H|#3|H; H|#4|H; H|#5|H | CH3-CH2-CH2-CH3 | Пентан | H-C-C-C-C-C-H;H|#2|H;H|#3|H;H|#4|H;H|#5|H;H|#6|H | CH3-CH2-CH2-CH2-CH3 | Гексан | H-C-C-C-C-C-C-H;H|#2|H;H|#3|H;H|#4|H;H|#5|H;H|#6|H;H|#7|H |
| Вещество | Развёрнутая формула | Упрощённая формула | Брутто-фломула |
|---|---|---|---|
| Этен (Этилен) | $slope(55)H\C _(x1,N2)C /H | CH2=CH2 | |
| Пропен (Пропилен) | $slope(45)H\C-C/C/H; H\#-3\H;H/#2-#3\H | CH2=CH-CH3 | |
| Бутен (Бутилен) | H\C =C -C -C-H; H|#-3|H | CH2=CH-CH2-CH3 | |
| Этин (Ацетилен) | H-C%C-H | CH%CH | |
| Пропин (Метилацетилен) | H-C%C-C-H; H|#-3|H | CH%C-CH3 | |
| Бутин (Этилацетилен) | H-C%C-C -C-H; H|#-3|H | CH%C-CH2-CH3 |
Представленные здесь вещества тоже относятся к углеводородам. Если хорошенько присмотреться, то можно увидеть определённое сходство с веществами из первой таблицы. Названия формируются заменой буквы в конце названия: этан — этен — этин или пропан — пропен — пропин. Сходство не ограничивается названиями. Главное — одинаковое количество атомов углерода. А значит — одинаковое количество звеньев в цепи.
Различие кроется в наличии двойных и тройных связей. Углеводороды в первой таблице называются предельными. Это означает, что к ним больше ничего нельзя добавить. А во второй таблице представлены непредельные углеводороды. То есть, при определённых условиях к ним можно добавить по парочке атомов водорода.
Кроме того, появились дополнительные названия. Тут тоже нет ничего страшного. Верхние названия, которые без скобок — это научные названия. А в скобках даны традиционные названия, которые тоже довольно часто употребляются как в научной литературе, так и в быту.
Циклические углеводороды
Продолжим знакомство с формулами углеводородов. Они ещё не раскрыли нам всех своих секретов. Оказывается, что цепочки могут быть замкнутыми. То есть, атомы углерода соединяются друг с другом циклически.
| Вещество | Развёрнутая формула | Упрощённая формула | Брутто-формула |
|---|---|---|---|
| Циклопропан | $slope(60)H`/C`/C:a`/H; H\#C\C:b\H; H-#a-#b-H | H2C_(x1.4)CH2_q3CH2_q3 | |
| Циклобутан | H|C|C|H; H|C|C|H; H-#2-#6-H; H-#3-#7-H | H2C-CH2`|CH2`-H2C_#1 | |
| Циклопентан | C_(x1.1)C@:H2() @()_qC@H2()_qC@H2()_qC@H2()_q@H2() | H2C_(x1.4)CH2_qCH2_qCH2_qH2C_q | |
| Циклогексан | C\C@:H2() @()|C@H2()`/C@H2()`\C@H2()`|C@H2()/@H2() | $L(1.3)CH2\CH2|CH2`/CH2`\H2C`|H2C/ |
Изомеры
До сих пор мы не особенно обращали внимания на последнюю колонку, где выведены брутто-формулы. Но может возникнуть вполне законный вопрос: зачем вообще нужны структурные формулы? Ведь брутто-формулы гораздо проще записывать. Может быть, достаточно было бы пользоваться только ими?
Но оказывается, что без структурных формул обойтись не получится. Например, если сравнить брутто-формулы из двух предыдущих таблиц, то мы увидим, что циклопропан имеет абсолютно тот же состав, что и пропен ( C3H6 ). А брутто-формула циклобутана совпадает с бутеном ( C4H8 ). Но это разные вещества! И разница заключается в структуре. То есть, имеет большое значение, в каком порядке элементы соединены друг с другом. А значит, именно структурные формулы позволяют точно описать нужное вещество.
В химии существует такое понятие как изомеры. Так называют разные вещества, которые имеют одинаковый состав. Это не редкость. И в этом нет ничего странного. Ведь бывают же совершенно разные слова, состоящие из одинаковых букв.
Классическими изомерами среди углеводородов можно назвать бутан и изобутан. Посмотрим на их формулы:
| Вещество | Развёрнутая структурная формула | Упрощенная структурная формула | Брутто-формула | Бутан | H-C-C-C-C-H; H|#2|H; H|#3|H; H|#4|H; H|#5|H | CH3-CH2-CH2-CH3 | Метилпропан (Изобутан) | H\C\C/C/H; H|#2`/H; H|#4\H; H|#3|C|H; H/#-3\H | CH3-CH -CH3 |
|---|---|---|---|---|---|---|
| Вещество | Упрощённая формула | Брутто-формула |
|---|---|---|
| Пентан | CH3-CH2-CH2-CH2-CH3 | |
| 2-метилбутан (Изопентан) | CH3-CH -CH2-CH3 | |
| 2,2-диметилпропан (Неопентан) | CH3-C -CH3 |
А у вещества декан, имеющего формулу C10H22 , существует 75 изомеров. Но мы не будем их здесь рассматривать.
Обратите внимание, что научное название зависит от числа звеньев в прямой цепочке, а традиционное название просто учитывает количество атомов углерода в молекуле. Так получилось из-за того, что химики, которые только начинали исследовать углеводороды, первым делом научились определять состав веществ. То есть, сначала люди смогли получить лишь брутто-формулы. А из них невозможно понять, какова длина самой длинной цепочки. Поэтому названия учитывали общее число атомов углерода.
Затем наука дошла до того, что люди смогли исследовать структуру молекул, придумали структурные формулы и переименовали уже известные вещества в соответствии с новыми знаниями. Но старые названия уже успели прижиться и существуют до сих пор.
Бензол и скелетные формулы
Думаю, что пора познакомиться ещё с одним весьма примечательным представителем углеводородов. Это вещество называется бензол. Вот его формулы:
| Развёрнутая формула | Упрощённая формула | Скелетная формула | Брутто-формула |
|---|---|---|---|
| H|C\C|C `//C `\C `||C /\/H | H_(y.5)C\\CH|CH`//C `\HC`||HC/ | \\|`//`\`||/ |
Чем же этот бензол так примечателен? Дело в том, что это шестиугольное колечко входит в состав огромного числа органических веществ.
И вот на примере бензола предлагаю ознакомиться с ещё одним очень важным способом записи структурных формул — скелетными формулами.
Как видно из таблицы, скелетная формула бензола представляет собой правильный шестиугольник без каких-либо букв, зато изображения химических связей выглядят одинаково.
В общем, правила составления скелетных формул отличаются от уже знакомых нам развёрнутых всего двумя особенностями:
- Буквы C не пишутся. Предполагается, что каждый угол изображаемой геометрической фигуры содержит атом углерода.
- Буквы H тоже не пишутся. Если в углу сходятся меньше четырёх линий, то это означает, что все оставшиеся заняты водородом.
Конечно, скелетные формулы не так просты, как развёрнутые, но зато их гораздо легче записывать. Поэтому в органической химии это самый популярный вид формул. И мне кажется, Вам тоже будет несложно к ним привыкнуть.
Давайте посмотрим, как выглядят формулы других веществ, производных от бензола.
| Вещество | Развёрнутая формула | Скелетная формула | Смешанный вариант | Брутто-формула |
|---|---|---|---|---|
| Нафталин | C/C \\C |C `//C `\C`|`\\C `/C ||C \C/`/|H | /\\|`//`\`|`\\`/||\// | C10H8 | |
| Толуол | H|C|C\C|C `//C `\C `||C /\/H; H-#2-H | |\\|`//`\`||/ | CH3|\\|`//`\`||/ | |
| Кумол | H\C\C/C/H; H|#2|H; H|#4|H; H|#3|C\C|C `//C `\C `||C /\/H | \ |\\|`//`\`||/ | H3C\ |\\|`//`\`||/ |
Как видите, появился ещё и смешанный вариант. Опять какой-то новый вид формул? На этот раз уже нет. Просто иногда внутри одной формулы удобно сочетать различные способы.
А вот скелетная формула углеводорода, который называется коронен. Причём, другие варианты здесь уже использовать нет смысла.
Скелетные формулы существуют не только для циклических молекул. Понятно, что метан и этан имеют слишком мало узлов, поэтому для них не стоит пытаться использовать скелетные формулы. А вот какая-нибудь длинная молекула изображается довольно легко. Только не в виде прямой цепочки, а при помощи ломаной линии, ведь атомы углерода изображаются углами.
| Бутан | Бутен | Изобутан | Гексан |
| /\/ | //\/ | \|`|0/ | /\/\/ |
Трехмерные изображения
Иногда плоского изображения становится недостаточно. Поэтому для изображения трехмерных структурных формул используют особое изображение для химических связей:
Формулы с окружностью
Само собой, все они означают одно и то же. Но первые три отличаются только поворотом вокруг собственного центра. Тут нет ничего необычного, ведь молекулы не стоят на одном месте. А вот дальше мы видим кружок вместо трёх двойных связей. Причём, я намеренно изобразил все атомы водорода в последней формуле. Чтобы было хорошо видно, что каждый угол фактически лишился одной чёрточки. Их заменил кружок. Он как бы означает, что все двойные связи равномерно распределены внутри кольца.
Формулы бензола, где используется чередование одинарных и двойных связей называются формулами Кекуле в честь немецкого учёного, который внёс значительный вклад в исследование структуры бензола.
На самом деле, среди химиков нет единого мнения по поводу того, насколько правильно использование формул с кружком. Некоторые авторы категорически против. Но есть масса публикаций, где такая запись широко употребляется. Моя задача состоит в том, чтобы Вы узнали о существовании подобных формул и не удивлялись, увидев их.
Вот пара примеров записи уже для уже знакомых нам веществ:
| Нафталин: | /\|`/`\`|_o`\`/|\/_o | Толуол: | `/`-`\/-\_o-CH3 |
Знакомство с кислородом. Спирты
До сих пор мы знакомились со структурными формулами углеводородов, которые состоят только из углерода и водорода. Думаю, пора познакомиться с новым элементом — кислородом. Он обозначается латинской буквой O. Его валентнсть равна 2. То есть, каждая буква O в структурных формулах должна снабжаться двумя палочками.
Кислород — очень распространённый элемент на нашей планете. Он входит в состав большого количества органических и неорганических веществ. Но мы начнём знакомство с группы веществ, называемых спиртами:
| Вещество | Развёрнутая структурная формула | Упрощенная структурная формула | Скелетная формула | Брутто-формула |
|---|---|---|---|---|
| Метанол (метиловый спирт) | H-C-O-H; H|#C|H | CH3-OH | \OH | |
| Этанол (этиловый спирт) | H-C-C-O-H; H|#2|H; H|#3|H | CH3-CH2-OH | /\OH | |
| 1-Пропанол (пропиловый спирт) | H-C-C-C-O-H; H|#2|H; H|#3|H; H|#4|H | CH3-CH2-CH2-OH | /\/OH | |
| 2-Пропанол (изопропиловый спирт) | H-C-C-C-H; H|#2|H; H|#3|O|H; H|#4|H | CH3-CH -CH3 | \ / |
Не правда ли, что в этом есть что-то знакомое? Метан — метанол, этан — этанол, пропан — пропанол.
Да, можно сказать, что спирт получается из углеводорода, если заменить один атом -H на группу -O-H (или -OH в упрощенных структурных формулах). Химики называют её: гидроксильная группа, по латинским названиям водорода и кислорода. А иногда она даже называется спиртовой группой.
Все спирты можно описать в виде обобщённой формулы
Конечно же стоит упомянуть, что этанол — это тот самый спирт, который входит в состав алкогольных напитков. Другие представленные здесь спирты по запаху, цвету и даже вкусу довольно похожи на этиловый спирт. Но они очень вредны для здоровья человка. Например, один глоток метанола может оставить человека слепым на всю жизнь. А если выпить больше, то это можеть оказаться фатальным для жизни.
Ещё здесь из четырёх спиртов есть два изомера: 1-пропанол и 2-пропанол. У них одинаковые брутто-формулы, хотя вещества это разные. Их молекулы отличаются номером углеродного атома, к которому крепится группа OH. Возможно, Вы спросите, почему у 1-пропанола гидроксильная группа присоединена к третьему, а не к первому атому углерода? Тут следует вспомнить, что молекулы не находятся в одном положении. Они постоянно крутятся. И вполне могут развернуться как угодно:
Все спирты, с которыми мы уже успели познакомиться, имеют в своём составе одну гидроксильную группу. Химики называют их одноатомные спирты. Но существуют вещества с различным количеством гидроксильных групп. Они соответственно называются двухатомные спирты, трёхатомные спирты и так далее.
В качестве примера трёхатомного спирта можно привести достаточно известное вещество — глицерин:
| Развёрнутая формула | Упрощённая формула | Скелетная формула | Брутто-формула |
|---|---|---|---|
| H-C-C-C-H; $slope(45)H`/O|#2|H; H`/O|#3|H; H`/O|#4|H | OH|CH2-CH -CH2`|OH | HO\/ \/OH |
Ну и чтобы завершить знакомство со спиртами, приведу ещё формулу другого известного вещества — холестерина. Далеко не все знают, что он является одноатомным спиртом!
Карбоновые кислоты
Любой винодел знает, что вино должно храниться без доступа воздуха. Иначе оно скиснет. Но химики знают причину — если к спирту присоединить ещё один атом кислорода, то получится кислота.
Посмотрим на формулы кислот, которые получаются из уже знакомых нам спиртов:
| Вещество | Развёрнутая структурная формула | Упрощенная структурная формула | Скелетная формула | Брутто-формула |
|---|---|---|---|---|
| Метановая кислота (муравьиная кислота) | H/C`|O|\OH | HCOOH | O//\OH | |
| Этановая кислота (уксусная кислота) | H-C-C \O-H; H|#C|H | CH3-COOH | /`|O|\OH | |
| Пропановая кислота (метилуксусная кислота) | H-C-C-C \O-H; H|#2|H; H|#3|H | CH3-CH2-COOH | \/`|O|\OH | |
| Бутановая кислота (масляная кислота) | H-C-C-C-C \O-H; H|#2|H; H|#3|H; H|#4|H | CH3-CH2-CH2-COOH | /\/`|O|\OH | |
| Обобщённая формула |
Отличительной особенностью органических кислот является наличие карбоксильной группы (COOH), которая и придаёт таким веществам кислотные свойства.
Все, кто пробовал уксус, знают что он весьма кислый. Причиной этого является наличие в нём уксусной кислоты. Обычно столовый уксус содержит от 3 до 15% уксусной кислоты, а остальное (по большей части) — вода. Употребление в пищу уксусной кислоты в неразбавленном виде представляет опасность для жизни.
Карбоновые кислоты могут иметь несколько карбоксильных групп. В этом случае они называются: двухосновная, трёхосновная и т.д.
В пищевых продуктах содержится немало других органических кислот. Вот только некоторые из них:
| Щавелевая кислота | Молочная кислота | Яблочная кислота | Лимонная кислота |
| HOOC-COOH | H3C\ /COOH | HOOC\/ \COOH | HOOC\/ \/COOH |
| двухосновная карбоновая кислота | оксикарбоновая кислота | Двухосновная оксикарбоновая кислота | Трёхосновная оксикарбоновая кислота |
Название этих кислот соответствует тем пищевым продуктам, в которых они содержатся. Кстати, обратите внимание, что здесь встречаются кислоты, имеющие и гидроксильную группу, характерную для спиртов. Такие вещества называются оксикарбоновыми кислотами (или оксикислотами).
Внизу под каждой из кислот подписано, уточняющее название той группы органических веществ, к которой она относится.
Радикалы
Радикалы — это ещё одно понятие, которое оказало влияние на химические формулы. Само слово наверняка всем известно, но в химии радикалы не имеют ничего общего с политиками, бунтовщиками и прочими гражданами с активной позицией.
Здесь это всего лишь фрагменты молекул. И сейчас мы разберёмся, в чём их особенность и познакомимся с новым способом записи химических формул.
Выше по тексту уже несколько раз упоминались обобщённые формулы: спирты —
Если выражаться более определённо, то одновалентным радикалом называется часть молекулы, лишённая одного атома водорода. Ну а если отнять два атома водорода, то получится двухвалентный радикал.
Радикалы в химии получили собственные названия. Некоторые из них получили даже латинские обозначения, похожие на обозначения элементов. И кроме того, иногда в формулах радикалы могут быть указаны в сокращённом виде, больше напоминающем брутто-формулы.
Всё это демонстрируется в следующей таблице.
| Название | Структурная формула | Обозначение | Краткая формула | Пример спирта | ||
|---|---|---|---|---|---|---|
| Метил | CH3-<> | Me | CH3 | CH3OH | ||
| Этил | CH3-CH2-<> | Et | C2H5 | C2H5OH | ||
| Пропил | CH3-CH2-CH2-<> | Pr | C3H7 | C3H7OH | ||
| Изопропил | H3C\CH(*`/H3C*)-<> | i-Pr | C3H7 | (CH3)2CHOH | ||
| Фенил | `/`=`\//-\\-<> | Ph | C6H5 | C6H5OH | ||
Думаю, что здесь всё понятно. Хочу только обратить внимание на колонку, где приводятся примеры спиртов. Некоторые радикалы записываются в виде, напоминающем брутто-формулу, но функциональная группа записывается отдельно. Например, CH3-CH2-OH превращается в C2H5OH .
А для разветвлённых цепочек вроде изопропила применяются конструкции со скобочками.
Существует ещё такое явление, как свободные радикалы. Это радикалы, которые по каким-то причинам отделились от функциональных групп. При этом нарушается одно из тех правил, с которых мы начали изучение формул: число химических связей уже не соответствует валентности одного из атомов. Ну или можно сказать, что одна из связей становится незакрытой с одного конца. Обычно свободные радикалы живут короткое время, ведь молекулы стремятся вернуться в стабильное состояние.
Знакомство с азотом. Амины
Предлагаю познакомиться с ещё одним элементом, который входит в состав многих органических соединений. Это азот.
Он обозначается латинской буквой N и имеет валентность, равную трём.
Посмотрим, какие вещества получаются, если к знакомым нам углеводородам присоединить азот:
| Вещество | Развёрнутая структурная формула | Упрощенная структурная формула | Скелетная формула | Брутто-формула |
|---|---|---|---|---|
| Аминометан (метиламин) | H-C-N \H;H|#C|H | CH3-NH2 | \NH2 | |
| Аминоэтан (этиламин) | H-C-C-N \H;H|#C|H;H|#3|H | CH3-CH2-NH2 | /\NH2 | |
| Диметиламин | H-C-N -C-H; H|#-3|H; H|#2|H | $L(1.3)H/N \dCH3 | /N \ | |
| Аминобензол (Анилин) | H\N |C\\C |C `//C `\C `||C / | NH2|C\\CH|CH`//C `\HC`||HC/ | NH2|\|`/`\`|/_o | |
| Триэтиламин | $slope(45)H-C-C/N\C-C-H;H|#2|H; H|#3|H; H|#5|H;H|#6|H; #N`|C `|C `|H | CH3-CH2-N -CH2-CH3 | \/N \| |
Как Вы уже наверное догадались из названий, все эти вещества объединяются под общим названием амины. Функциональная группа <>-NH2 называется аминогруппой. Вот несколько обобщающих формул аминов:
| По числу замещённых атомов водорода | По числу аминогрупп в молекуле |
|---|---|
| Первичный амин | Моноамин |
Вторичный амин | Диамин H2N- | |
Третичный амин | Триамин H2N- | |
В общем, никаких особых новшеств здесь нет. Если эти формулы Вам понятны, то можете смело заниматься дальнейшим изучением органической химии, используя какой-нибудь учебник или интернет.
Но мне бы хотелось ещё рассказать о формулах в неорганической химии. Вы убедитесь, как их легко будет понять после изучения строения органических молекул.
Рациональные формулы
Не следует делать вывод о том, что неорганическая химия проще, чем органическая. Конечно, неорганические молекулы обычно выглядят гораздо проще, потому что они не склонны к образованию таких сложных структур, как углеводороды. Но зато приходится изучать более сотни элементов, входящих в состав таблицы Менделеева. А элементы эти имеют склонность объединяться по химическим свойствам, но с многочисленными исключениями.
Так вот, ничего этого я рассказывать не буду. Тема моей статьи — химические формулы. А с ними как раз всё относительно просто.
Наиболее часто в неорганической химии употребляются рациональные формулы. И мы сейчас разберёмся, чем же они отличаются от уже знакомых нам.
Для начала, познакомимся с ещё одним элементом — кальцием. Это тоже весьма распространённый элемент.
Обозначается он Ca и имеет валентность, равную двум. Посмотрим, какие соединения он образует с известными нам углеродом, кислородом и водородом.
| Вещество | Структурная формула | Рациональная формула | Брутто-формула |
|---|---|---|---|
| Оксид кальция | Ca=O | CaO | |
| Гидроксид кальция | H-O-Ca-O-H | Ca(OH)2 | |
| Карбонат кальция | $slope(45)Ca`/O\C|O`|/O`\#1 | CaCO3 | |
| Гидрокарбонат кальция | HO/`|O|\O/Ca\O/`|O|\OH | Ca(HCO3)2 | |
| Угольная кислота | H|O\C|O`|/O`|H | H2CO3 |
При первом взгляде можно заметить, что рациональная формула является чем то средним между структурной и брутто-формулой. Но пока что не очень понятно, как они получаются. Чтобы понять смысл этих формул, нужно рассмотреть химические реакции, в которых участвуют вещества.
Кальций в чистом виде — это мягкий белый металл. В природе он не встречается. Но его вполне возможно купить в магазине химреактивов. Он обычно хранится в специальных баночках без доступа воздуха. Потому что на воздухе он вступает в реакцию с кислородом. Собственно, поэтому он и не встречается в природе.
Итак, реакция кальция с кислородом:
Но и гидроксид кальция не встречается в природе из-за наличия в воздухе углекислого газа. Думаю, что все слыхали про этот газ. Он образуется при дыхании людей и животных, сгорании угля и нефтепродуктов, при пожарах и извержениях вулканов. Поэтому он всегда присутствует в воздухе. Но ещё он довольно хорошо растворяется в воде, образуя угольную кислоту:
Таким образом, гидроксид кальция, растворённый в воде, вступает в реакцию с угольной кислотой и превращается в малорастворимый карбонат кальция:
Из карбоната кальция в значительной степени состоят мел, известняк, мрамор, туф и многие другие минералы. Так же он входит в состав кораллов, раковин моллюсков, костей животных и т.д.
Но если карбонат кальция раскалить на очень сильном огне, то он превратится в оксид кальция и углекислый газ.
Этот небольшой рассказ о круговороте кальция в природе должен пояснить, для чего нужны рациональные формулы. Так вот, рациональные формулы записываются так, чтобы были видны функциональные группы. В нашем случае это:
| OH | Гидроксильная группа |
| CO3 | Карбонат — соль угольной кислоты |
| HCO3 | Гидрокарбонат — кислая соль угольной кислоты |
Кроме того, отдельные элементы — Ca, H, O(в оксидах) — тоже являются самостоятельными группами.
Думаю, что пора знакомиться с ионами. Это слово наверняка всем знакомо. А после изучения функциональных групп, нам ничего не стоит разобраться, что же представляют собой эти ионы.
В общем, природа химических связей обычно заключается в том, что одни элементы отдают электроны, а другие их получают. Электроны — это частицы с отрицательным зарядом. Элемент с полным набором электронов имеет нулевой заряд. Если он отдал электрон, то его заряд становится положительным, а если принял — то отрицатеньным. Например, водород имеет всего один электрон, который он достаточно легко отдаёт, превращаясь в положительный ион. Для этого существует специальная запись в химических формулах:
Отрицательно заряженные ионы называются анионы. Обычно к ним относятся кислотные остатки.
Положительно заряженные ионы — катионы. Чаще всего это водород и металлы.
И вот здесь наверное можно полностью понять смысл рациональных формул. В них сначала записывается катион, а за ним — анион. Даже если формула не содержит никаких зарядов.
Вы наверное уже догадываетесь, что ионы можно описывать не только рациональными формулами. Вот скелетная формула гидрокарбонат-аниона:
Система Хилла
Итак, можно считать, что мы уже изучили структурные и рациональные формулы. Но есть ещё один вопрос, который стоит рассмотреть подробнее. Чем же всё-таки отличаются брутто-формулы от рациональных?
Мы знаем почему рациональная формула угольной кислоты записывается H2CO3 , а не как-то иначе. (Сначала идут два катиона водорода, а за ними карбонат-анион). Но почему брутто-формула записывается CH2O3 ?
В принципе, рациональная формула угольной кислоты вполне может считаться истинной формулой, ведь в ней нет повторяющихся элементов. В отличие от NH4OH или Ca(OH)2 .
Но к брутто-формулам очень часто применяется дополнительное правило, определяющее порядок следования элементов. Правило довольно простое: сначала ставится углерод, затем водород, а дальше остальные элементы в алфавитном порядке.
Вот и выходит CH2O3 — углерод, водород, кислород. Это называется системой Хилла. Она используется практически во всех химических справочниках. И в этой статье тоже.
Немного о системе easyChem
Вместо заключения мне хотелось бы рассказать о системе easyChem. Она разработана для того, чтобы все те формулы, которые мы тут обсуждали, можно было легко вставить в текст. Собственно, все формулы в этой статье нарисованы при помощи easyChem.
Зачем вообще нужна какая-то система для вывода формул? Всё дело в том, что стандартный способ отображения информации в интернет-браузерах — это язык гипертекстовой разметки (HTML). Он ориентирован на обработку текстовой информации.
Рациональные и брутто-формулы вполне можно изобразить при помощи текста. Даже некоторые упрощённые структурные формулы тоже могут быть записаны текстом, например спирт CH3-CH2-OH . Хотя для этого пришлось бы в HTML использовать такую запись: CH3-CH2-OH .
Это конечно создаёт некоторые трудности, но с ними можно смириться. Но как изобразить структурную формулу? В принципе, можно использовать моноширинный шрифт:
Выглядит конечно не очень красиво, но тоже осуществимо.
Настоящая проблема возникает при попытке изобразить бензольные кольца и при использовании скелетных формул. Здесь не остаётся иного пути, кроме подключения растрового изображения. Растры хранятся в отдельных файлах. Браузеры могут подключать изображения в формате gif, png или jpeg.
Для создания таких файлов требуется графический редактор. Например, Фотошоп. Но я более 10 лет знаком с Фотошопом и могу сказать точно, что он очень плохо подходит для изображения химических формул.
Гораздо лучше с этой задачей справляются молекулярные редакторы. Но при большом количестве формул, каждая из которых хранится в отдельном файле, довольно легко в них запутаться.
Например, число формул в этой статье равно . Из них выведены виде графических изображений (остальные при помощи средств HTML).
Система easyChem позволяет хранить все формулы прямо в HTML-документе в текстовом виде. По-моему, это очень удобно.
Кроме того, брутто-формулы в этой статье вычисляются автоматически. Потому что easyChem работает в два этапа: сначала текстовое описание преобразуется в информационную структуру (граф), а затем с этой структурой можно выполнять различные действия. Среди них можно отметить следующие функции: вычисление молекулярной массы, преобразование в брутто-формулу, проверка на возможность вывода в виде текста, графическая и текстовая отрисовка.
Таким образом, для подготовки этой статьи я пользовался только текстовым редактором. Причём, мне не пришлось думать, какая из формул будет графической, а какая — текстовой.
Вот несколько примеров, раскрывающих секрет подготовки текста статьи:
| Текстовое описание easyChem | Выводимый результат | Сгенерированная брутто-формула |
|---|---|---|
| (NH4)2CO3 | (NH4)2CO3 | |
| H-C-C-O-H; H|#2|H; H|#3|H | H-C-C-O-H; H|#2|H; H|#3|H | |
| CH3|\\|`//`\`||/ | CH3|\\|`//`\`||/ |
Описания из левого столбца автоматически превращаются в формулы во втором столбце.
В первой строчке описание рациональной формулы очень похоже на отображаемый результат. Разница только в том, что числовые коэффициенты выводятся подстрочником.
Во второй строке развёрнутая формула задана в виде трёх отдельных цепочек, разделённых символом ; Я думаю, нетрудно заметить, что текстовое описание во многом напоминает те действия, которые потребовались бы для изображения формулы карандашом на бумаге.
В третьей строке демонстрируется использование наклонных линий при помощи символов \ и /. Значок ` (обратный апостроф) означает, что линия проводится справа налево (или снизу вверх).
Здесь есть гораздо более подробная документация по использованию системы easyChem.
На этом разрешите закончить статью и пожелать удачи в изучении химии.
Как решать химические уравнения — схемы и примеры решения для разных реакций
Основные термины и понятия
Составление уравнений химических реакций невозможно без знания определённых обозначений, показывающих, как проходит реакция. Объединение атомов, имеющих одинаковый ядерный заряд, называют химическим элементом. Ядро атома состоит из протонов и нейтронов. Первые совпадают с числом атомного номера элемента, а значение вторых может варьироваться. Простейшими веществами называют элементы, состоящие из однотипных атомов.
Любой химический элемент описывается с помощью символов, условно обозначающих структуру веществ. Формулы являются неотъемлемой частью языка науки. Именно на их основе составляют уравнения и схемы. По своей сути они отражают количественный и качественный состав элементов. Например, запись HNO3 сообщает, что в соединении содержится одна молекула азотной кислоты, а оно само состоит из водорода, азота и кислорода. При этом в состав одного моля азотной кислоты входит по одному атому водорода и азота и 3 кислорода.
Символика элементов, условное обозначение, представляет собой химический язык. В значке содержится информация о названии, массовом числе и порядковом номере. Международное обозначение принято, согласно периодической таблице Менделеева, разработанной в начале 1870 года.
Взаимодействующие между собой вещества называются реагентами, а образующиеся в процессе реакции — продуктами. Составление и решение химических уравнений фактически сводится к определению результатов реакций, поэтому просто знать формулы веществ мало, нужно ещё уметь подбирать коэффициенты. Располагаются они перед формулой и указывают на количество молекул или атомов, принимающих участие в процессе. С правой стороны от химического вещества ставится индекс, указывающий место элемента в системе.
Записывают уравнения в виде цепочки, в которой указываются все стадии превращения вещества начиная с левой части. Вначале пишут формулы элементов в исходном состоянии, а затем последовательно их преобразование.
Виды химических реакций
Химические явления характеризуются тем, что из двух и более элементов образуются новые вещества. Уравнения описывают эти процессы. Впервые с объяснениями протекания реакций знакомят в восьмом классе средней образовательной школы на уроках неорганической химии. Ученикам демонстрируют опыты, в которых явно наблюдаются различия в протекании реакций.
Всего существует 4 типа химического взаимодействия веществ:
- Соединение. В реакцию могут вступать 2 простых вещества: металл и неметалл или неметалл и неметалл. Например, алюминий с серой образуют сульфид алюминия. Кислород, взаимодействуя с водородом, превращается в воду. Объединятся могут 2 оксида с растворимым основанием, как оксид кальция с водой: CaO + H2O = Ca (OH)2 или основной оксид с кислотным: CaO + SO3 = CaSO4.
- Разложение. Это процесс обратный реакции соединения: было одно вещество, а стало несколько. Например, при пропускании электрического тока через воду получается водород и кислород, а при нагревании известняка 2 оксида: CaCO3 = CaO + CO2.
- Замещение. В реакцию вступают 2 элемента. Один из них простой, а второй сложный. В итоге образуются 2 новых соединения, при котором атом простого вещества заменяет сложный, как бы вытесняя его. Условие протекания процесса: простое вещество должно быть более активным, чем сложное. Например, Zn + 2HCl = ZnCl2 + H2. Величину активности можно узнать из таблицы ряда электрохимических напряжений.
- Обмен. В этом случае между собой реагируют 2 сложных элемента, обменивающиеся своими составными частями. Условием осуществления такого типа реакции является обязательное образование воды, газа или осадка. Например, CuO + 2HCl = CuCl2 + H2O. Чтобы узнать, смогут ли вещества прореагировать, используют таблицу растворимости.
Основными признаками химических реакций является изменение цвета, выделение газа или образование осадка. Различают их по числу веществ, вступивших в реакцию и образовавшихся продуктов. Правильное определение типа реакции особо важно при составлении химических уравнений, а также определения свойств и возможностей веществ.
Окислительно-восстановительный процесс
Составление большинства реакций сводится к подбору коэффициентов. Но при этом могут возникнуть трудности с установлением равновесия, согласно закону сохранения массы веществ. Чаще всего такая ситуация возникает при решении заданий, связанных с расстановкой количества атомов в уравнениях окислительно-восстановительных процессов.
Под ними принято понимать превращения, протекающие с изменением степени окисления элементов. При окислении происходит процесс передачи атомом электронов, сопровождающийся приобретением им положительного заряда или ионом, после чего он становится нейтральным. При этом также происходит процесс восстановления, связанный с присоединением элементарных частиц атомом.
Для составления уравнений необходимо определить восстановитель, окислитель и число участвующих в реакции электронов. Коэффициенты же подбирают с помощью метода электронно-ионного баланса (полуреакций). Его суть состоит в установлении равенства путём уравнивания количества электронов, отдаваемых одним элементом и принимаемым другим.
Классический алгоритм
В основе решения задач этим методом — закон сохранения массы. Согласно ему, совокупная масса элементов до реакции и после остаётся неизменной. Другими словами, происходит перегруппировка частиц. Если рассматривать решение химического уравнения поэтапно, оно будет состоять из трёх шагов:
- Написания формул элементов, вступающих в реакцию с левой стороны.
- Указания справа формулы образующихся веществ.
- Уравнивания числа атомов с добавлением коэффициентов.
Перед тем как переходить к сложным соединениям, лучше всего потренироваться на простых. Например, нужно составить уравнение, описывающее взаимодействие двух сложных веществ: гидроксида натрия и серной кислоты. При таком соединении образуется сульфат натрия и вода.
Согласно алгоритму, в левой части уравнения необходимо записать реагенты, а в правой продукты реакции: NaOH + H2SO 4 → Na 2SO4 + H2O. Теперь следует уравнять коэффициенты. Начинают с первого элемента. В примере это натрий. В правой части содержится 2 его атома, а в левой один, поэтому необходимо возле реагента поставить цифру 2. Затем нужно уровнять водород. В результате получится выражение: 2 NaOH + H2SO 4 → Na2 SO4 +2H2O.
Ещё одним наглядным примером является процесс реакции тринитротолуола с кислородом. При их взаимодействии образуется: C7H5N3O6 + O2 → CO2 + H2O + N2. Исходя из того, что слева находится нечётное число атомов H и N, а справа чётное, нужно их уравнять: 2C7H5N3O6 + O2 → CO2 + H2O + N2.
Теперь становится понятным, что 14 и 10 атомов углерода и водорода должны образовать 14 долей диоксида и 5 молекул воды. При этом 6 атомов азота превратятся в 3. Итоговое уравнение будет выглядеть как 2C7H5N3O6 + 10,5O2 → 14CO2 + 5H2O + 3N2.
Перед тем как начинать тренировку по составлению уравнений, следует научиться расставлять валентность. Это параметр, равный числу соединившихся атомов каждого элемента. Фактически это способность к соединению. Например, в формуле NH3 валентность атома азота равна 3, а водорода 1.
Решение методом полуреакций
Алгоритм для решения примеров химических уравнений проще рассмотреть на конкретном задании. Пускай необходимо описать процесс окисления пирита азотной кислоты с малой концентрацией: FeS2 + HNO3. Решать этот пример необходимо в следующей последовательности:
- Определить продукты реакции. Так как кислота является сильным окислителем, сера получит максимальную степень оксидации S6+, а железо Fe3+. HNO3 может восстановиться до одного из двух состояний NO2 или NO.
- Исходя из состава ионов и правила, что вещества, переходящие в газовую форму или плохо растворимые, записываются в молекулярном виде, верным будет записать: FeS2 — Fe3+ + 2SO2−4. Гидролизом можно пренебречь.
- В записи уравнивают кислород. Для этого в левую часть добавляют 8 молекул воды, а в правую 16 ионов водорода: FeS2 + 8H20 — Fe3+ + 2SO2−4 + 16H+. Так как заряда в левой части нет, а в правой он равный +15, то серное железо должно будет отдать 15 электронов. Значит, уравнение примет вид: FeS2 + 8H20 — 15e → Fe3+ + 2SO2−4 + 16H+.
- Теперь переходят к реакции восстановления нитрата иона: NO-3 →NO. Для её составления нужно отнять у оксида азота 2 атома кислорода. Делают это путём прибавления к левой части 4 ионов водорода, а правой — 2 молекул воды. В итоге получится: NO-3 + 4H+ → NO + 2H2O.
- Полученную формулу уравнивают добавлением к левой части 3 электронов: NO-3 + 4H+ 3e → NO + 2H2O.
- Объединяют найденные выражения и записывают результат: FeS2 + 8H20 + 5NO-3 + 20H+ → Fe3+ + 2SO2−4 + 16H+ + 5NO + 10H2O.
Уравнение можно сократить на 16H + и 8H2O. В итоге получится сокращённое выражение окислительно-восстановительной реакции: FeS2 + 5NO — 3 + 4 H + = Fe3 + + 2SO 2- 4 + 5NO + 2H2O.
Такой алгоритм считается классическим, но для упрощения понимания лучше использовать способ электронного баланса. Процесс восстановления переписывают как N5+ + 3e → N2+. Степень же окисления составить сложнее. Сере нужно приписать степень 2+ и учесть, что на 1 атом железа приходится 2 атома серы: FeS2 → Fe3++ 2S6+. Запись общего баланса будет выглядеть: FeS2 + 5N5+ = Fe3+ + 2S6+ + 5N2+.
Пять молекул потратятся на окисление серного железа, а ещё 3 на образование Fe (NO3)3. После уравнения двух сторон запись реакции примет вид, аналогичный полученному с использованием предыдущего метода.
Использование онлайн-расчёта
Простые уравнения решать самостоятельно довольно просто. Но состоящие из сложных веществ могут вызвать трудности даже у опытных химиков. Чтобы получить точную формулу и не подбирать вручную коэффициенты, можно воспользоваться онлайн-калькуляторами. При этом их использовать сможет даже пользователь, не особо разбирающийся в науке.
Чтобы расстановка коэффициентов в химических уравнениях онлайн происходила автоматически, нужно лишь подключение к интернету и исходные данные. Система самостоятельно вычислит продукты реакции и уравняет обе стороны формулы. Интересной особенностью таких сайтов является не только быстрый и правильный расчёт, но и описание правил с алгоритмами, по которому выполняются действия.
После загрузки калькулятора в веб-обозревателе единственное, что требуется от пользователя — правильно ввести реагенты в специальные формы латинскими буквами и нажать кнопку «Уравнять». Иногда возникает ситуация, когда запись сделана верно, но коэффициенты не расставляются. Это происходит, если суммы в уравнении могут быть подсчитаны разными способами. Характерно это для реакций окисления. В таком случае нужно заменить фрагменты молекул на любой произвольный символ. Таким способом можно не только рассчитать непонятное уравнение, но и выполнить проверку своих вычислений.
Примеры решения задач по ТАУ
Здравствуйте на этой странице я собрала теорию и практику с примерами решения задач по предмету теория автоматического управления с решением по каждой теме, чтобы вы смогли освежить знания!
| Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу! |
ТАУ
Теория автоматического управления является основной общепрофессиональной дисциплиной направления подготовки дипломированного специалиста «Автоматизированные технологии и производства».
Основной целью автоматизации является исключение непосредственного участия человека в управлении производственными процессами и другими техническими объектами.
В настоящее время автоматизация технологических процессов представляет собой одно из важнейших средств роста эффективности производства, интенсификации развития народного хозяйства. Таким образом, задача изучения дисциплины «Теория автоматического управления» состоит в освоении основных принципов построения и функционирования автоматических систем управления на базе современных математических методов и технических средств.
Построение структурных схем и сигнальных графов автоматических систем
В теории систем автоматического управления (САУ) широко используют понятие звена, под которым понимают некоторый физический элемент системы (усилитель, двигатель, датчик и т. п.) либо формально выделенную часть математической модели системы (например, уравнение равновесия напряжений якорной цепи двигателя), для которых указаны входные (одна или несколько) и выходная (обычно одна) переменные. При этом говорят, что звено преобразует входные переменные, т. е. приложенные к звену внешние воздействия, в выходную переменную — реакцию. В математическом плане обобщением понятий САУ и звена САУ является понятие динамической системы.
Возможно эта страница вам будет полезна:
Дифференциальное уравнение (ДУ) линейной динамической системы с одним входом и одним выходом записывается в классической форме следующим образом:
Здесь 
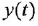
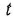
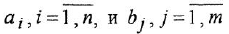
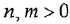
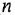
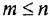
полиномы степеней, соответственно, 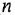
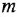
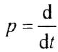
Определим формально операторную передаточную функцию (ОПФ) 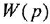
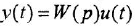
Преобразование ДУ (1.1) по Лапласу при нулевых начальных условиях (ННУ) дает
(использована теорема об изображении производной при ННУ: если
a 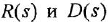
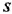
Передаточной функцией (ПФ) 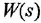
Отсюда в силу уравнения (1.4) и с учетом (1.3) получаем:
т. е. ПФ совпадает с ОПФ с точностью до обозначения аргумента
В связи с этим в дальнейшем будем использовать одно и го же обозначение, например 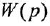
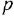
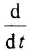
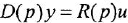
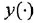
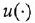
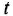
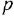
С учетом сказанного рекомендуется следующая методика нахождения ПФ поДУ( 1.1), не требующая применения преобразования Лапласа:
- Заменить в уравнении (1.1)
на
и представить это уравнение в форме (1.2).
- Перейти из временной области в комплексную, просто заменив
и
на
и
.
- Найти ПФ как
.
Если система имеет несколько входов и/или выходов, т. е. является многомерной, то уместно говорить о множестве передаточных функций, связывающих каждый вход 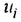
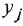
Все они имеют один и тот же знаменатель (если не производить сокращения одинаковых нулей и полюсов) и, в общем случае, разные числители:
Теперь приведем передаточные функции наиболее важных типовых звеньев систем автоматического управления. 1 Пропорциональное звено:
где 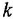
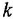
где 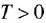
В качестве обобщения можно рассматривать интегрирующее звено произвольного порядка:
- Дифференцирующее звено:
Обобщенное дифференцирующее звено:
где 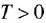
- Апериодическое звено 2-го порядка:
где 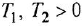
где 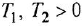
где 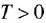
Часто в передаточных функциях звеньев 4, 6, 7 и 8 вместо единицы пишут коэффициент передачи к.
Построение структурных схем и М-графов динамических систем
При анализе и синтезе систем автоматического управления часто прибегают к графическом)’ изображению уравнений, описывающих систему. Для этой цели обычно используют структурные схемы и, реже, сигнальные графы В структурной схеме переменные обозначаются отрезками прямых или ломаными линиями, оканчивающимися стрелками В графе каждой переменной соответствует некоторая вершина. Мы будем рассматривать только одну разновидность сигнальных графов, а именно граф Мейсона (Мэзона), или, короче, М-граф
Уравнение звена вила 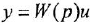
В вершину графа могут входить несколько дуг. В этом случае действует следующее соглашение: переменная, отождествляемая с вершиной, в которую входят дуги, равна взвешенной сумме переменных, соответствующих вершинам, из которых эти дуги исходят, причем в качестве весовых коэффициентов выступают передачи дуг. Так, М-граф, приведенный на рис. 11,6, соответствует уравнению 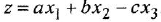
Часто одна и та же переменная входит в несколько уравнений Чтобы в структурной схеме иметь возможность использовать какую-либо переменную в качестве входа сразу нескольких звеньев, применяют специализированный элемент — отвод. Это линия, отходящая от основной в какой-либо точке и обозначающая ту же переменную, что и основная линия (см. рис. 1.1, в, где показаны два отвода). Начало отвода отмечается «жирной» точкой.
Если в структурной схеме имеется горизонтальная цепочка звеньев, чередующихся с сумматорами, то обычно знаки «плюс» или «минус» ставят не у всех стрелок, входящих в сумматоры, а только у тех, которые подходят к данной цепочке извне (см., например, три сумматора между переменными 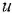
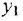
Пусть система задана некоторым числом алгебраических и дифференциальных уравнений. Чтобы построить по ним структурную схему и М-граф системы, рекомендуется выполнить следующие действия:
- В дифференциальных уравнениях заменить
переменной
.
- Полагая, что каждому уравнению соответствует некоторое звено системы, назначить для него выходную и входные переменные При этом часто удобно руководствоваться физическими соображениями и представлениями о причинно-следственных связях между неременными Например, если речь идет об уравнении электрической или электромагнитной цепи, то естественно считать входной величиной напряжение (ЭДС) источника, а выходной — ток. Для уравнения механического вращательного движения входными переменными будут движущий момент и момент сопротивления, а выходной — угловая скорость.
- В каждом уравнении (уравнении
-го звена) выразить выходную переменную
— через входные
(
— число входов):
При этом выражения 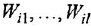
- По каждому уравнению вида (1.15) изобразить М-граф, для чего:
а) нанести на рисунок вершины, соответствующие переменным 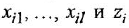
б) из каждой вершины 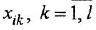
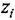
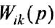
Поскольку правая часть уравнения (1.15) представляет собой алгебраическую сумму, для изображения соответствующей структурной схемы необходим сумматор. В результате получается схема, подобная той, что показана на рис. 11, б Таким образом, если звено имеет один вход, то ему соответствуют структурная схема и М-граф аналогичные тем, что приведены на рис. 1.1, в Нел и же входов несколько, то звену (уравнению) соответствует структурная схема и граф, содержащие несколько звеньев (дуг), причем в структурной схеме обязательно появится сумматор
Уравнения, по которым строится структурная схема или граф, связаны между собой, так как содержат общие переменные Это должно быть ясно отражено и в самой схеме (графе), а именно: в графе не должно быть двух вершин с одинаковыми именами переменных, а в структурной схеме линии, соответствующие одной и той же переменной, должны либо совпадать (так что выход одного звена является входом другого), либо выступать одна по отношению к другой как основная линия и отвод.
Нецелесообразно изображать систему исходных уравнений в виде набора отдельных фрагментов структурной схемы: после этого все равно придется проводить между ними линии связи.
Удобнее рисовать схему (граф) последовательно, используя то обстоятельство, что входными переменными любого звена являются, как правило, выходные переменные других звеньев.
Конечно, входами могут быть и внешние воздействия рассматриваемой системы, т. е независимые переменные, не являющиеся выходами каких-либо звеньев на структурной схеме таким переменным соответствуют стрелки, не исходящие ни из каких звеньев, а в графе — вершины, не имеющие входящих дуг.
В детализированной структурной схеме (ДСС) [3] используются только элементарные звенья — пропорциональные, интегрирующие и дифференцирующие, а также сумматоры. Если для всех передаточных функций системы, связывающих каждый вход с каждым выходом, выполнено условие реализуемости (степень полинома числителя не превышает степени полинома знаменателя), то система может быть описана в виде ДСС, состоящей только из безынерционных (пропорциональных и суммирующих) и интегрирующих звеньев [4]. Для этого рекомендуется пользоваться следующей методикой:
- Представить математическую модель системы
-го порядка в виде совокупности дифференциальных уравнений 1-го порядка (один из способов сделать это состоит в построении гак называемых канонических форм уравнений состояния [3D и, возможно, еще ряда алгебраических уравнений:
Здесь 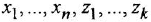
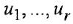
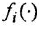
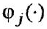
- Заменив
переменной
, переписать (1.16) в виде
Предостережение. Переходя от уравнения (1.17) к уравнению (1.18), не следует приводить подобные члены, содержащие переменную 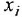
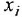
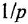
- По уравнениям (1.17), (1.18) изобразить ДСС, принимая во внимание, что уравнению (1.18) соответствует схема, показанная на рис 1.2.
Сформулированная методика сохраняет силу и при построении детализированного М-графа. Имеется, однако, тонкость: чтобы графически изобразить 
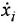
Пример №1.1.
Записать в самом общем виде уравнение, выражающее зависимость выходной величины у линейной динамической системы от входных величин 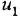
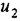
Решение:
Обозначим передаточные функции, связывающие выход с каждым из входов, как 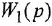
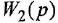
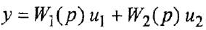
Пример №1.2.
Определить ПФ системы с одним входом 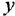
Решение:
Производя замену 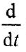
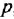
после чего переходим в комплексную область:
откуда получается искомая ПФ
Пример №1.3.
По передаточной функции
системы с одним входом и одним выходом записать ее дифференциальное уравнение.
Решение:
Обозначив выходную и входную переменные системы как 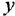
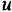
Освобождаясь от дробей и заменяя 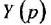
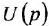
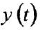
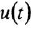
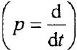
и в классической:
Пример №1.4.
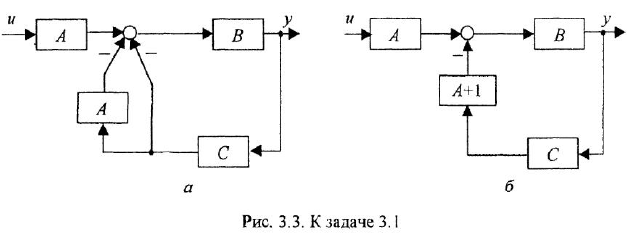
Изобразить структурную схему следящей системы по приведенным ниже уравнениям ее функциональных элементов:
где 
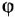
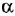
• Регулятор и усилительно-преобразовательное устройство:
где 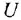
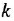
• Двигатель постоянного тока.
где 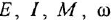
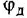
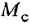
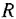
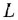
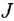
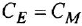
где 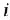
Решение:
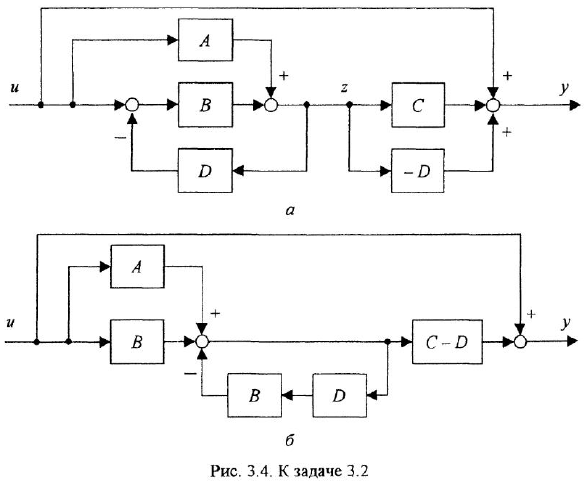
Структурная схема, построенная по уравнениям (1.19)-(1 26), показана на рис. 1.4. На ней для большей ясности рядом со звеньями написаны номера соответствующих уравнений. Последовательность изображения уравнений может быть, например, следующей: (1.19)-(1.21), (1.24), (1.23), (1.22), (1.25), (1.26).
Графическое изображение уравнений (1.20), (1.22) и (1 24) затруднений не вызывает — это пропорциональные звенья. Наличие разности в правой части уравнения (1.19) указывает на то, что необходим сумматор с двумя входами Во всех дифференциальных уравнениях заменяем 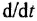
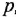
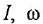
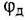
т. е им будут соответствовать интегрирующие звенья с передачей 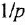
Наибольшую трудность вызывает графическая интерпретация уравнения якорной цепи двигателя (1.21). После замены 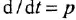
Первый из приведенных вариантов предпочтителен, поскольку в этом случае, во-первых, в структурной схеме будет на одно звено меньше, а во-вторых, последний вариант создает иллюзию того, что порядок системы на единицу выше, чем на самом деле
Замечание. Передаточную функцию
связывающую переменные 
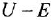
Возможно эта страница вам будет полезна:
Пример №1.5.
По уравнению (1.21) изобразить ДОС и детализированный граф.
Решение:
Перепишем (1.21) в форме уравнения (116): 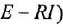
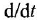
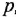
Заметим, что переменная 
Чтобы изобразить М-граф, нанесем на рисунок вершины для переменных
после чего проведем ребра с соответствующими передачами. Результат показан на рис. 1.5, б.
Полезно сравнить структурную схему и М-граф, соответствующие одному и тому же уравнению. Это, во-первых, поможет читателю в дальнейшем избежать распространенной ошибки — смешивания в одном рисунке элементов структурной схемы и графа, а во-вторых, позволит ему при необходимости легко изобразить по М-графу соответствующую структурную схему, и наоборот.
Анализ структурных схем. Передаточные функции типовых соединений звеньев САУ
Типовыми соединениями звеньев в структурных схемах являются последовательное (рис. 2.1, д), параллельное, или согласно-параллельное (рис. 2.1,6), и соединение с обратной связью, или встречно-параллельное (рис. 2.1, в). Каждое из этих соединений можно рассматривать как одно звено, считая его входной и выходной величинами, соответственно, переменные 
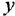
Необходимо твердо усвоить формулы для определения передаточной функции
типового соединения по передаточным функциям звеньев, образующих это соединение:
(Если какая-либо из переменных 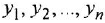
• Соединение с обратной связью:
В последней формуле необходимо выбирать знак «плюс» в случае отрицательной обратной связи и «минус» — в случае положительной. Отметим, что в этой формуле выражение 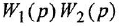
Если структурная схема содержит только типовые соединения, то, как бы сложна ни была эта схема, по ней всегда можно определить передаточную функцию, связывающую заданные переменные, путем последовательного применения формул (2.1)-(2.3). Если же, кроме типовых, есть соединения с более сложной топологией (подробнее об этом см. в 3 1), то необходимо либо использовать теорему Мейсона, рассматриваемую в 2.2, либо применить метод эквивалентных структурных преобразований, излагаемый в 3.1
Теорема Мейсона (Мэзона)
Теорема Мейсона позволяет определить передаточную функцию, связывающую любые две переменные структурной схемы или М-графа. Поскольку первоначально теорема была сформулирована для графов, а затем распространена на структурные схемы, уточним некоторые топологические термины, знание которых необходимо для правильного применения этой теоремы.
Маршрутом в теории графов называют последовательность ребер, в которой соседние ребра инцидентны одной и той же вершине (напомним, что вершина 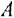
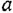
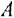
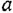
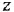
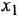
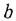
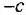
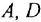
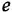
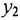
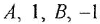
Путь — это маршрут без повторяющихся ребер и вершин На рис. 2.2, б последовательность ребер с передачами 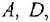
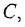
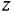
Передачей пути называется произведение передач всех звеньев (в графе — ребер), образующих этот путь, причем необходимо учитывать и знаки, с ко-
торыми переменные данного пути входят в сумматоры, встречающиеся на этом пути. Па рис 2.2, а, б путь между переменными 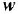
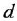
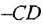
Контуром как в графе, так и в структурной схеме называют замкнутый путь. Для графа это означает, что начальная и конечная вершины пути совпадают.
Передача контура — это произведение передач всех звеньев (или ребер), образующих контур, с учетом знаков в сумматорах Например, контур в графе на рис. 1.5, б имеет передачу 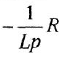
Говорят, что контур не касается другого контура или пути, если он не имеет с ним общих переменных. На рис 2.2, а, б контур с передачей 
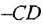
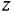
Согласно теореме Мейсона, передача, связывающая некоторую «входную» переменную 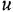
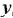
Обозначения, использованные в формулах (2.4)-(2.6), имеют следующий смысл: 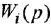
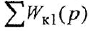
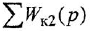
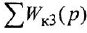
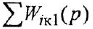
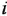
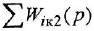
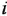
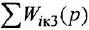
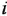
Заметим, что два пути или два контура могут частично совпадать; тем не менее, если они различаются хотя бы одним звеном (ребром), то это рахпич-ные пути или контуры.
Решение любой задачи, требующей применения теоремы Мейсона, следует начинать с анализа структурной схемы или М-графа. Если схема сложна, то рекомендуется сначала выписать передачи всех путей, связывающих заданные переменные, и передачи всех контуров, отметив специально «некасающиеся» контуры После этого можно непосредственно записывать искомую передаточную функцию в соответствии с формулами (2 4)-(2.6).
Хотя при определении передаточных функций по теореме Мейсона в качестве входной переменной практически всегда выступает какое-либо внешнее воздействие, ничто не мешает применять эту теорему в ситуации, когда входом является некоторая «внутренняя» переменная структурной схемы. В этом случае надо лишь «усечь» схему, исключив из нее все пути, направленные к указанной входной переменной от заданного выхода и от внешних входных воздействий.
Удобство теоремы Мейсона заключается в возможности быстро записать требуемую передаточную функцию без многократного перерисовывания структурной схемы, что часто бывает необходимо в случае применения альтернативного метода структурных преобразований (см. 3.1) Вместе с тем, с ростом сложности схемы резко возрастает опасность «пропустить» при ее анализе какой-нибудь путь или контур либо не заметить факта «некасания» Поэтому в целом метод структурных преобразований считается более надежным способом определения передаточной функции по структурной схеме
Анализ установившегося режима по структурной схеме при постоянных входных воздействиях
Для исследования динамических систем, в том числе на ЭВМ, бывает важно уметь анализировать установившийся режим при постоянных внешних воздействиях Это можно делать различными способами — например, с помощью алгебраических методов пространства состояний. Здесь мы рассмотрим простой способ, позволяющий определить установившиеся значения всех переменных системы по структурной схеме.
Пусть система асимптотически устойчива (изложение методов анализа устойчивости выходит за рамки данного учебного пособия) Тогда, если все входные (внешние) воздействия постоянны, то с течением времени (теоретически — при 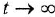
- Если схема содержит интегрирующее звено, описываемое, как известно, уравнением
, то из
(индекс
служит обозначением установившегося режима) следует, что
. Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.
2 Если в схеме имеется дифференцирующее звено, описываемое уравнением 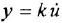
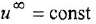
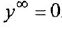
Большинство звеньев структурной схемы — это позиционные звенья, описываемые передаточными функциями (1.5), (I 10), (1 12) и (I 13), причем в трех последних в общем случае присутствует коэффициент передачи 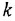
Коэффициент передачи к звена (системы) может быть определен двояко:
а) 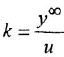
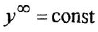
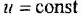
б) 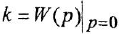
Последнее выражение — это одновременно и практический способ определения коэффициента передачи.
Общим свойством позиционных звеньев является то, что при подаче на вход такого звена постоянной величины на его выходе с течением времени также устанавливается постоянное значение. ПФ позиционного звена в установившемся режиме вырождается в коэффициент передачи 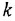
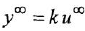
Консервативное звено с ПФ (1.14) также относится к позиционным, но, в отличие от остальных, не является асимптотически устойчивым. При наличии в схеме консервативного звена (или эквивалентного ему встречно-параллельного соединения интегрирующего звена 2-го порядка и пропорционального звена) в системе в установившемся режиме будут наблюдаться незатухающие колебания, т. е. по крайней мере некоторые переменные будут изменяться по гармоническому закону. Анализ такого установившегося режима выходит за рамки излагаемого здесь метода.
В заключение отметим, что отводы по переменным, установившиеся значения которых равны нулю, при анализе установившегося режима можно не учитывать.
Возможно эта страница вам будет полезна:
Пример №2.1.
По структурной схеме (рис 2.3, а) определить передаточные функции 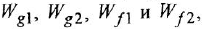
Решение:
Сначала найдем ПФ 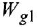
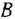
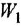
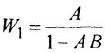
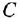
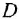
согласно-параллельное соединение; в соответствии с формулой (2.2) его 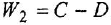
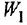
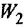
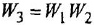
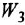
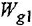
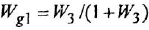
Для сравнения получим искомую ПФ иначе — с помощью теоремы Мейсона. От 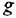
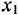
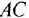
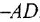
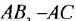
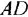
что, разумеется, совпадает с ранее полученным выражением.
Чтобы найти ПФ 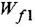
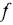
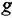
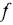
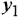
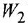
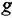
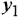
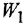
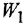
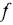
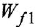
До сих пор на структурных схемах выходная величина всегда изображалась стрелкой, заканчивающей горизонтальную цепочку звеньев, берущую начало от места приложения задающего воздействия. Если же в качестве выхода рассматривается какая-либо «внутренняя» переменная (в данной задаче — 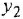
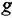
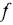
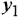
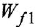
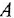
на рис. 2.3, в прямая связь имеет передачу — 
С учетом сказанного, легко записать искомые ПФ
Обращаем внимание читателя на то, что все четыре найденные передаточные функции имеют, как это всегда и должно быть, одинаковые знаменатели.
Чтобы найти ПФ 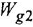
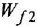
Пример №2.2.
С помощью теоремы Мейсона по структурной схеме или М-графу, изображенным на рис. 2.2, а и б, определить передаточные функции 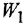
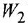
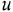
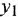
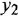
Решение:
Определим ПФ 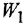
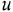
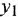
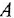
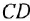
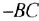
При нахождении 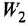
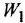
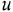
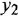
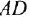
Пример №2.3.
С помощью теоремы Мейсона определить передачу между переменными 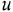
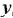
Решение:
В схеме только один контур, но четыре пути: с передачами, соответственно, 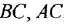
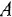
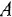
Возможно эта страница вам будет полезна:
Преобразование структурных схем. Эквивалентные структурные преобразования
Если в структурной схеме имеются не только типовые соединения звеньев (см. 2.1), но и другие, более сложные, то при необходимости определить передаточную функцию, связывающую заданные переменные, можно поступить различным образом: воспользоваться теоремой Мейсона (о ее достоинствах и недостатках было сказано ранее) либо применить метод эквивалентных преобразований структурных схем (короче — метод структурных преобразований), излагаемый далее. Этот метод, как показывает практика преподавания, не так легок для начального освоения, как теорема Мейсона, и даже может показаться громоздким, но в действительности после приобретения необходимых навыков становится удобным, эффективным и надежным инструментом анализа систем. Знание этого метода обязательно для специалиста в области автоматического управления. Рассмотрим сущность метода эквивалентных структурных преобразований.
Обычно в схеме можно выделить две части, не обязательно компактные одна состоит только из типовых соединений, к которым, следовательно, сразу могут быть применены формулы (2 1)—(2.3) для определения передаточных функций, другая же — назовем ее преобразуемой частью — содержит различного рода нетиповые соединения звеньев. В чем особенность таких соединений, и почему они являются предметом специального рассмотрения0
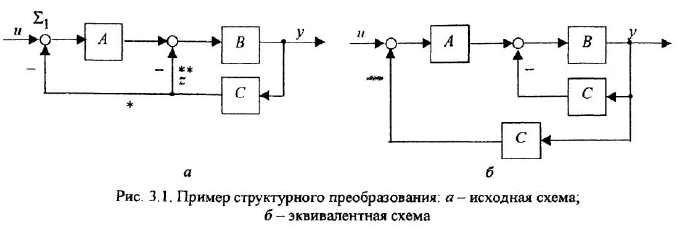
На рис 3.1, а показана структурная схема, в которой вообще нет типовых соединений. Если бы в этой схеме отсутствоват отвод «*» (конечно, вместе с сумматором 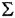
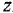
Возникает вопрос: нельзя ли заменить эту схему другой так, чтобы ее передаточная функция не изменилась, но отвод «*» шел не с выхода звена с передачей 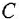
соединения, а передаточная функция, связывающая переменные 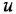
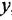
Приведение схемы к типовому виду осуществляется выполнением некоторого количества операций преобразования. После выполнения любой из этих операций новая схема должна в определенном смысле быть эквивалентна предыдущей Пусть та часть (фрагмент) структурной схемы, над которой совершается операция преобразования, имеет 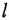
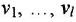
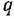

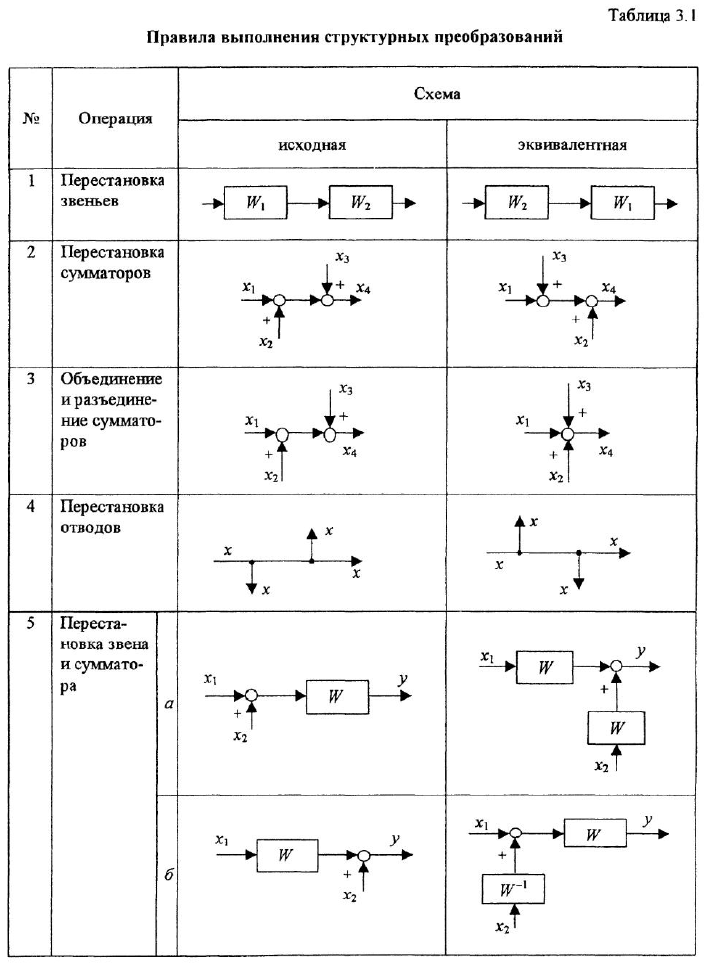
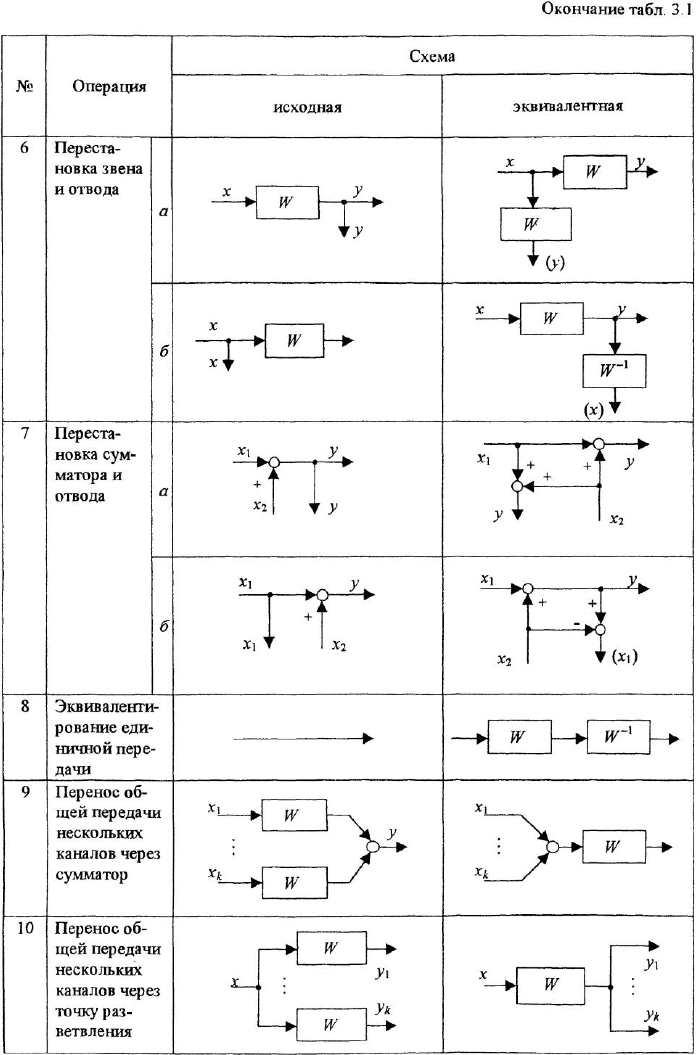
связывающих каждый вход 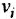
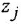
В табл. 3.1 приведены правила, по которым выполняются структурные преобразования. Подавляющее большинство приведенных здесь операций -это различного рода перестановки: звеньев, сумматоров и отводов. Для пояснения каждой операции в соответствующей горизонтальной графе показаны две схемы: исходная и эквивалентная ей преобразованная Однако как раз в силу эквивалентности всех преобразований каждую пару схем можно просматривать и в обратном порядке, считая эквивалентную схему исходной Например, операция 3 носит двойственный характер: сумматоры можно объединять и, наоборот, разделять.
При начальном изучении табл. 3.1 полезно убедиться в корректности каждой операции. Для этого рекомендуется проверить совпадение передаточных функций, связывающих каждый вход с каждым выходом в исходной
и эквивалентной схемах. Чтобы получить требуемую ПФ, необходимо просто «пройти» вдоль пути, связывающего данный вход с данным выходом, перемножая передачи всех звеньев этого пути и учитывая знаки в сумматорах. Можно поступить и иначе, в обеих схемах для каждой выходной переменной записать уравнение, описывающее зависимость этой переменной от всех входных переменных, после чего сравнить эти уравнения.
Особо подчеркнем следующее обстоятельство: приведенные в табл 3.1 правила выполнения операций не предназначены для запоминания. Необходимо просто понять логику построения эквивалентной схемы по имеющейся исходной и всякий раз при решении конкретной задачи поступать аналогично.
Рассмотрим теперь правила выполнения отдельных операций Все множество приведенных в табл. 3.1 операций можно условно разделить на три группы Первую из них составляют простейшие операции 1-4, которые вряд ли нуждаются в пояснениях.
Группу основных операций составляют операции 5-7. Именно они являются главным инструментом преобразования структурных схем. Рассмотрим перестановку звена и сумматора — например, в случае, когда сумматор стоит перед звеном (в табл. 3.1 — операция 5, вариант а). Если просто поменять местами сумматор и звено с передачей 
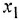

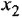

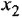

Аналогично рассуждаем при обосновании правила перестановки звена и отвода. Рассмотрим операцию 6, вариант а. Просто поменять местами звено и отвод нельзя: в этом случае отвод будет по переменной 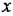
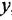
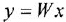

Перестановка сумматора и отвода — наиболее сложная из операций преобразования структурных схем, и ее по возможности следует избегать. Здесь тоже есть два варианта взаимного расположения переставляемых элементов (варианты а и б операции 7 в табл. 3.1) В связи с этим следует со всей определенностью сказать, что объективная необходимость в выполнении перестановки по варианту б встречается крайне редко Бели при анализе конкретной схемы выясняется, что без перестановки сумматора и отвода обойтись нельзя, то необходимо, прежде всего, искать возможность выполнить перестановку по варианту а, такая возможность, скорее всего, существует.
Обращаем внимание на то, что, согласно правилу выполнения данной операции, в эквивалентной схеме вместо отвода по переменной 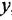
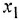
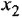
Однако, оказывается, перестановку сумматора и отвода можно выполнить гораздо более простым способом, исключающим появление дополнительного сумматора, а значит, и не требующим последующих операций по упрощению схемы. Суть этого способа (отразить его в табл. 3.1 не представляется возможным) состоит в следующем. В исходной системе отвод по переменной у, или в данном случае удобнее сказать — сама переменная 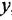

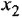

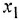
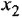

Последнюю группу в табл. 3.1 составляют операции 8-10, которые можно назвать вспомогательными. Справедливость операций 8^и 10 очевидна, при этом заметим, что величины 
В чем польза трех последних операций? Рассмотрим более внимательно операцию 9. Ее смысл заключается в возможности выноса общей передачи из нескольких суммирующихся каналов (имеются в виду линии, входящие в сумматор) в канон за сумматором. Очевидно, что это упрощает схему, особенно если число входящих в сумматор каналов велико. Однако, возможно, еще большая польза этой операции состоит в другом. Если, наоборот, эквивалентную схему принять за исходную, то операция 9 трактуется по-другому: передачу звена, расположенного за сумматором, можно поместить в каждый из суммирующихся каналов Это позволяет иначе взглятть на уже рассмотренную операцию 5 перестановки звена и сумматора (в варианте а). Очевидно, что она полностью совпадает с операцией 9, и, следовательно, если в схеме последовательно расположены сумматор и звено, то операцию 5 над ними можно трактовать уже не как взаимную перестановку, а как «ввод» звена в каждый из каналов — это правило легко запоминается учащимися
Аналогично обстоит дело с операцией 10. Если рассматривать приведенную в табл 3.1 пару схем слева направо, то правило звучит так: общую передачу всех связей, отходящих от точки разветвления, можно внести в связь перед этой точкой. Рассматривая эти же схемы в обратном порядке, можно прийти к следующему выводу: передачу звена, стоящего до точки разветвления, можно внести во все отходящие от этой точки связи. Знание этого правила позволяет, не задумываясь, выполнять операцию 6 перестановки звена и отвода (вариант а).
Операция 8 удобна тем, что позволяет искусственно создать в какой-либо связи звено с требуемой передачей — чтобы получить возможность вынести эту передачу из двух или более связей, т. е. выполнить операцию 9 или 10.
В заключение укажем на еще одно правило, которое бывает полезно при упрощении схем и выполнении других процедур их преобразования к заданному виду: уравнения, описывающие систему, не изменятся, если в структурной схеме у всех переменных, связанных с каким-либо сумматором, изменить знак на противоположный. Другими словами, можно изменить знаки у всех стрелок, входящих в сумматор, и поставить звено с передачей -1 в связь, выходящую из сумматора. Эта операция, по существу, является частным случаем операции 9 при 
Знание правил структурных преобразований не дает, однако, ответа на вопрос, в каком порядке следует преобразовывать схему к типовому виду при решении конкретной задачи. Ответить определенно на него невозможно, поскольку задачи такого типа решаются, как правило, не единственным образом То, какие именно операции и в какой последовательности будут использованы, зависит как от многообразия вариантов решения, так и от опыта и, не в последнюю очередь, от личных предпочтений специалиста, выполняющего структурные преобразования. Нет нужды доказывать, что при наличии нескольких возможных алгоритмов решения задачи необходимо выбирать наиболее простой.
Несмотря на сказанное, некоторые общие рекомендации относительно алгоритма преобразования структурных схем все же можно дать. Прежде всего, необходимо каждое имеющееся в схеме типовое соединение звеньев заменить эквивалентным звеном, снабдив его обозначением соответствующей передаточной функции. Затем целесообразно выполнить операции перестановки звена и отвода или/и звена и сумматора (как уже указывалось, операцию перестановки сумматора и отвода без необходимости применять не следует), чтобы в результате образовались новые типовые соединения. Их нужно опять заменить эквивалентными звеньями и т. д. Рекомендуется после каждого этапа преобразований перерисовывать схему с новыми обозначениями.
Возможно эта страница вам будет полезна:
Операция инверсии
Полезным видом структурно-топологических преобразований является операция инверсии. Ее применяют
- а) для приведения структурной схемы к виду, удобному для цифрового и аналогового моделирования, путем устранения дифференцирующих звеньев,
- б) при анализе установившихся режимов для устранения некорректности типа деления на ноль (в передаточных функциях вида \/р при р-> 0),
- в) для получения из схемы общего вида некоторых частных структурных схем путем предельного перехода при стремлении какого-либо параметра к бесконечности или к нулю.
Различают инверсию пути и контура. Главной чертой этих операций является изменение направления пути (контура) на противоположное
Рассмотрим операцию инверсии пути. Чтобы излагаемое далее правило было более понятно, проиллюстрируем его примером. Пусть требуется про-инвертировать путь между переменными 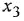
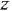
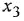
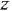
Для рассматриваемого примера результат инверсии показан па рис 3.2, а. Сравнение этой схемы с исходной позволяет лучше усвоить излагаемое далее правило инверсии пути.
Чтобы проинвертировать некоторый путь между двумя переменными структурной схемы, необходимо изменить:
1) направление пути на противоположное;
2) передачи всех звеньев этого пути — на обратные;
3) знаки всех воздействий, подходящих к данному пути, — на противоположные.
Это правило можно рассматривать как алгоритм выполнения данной операции. На первом этапе следует перерисовать схему, изменив направления всех стрелок рассматриваемого пути (и только его!) и пока воздержавшись от записи передач внутри графических изображений звеньев. Далее необходимо записать эти передачи как обратные исходным, причем, если на инвертируемом пути встречаются сумматор и принадлежащая этому же пути стрелка, входящая в сумматор со знаком «минус», то последний следует интерпретировать как звено с передачей -1. В заключение меняют на противоположные знаки, с которыми к рассматриваемому пути подходят (в сумматорах) внешние воздействия, в том числе воздействия от остальной части схемы.
Заметим, что с математической точки зрения инверсия пути соответствует разрешению алгебраического уравнения, описывающего данный путь, относительно новой переменной.
Так, в рассмотренном примере исходной и преобразованной схемам соответствуют следующие два варианта одного и того же уравнения:
Инверсия контура в практическом плане является наиболее важной из двух рассматриваемых здесь операций. Именно она является инструментом решения задач, перечисленных в начале раздела.
Чтобы проинвертировать некоторый контур структурной схемы, необходимо:
1) любой сумматор этого контура принять за опорный (обозначим его 
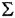
2) направление контура изменить на противоположное; в результате этого прямая связь становится обратной, а обратная — прямой;
3) передачи всех звеньев контура изменить на обратные (как-уже пояснялось, знаки «минус» при входящих в сумматоры стрелках данного контура тоже необходимо рассматривать как звенья этого контура, имеющие передачу -1);
4) знаки прямой и обратной связей изменить на противоположные, вставив звено с передачей -1 непосредственно у опорного сумматора;
5) знаки всех воздействий, подходящих к данному контуру извне, за исключением воздействий, приложенных к опорному сумматору, заменить на противоположные.
Применение этого правила проиллюстрируем на примере контура, изображенного на рис. 3.2, б Рассмотрим два варианта назначения опорного сумматора (приводящие, таким образом, к двум вариантам решения) — они обозначены на схеме как 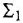
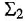
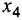
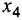
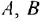

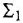
Пусть опорным является сумматор 
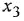
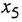
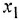
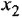
Теперь рассмотрим вариант с опорным сумматором 
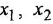
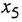
Хотя выбор различных опорных сумматоров привел к различным структурным схемам, эти схемы легко получаются одна из другой изменением знаков всех переменных в сумматорах 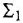
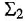
Если требуется привести структурную схему к виду, удобному для моделирования, путем устранения имеющихся в ней дифференцирующих звеньев, то эту задачу можно решить с помощью операции инверсии контура в том случае, если инвертируемый контур не содержит интегрирующих звеньев. В противном случае при замене передач звеньев кон тура на обратные интегрирующие звенья превратятся в дифференцирующие. В такой ситуации делу могут помочь структурные преобразования, а в сложных случаях — применение методов пространства состояний (канонических форм, которые всегда приводят к структурным схемам без дифференциаторов [3]).
Пример №3.1.
По структурной схеме, изображенной на рис 3.1, а, определить передаточную функцию, связывающую переменные 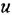
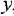

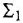
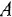
Решение:
На рис. 3.1,6 показан результат решения задачи первым способом. Чтобы получить его, необходимо сначала перерисовать без каких-либо изменений ту часть схемы, которая не подвергается операции преобразования. В данном случае это вся схема за исключением отвода «». Специально обращаем внимание на то, что звено с передачей 
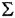
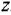
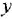
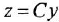


Для решения вторым способом удобно воспользоваться операцией 9 (см. табл. 3.1): убрав звено с передачей 


Пример №3.2.
По схеме, изображенной на рис. 2.2, г, определить передаточную функцию от и к у методом структурных преобразований
Решение:
Данная схема является примером случая, когда нельзя обойтись без операции перестановки сумматора и отвода Наиболее быстро задача решается взаимной перестановкой первого (слева) сумматора и отвода по переменной 
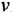
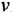
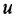
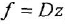
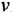
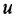
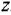
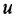
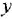
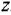
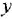
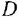
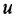
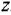
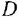

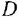

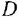
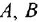
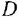
между переменными 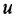
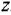
Это выражение после упрощения совпадает с найденным в задаче 2.3
Пример №3.3.
По структурным схемам, приведенным на рис. 2.2, а и в, определить методом структурных преобразований передаточные функции 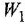
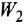
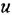
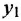
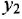
Решение:
Главную трудность при нахождении ПФ 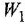
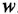
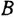
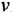
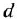
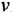
Одновременно сделаем перестановку крайнего левого сумматора и звена с передачей 
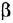

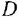
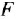

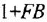
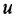
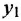
что после подстановки выражения для 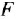
Преобразования схемы на рис. 2.2, в, необходимые для нахождения ПФ 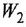


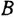
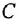
что совпадает с ПФ в задаче 2.2.
Пример №3.4.
Выполнить инверсию контура 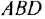
Решение:
Примем левый сумматор за опорный, а переменную 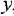
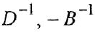
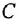
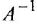
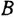

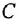
Полезно убедиться, что передаточная функция системы после инверсии не изменилась.
Пример №3.5.
В структурной схеме, изображенной на рис. 2.1, в, с помощью эквивалентных структурных преобразований сделать обратную связь единичной.
Решение:
Задача предназначена для самостоятельного решения Рекомендуется использовать операции 8 и 10 из табл. 3.1.
Пример №3.6.
На рис. 3.7, а показана упрошенная структурная схема системы автоматического регулирования скорости электродвигателя постоянного тока, соединенного с рабочим механизмом упругой механической связью, имеющей жесткость с. Требуется с помощью операции инверсии контура: а) получить частную схему для случая жесткой связи двигателя с механизмом 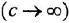
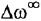
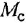
Пояснение Кроме названных, в схеме имеются следующие переменные: 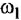
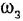
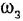
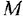
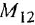
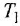
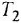
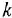
Решение:
Проинвертируем контур, содержащий звенья с передачами 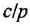
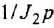
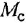
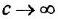
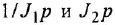
тельной обратной связью, передача которого есть 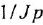
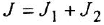
Чтобы решить вторую часть задачи, выполним инверсию полученного контура (ввиду простоты эту операцию не поясняем). Для перехода к схеме установившегося режима достаточно заменить обозначения переменных на установившиеся значения и принять 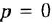
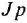
Пример №3.7.
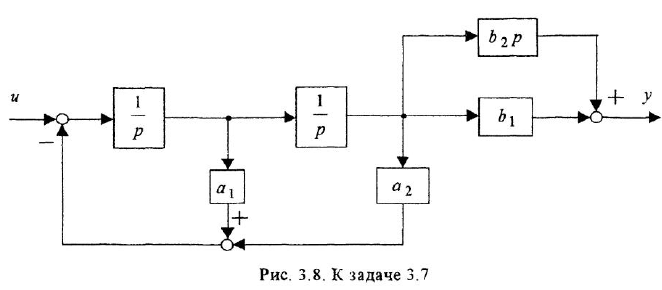
Структурную схему, изображенную на рис. 3.8, привести к виду, удобному для моделирования, устранив дифференцирующее звено.
Решение:
Задача решается путем переноса отвода, идущего на вход звена с передачей 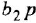
Построение и анализ логарифмических частотных характеристик. Логарифмические частотные характеристики
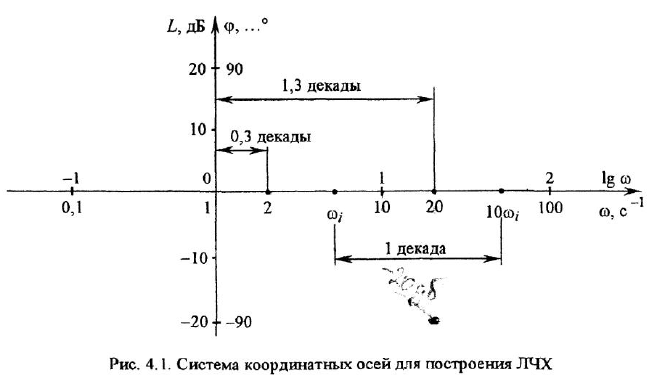
Математический аппарат частотных характеристик, в особенности — логарифмических частотных характеристик, является весьма эффективным инструментом анализа и синтеза автоматических систем, даже несмотря на наличие мощных методов так называемой «современной теории управления» (методов пространства состояний, вход-выходного подхода и др.) и огромные возможности вычислительной техники. Частотные характеристики благодаря сочетанию строгости, простоты, наглядности и информативности не только являются удобным средством в руках инженера и исследователя, но и, после приобретения достаточного опыта, вырабатывают у специалиста интуицию, необходимую для приближенной оценки динамических свойств систем и поиска методов их улучшения.
Как известно, частотная передаточная функция (ЧПФ) 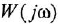
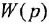
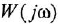
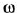
называются, соответственно, амплитудной (АЧХ) и фазовой (ФЧХ) частотными характеристиками. Если же ЧПФ представлена в алгебраической форме
называются, соответственно, вещественной (ВЧХ) и мнимой (МЧХ) частотными характеристиками.
Чтобы построить АФХ, необходимо
1) записать аналитические выражения для 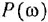
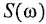
2) задавая некоторые характерные значения 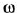
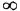
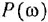
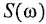
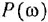
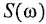
3) задав на комплексной плоскости систему координатных осей 
называется логарифмической амплитудной частотной характеристикой (ЛAX) и графически изображается как функция частоты 
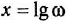
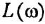
Любой интервал частот 
На рис. 4.1 изображена система координат, которой пользуются при построении ЛЧХ. На ней показан пример оцифровки осей, причем для оси абсцисс даны два варианта оцифровки, используемые в литературе: снизу от оси — для 

Необходимо уметь правильно отмечать на оси абсцисс точки, соответствующие конкретным значениям частоты. Пусть, например, требуется нанести на ось частот две точки: 2 


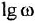




Также необходимо уметь строить в принятом масштабе наклонные участки асимптотических ЛАХ, т е. отрезки прямых, имеющих стандартные коэффициенты наклона Например, чтобы через данную точку провести прямую, имеющую коэффициент наклона -20 дБ/дек, следует найти вторую точку, отстоящую от заданной на 1 декаду вправо и на 20 дБ вниз (либо, наоборот, на 1 декаду влево и на 20 дБ вверх), после чего соединить обе точки отрезком прямой. Коэффициенты наклона 0, ±20 дБ/дек, ±40 дБ/дек… сокращенно обозначают 0, ±1, ±2 . ..
При изучении теории автоматического управления обязательным является знание логарифмических частотных характеристик типовых звеньев САУ, перечисленных в 1.1. Этот материал можно найти в любом учебнике по теории автоматического управления Здесь мы, не приводя графиков ЛЧХ типовых звеньев, отметим их существенные особенности, знание которых облегчает усвоение этого материала.
Общей чертой трех типов звеньев — пропориионального с ПФ (1 5), интегрирующего и дифференцирующего (произвольного порядка), описываемых передаточными функциями (1.7) и (1.9), — является то, что для них как ЛАХ, так и ЛФХ представляют собой прямые При этом ЛАХ пропорционального звена — горизонтальная прямая с ординатой 20 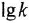
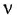
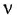
Каждая из этих точек соответствует своей, одной из двух форм записи передаточных функций (1.7) и (1.9) — с использованием коэффициента 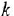
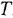
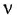
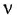
С остальными из перечисленных в 1.1 типовых звеньев дело обстоит сложнее. Для каждого из них различают два вида ЛАХ — точную, описываемую выражением (4.1), и асимптотическую. При компьютерном моделировании САУ с помощью специализированных математических пакетов, например Control System Toolbox системы Matlab, мы имеем возможность рассчитывать и видеть на экране график именно точной ЛАХ исследуемой системы. Однако в практике предварительного инженерного анализа систем и оценки вариантов закона управления обычно имеют дело с асимптотическими ЛАХ, широкое применение которых объясняется простотой их построения даже для весьма сложных систем и богатством заключенной в них информации.
Асимптотическая логарифмическая амплитудная частотная характеристика — это ломаная, отрезки которой являются асимптотами для точной ЛАХ. Для звеньев, описываемых передаточными функциями (1.10), (1.11), (1 13) и (1 14) (апериодическое звено 2-го порядка мы исключаем из рассмотрения, поскольку оно заменяется последовательным соединением двух апериодических звеньев 1-го порядка), асимптотическая ЛАХ состоит из двух асимптот: низкочастотной (к ней точная ЛАХ приближается при 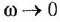
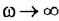
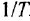
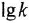
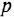
Фазовые характеристики трех звеньев графически представляют собой плавные кривые; они являются следующими функциями частоты: 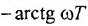
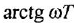
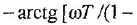
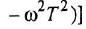
Заметам, что передаточные функции (1 10) и (1.11) апериодического и форсирующего звеньев являются взаимно обратными. Как следствие, их ЛЧХ симметричны друг другу относительно оси частот. То же самое можно сказать об ЛЧХ дифференцирующего и интегрирующего звеньев. В связи с этим набор «типовых» передаточных функций можно расширить, введя в него функции, обратные передаточным функциям (1 13) и (1 14) колебательного и консервативного звеньев. Соответственно, ЛЧХ таких звеньев будут зеркальным отображением ЛЧХ указанных звеньев. Такой расширенный набор позволяет почти любую передаточную функцию, не являющуюся типовой, представить в виде произведения типовых передаточных функций
В процессе анализа САУ часто возникает необходимость в построении ЛЧХ систем с довольно сложной структурой Будем предполагать, что структурная схема системы уже преобразована так, что содержит только типовые соединения Следовательно, возникает задача построения ЛЧХ типовых соединений звеньев по известным ЛЧХ самих этих звеньев
Рассмотрим последовательное соединение Основной результат состоит в том, что как ЛАХ, так и ЛФХ последовательного соединения звеньев могут быть получены суммированием соответствующих характеристик звеньев, образующих это соединение (уточним, что нас интересует, главным образом, графическое сложение частотных характеристик). Это позволяет сравнительно легко строить ЛЧХ длинных цепочек звеньев
На данный результат можно посмотреть и с другой стороны. Среди звеньев структурной схемы могут оказаться и такие, передаточные функции которых не совпадают ни с одной из рассмотренных ранее передаточных функций типовых звеньев. Однако в большинстве случаев такая «сложная» передаточная функция всегда может быть представлена в виде произведения типовых передаточных функций, а значит, ее можно рассматривать как ПФ последовательного соединения типовых звеньев, что позволяет строить ЛЧХ по такой ПФ суммированием «типовых» составляющих.
Несмотря на ясность изложенного подхода, необходимо сделать существенную оговорку. Основные преимущества метода ЛЧХ связаны, в первую очередь, с простотой ручного построения асимптотических ЛАХ типовых звеньев САУ и, как следствие, систем в целом (мы говорим именно о ручном построении как основе предварительных, прикидочных расчетов автоматических систем; впрочем, очень часто расчеты, выполненные с помощью ЛЧХ, являются весьма точными). В отличие от асимптотических ЛАХ, которые можно строить вполне точно с соблюдением необходимых масштабов, фазовые характеристики большинства даже типовых звеньев и тем более их последовательных соединений могут быть построены вручную только эскизно, поскольку описываются не очень простыми выражениями. Если бы оказалось, что для анализа каких-либо свойств системы необходимо точное построение ее ЛФХ, то это свело бы на нет преимущества использования аппарата асимптотических ЛАХ. К счастью, большинство систем, с которыми приходится иметь дело, относятся к так называемым минимально-фазовым системам, для которых существует однозначная связь между амплитудной и фазовой частотными характеристиками и, следовательно, можно обойтись построением только ЛАХ — если, конечно, имеется возможность на любом этапе расчета восстановить (в случае необходимости) ЛФХ по имеющейся ЛАХ или хотя бы оценить значение фазы в любой точке ЛАХ (подробно об этом говорится в 4 2).
Таким образом, наибольшее значение для практики анапиза и синтеза автоматических систем имеет построение асимптотических ЛАХ типовых соединений звеньев. Для последовательного соединения или, что равнозначно, для передаточной функции сложного вида результирующая ЛАХ может быть найдена, как уже было сказано, простым суммированием составляющих, соответствующих передаточным функциям отдельных звеньев или сомножителям сложной передаточной функции. Однако на практике этот способ применяется редко. Более эффективной является специальная методика, позволяющая строить результирующую ЛАХ по передаточной функции сложного вида без предварительного изображения отдельных составляющих. Методика базируется том факте, что ЛАХ пропорционального, интегрирующего и дифференцирующего звеньев являются бесконечными прямыми и, следовательно, вносят свой вклад в результирующую ЛАХ во всем диапазоне частот, в то время как влияние асимптотических ЛАХ звеньев других типов начинается только с соответствующей частоты сопряжения (если рассматривать весь частотный диапазон слева направо), поскольку их низкочастотные асимптоты, если полагать коэффициент передачи этих звеньев равным единице, совпадают с осью абсцисс.
Пусть передаточная функция имеет следующий вид (или приведена к таковому):
где функция 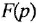
a 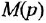
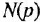
http://nauka.club/khimiya/khimicheskie-uravneniya.html
http://lfirmal.com/primery-resheniya-zadach-po-tau/


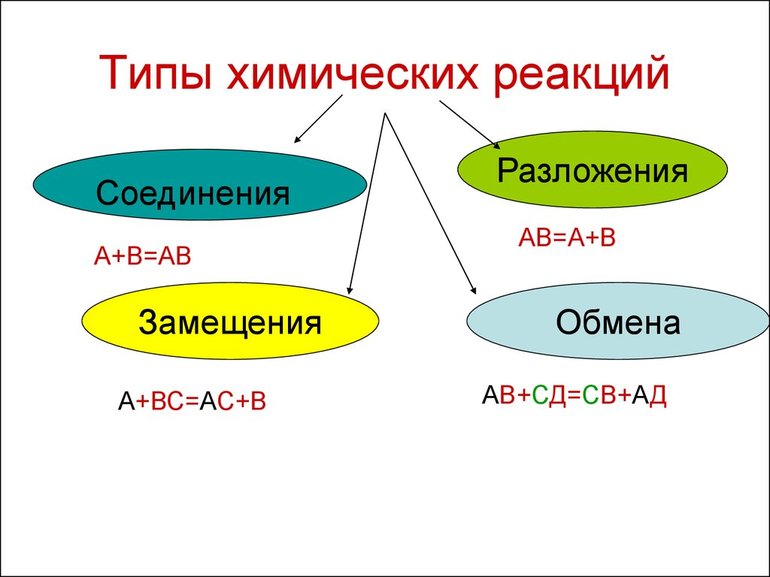

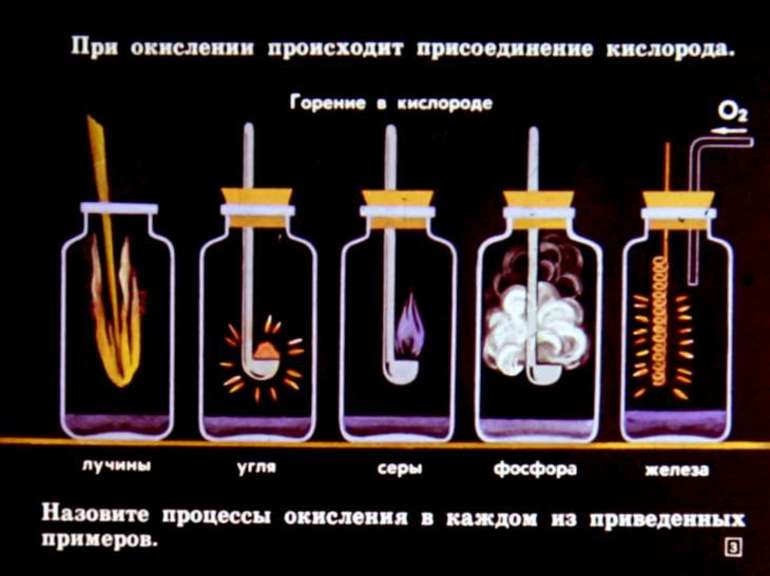
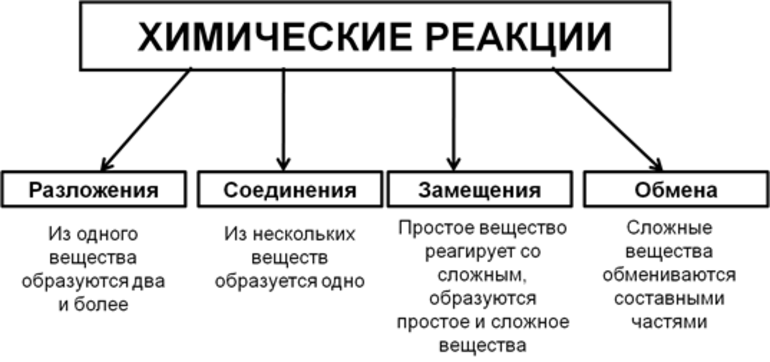
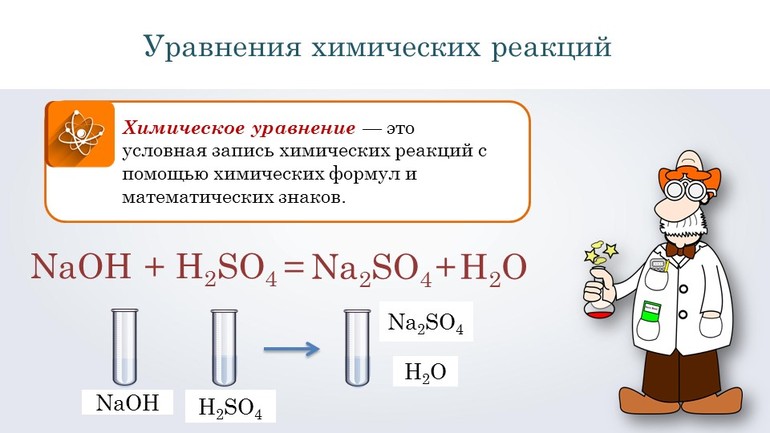



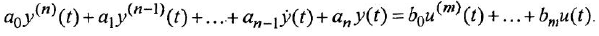
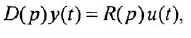
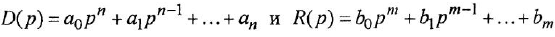
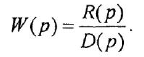
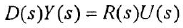
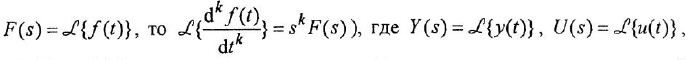
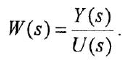
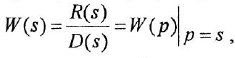
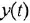 и
и 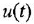 на
на 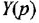 и
и 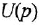 .
.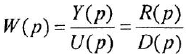 .
.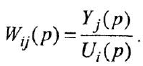
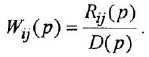
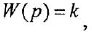
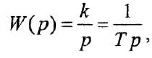
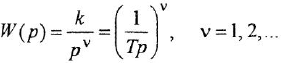
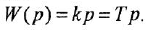
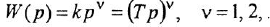
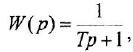
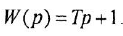
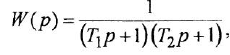
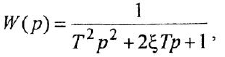
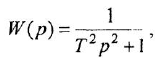
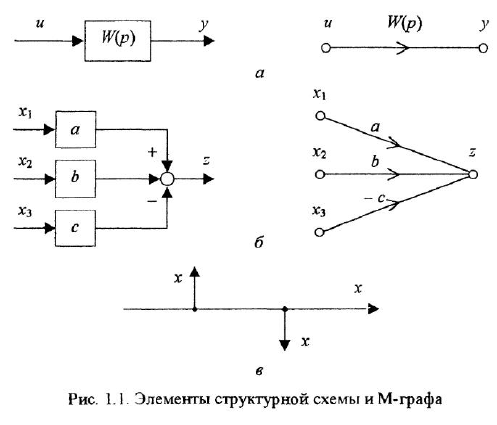
 -го звена) выразить выходную переменную
-го звена) выразить выходную переменную  (
(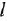 — число входов):
— число входов):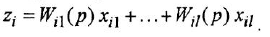
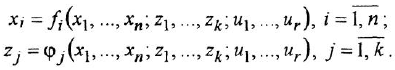
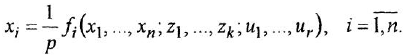
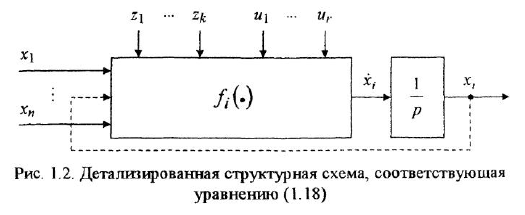
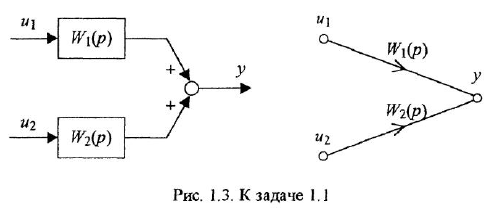
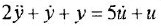
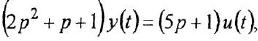
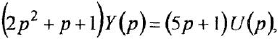
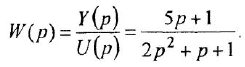
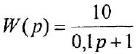
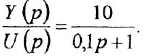
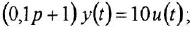
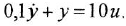
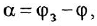
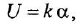
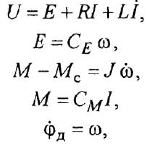
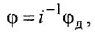
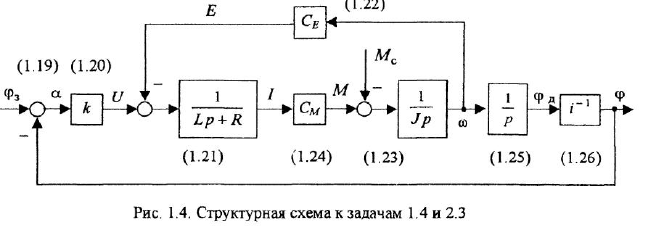
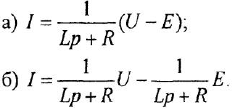
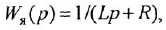
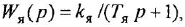
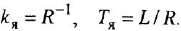
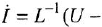
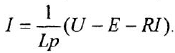
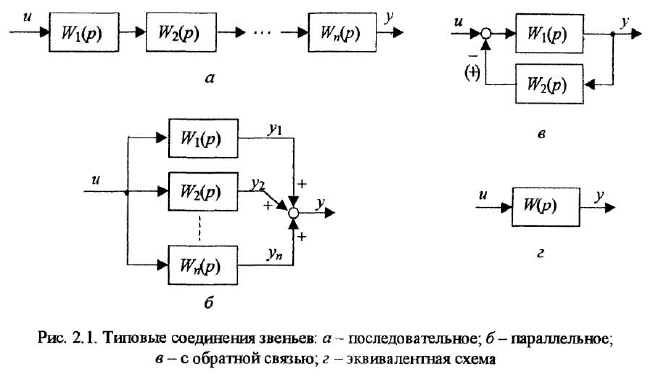
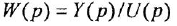
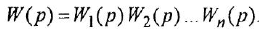
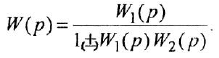
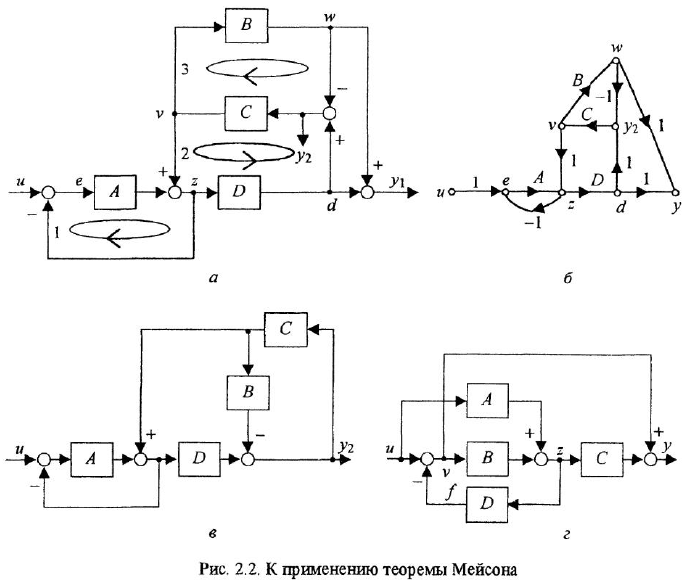
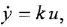 , то из
, то из 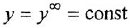 (индекс
(индекс 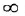 служит обозначением установившегося режима) следует, что
служит обозначением установившегося режима) следует, что 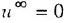 . Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.
. Таким образом, в асимптотически устойчивой системе с постоянными внешними воздействиями входные переменные всех интегрирующих звеньев в установитиемся режиме равны нулю.