Как записывается уравнение неразрывности для потока

Уравнение неразрывности и уравнение Бернулли.

Уравнение неразрывности потока и уравнения Бернулли являются основными уравнениями гидродинамики. При изучении потоков жидкости вводится ряд понятий, характеризующий потоки с гидравлической и геометрической точек зрения.

Такими понятиями являются: площадь живого сечения потока(или живое сечение потока), расход и средняя скорость.

Площадью живого сечения потока, называют площадь сечения потока, приведенную нормально к направлению линии тока, т.е. перпендикулярно движению струйки жидкости. Живое сечение может быть ограничено твердыми стенками полностью или частично. Если стенки ограничивают поток полностью, то движение жидкости называют напорным; Если же ограничение частичное, то движение называется безнапорным.

Напорное движение характеризуется тем, что гидродинамическое давление в любой точке потока отлично от атмосферного и может быть как больше, так и меньше него. Безнапорное движение характеризуется постоянным давлением на свободной поверхности, обычно равным атмосферному.

Содержание статьи

Расходом потока называется количество жидкости, протекающей через поперечное сечение в единицу времени. Если рассматривать поток жидкости, представляющий собой совокупность большого числа элементарных струек, то очевидно, общий расход жидкости для всего потока в целом представляет собой сумму расходов всех отдельных струек.

Для нахождения этой суммы необходимо знать закон распределения скоростей в сечении потока. Так как во многих случаях движения такой закон неизвестен, в общем случае суммирование становится невозможным. Поэтому в гидродинамике вводится предположение, что все частицы жидкости по всему поперечному сечению потока движутся с одинаковой скоростью. Эту воображаемую фиктивную скорость называют средней скоростью потока υ_ср .

Таким образом уравнение расхода для потока будет

υ_ср – средняя скорость потока

F – площадь сечения потока.

Уравнение неразрывности потока жидкости

Теперь вооружившись основными понятиями перейдем к определению уравнения неразрывности потока.

Отделим сечениями 1-1 и 2-2 некоторый отрезок элементарной струйки. В этот отрезок в единицу времени через сечение 1-1 втекает объем жидкости равный

а через сечение 2-2 из него же вытекает объем, равный

Примем, что жидкость несжимаема и что в ней невозможно образование незаполненных жидкостью пространств – т.е. будем считать, что соблюдается условие сплошности или неразрывности движения.

Учитывая, что форма элементарной струйки с течением времени не изменяется и поперечный приток в струйку или отток из ней отсутствуют, приходим к выводу, что элементарные расходы жидкости, проходящие через сечение 1-1 и 2-2, должны быть одинаковы.

Такие соотношения можно составить для любых двух сечений струйки. Поэтому в более общем виде получаем, что всюду вдоль струйки

Это уравнение называется уравнением неразрывности жидкости – оно является первым основным уравнением гидродинамики. Переходя далее к потоку жидкости в целом получаем, что

т.е. средние скорости в поперечных сечениях потока при неразрывности движения обратно пропорциональны площади этих сечений.

Уравнение неразрывности струи жидкости. Уравнение Бернулли.

Вторым основным уравнением гидродинамики является уравнение Бернулли, устанавливающее взаимосвязь между скоростью и давлением в различных сечениях одной и той же струйки.

При рассмотрении уравнения Бернулли также как и в предыдущем случае ограничимся установившемся медленно изменяющимся движением. Выделим в объеме некоторой жидкости одну элементарную струйку и ограничим её в какой-то определенный момент времени Т сечениями 1-1 и 2-2.

Допустим, что через какой-то промежуток времени ΔТ указанный объем переместится в положение 1’ – 1’ и 2’ – 2’. Тогда применяя к движению этого сечению теорему кинетической энергии, определяем, что приращение кинетической энергии движущейся системы материальных частиц равняется сумме работ всех сил, действующих на систему.

Если всё это записать в виде формулы, то

где W – приращение кинетической энергии = m * υ 2 / 2

ΣA – сумма работ действующих сил = P *ΔS

В этих выражениях
m – масса
υ – скорость материальной точки
P – равнодействующая всех сил, приложенных к точке,
ΔS – проекция перемещения точки на направление силы.

Теперь рассмотрим обе части этого выражения по порядку.

Приращение кинетической энергии ΔW

В нашем случае приращение кинетической энергии определяется как разность значений кинетической энергии в двух положениях перемещающегося объема, т.е. как разность кинетической энергии объема образованного сечениями 1-1’ и объема, образованного сечениями 2 – 2’.

Эти объемы являются результатом перемещения за время ΔТ сечений выделенного участка элементарной струйки.

Вспоминая, что по условию неразрывности расход во всех сечениях элементарной струйки одинаков, а следовательно будет равен

масса в этом случае получается равной

Подставляя все это в выражение для кинетической энергии получаем цепочку

ΔW = m * υ 2 ₂ / 2 — m * υ 2 ₁ / 2 = ρ * q * ΔТ * υ 2 ₂ / 2 — ρ * q * ΔТ * υ 2 ₁ / 2

Работа сил действующих на систему ΣA

Теперь перейдем к рассмотрению работы сил, действующих на рассматриваемый объем жидкости. Работа сил тяжести A_Т равна произведению этой силы на путь, пройденный центром массы движущегося объема жидкости по вертикали.

Для рассматриваемой в нашем примере струйки работа сил тяжести будет равна произведению сил тяжести объема занимаемого сечениями 1-1’ и 2 – 2’ на расстояние Z1 –Z2.

Где Z1 и Z2 – расстояния по вертикали от горизонтальной плоскости, называемой плоскостью сравнения до центров масс объемов 1-1’ и 2 – 2’.

Силы давления А_Д , действующие на объем жидкости складываются из сил давления на его боковую поверхность и на концевые поперечные сечения. Работа сил давления на боковую поверхность равна нулю, так как эти силы за все время движения нормальны к перемещению их точек приложения.

Суммарно работа сил давления будет

Подставляя в начальное уравнение

Полученные выражения для ΔW и ΣA получаем

Разделим обе части этого уравнения на m = ρ*q*ΔТ и перегруппируем слагаемые

Учитывая, что сечения 1-1 и 2-2 взяты нами совершенно произвольным образом, это уравнение возможно распространить на всю струйку. Применив его для любых поперечных сечений, взятых по её длине, и представить в общем виде:

Записанные выше два уравнения представляют собой уравнение Бернулли для элементарной струйки жидкости. Сумма трех слагаемых, входящих в это уравнение, называется удельной энергией жидкости в данном сечении струйки. Различают такие энергии как:
Удельная энергия положения = qz
Удельная энергия давления = p/ ρ
Кинетическая удельная энергия = υ 2 / 2

В соответствии с этим уравнение Бернулли для струйки жидкости можно сформулировать следующим образом: для элементарной струйки идеальной жидкости полная удельная энергия, т.е. сумма удельной энергии положения, удельной энергии давления и кинетической удельной энергии – есть величина постоянная во всех сечениях струйки.

Видео по теме уравнение неразрывности

Полученные в результате многочисленных экспериментов данные из уравнения Бернулли и уравнения неразрывности потока жидкости нашли широкое применение в повседневной жизни.

Уравнение Бернулли широко используется для нахождения скорости истечения жидкости через отверстия.

Уравнение неразрывности обладает широкой универсальностью и справедливо для любой сплошной среды. Принцип уравнения неразрывности используется для формирования сильной и дальнобойной струи воды при тушении пожаров.

Гидродинамика. Уравнение неразрывности движения жидкости.

Уравнение неразрывности потока демонстрирует закон сохранения массы: количество втекающей и вытекающей жидкости неизменно.

Проанализируем сечение 1 с площадью и скоростью движения частиц жидкости обозначим и₁. Элементарный расход для него представлен соотношением:

Далее проанализируем сечение 2 в этой же струйке с площадью сечения и скоростью обозначим и₂. Элементарный расход для него представлен соотношением:

Но согласно характерной особенности элементарной струйки притока и оттока жидкости через ее боковую поверхность не существует; на промежутке 1 — 2, которому свойственны постоянные размеры, отсутствуют пустоты и отсутствуют переуплотнения количества жидкости, протекающей в единицу времени сквозь сечения 1 и 2,будут одинаковыми, тогда:

Уравнение неразрывности для элементарной струйки — элементарный расход жидкости при установившемся движении величина одинаковая для всей элементарной струйки.

Проанализируем трубу с переменным живым сечением. Расход жидкости через трубу для всякого ее сечении постоянен, т.е. Q₁=Q₂= const, делаем вывод:

Значит, когда течение в трубе сплошное и неразрывное, то уравнение неразрывности станет:

Найдем отсюда скорость для выходного сечения:

Обратим внимание, что скорость возрастает обратно пропорционально площади живого сечения потока. Указанная обратная зависимость между скоростью и площадью выступает важным следствием уравнения неразрывности и нашла широкое применение. Так, к примеру, эта особенность используется пожарными при тушении пожара для формирования сильной и дальнобойной струи.

Что произойдет со скорость потока при сужении, когда диаметр напорной трубы d сузиться в два раза?

Площадь живого сечения трубы вычисляем на основе формулы w = πd 2 / 4. В этом случае соотношение площадей в формуле u₂ = u₁ w₁ / w₂ равняться 4.

Следовательно, в ситуации, когда диаметр трубы сужается в два раза — скорость потока возрастет в четыре раза. По аналогии, когда диаметр сузится в три раза — скорость увеличиться в девять раз.

Уравнение неразрывности потока

В. В. Богачев

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

РАБОТЫ НАГНЕТАТЕЛЕЙ

Рецензенты:

Богачев, В. В.

Б Теоретические основы работы нагнетателей : учебное пособие (курс лекций) / В. В. Богачев. – Ставрополь : СевКавГТУ, 2010. – 82 с.

СОДЕРЖАНИЕ

ЛЕКЦИЯ 1. ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕХНИЧЕСКОЙ МЕХАНИКИ ЖИДКОСТЕЙ. ПАРАМЕТРЫ РАБОТЫ НАГНЕТАТЕЛЕЙ. 6

1.1. Уравнение неразрывности потока. 6

1.2. Уравнение движения. 7

1.3. Гидравлические сопротивления. 10

Контрольные вопросы. 12

ЛЕКЦИЯ 2. УРАВНЕНИЕ ЭЙЛЕРА ДЛЯ РАБОТЫ ЛОПАСТНОГО КОЛЕСА 13

2.1. Уравнение Эйлера для работы лопастного колеса. 15

2.2. Характеристики лопастных нагнетателей. 16

Контрольные вопросы. 18

ЛЕКЦИЯ 3. ПОТЕРИ ДАВЛЕНИЯ В НАГНЕТАТЕЛЯХ.

ПОДОБИЕ ЛОПАСТНЫХ НАГНЕТАТЕЛЕЙ. 19

3.1. Потери перед рабочим колесом. 19

3.2. Потери в рабочем колесе. 20

3.3. Потери за рабочим колесом. 21

3.4. Подобие лопастных нагнетателей. 27

3.5. Универсальные характеристики. 29

3.6. Общие характеристики. 31

3.7. Безразмерные (отвлеченные) характеристики. 32

Контрольные вопросы. 33

ЛЕКЦИЯ 4. РАБОТА НАГНЕТАТЕЛЯ В СЕТИ. 34

4.1. Потери давления в сети. 34

4.2. Работа насоса в сети. 37

4.3. Метод наложения характеристик. 38

4.4. Присоединение нагнетателя к сети. 39

4.5. Выходные элементы вентиляционных установок. 41

Контрольные вопросы. 42

ЛЕКЦИЯ 5. СОВМЕСТНАЯ РАБОТА НАГНЕТАТЕЛЕЙ. 43

5.1. Параллельное включение нагнетателей. 43

5.2. Методика построения характеристик. 45

5.3. Последовательное включение нагнетателей. 48

5.4. Нагнетатели с одинаковой характери­стикой. 50

5.5. Нагнетатели с разными характеристи­ками. 50

Контрольные вопросы. 52

ЛЕКЦИЯ 6. ЭКСПЛУАТАЦИОННЫЕ ОСОБЕННОСТИ РАБОТЫ НАГНЕТАТЕЛЕЙ В СЕТЯХ. 53

6.1. Неточность расчета потерь давления в сети. 53

6.2. Отключение и дросселирование сети. 54

6.3. Негерметичность сети. 55

6.4. Изменение температуры. 55

6.5. Перемещение механических примесей. 57

Контрольные вопросы. 59

ЛЕКЦИЯ 7. УСТОЙЧИВОСТЬ РАБОТЫ НАГНЕТАТЕЛЕЙ. 60

7.1. Возникновение неустойчивых режимов работы. 60

7.3. Кавитация. 63

Контрольные вопросы. 67

ЛЕКЦИЯ 8. РЕГУЛИРОВАНИЕ НАГНЕТАТЕЛЕЙ. 68

8.1. Способы регулирования. 68

8.2. Дросселирование. 69

8.3. Регулирование перепуском. 71

8.4. Изменение частоты вращения рабочего колеса. 72

8.5. Регулирование частоты вращения нагнетателя

с по­мощью гидромуфты. 73

8.6. Изменение относительной скорости. 76

8.7. Закручивание потока перед рабочим колесом. 77

8.8. Осевой направляющий аппарат. 78

Контрольные вопросы. 80

СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ. 81

ВВЕДЕНИЕ

ЛЕКЦИЯ 1

ОСНОВНЫЕ СВЕДЕНИЯ ИЗ ТЕХНИЧЕСКОЙ МЕХАНИКИ ЖИДКОСТЕЙ. ПАРАМЕТРЫ РАБОТЫ НАГНЕТАТЕЛЕЙ

Техническая гидроаэромеханика изучает законы движе­ния, относительного покоя и взаимодействия жидкости с твердыми телами, которые либо находятся в ней, либо ее ограничивают. Под жидкостью понимают такую мате­риальную среду, медленная деформация которой при по­стоянном объеме возможна под действием ничтожно ма­лых сил. Жидкости делятся на два класса: малосжимаемые – капельные и сжимаемые – газы. При движении газов со скоростями, значительно меньшими скорости звука, сжимаемостью газа можно пренебречь. В этом случае при исследовании движения газов применяют уравнения движения капельных жидкостей. Техническая механика жидкости базируется на ос­новных законах сохранения массы, энергии и импульса, которые широко применяются в технике.

Уравнение неразрывности потока

Рассмотрим уста­новившееся движение жидкости в канале произвольного сечения (рис. 1.1).

Пусть поток движется со скоростью с от сечения 1 – 1 к сечению 2 – 2.В соответствии с зако­ном сохранения массы вещества та масса жидкости, ко­торая находится между сечениями 1 – 2 и 2 – 2, для рас­сматриваемого случая движения должна быть постоян­ной. Это означает, что масса жидкости, прошедшая че­рез живое сечение канала площадью ω₁ будет равна массе жидкости, прошедшей через живое сечение кана­ла площадью ω₂, т. е.

(1.1)

где ρ₁ и ρ₂ – плотность жидкости, проходящей через сечение 1 – 1и 2 – 2 соответственно.

Выражение (1.1), являясь следствием закона сохра­нения массы, называется уравнением неразрывности по­тока жидкости. Из уравнения неразрывности потока, часто записываемого в виде

(1.2)

следует, что, если предположить существование внутри установившегося потока жидких струек, для каждой из которых должно выполняться условие (1.2), то они нигде не могут закончиться. Эти струйки либо должны простираться от одной границы рассматриваемого про­странства до другой, либо замыкаться. В тех случаях, когда несжимаемые (капельные) жидкости или газы движутся под действием относительно малых перепадов давления и весь поток рассматривается как одна жидкая струйка, произведение ωc = Q называют объемным рас­ходом потока, а произведение ρωc = М – массовым рас­ходом.

Уравнение движения

Известно, что основными си­лами, действующими в движущейся жидкости, являют­ся массовые и поверхностные. Если канал, в котором движется жидкость, является неподвижным, то единст­венной массовой силой, действующей в жидкости, будет вес. К поверхностным силам относится силы гидродина­мического давления и силы трения.

Количественной мерой различных форм движения материи служит понятие, называемое в физике энер­гией. Если тело движется, то оно обладает энергией; если тело обладает энергией, оно может совершить ра­боту, которая в дальнейшем (в соответствии с принци­пами сохранения энергии) может перейти в другую фор­му энергии (например, в тепловую).

Рассмотрим установившееся движение вязкой жидко­сти с учетом ее сжимаемости. Как известно, при движе­нии сжимаемых жидкостей работа сил трения оказыва­ет двоякое действие: с одной стороны, являясь реактив­ной силой, она тормозит поток, действуя в противопо­ложном движению направлении; с другой стороны, рабо­та сил трения, целиком превращаясь в теплоту, возвра­щается в поток в виде тепловой энергии, которая может расходоваться на расширение жидкости и, следователь­но, на ускорение ее движения.

Выделим некоторый объем в трубке тока движущей­ся жидкости и ограничим его сечениями 1 – 1 и 2 – 2(рис. 1.2).

Рассматривая установившееся движение, за­пишем для этого объема уравнение сохранения энергии в следующей формулировке: работа внешних сил плюс подведенная теплота расходуются на изменение механи­ческой и внутренней энергии рабочего тела. Как извест­но, внешними силами, действующими при перемещении жидкости от сечения 1 – 1 к сечению 2 – 2,являются силы давления и силы трения. Пусть за некоторый про­межуток времени под действием сил давления произо­шло перемещение объема жидкости, заключенного меж­ду сечениями 1 – 1 и 2 – 2, в сечения 1’ – 1’ и 2′ – 2′.Это означает, что вблизи сечения 1 – 1(см. рис. 1.2) исчез­нет элемент массы

а около сечения 2 – 2 появится равный ему элемент массы

Спроектируем все силы на направление движения массы жидкости. Силы гидродинамического давления, действующие на боковую поверхность выделенного объе­ма, составляющих в направлении движения не дадут, и их работа по перемещению массы жидкости равна нулю. Таким образом, суммарная работа сил давления, под действием которых произошло перемещение жидкоcти из сечения 1 – 1 в сечение 2 – 2, определится выражением:

(1.3)

Обозначим удельную работу сил трения, возникаю­щую в потоке движущейся жидкости при перемещении ее из сечения 1 – 1 в сечение 2 – 2,ΔR. Таким образом, суммарная удельная работа внешних сил, совершаемая при перемещении потока жидкости из сечения 1 – 1 в се­чение 2 – 2,с учетом направления действия этих сил за­пишется в виде p₁V₁ – p₂V₂ – ΔR.

Вследствие работы вязких сил возможный приток теплоты в трубку тока между сечениями 1 – 1 и 2 – 2 будет равен MΔq, где Δq – количество теплоты, полу­ченное каждой единицей массы жидкости, прошедшей путь между этими сечениями. Таким образом, Δq – удельное количество теплоты, поступающей в массу жидкости между сечениями 1 – 1 и 2 – 2.

В соответствии с законом сохранения энергии удель­ные работа внешних сил и подведенная теплота долж­ны привести к изменению удельных механической и внутренней энергий потока жидкости. Удельную внут­реннюю энергию массы жидкости обозначим через U.

Масса жидкости, находящейся между сечениями 1 – 1 и 2 – 2, остается постоянной, поэтому изменение удель­ной энергии при перемещении жидкости из сечения 1 – 1 в сечение 2 – 2определится как разность удельных энер­гий элементов массы dm₂ и dm₁. Таким образом, закон сохранения удельной энергии для выделенного элемен­та трубки тока может быть записан в виде

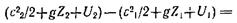(1.4)

Полученное выражение (1.4) часто используется в дифференциальной форме:

Уравнение сохранения энергии (1.5) может быть до­полнено уравнением, вытекающим из первого начала термодинамики, согласно которому подведенная к си­стеме теплота увеличивает ее внутреннюю энергию и со­вершает работу расширения, т. е.

Подставляя выражение (1.6) в уравнение (1.5) и интегрируя имеем выражение

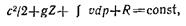(1.7)

представляющее собой уравнение Д. Бернулли, учиты­вающее как сжимаемость жидкости, так и работу сил трения. Каждый член уравнения (1.7) определяет удель­ную энергию или удельную работу.