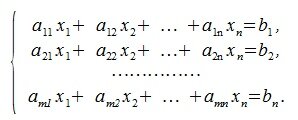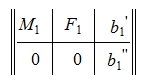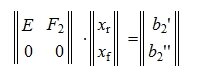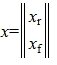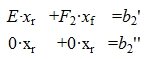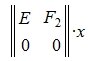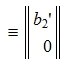Какая система линейных уравнений называется неоднородной

Фундаментальная система решений СЛАУ

Вы будете перенаправлены на Автор24

Системой линейных уравнений называется система вида: $\begin a_ <11>\cdot x_1 +. + a_ <1n>\cdot x_n = b_1 \\ . \\ a_ \cdot x_1 + a_ \cdot x_n = b_m \end$

Здесь каждая буква относится к своей группе обозначений, $x_1. x_n$ — это неизвестные числа или переменные, подлежащие поиску, $a_11. a_$ — множители, содержащиеся при неизвестных, $b_1. b_m$ — свободные члены таблицы из чисел, получаемой на основе приведённой СЛАУ.

В компактной форме СЛАУ принято записывать в виде формулы вида $A \cdot X = B$. В этой формуле под большой буквой $A$ подразумевается матрица множителей при неизвестных системы, а буквами $X$ и $B$ обозначены вектор-столбец неизвестных системы и свободных членов.

Матрица $A$ называется основной матрицей системы, вот как она будет выглядеть:

$A = \begin a_ <11>& … & a_ <1n>\\ \vdots & … & \vdots \\ a_ & … & a_ \end$, $b=\begin b_1 \\ \vdots \\ b_m \end$

Если через длинную черту после матрицы множителей при неизвестных записан столбец свободных членов, то матрицу называют расширенной матрицей системы.

Необходимая терминология

Решением системы называют такие $n$ значений неизвестных $x_1=c_1, x_2=c_2…x_n-c_n$, что при их использовании все её уравнения становятся верными соблюдающимися равенствами. Найденное решение системы можно записать в виде таблицы неизвестных одним столбцом:

$C= \begin c_1 \\ c_2 \\ \vdots \\ c_n \end$.

В зависимости от количеств групп переменных, подходящих для соблюдения всей системы, различают совместные и несовместные СЛАУ. Объединённая в систему группа равенств называется совместной, если она имеет хотя бы одно решение и несовместной, если она не имеет решений.

Готовые работы на аналогичную тему

Среди первого типа существуют определённые СЛАУ, имеющие только одно решение и неопределённые, под такие подпадают все, которые можно решить с получением больше одного ответа.

Однородные и неоднородные системы линейных уравнений

Система линейных уравнений называется однородной, если все её свободные члены равны нулю. Если в системе хотя бы один из свободных членов ненулевой, то она называется неоднородной, другие же СЛАУ с нулевым $B$ наоборот однородны.

Однородные системы совместны, так как $x_1=x_2=. x_n=0$ будет решением для систем, имеющих особенность в виде нулевого столбца $B$. Иначе такая группа ответов называется нулевым или тривиальным способом решения.

Нетривиальными же называются ответы на СЛАУ, детерминант матрицы которой не $0$. В группе ответов таких систем хотя бы одно из неизвестных подходит под $x_i$ ≠ $0$. Для поиска детерминанта можно воспользоваться $LU$ разложениями, гаусовым методом или его модификацией в виде способа Жордана-Гаусса.

Общее, частное и фундаментальное решения

Частным решением системы называется индивидуальное записанное в одну строчку, тогда как общее $X_o$ записывается через свободные переменные в одну строчку, оно представляет собой некое множество чисел, подходящих под данные условия. Общее $X_o$ включает в себя все индивидуальные.

Фундаментальной же системой решений (ФСР) называется совокупность $(n-r)$ векторов, являющихся линейно независимыми векторами системы. Здесь $r$ — это ранг исследуемой матрицы, согласно теореме Капелли, он равен количеству её основных неизвестных. Найти его можно путём разрешённых преобразований над изучаемым объектом, в частности, можно использовать метод Гаусса или другие.

Фундаментальная система решений частенько представлена как сумма всех возможных решений:

Здесь $С_1, C_2. C_$ — некоторые постоянные.

Приведена пример, в котором все свободные члены ненулевые:

$\begin x_1 – x_2 + x_3-x_4=4 \\ x_1+x_2+2x_3+3x_4=8 \\ 2x_1+4x_2+5x_3+10x_4=20 \\ 2x_1-4x_2+x_3-6x_4=4\\ \end$.

Ранг всех матриц соответсвует двойке, рассчитаем базисный минор:

Избавимся от двух нижних равенств из примера и получим:

$\begin x_1 – x_2=4-c_3+c_4 \\ x_1+x_2=8-2c_3-3c_4 \\ \end$

Общим решением системы будет строчка $(6-\frac<3><2>c_3-c_4; 2-\frac<1><2>c_3-2c_4;c_3; c_4)$.

Теперь посмотрим, что буде в случае с нулевым столбцом за чертой:

$\begin x_1 – x_2 + x_3-x_4=0 \\ x_1+x_2+2x_3+3x_4=0 \\ 2x_1+4x_2+5x_3+10x_4=0 \\ 2x_1-4x_2+x_3-6x_4=0 \end$.

Ранг также соответствует двойке, а её решениями будут

$c_1=-\frac<3> <2>c_3-c_4; c_2=-\frac<1><2>c_3-2c_4$. Константы же $c_3$ и $c_4$ выберем любые, например, возьмём их равными $c_3=0;c_4=1$.

Итак, используя приведённые выше значения $c_3=0;c_4=1$:

Фундаментальное решение системы можно записать так:

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 17 04 2021

Какая система линейных уравнений называется неоднородной

Пусть задана неоднородная система линейных алгебраических уравнений размерности m × n .

Матрица называется расширенной матрицей системы, если наряду с коэффициентами при неизвестных, она содержит столбец свободных членов. Следовательно, размерность равна m × (n+1) .

Исследование любой системы линейных алгебраических уравнений начинается с преобразования ее расширенной матрицы методом Гаусса , который основан на следующих элементарных преобразованиях:

– перестановка строк матрицы;

– умножение строк матрицы на действительное отличное от руля число;

– поэлементное сложение строк матрицы;

– вычеркивание нулевой строки;

– транспонирование матрицы (в этом случае преобразования производятся по столбцам).

Элементарные преобразования приводят первоначальную систему к системе, ей эквивалентной. Системы называются эквивалентными, если они имеют одно и то же множество решений.

Рангом матрицы называется наивысший порядок отличных от нуля ее миноров. Элементарные преобразования ранга матрицы не меняют.

На вопрос о наличии решений у неоднородной системы линейных уравнений отвечает следующая теорема.

Теорема 1.3 (теорема Кронекера-Капелли). Неоднородная система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг расширенной матрицы системы равен рангу ее главной матрицы, то есть

Обозначим количество строк, оставшихся в матрице после метода Гаусса, через r (соответственно, в системе остается r уравнений). Эти строки матрицы называются базисными.

Если r = n , то система имеет единственное решение (является совместной определенной), ее матрица элементарными преобразованиями приводится к треугольному виду. Такую систему можно решить также методом Крамера и с помощью обратной матрицы .

Если r n (количество переменных в системе больше количеств а уравнений), матрица элементарными преобразованиями приводится к ступенчатому виду. Такая система имеет множество решений и является совместной неопределенной. В данном случае для нахождения решений системы необходимо выполнить ряд операций.

1. Оставить в левых частях уравнений системы r неизвестных (базисные переменные), остальные n — r неизвестных перенести в правые части (свободные переменные). После разделения переменных на базисные и свободные система принимает вид:

2. Из коэффициентов при базисных переменных составить минор (базисный минор), который должен быть отличен от нуля.

3. Если базисный минор системы (1.10) равен нулю, то одну из базисных переменных следует заменить на свободную; полученный базисный минор снова проверить на отличие от нуля.

4. Применяя формулы (1.6) метода Крамера, считая правые части уравнений их свободными членами, найти выражение базисных переменных через свободные в общем виде. Полученный при этом упорядоченный набор переменных системы является ее общим решением.

5. Придавая свободным переменным в (1.10) произвольные значения, вычислить соответствующие значения базисных переменных. Получаемый при этом упорядоченный набор значений всех переменных называется частным решением системы, соответствующим данным значениям свободных переменных. Система имеет бесконечное множество частных решений.

6. Получить базисное решение системы – частное решение, получаемое при нулевых значениях свободных переменных.

Заметим, что количество базисных наборов переменных системы (1.10) равно числу сочетаний из n элементов по r элементов C_n r . Так как каждому базисному набору переменных соответствует свое базисное решение, следовательно, количество базисных решений у системы также равно C_n r .

Пусть строки матрицы обозначены соответственно l ₁ ; l ₂ ;…; l_n . Строка l называется линейной комбинацией строк l ₁ ; l ₂ ;…; l_n матрицы, если она равна сумме произведений этих строк на произвольные действительные числа, то есть , .

Однородная система уравнений всегда совместна, так как имеет хотя бы одно – нулевое (тривиальное) решение. Для того чтобы однородная система n линейных уравнений с n переменными имела ненулевые решения, необходимо и достаточно, чтобы ее главный определитель ∆ был равен нулю. Это означает, что ранг r ее главной матрицы меньше числа n неизвестных ( r n ) . В этом случае исследование однородной системы уравнений на общее и частные решения проводится аналогично исследованию неоднородной системы. Решения однородной системы уравнений обладают важным свойством: если известны два различных решения однородной системы линейных алгебраических уравнений, то их линейная комбинация также является решением этой системы. Нетрудно убедиться в справедливости следующей теоремы.

Теорема 1.4. Общее решение неоднородной системы уравнений представляет собой сумму общего решения соответствующей однородной системы и некоторого частного решения неоднородной системы уравнений

Пример 1.7. Исследовать заданную систему уравнений и найти одно частное решение:

Решение. Выпишем расширенную матрицу системы и применим к ней элементарные преобразования:

Так как r ( A ) =2 и , то по теореме 1.3 (Кронекера-Капелли) заданная система линейных алгебраических уравнений совместна. Количество переменных n =2 , т.е. r n , значит, система является неопределённой. Количество базисных наборов переменных системы равно . Следовательно, базисными могут быть 6 комплектов переменных: < x ₁ ; x ₂ >, < x ₁ ; x ₃ >, < x ₁ ; x ₄ >, < x ₂ ; x ₃ >, < x ₂ ; x ₄ >, < x ₃ ; x ₄ > . Рассмотрим один из них < x ₁ ; x ₂ > . Тогда систему, полученную в результате метода Гаусса, можно переписать в виде . Главный определитель . С помощью метода Крамера ищем общее решение системы.

По формулам (1.6) имеем

Данное выражение базисных переменных через свободные представляет собой общее решение системы:

При конкретных значениях свободных переменных из общего решения получаем частное решение системы. Например, частное решение соответствует значениям свободных переменных x ₃ = x ₄ = 17 . При x₃=0 x₄=0 получаем базисное решение системы

Система линейных уравнений. Общее решение

Система линейных уравнений (СЛУ) может быть записана в виде

где m, n натуральные числа, a_ij (i= 1,2, . m, j= 1,2. n) называются коэффициентами, b_i (i= 1,2. m) называются свободными членами, x_i (i= 1,2. n) называются неизвестными.

Систему линейных уравнений (1) можно записать в виде

где A матрица порядка m×n , x — вектор порядка n (x∈R n ), b — вектор порядка m (b ∈R m ).

Решением системы (2) называется выбор такого вектора x’, что выполнено равенство

Если система линейных уравнений имеет хотя бы одно решение, то СЛУ называется совместным.

Если СЛУ не имеет решения, то СЛУ называется несовместным.

Если СЛУ имеет единственное решение, то СЛУ называется определенным.

Если СЛУ имеет более одного решения, то СЛУ называется неопределенным.

Система линейных уравнений (2) называется неоднородной cистемой линейных уравнений, если b≠0.

Система линейных уравнений (2) называется однородной cистемой линейных уравнений, если b=0.

Нахождение общего решения системы линейных уравнений

Общее решение системы линейных уравнений (1)((или (2))− это множество всех решений этой системы.

Пусть A m×n — матрица rankA=r. В общем случае можем предположить что r .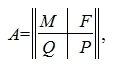

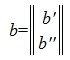
Применяя метод исключения Гаусса для системы (3), получим:

где M₁ верхняя треугольная матрица, 0 — нулевые матрицы соответствующих порядков. Далее, применяя обратный ход исключения Гаусса, и, далее, разделив элементы каждой строки на ведущий элемент этой строки (если ведущий элемент существует) получим:

где E — единичная матрица порядка r×r.

Запишем (5) в виде системы линейных уравнений:

где

Решим систему линейных уравнений (6). Для этого перезапишем в следующем виде:

Из второго уравнения системы (7) следует, что для совместности системы (6) и, следовательно, (2) (или (1)) должно выполняться условие b₂»≡ 0. Если система совместна, то решаем первое уравнение системы (7) относительно вектора x_r:

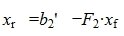(8)

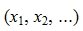
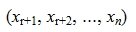
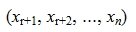
Таким образом первые r координаты вектора x выражены через остальные координаты . — свободные координаты, т.е. могут принимать любые значения.

Найдем, далее, множество всех векторов x, удовлетворяющих уравнению (6) и, следовательно, (2)( или (1)).

Рассмотрим множество всех векторов х, удовлетворяющих условию

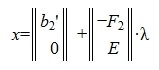(9)

где λ — произвольный вектор-столбец длины n-r.

Подставляя (9) в (6) получим:

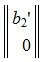
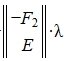
Следовательно (9) является решением системы (6) и, следовательно, (2)(или (1)). Отметим что вектор является частным решением неоднородной системы линейных уравнений Ax=b, а является общим решением однородной системы линейных уравнений Ax=0;

Нахождение общего решения системы линейных уравнений с помощью псевдообратной матрицы

Обозначим через R(A) пространство столбцов матрицы A, т.е.

1. Пусть A n×n матрица и rank(A)=n. Тогда существует обратная к A матрица A -1 , и следовательно единственное решение СЛУ (2) примет вид:

Действительно, подставляя (3) в (2) имеем:

2. Пусть A m×n − матрица, rank(A)=r.